Implementasi FFT Integer FPGA

Halo semuanya!

Suatu kali, pelanggan bertanya kepada saya apakah saya memiliki FFT integer dalam proyek saya, yang saya selalu jawab bahwa ini sudah dilakukan oleh orang lain dalam bentuk siap pakai, meskipun melengkung, tetapi core IP gratis (Altera / Xilinx) - ambil dan gunakan. Namun, core ini tidak optimal , memiliki seperangkat "fitur" dan memerlukan penyempurnaan lebih lanjut. Dalam hubungan ini, setelah pergi pada liburan terencana yang lain, yang saya tidak ingin menghabiskan biasa-biasa saja, saya mulai menerapkan kernel yang dapat dikonfigurasi dari integer FFT.


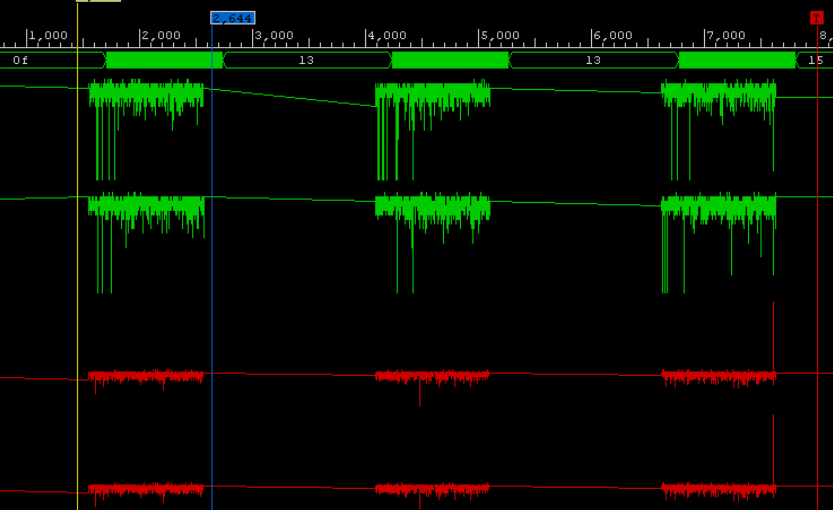_{KDPV (proses debugging data error overflow)}

Dalam artikel ini saya ingin memberi tahu Anda apa metode dan cara operasi matematika direalisasikan ketika menghitung transformasi Fourier cepat dalam format integer pada kristal FPGA modern. Dasar dari setiap FFT adalah simpul yang disebut "kupu-kupu". Kupu-kupu mengimplementasikan operasi matematika - penambahan, perkalian dan pengurangan. Ini adalah tentang implementasi "kupu-kupu" dan simpul-simpulnya yang sudah selesai yang akan menjadi cerita pertama. Berdasarkan keluarga Xilinx FPGA modern - ini adalah seri Ultrascale dan Ultrascale +, serta seri 6 yang lebih lama (Virtex) dan 7- (Artix, Kintex, Virtex) terpengaruh. Seri lama dalam proyek-proyek modern tidak menarik di 2018. Tujuan artikel ini adalah untuk mengungkapkan fitur-fitur dari implementasi kernel khusus pemrosesan sinyal digital menggunakan contoh FFT.

Pendahuluan

Bukan rahasia bagi siapa pun bahwa algoritma untuk mengambil FFT tertanam kuat dalam kehidupan insinyur pemrosesan sinyal digital, dan oleh karena itu alat ini selalu dibutuhkan. Pabrikan FPGA terkemuka seperti Altera / Xilinx sudah memiliki core FFT / IFFT yang dapat dikonfigurasi dengan fleksibel, tetapi mereka memiliki sejumlah keterbatasan dan fitur, dan oleh karena itu saya harus menggunakan pengalaman saya sendiri lebih dari sekali. Jadi kali ini saya harus mengimplementasikan FFT dalam format integer sesuai dengan skema Radix-2 pada FPGA. Dalam artikel terakhir saya, saya sudah melakukan FFT dalam format floating point, dan dari sana Anda tahu bahwa algoritma dengan paralelisme ganda digunakan untuk mengimplementasikan FFT, yaitu, inti dapat memproses dua sampel kompleks pada frekuensi yang sama . Ini adalah fitur FFT utama yang tidak tersedia di kernel siap pakai Xilinx FFT.

Contoh: diperlukan untuk mengembangkan simpul FFT yang melakukan operasi kontinu dari aliran input bilangan kompleks pada frekuensi 800 MHz. Inti dari Xilinx tidak akan melakukan ini (frekuensi clock pemrosesan yang dapat dicapai dalam FPGA modern adalah dari urutan 300-400 MHz), atau itu akan memerlukan menipiskan aliran input entah bagaimana. Inti kustom memungkinkan Anda untuk mencatat dua sampel input pada frekuensi 400 MHz tanpa intervensi sebelumnya, alih-alih sampel tunggal pada 800 MHz. Kekurangan lain dari inti Filin Xilinx adalah ketidakmampuan untuk menerima aliran input dalam urutan bit-reverse . Dalam hubungan ini, sumber daya memori chip besar FPGA dihabiskan untuk mengatur ulang data dalam urutan normal. Untuk tugas konvolusi sinyal yang cepat, ketika dua node FFT berdiri di belakang satu sama lain, ini bisa menjadi momen kritis, yaitu, tugas itu tidak akan terletak pada chip FPGA yang dipilih. Inti FFT khusus memungkinkan Anda menerima data dalam urutan normal pada input, dan mengeluarkannya dalam mode bit-reverse, sedangkan inti dari FFT terbalik - sebaliknya, menerima data dalam urutan bit-reverse, dan mengeluarkannya dalam mode normal. Dua buffer untuk permutasi data disimpan sekaligus !!!

Karena sebagian besar materi dalam artikel ini bisa tumpang tindih dengan yang sebelumnya , saya memutuskan untuk fokus pada topik operasi matematika dalam format integer pada FPGA untuk implementasi FFT.

Parameter kernel FFT

• NFFT - jumlah kupu-kupu (panjang FFT),
• DATA_WIDTH - kedalaman bit data input (4-32),
• TWDL_WIDTH - kedalaman bit dari faktor belok (8-27).
• SERIES - mendefinisikan keluarga FPGA di mana FFT diimplementasikan ("BARU" - Ultrascale, "LAMA" - 6/7 seri Xilinx FPGA).

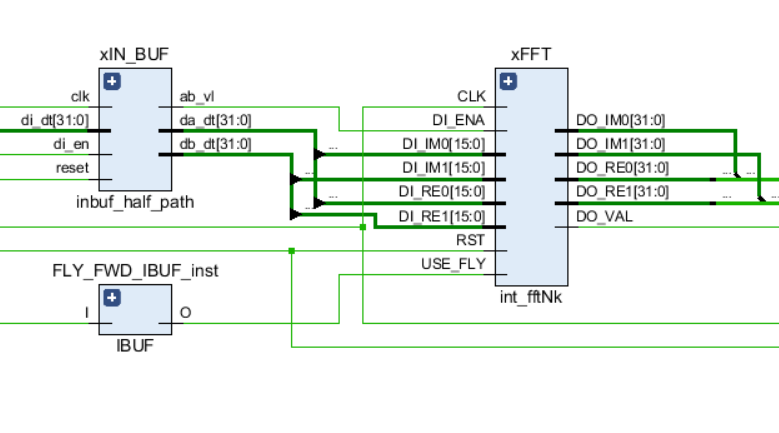
Seperti tautan lainnya di sirkuit, FFT memiliki port kontrol input - sinyal jam dan reset, serta port data input dan output. Selain itu, sinyal USE_FLY digunakan dalam kernel, yang memungkinkan Anda untuk mematikan kupu-kupu FFT secara dinamis untuk proses debugging atau untuk melihat aliran input asli.

Tabel di bawah ini menunjukkan jumlah sumber daya FPGA yang digunakan, tergantung pada panjang NFFT FFT untuk DATA_WIDTH = 16 dan dua bit TWDL_WIDTH = 16 dan 24 bit.



Inti pada NFFT = 64K stabil pada frekuensi pemrosesan FREQ = 375 MHz pada kristal Kintex-7 (410T).

Struktur proyek

Grafik skematis dari simpul FFT ditunjukkan pada gambar berikut:


Untuk kenyamanan memahami fitur komponen tertentu, saya akan memberikan daftar file proyek dan deskripsi singkatnya dalam urutan hierarkis:

• Kernel FFT:
  
  • int_fftNk - Node FFT, sirkuit Radix-2, penipisan frekuensi (DIF), aliran input normal, aliran output sedikit terbalik.
  • int_ifftNk - Node OBPF , sirkuit Radix-2, penipisan waktu (DIT), aliran input sedikit terbalik, aliran keluaran normal.
• Kupu-kupu:
  
  
  • int_dif2_fly - butterfly Radix-2, penipisan frekuensi,
  • int_dit2_fly - butterfly Radix-2, penipisan waktu,
• Pengganda Kompleks:
  
  
  • int_cmult_dsp48 - pengganda yang dapat dikonfigurasi secara umum, termasuk:
  • int_cmult18x25_dsp48 - pengali untuk kedalaman bit kecil dari data dan faktor rotasi,
  • int_cmult_dbl18_dsp48 - pengganda berlipat ganda, lebar bit dari faktor belok hingga 18 bit,
  • int_cmult_dbl35_dsp48 - pengganda dua kali lipat, lebar bit dari faktor-faktor berputar hingga 25 * bit,
  • int_cmult_trpl18_dsp48 - pengali tiga, kapasitas faktor balik hingga 18 bit,
  • int_cmult_trpl52_dsp48 - pengali tiga, kapasitas faktor berputar hingga 25 * bit,
• Pengganda:
  
  
  • mlt42x18_dsp48e1 - pengganda dengan bit operan hingga 42 dan 18 bit berdasarkan DSP48E1,
  • mlt59x18_dsp48e1 - pengganda dengan bit operan hingga 59 dan 18 bit berdasarkan pada DSP48E1,
  • mlt35x25_dsp48e1 - pengganda dengan bit operan hingga 35 dan 25 bit berdasarkan DSP48E1,
  • mlt52x25_dsp48e1 - pengganda dengan bit operan hingga 52 dan 25 bit berdasarkan DSP48E1,
  • mlt44x18_dsp48e2 - pengganda dengan bit operan hingga 44 dan 18 bit berdasarkan DSP48E2,
  • mlt61x18_dsp48e2 - pengganda dengan bit operan hingga 61 dan 18 bit berdasarkan pada DSP48E2,
  • mlt35x27_dsp48e2 - pengganda dengan bit operan hingga 35 dan 27 bit berdasarkan pada DSP48E2,
  • mlt52x27_dsp48e2 adalah pengganda dengan bit operan hingga 52 dan 27 bit berdasarkan pada DSP48E2.
• Penghancur:
  
  
  • int_addsub_dsp48 - penambah universal, operan bit hingga 96 bit.
• Garis keterlambatan:
  
  
  • int_delay_line - garis dasar penundaan, memberikan permutasi data antara kupu-kupu,
  • int_align_fft - penyelarasan data input dan faktor balik pada input kupu-kupu FFT,
  • int_align_fft - penyelarasan data input dan faktor balik pada input kupu-kupu OBPF ,
• Rotating Factor:
  
  
  • rom_twiddle_int - generator faktor rotari, dari panjang tertentu FFT mempertimbangkan koefisien berdasarkan sel FPGA DSP,
  • row_twiddle_tay - generator faktor rotari menggunakan seri Taylor (NFFT> 2K) **.
• Buffer data:
  
  
  • inbuf_half_path - buffer input, menerima aliran dalam mode normal dan menghasilkan dua urutan sampel yang digeser setengah panjang FFT ***,
  • outbuf_half_path - buffer output, mengumpulkan dua urutan dan menghasilkan satu kontinu yang sama dengan panjang FFT,
  • iobuf_flow_int2 - buffer berfungsi dalam dua mode: ia menerima aliran dalam mode Interleave-2 dan menghasilkan dua urutan FFT yang digeser setengah panjangnya. Atau sebaliknya, tergantung pada opsi BITREV.
  • int_bitrev_ord adalah konverter data sederhana dari urutan alami ke bit-mundur.

* - untuk DSP48E1: 25 bit, untuk DSP48E2 - 27 bit.
** - dari tahap tertentu FFT, sejumlah memori blok dapat digunakan untuk menyimpan koefisien rotasi, dan koefisien antara dapat dihitung dengan menggunakan node DSP48 menggunakan rumus Taylor dengan turunan pertama. Karena fakta bahwa sumber daya memori lebih penting untuk FFT, Anda dapat dengan aman mengorbankan unit komputasi demi memori.
*** - garis buffer dan delay input - memberikan kontribusi signifikan terhadap jumlah sumber daya memori FPGA yang diduduki

Kupu-kupu

Setiap orang yang setidaknya pernah mengalami algoritma transformasi Fourier cepat tahu bahwa algoritma ini didasarkan pada operasi dasar - "kupu-kupu". Ini mengubah input stream dengan mengalikan input dengan faktor twiddle. Ada dua skema konversi klasik untuk FFT - penipisan dalam frekuensi (DIF, penipisan-dalam-frekuensi) dan penipisan dalam waktu (DIT, penipisan-dalam-waktu). Algoritme DIT ditandai dengan membagi urutan input menjadi dua urutan durasi setengah, dan algoritma DIF menjadi dua urutan sampel genap dan ganjil dari durasi NFFT. Selain itu, algoritma ini berbeda dalam operasi matematika untuk operasi kupu-kupu.



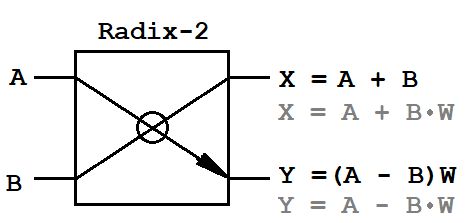A, B - pasang input sampel kompleks,
X, Y - pasangan keluaran sampel kompleks,
Faktor balik W - kompleks.

Karena data input adalah jumlah yang kompleks, kupu-kupu memerlukan satu pengali kompleks (4 operasi perkalian dan 2 operasi penambahan) dan dua penambahan kompleks (4 operasi penambahan). Ini adalah seluruh dasar matematika yang harus diimplementasikan pada FPGA.

Pengganda

Perlu dicatat bahwa semua operasi matematika pada FPGA sering dilakukan dalam kode tambahan (komplemen 2's). Pengganda FPGA dapat diimplementasikan dalam dua cara - pada logika menggunakan pemicu dan tabel LUT, atau pada unit perhitungan DSP48 khusus, yang telah lama dan tegas dimasukkan dalam semua FPGA modern. Pada blok logis, penggandaan diimplementasikan menggunakan algoritma Booth atau modifikasinya, membutuhkan sumber daya logis yang layak dan tidak selalu memenuhi batasan waktu pada frekuensi pemrosesan data yang tinggi. Dalam hal ini, pengganda FPGA dalam proyek modern hampir selalu dirancang berdasarkan node DSP48 dan hanya sesekali pada logika. Node DSP48 adalah sel jadi kompleks yang mengimplementasikan fungsi matematika dan logis. Operasi dasar: penggandaan, penambahan, pengurangan, akumulasi, penghitung, operasi logis (XOR, NAND, AND, OR, NOR), kuadrat, perbandingan angka, shift, dll. Gambar berikut menunjukkan sel DSP48E2 untuk keluarga Xilinx Ultrascale + FPGA.



Melalui konfigurasi port input yang sederhana, operasi perhitungan dalam node dan penundaan pengaturan di dalam node, Anda dapat membuat data matematika berkecepatan tinggi.
Perhatikan bahwa semua vendor FPGA teratas dalam lingkungan pengembangan memiliki core IP standar dan gratis untuk menghitung fungsi matematika berdasarkan pada simpul DSP48. Mereka memungkinkan Anda untuk menghitung fungsi matematika primitif dan mengatur berbagai penundaan pada input dan output dari node. Untuk Xilinx, ini adalah IP-Core "pengganda" (ver. 12.0, 2018), yang memungkinkan Anda untuk mengonfigurasikan pengganda ke kedalaman bit data input mulai dari 2 hingga 64 bit. Selain itu, Anda dapat menentukan bagaimana pengali diimplementasikan - pada sumber daya logis atau pada primitif DSP48 bawaan.

Perkirakan berapa banyak logika pengali "makan" dengan kedalaman bit dari input data pada port A dan B = 64 bit. Jika Anda menggunakan node DSP48, maka mereka hanya perlu 16.



Keterbatasan utama pada sel DSP48 adalah kedalaman bit dari data input. Node DSP48E1, yang merupakan sel dasar dari seri FPGA Xilinx 6 dan 7, lebar port input untuk perkalian: "A" - 25 bit, "B" - 18 bit, Oleh karena itu, hasil penggandaan adalah angka 43-bit. Untuk keluarga Xilinx Ultrascale dan Ultrascale + FPGA, node telah mengalami beberapa perubahan, khususnya, kapasitas port pertama meningkat dua bit: "A" - 27 bit, "B" - 18 - bit. Selain itu, simpul itu sendiri disebut DSP48E2.

Agar tidak terikat dengan keluarga tertentu dan chip FPGA, untuk memastikan "kemurnian kode sumber", dan untuk memperhitungkan semua kedalaman bit yang mungkin dari data input, diputuskan untuk merancang set pengganda sendiri. Ini akan memungkinkan implementasi pengganda kompleks yang paling efisien untuk kupu-kupu FFT, yaitu, pengganda dan pengurang-penambah berdasarkan blok DSP48. Input pertama dari pengali adalah input data, input kedua dari pengali adalah faktor-faktor yang berputar (sinyal harmonik dari memori). Seperangkat pengganda diimplementasikan menggunakan pustaka UNISIM bawaan, yang darinya perlu untuk menghubungkan primitif DSP48E1 dan DSP48E2 untuk digunakan lebih lanjut dalam proyek. Satu set pengganda disajikan dalam tabel. Perlu dicatat bahwa:

• Pengoperasian angka yang berlipat ganda mengarah pada peningkatan kapasitas produk sebagai jumlah dari kapasitas operan.
• Setiap pengganda 25x18 dan 27x18 digandakan, pada kenyataannya - ini adalah salah satu komponen untuk keluarga yang berbeda.
• Semakin besar tahap paralelisme operasi, semakin besar keterlambatan dalam komputasi dan semakin besar jumlah sumber daya yang digunakan.
• Dengan kedalaman bit yang lebih rendah pada input "B", pengganda dengan kedalaman bit yang lebih tinggi pada input lain dapat diimplementasikan.
• Keterbatasan utama dalam meningkatkan kedalaman bit diperkenalkan oleh port "B" (port sebenarnya dari DSP48 primitif) dan register geser internal sebesar 17-bit.

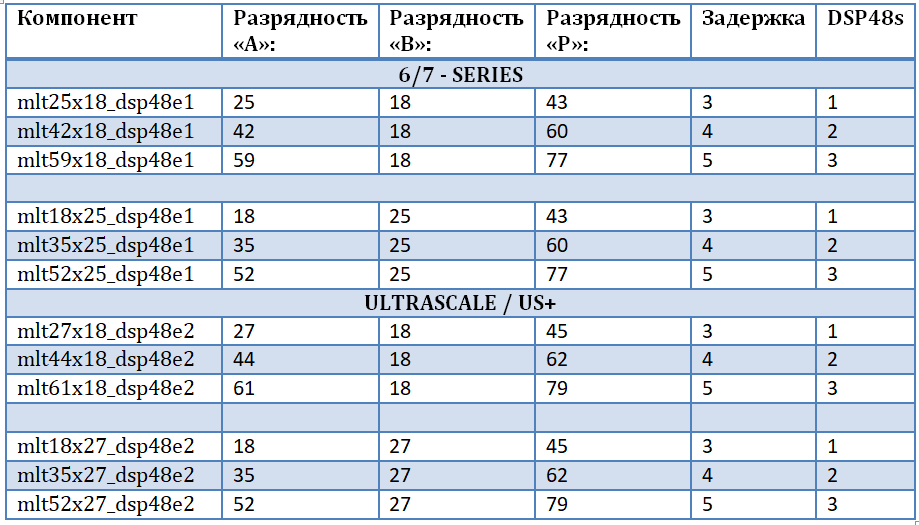
Peningkatan kedalaman bit lebih lanjut tidak menarik dalam kerangka tugas karena alasan yang dijelaskan di bawah ini:

Kedalaman faktor pembalikan

Diketahui bahwa semakin besar resolusi sinyal harmonik, semakin akurat jumlahnya muncul (semakin banyak tanda di bagian fraksional). Tetapi ukuran bit port adalah B <25 bit karena fakta bahwa untuk faktor-faktor rotasi dalam node FFT, kedalaman bit ini cukup untuk memastikan penggandaan kualitas tinggi dari input stream dengan elemen sinyal harmonik dalam "kupu-kupu" (untuk setiap panjang FFT yang dapat dicapai secara realistis pada FPGA modern). Nilai khas dari kedalaman bit dari koefisien balik dalam tugas yang saya laksanakan adalah 16 bit, 24 - lebih jarang, 32 - tidak pernah.

Kedalaman sampel input sedikit

Kapasitas node penerimaan dan perekaman (ADCs, DACs) ini tidak besar - dari 8 hingga 16 bit, dan jarang - 24 atau 32 bit. Selain itu, dalam kasus yang terakhir, akan lebih efisien untuk menggunakan format data floating point sesuai dengan standar IEEE-754. Di sisi lain, setiap tahap "kupu-kupu" di FFT menambahkan satu bit data ke sampel keluaran karena operasi matematika. Misalnya, untuk panjang NFFT = 1024, log2 (NFFT) = 10 kupu-kupu digunakan.

Oleh karena itu, kedalaman bit output akan sepuluh bit lebih besar dari input, WOUT = WIN + 10. Secara umum, rumusnya terlihat seperti ini:

WOUT = WIN + log2 (NFFT);

Contoh:

Kedalaman bit dari aliran input MENANG = 32 bit,
Kedalaman bit dari faktor belok TWD = 27,
Kapasitas port “A” dari daftar pengganda yang diimplementasikan dalam artikel ini tidak melebihi 52 bit. Ini berarti bahwa jumlah maksimum kupu-kupu adalah FFT = 52-32 = 20. Artinya, dimungkinkan untuk mewujudkan FFT dengan panjang hingga 2 ^ 20 = 1M sampel. (Namun, dalam praktiknya, ini tidak mungkin dengan cara langsung karena sumber daya yang terbatas bahkan untuk kristal FPGA yang paling kuat, tetapi ini berkaitan dengan topik lain dan tidak akan dipertimbangkan dalam artikel).

Seperti yang Anda lihat, ini adalah salah satu alasan utama mengapa saya tidak mengimplementasikan pengganda dengan kedalaman bit input port yang lebih tinggi. Pengganda yang digunakan mencakup berbagai ukuran bit input yang diperlukan dan faktor rotasi untuk tugas menghitung FFT integer. Dalam semua kasus lain, Anda dapat menggunakan perhitungan FFT dalam format floating point !

Implementasi pengganda "lebar"

Berdasarkan contoh sederhana mengalikan dua angka yang tidak sesuai dengan kedalaman bit dari simpul DSP48 standar, saya akan menunjukkan bagaimana Anda dapat mengimplementasikan pengganda data yang luas. Gambar berikut menunjukkan diagram bloknya. Pengganda mengimplementasikan perkalian dua angka yang ditandatangani dalam kode tambahan, lebar operan X pertama adalah 42 bit, Y kedua adalah 18 bit. Ini berisi dua node DSP48E2. Dua register digunakan untuk menyamakan penundaan di simpul atas. Ini dilakukan karena di adder atas Anda perlu menambahkan angka dengan benar dari simpul atas dan bawah DSP48. Pengiklan bawah sebenarnya tidak digunakan. Pada output dari simpul bawah ada penundaan tambahan produk untuk menyelaraskan nomor keluaran dengan waktu. Total keterlambatan adalah 4 siklus.



Pekerjaan terdiri dari dua komponen:

• Bagian termuda: P1 = '0' & X [16: 0] * Y [17: 0];
• Bagian yang lebih tua: P2 = X [42:17] * Y [17: 0] + (P1 >> 17);

Penghancur

Seperti pengganda, penambah dapat dibangun di atas sumber daya logis menggunakan rantai transfer, atau di blok DSP48. Untuk mencapai throughput maksimum, metode kedua lebih disukai. Satu DSP48 primitif memungkinkan implementasi operasi penambahan hingga 48 bit, dua node hingga 96 bit. Untuk tugas saat ini, kedalaman bit tersebut cukup. Selain itu, DSP48 primitif memiliki mode "SIMD MODE" khusus, yang memaralelkan ALU 48-bit bawaan ke dalam beberapa operasi dengan data yang berbeda dari kapasitas kecil. Yaitu, dalam mode “SATU” digunakan kisi bit penuh 48 bit dan dua operan, dan dalam mode “DUA” kisi bit dibagi menjadi beberapa aliran paralel masing-masing 24 bit (4 operan). Mode ini, dengan menggunakan hanya satu penambah, membantu mengurangi jumlah sumber daya chip FPGA yang diduduki pada kedalaman bit sampel sampel yang kecil (pada tahap pertama perhitungan).

Peningkatan kedalaman bit

Operasi mengalikan dua angka dengan bit N dan M dalam kode tambahan biner mengarah pada peningkatan kapasitas bit output ke P = N + M.

Contoh: untuk mengalikan angka tiga-bit N = M = 3, angka positif maksimum adalah +3 = (011) ₂ , dan angka negatif maksimum adalah 4 = (100) ₂ . Bit paling signifikan bertanggung jawab atas tanda nomor. Oleh karena itu, jumlah maksimum yang mungkin ketika mengalikan adalah +16 = (010000) ₂ , yang dibentuk sebagai hasil dari mengalikan dua angka negatif maksimum -4. Kedalaman bit dari output sama dengan jumlah bit input P = N + M = 6 bit.

Operasi menambahkan dua angka dengan bit N dan M dalam kode tambahan biner mengarah pada peningkatan bit output dengan satu bit.

Contoh: tambahkan dua angka positif, N = M = 3, angka positif maksimum adalah 3 = (011) ₂ , dan angka negatif maksimum adalah 4 = (100) ₂ .Bit paling signifikan bertanggung jawab atas tanda nomor. Oleh karena itu, angka positif maksimum adalah 6 = (0110) ₂ , dan angka negatif maksimum adalah -8 = (1000) ₂ . Resolusi output meningkat satu bit.

Pertimbangan fitur algoritma

Pemotongan kedalaman bit dari atas:
Untuk meminimalkan sumber daya FPGA dalam algoritma FFT, diputuskan bahwa ketika mengalikan data dalam kupu-kupu, jangan pernah menggunakan angka negatif maksimum yang mungkin untuk mengubah koefisien. Amandemen ini tidak mempengaruhi hasil. Misalnya, ketika menggunakan representasi 16-bit dari faktor rotasi, angka minimum adalah -32768 = 0x8000, dan yang berikutnya -32767 = 0x8001. Kesalahan saat mengganti angka negatif maksimum dengan nilai tetangga terdekat akan ~ 0,003% dan sepenuhnya dapat diterima untuk tugas tersebut.

Dengan menghapus angka minimum dalam produk dua angka, pada setiap iterasi Anda dapat mengurangi satu bit orde tinggi yang tidak terpakai. Contoh: data - 4 = (100) ₂ , koefisien +3 = (011) ₂. Hasil Multiplikasi = -12 = (110100) ₂ . Bit kelima bisa dibuang karena duplikat tetangga, yang keempat adalah sedikit tanda.

Pemotongan bit dari bawah:

Jelas, mengalikan sinyal input dalam "kupu-kupu" dengan efek harmonik, tidak perlu menarik kedalaman bit output ke kupu-kupu berikutnya, tetapi pembulatan atau pemotongan diperlukan. Rotating factor disajikan dalam format M-bit yang nyaman, tetapi pada kenyataannya itu adalah sinus normal dan cosinus dinormalisasi menjadi satu. Yaitu, angka 0x8000 = -1, dan angka 0x7FFF = +1. Oleh karena itu, hasil penggandaan harus dipotong ke kedalaman bit asli dari data (yaitu, bit M dari faktor-faktor yang berputar dipotong dari bawah). Dalam semua implementasi FFT yang kebetulan saya lihat, faktor balik dinormalisasi menjadi 1 dengan satu atau lain cara. Oleh karena itu, dari hasil perkalian perlu untuk mengambil bit dalam kisi berikut [N + M-1-1: M-1]. Bit yang paling signifikan tidak digunakan (kurangi 1 tambahan), bit paling tidak signifikan dipotong.

Penambahan / pengurangan data dalam operasi "kupu-kupu" tidak diminimalisasi dengan cara apa pun, dan hanya operasi ini yang berkontribusi terhadap peningkatan kedalaman bit dari data output dengan satu bit pada setiap tahap perhitungan .

Perhatikan bahwa pada tahap pertama dari algoritma DFT FFT atau pada tahap terakhir dari algoritma FFT DIF, data harus dikalikan dengan faktor balik dengan indeks nol W0 = {Re, Im} = {1, 0}. Karena fakta bahwa perkalian dengan persatuan dan nol adalah operasi primitif, mereka dapat dihilangkan. Dalam hal ini, operasi multiplikasi kompleks tidak diperlukan sama sekali: komponen nyata dan imajiner mengalami "belokan" tanpa perubahan. Pada tahap kedua, dua koefisien digunakan: W0 = {Re, Im} = {1, 0} dan W1 = {Re, Im} = {0, -1}. Demikian pula, operasi dapat direduksi menjadi transformasi elementer dan menggunakan multiplexer untuk memilih sampel keluaran. Ini memungkinkan Anda untuk secara signifikan menyimpan blok DSP48 pada dua kupu-kupu pertama.

Pengganda kompleks dibangun dengan cara yang sama - berdasarkan pengganda dan pengurang-penambah, untuk beberapa opsi untuk kedalaman bit data input, sumber daya tambahan tidak diperlukan, yang akan dijelaskan di bawah ini.

Garis input buffer dan delay dan cross-switch mirip dengan yang dijelaskan dalam artikel sebelumnya. Rotating factor menjadi bilangan bulat dengan kedalaman bit yang dapat dikonfigurasi. Kalau tidak, tidak ada perubahan global dalam desain inti FFT.

Fitur inti FFT INT_FFTK

• Skema pemrosesan data sepenuhnya pipelined.
• Panjang konversi NFFT = 8-512K poin.
• Penyesuaian panjang konversi NFFT yang fleksibel.
• Format input integer, lebar bit dapat dikonfigurasi.
• Format bilangan bulat dari faktor rotari, lebar bit dapat dikonfigurasi.
• .
• !
• .
• : – , -.
• : - , – .
• . Radix-2.
• NFFT *.
• .
• (Virtex-6, 7-Series, Ultrascale).
• ~375MHz Kintex-7
• – VHDL.
• bitreverse +.
• Proyek open source tanpa menyertakan IP-core pihak ketiga.

Kode sumber

Kode sumber untuk kernel FFT INTFFTK pada VHDL (termasuk operasi dasar dan satu set pengganda) dan skrip m untuk Matlab / Octave tersedia di profil saya di github .

Kesimpulan

Selama pengembangan, inti FFT baru dirancang, yang memberikan kinerja lebih besar dibandingkan dengan rekan-rekan. Kombinasi core FFT dan OBPF tidak memerlukan terjemahan ke dalam urutan alami, dan panjang konversi maksimum hanya dibatasi oleh sumber daya FPGA. Konkurensi ganda memungkinkan Anda memproses aliran input frekuensi ganda, yang tidak dapat dilakukan IP-CORE Xilinx. Kedalaman bit pada output integer FFT meningkat secara linear tergantung pada jumlah tahap konversi.

Dalam artikel sebelumnya, saya menulis tentang rencana masa depan: inti FFT Radix-4, Radix-8, Ultra-Long FFT untuk jutaan poin, FFT-FP32 (dalam format IEEE-754). Singkatnya, hampir semuanya diizinkan, tetapi karena satu dan lain alasan, saat ini mereka tidak dapat dipublikasikan. Pengecualiannya adalah algoritma FFT Radix-8, yang bahkan tidak saya pedulikan (sulit dan malas).

Sekali lagi, saya mengucapkan terima kasih kepada dsmv2014 , yang selalu menyambut ide-ide petualangan saya. Terima kasih atas perhatian anda!

PEMBARUAN 2018/08/22

Menambahkan opsi SCALED FFT / IFFT ke kode sumber . Pada setiap kupu-kupu, kedalaman bit dipotong oleh 1 bit (truncate LSB). Output bit depth = kedalaman bit input.

Selain itu, saya akan memberikan dua grafik lintasan sinyal nyata melalui FPGA untuk menunjukkan properti integral dari transformasi, yaitu: bagaimana pemotongan mempengaruhi hasil akumulasi kesalahan pada output FFT. Dari teori diketahui bahwa sebagai hasil dari transformasi Fourier, sinyal-to-noise ratio memburuk ketika sinyal input terpotong relatif terhadap versi non-terpotong.

Contoh: Amplitudo dari amplitudo input adalah 6 bit. Sinyal adalah gelombang sinus pada 128 sampel PF. NFFT = 1024 sampel, DATA_WIDTH = 16, TWDL_WIDTH = 16.

Seperti yang Anda lihat, opsi SCALED tidak "menarik" gelombang sinus keluar dari kebisingan, sementara opsi UNSCALED menunjukkan hasil yang baik.