Ikhtisar Algoritma Wawancara Kerja - Mengatur Generasi

Halo, Habr!

Posting ini memulai analisis tugas sesuai dengan algoritma yang perusahaan IT besar (Mail.Ru Group, Google, dll) suka memberikan kandidat untuk wawancara (jika wawancara dengan algoritma tidak baik, maka peluang mendapatkan pekerjaan di perusahaan impian, sayangnya cenderung nol). Pertama-tama, posting ini berguna bagi mereka yang tidak memiliki pengalaman pemrograman olimpiade atau kursus berat seperti ShAD atau LKS, di mana topik algoritma dianggap cukup serius, atau bagi mereka yang ingin menyegarkan pengetahuan mereka di bidang tertentu.

Pada saat yang sama, tidak dapat diperdebatkan bahwa semua tugas yang akan ditangani di sini tentu akan dipenuhi pada saat wawancara, namun, pendekatan di mana tugas-tugas tersebut diselesaikan serupa dalam kebanyakan kasus.

Narasi akan dibagi menjadi beberapa topik yang berbeda, dan kita akan mulai dengan menghasilkan set dengan struktur tertentu.

1. Mari kita mulai dengan tombol akordeon: Anda perlu membuat semua urutan braket yang benar dengan tanda kurung dari tipe yang sama ( apa urutan braket yang benar ), di mana jumlah tanda kurung adalah k.

Masalah ini dapat diselesaikan dengan beberapa cara. Mari kita mulai dengan rekursif .

Metode ini mengasumsikan bahwa kita mulai mengulangi urutan dari daftar kosong. Setelah braket (membuka atau menutup) ditambahkan ke daftar, panggilan rekursi dilakukan lagi dan kondisinya diperiksa. Apa saja kondisinya? Penting untuk memantau perbedaan antara tanda kurung buka dan tutup (variabel cnt ) - Anda tidak dapat menambahkan braket penutup ke daftar jika perbedaan ini tidak positif, jika tidak, urutan braket tidak akan lagi benar. Tetap menerapkannya dalam kode dengan hati-hati.

 k = 6 #   init = list(np.zeros(k)) #  ,    cnt = 0 #    ind = 0 # ,       def f(cnt, ind, k, init): #  . ,     if (cnt <= k-ind-2): init[ind] = '(' f(cnt+1, ind+1, k, init) # .    ,  cnt > 0 if cnt > 0: init[ind] = ')' f(cnt-1, ind+1, k, init) #      if ind == k: if cnt == 0: print (init) 

Kompleksitas dari algoritma ini adalah $$$O ((C_k ^ {k / 2} - C_k ^ {k / 2 -1}) * k)$ diperlukan memori tambahan $$$O (k)$ .

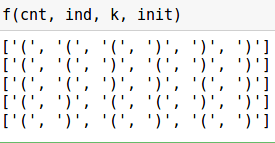
Dengan parameter yang diberikan, pemanggilan fungsi $$$f (cnt, ind, k, init)$ akan menampilkan yang berikut:

Cara berulang untuk menyelesaikan masalah ini: dalam kasus ini, idenya akan berbeda secara mendasar - Anda perlu memperkenalkan konsep urutan leksikografis untuk urutan braket.

Semua urutan kurung yang benar untuk satu jenis kurung dapat dipesan dengan mempertimbangkan fakta itu $$$'(' <')'$ . Misalnya, untuk n = 6, urutan yang paling rendah secara leksikografis adalah $$$((()))$ dan yang tertua - $$$() () ()$ .

Untuk mendapatkan urutan leksikografis berikutnya, Anda perlu menemukan braket pembuka paling kanan, sebelum ada braket penutup, sehingga ketika mereka dipertukarkan, urutan braket tetap benar. Kami menukar mereka dan menjadikan suffix minor yang paling leksikografis - untuk ini Anda perlu menghitung pada setiap langkah perbedaan antara jumlah tanda kurung.

Menurut pendapat saya, pendekatan ini sedikit suram daripada rekursif, tetapi dapat digunakan untuk memecahkan masalah lain dalam menghasilkan set. Kami menerapkan ini dalam kode.

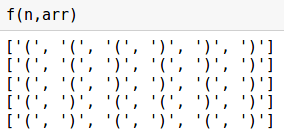
 #  ,    n = 6 arr = ['(' for _ in range(n//2)] + [')' for _ in range(n//2)] def f(n, arr): #    print (arr) while True: ind = n-1 cnt = 0 #  . ,    while ind>=0: if arr[ind] == ')': cnt -= 1 if arr[ind] == '(': cnt += 1 if cnt < 0 and arr[ind] =='(': break ind -= 1 #   ,     if ind < 0: break #   .  arr[ind] = ')' #      for i in range(ind+1,n): if i <= (n-ind+cnt)/2 +ind: arr[i] = '(' else: arr[i] = ')' print (arr) 

Kompleksitas algoritma ini sama dengan contoh sebelumnya.

Ngomong-ngomong, ada metode sederhana yang menunjukkan bahwa jumlah urutan braket yang dihasilkan untuk n / 2 yang diberikan harus cocok dengan angka Catalan .

Itu berhasil!

Luar biasa, dengan tanda kurung untuk saat ini, mari beralih ke menghasilkan subset. Mari kita mulai dengan teka-teki sederhana.

2. Diberikan array urutan naik dengan nomor dari $$$0$ sebelumnya $$$n-1$ , diperlukan untuk menghasilkan semua himpunan bagiannya.

Perhatikan bahwa jumlah himpunan bagian dari himpunan tersebut tepat $$$2 ^ n$ . Jika setiap subset direpresentasikan sebagai array indeks, di mana $$$0$ berarti bahwa elemen tersebut tidak termasuk dalam set, tetapi $$$1$ - apa yang disertakan, maka generasi semua array tersebut akan menjadi generasi semua subset.

Jika kita mempertimbangkan representasi angka bitwise dari 0 hingga $$$2 ^ n - 1$ , maka mereka akan menentukan himpunan bagian yang diinginkan. Artinya, untuk memecahkan masalah, perlu untuk menerapkan penambahan kesatuan ke nomor biner. Kita mulai dengan semua nol dan diakhiri dengan array di mana ada satu unit.

 n = 3 B = np.zeros(n+1) #  B   1  (    ) a = np.array(list(range(n))) #   def f(B, n, a): #   while B[0] == 0: ind = n #     while B[ind] == 1: ind -= 1 #   1 B[ind] = 1 #      B[(ind+1):] = 0 print (a[B[1:].astype('bool')]) 

Kompleksitas dari algoritma ini adalah $$$O (n * 2 ^ n)$ , dari memori - $$$O (n)$ .

Sekarang mari kita sedikit mempersulit tugas sebelumnya.

3. Diberikan array yang dipesan dalam urutan menaik dengan angka dari $$$0$ sebelumnya $$$n-1$ , Anda harus menghasilkan semuanya $$$k$ himpunan bagian elemen (dipecahkan secara iteratif).

Saya perhatikan bahwa rumusan masalah ini mirip dengan yang sebelumnya dan dapat diselesaikan dengan menggunakan metodologi yang kira-kira sama: ambil larik awal dengan $$$k$ unit dan $$$n-k$ nol dan secara berurutan memilah-milah semua varian sekuens panjang tersebut $$$n.$

Namun, perubahan kecil diperlukan. Kita perlu memilah-milah segalanya $$$k$ -nilai set angka dari $$$0$ sebelumnya $$$n-1$ . Anda perlu memahami dengan tepat bagaimana Anda perlu menyortir subset. Dalam hal ini, kami dapat memperkenalkan konsep urutan leksikografis untuk perangkat tersebut.

Kami juga mengatur urutan dengan kode karakter: $$$1 <0$ (Ini, tentu saja, aneh, tetapi itu perlu, dan sekarang kita akan mengerti mengapa). Misalnya, untuk $$$n = 4, k = 2$ yang termuda dan tertua adalah urutannya $$$[1,1,0,0]$ dan $$$[0,0,1,1]$ .

Masih memahami bagaimana menggambarkan transisi dari satu urutan ke urutan lainnya. Semuanya sederhana di sini: jika kita berubah $$$1$ pada $$$0$ , lalu di sebelah kiri kita tulis leksikografis minimal dengan mempertimbangkan kelestarian kondisi pada $$$k$ . Kode:

 n = 5 k = 3 a = np.array(list(range(n))) #    k -   init = [1 for _ in range(k)] + [0 for _ in range(nk)] def f(a, n, k, init): #   k-  print (a[a[init].astype('bool')]) while True: unit_cnt = 0 cur_ind = 0 #   ,     1 while (cur_ind < n) and (init[cur_ind]==1 or unit_cnt==0): if init[cur_ind] == 1: unit_cnt += 1 cur_ind += 1 #        -    if cur_ind == n: break #  init[cur_ind] = 1 #   . .  for i in range(cur_ind): if i < unit_cnt-1: init[i] = 1 else: init[i] = 0 print (a[a[init].astype('bool')]) 

Contoh kerja:

Kompleksitas dari algoritma ini adalah $$$O (C_n ^ k * n)$ , dari memori - $$$O (n)$ .

4. Diberikan array urutan naik dengan nomor dari $$$0$ sebelumnya $$$n-1$ , Anda harus menghasilkan semuanya $$$k$ himpunan bagian elemen (selesaikan secara rekursif).

Sekarang mari kita coba rekursi. Idenya sederhana: kali ini tanpa deskripsi, lihat kodenya.

 n = 5 a = np.array(list(range(n))) ind = 0 # ,       num = 0 # ,       k = 3 sub = list(-np.ones(k)) #  def f(n, a, num, ind, k, sub): #   k  ,     if ind == k: print (sub) else: for i in range(n - num): #  ,      k  if (n - num - i >= k - ind): #      sub[ind] = a[num + i] #     f(n, a, num+1+i, ind+1, k, sub) 

Contoh kerja:

Kompleksitasnya sama seperti pada metode sebelumnya.

5. Diberikan array urutan naik dengan nomor dari $$$0$ sebelumnya $$$n-1$ , diperlukan untuk menghasilkan semua permutasi.

Kami akan memecahkan menggunakan rekursi. Solusinya mirip dengan yang sebelumnya, di mana kami memiliki daftar tambahan. Awalnya nol jika menyala $$$i$ -Tempat elemen adalah unit, lalu elemen $$$i$ sudah dalam permutasi. Tidak lebih cepat dikatakan daripada dilakukan:

 a = np.array(range(3)) n = a.shape[0] ind_mark = np.zeros(n) #   perm = -np.ones(n) #     def f(ind_mark, perm, ind, n): if ind == n: print (perm) else: for i in range(n): if not ind_mark[i]: #     ind_mark[i] = 1 #   perm[ind] = i f(ind_mark, perm, ind+1, n) #   -    ind_mark[i] = 0 

Contoh kerja:

Kompleksitas dari algoritma ini adalah $$$O (n ^ 2 * n!)$ , dari memori - $$$O (n).$

Sekarang pertimbangkan dua teka-teki yang sangat menarik untuk kode Gray . Singkatnya, ini adalah serangkaian urutan dengan panjang yang sama, di mana setiap urutan berbeda dari tetangganya dalam satu kategori.

6. Hasilkan semua kode abu-abu dua dimensi dengan panjang n.

Gagasan untuk memecahkan masalah ini keren, tetapi jika Anda tidak tahu solusinya, maka itu bisa sangat sulit untuk dipikirkan. Saya perhatikan bahwa jumlah urutan tersebut adalah $$$2 ^ n$ .

Kami akan menyelesaikannya secara berulang. Misalkan kita membuat beberapa bagian dari sekuens semacam itu dan mereka berada dalam beberapa daftar. Jika kita menduplikasi daftar tersebut dan menulisnya dalam urutan terbalik, maka urutan terakhir dalam daftar pertama bertepatan dengan urutan pertama dalam daftar kedua, yang kedua dari belakang bertepatan dengan yang kedua, dll. Gabungkan daftar ini menjadi satu.

Apa yang perlu dilakukan agar semua urutan dalam daftar berbeda satu sama lain dalam kategori yang sama? Letakkan satu unit di tempat yang sesuai di elemen daftar kedua untuk mendapatkan kode Gray.

Sulit untuk mempersepsikan "oleh telinga", kami akan menggambarkan iterasi dari algoritma ini.

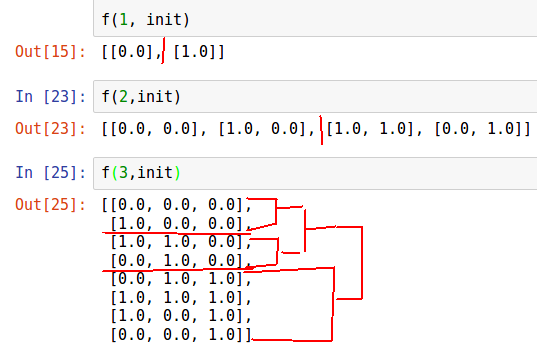
 n = 3 init = [list(np.zeros(n))] def f(n, init): for i in range(n): for j in range(2**i): init.append(list(init[2**i - j - 1])) init[-1][i] = 1.0 return init 

Kompleksitas dari tugas ini adalah $$$O (n * 2 ^ n)$ , dari memori sama.

Sekarang mari kita rumit tugasnya.

7. Hasilkan semua kode abu-abu k-dimensional panjang n.

Jelas bahwa tugas yang lalu hanya merupakan kasus khusus dari tugas ini. Namun, dengan cara yang indah bahwa tugas masa lalu diselesaikan, ini tidak dapat diselesaikan, di sini perlu untuk memilah urutan dalam urutan yang benar. Mari kita dapatkan array dua dimensi $$$k * n$ . Awalnya, baris terakhir memiliki unit, dan sisanya memiliki nol. Selain itu, dalam matriks, $$$-1$ . Di sini $$$1$ dan $$$-1$ berbeda satu sama lain dalam arah: $$$1$ menunjuk ke atas $$$-1$ menunjuk ke bawah. Penting: di setiap kolom setiap saat hanya ada satu $$$1$ atau $$$-1$ , dan angka yang tersisa akan menjadi nol.

Sekarang kita akan mengerti bagaimana mungkin untuk memilah urutan ini untuk mendapatkan kode Gray. Mulai dari akhir untuk memindahkan elemen ke atas.

Pada langkah berikutnya, kami mencapai langit-langit. Kami menulis urutan yang dihasilkan. Setelah mencapai batas, Anda harus mulai bekerja dengan kolom berikutnya. Anda perlu mencarinya dari kanan ke kiri, dan jika kami menemukan kolom yang dapat dipindahkan, maka untuk semua kolom yang tidak dapat kami kerjakan, panah akan berubah ke arah yang berlawanan sehingga mereka dapat dipindahkan lagi.

Sekarang Anda dapat memindahkan kolom pertama ke bawah. Kami memindahkannya sampai menyentuh lantai. Begitu seterusnya, sampai semua panah menghantam lantai atau langit-langit dan tidak ada kolom yang tersisa yang bisa dipindahkan.

Namun, dalam rangka penghematan memori, kami akan menyelesaikan masalah ini menggunakan dua array satu dimensi panjang $$$n$ : dalam satu array elemen dari urutan itu sendiri akan terletak, dan yang lain dari arah mereka (panah).

 n,k = 3,3 arr = np.zeros(n) direction = np.ones(n) #   ,    def k_dim_gray(n,k): #    print (arr) while True: ind = n-1 while ind >= 0: #    ,    if (arr[ind] == 0 and direction[ind] == 0) or (arr[ind] == k-1 and direction[ind] == 1): direction[ind] = (direction[ind]+1)%2 else: break ind -= 1 #     ,     if ind < 0: break #    1 ,   1  arr[ind] += direction[ind]*2 - 1 print (arr) 

Contoh kerja:

Kompleksitas dari algoritma ini adalah $$$O (n * k ^ n)$ , dari memori - $$$O (n)$ .

Ketepatan algoritma ini dibuktikan dengan induksi aktif $$$n$ , di sini saya tidak akan menjelaskan buktinya.

Pada posting selanjutnya kita akan menganalisis tugas untuk dinamika.