Prinsip tindakan paling tidak. Bagian 1

Ketika saya pertama kali mempelajari tentang prinsip ini, saya merasakan semacam mistisisme. Tampaknya alam secara misterius melewati semua jalur yang mungkin dari sistem dan memilih yang terbaik dari mereka.

Hari ini saya ingin berbicara sedikit tentang salah satu prinsip fisik yang paling luar biasa - prinsip tindakan paling tidak.

Latar belakang

Sejak zaman Galileo, diketahui bahwa tubuh yang tidak terpengaruh oleh kekuatan bergerak dalam garis lurus, yaitu sepanjang jalur terpendek. Sinar cahaya merambat dalam garis lurus.

Saat dipantulkan, cahaya juga bergerak sedemikian rupa untuk berpindah dari satu titik ke titik lainnya dengan cara terpendek. Dalam gambar, jalur terpendek akan menjadi jalur hijau di mana sudut datang sama dengan sudut pantulan. Jalur lain apa pun, seperti merah, akan lebih panjang.


Ini mudah dibuktikan dengan hanya memantulkan jalur sinar ke sisi berlawanan dari cermin. Dalam gambar mereka ditampilkan dengan garis putus-putus.


Dapat dilihat bahwa jalur hijau ACB berubah menjadi ACB langsung. Dan jalur merah berubah menjadi garis putus-putus ADB, yang tentu saja lebih panjang dari hijau.

Pada tahun 1662, Pierre Fermat menyarankan bahwa kecepatan cahaya dalam zat padat, misalnya, dalam gelas, kurang dari di udara. Sebelum ini, ada versi Descartes yang diterima secara umum, yang menurutnya kecepatan cahaya dalam materi harus lebih besar daripada di udara untuk mendapatkan hukum refraksi yang benar. Bagi Fermat, anggapan bahwa cahaya dapat bergerak dalam media yang lebih padat lebih cepat daripada yang langka tampaknya tidak wajar. Oleh karena itu, ia menyarankan bahwa segala sesuatu adalah kebalikannya dan terbukti merupakan hal yang luar biasa - berdasarkan asumsi ini, cahaya dibiaskan untuk mencapai tujuannya dalam waktu sesingkat mungkin.


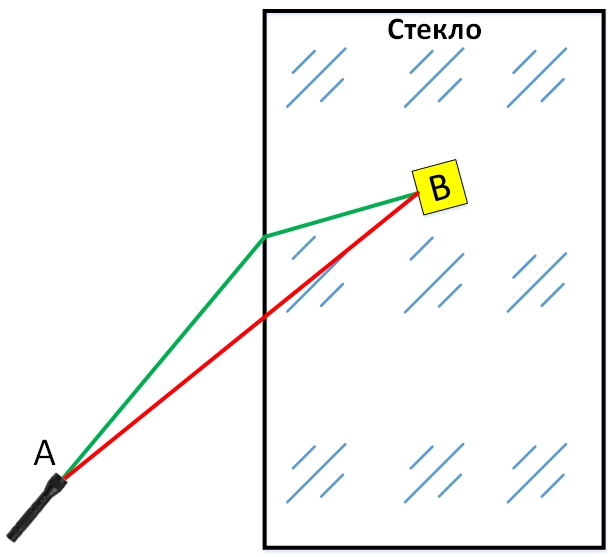
Dalam gambar itu lagi, warna hijau menunjukkan jalur di mana berkas cahaya benar-benar bergerak. Jalur yang ditandai dengan warna merah adalah yang terpendek, tetapi bukan yang tercepat, karena cahaya memiliki jalur yang lebih besar untuk melewati kaca, dan kecepatannya lebih lambat di dalamnya. Yang tercepat adalah jalur nyata dari berkas cahaya.

Semua fakta ini menunjukkan bahwa alam bertindak secara rasional, bahwa cahaya dan tubuh bergerak paling optimal, menghabiskan usaha sesedikit mungkin. Namun upaya macam apa itu, dan bagaimana cara menghitungnya, tetap menjadi misteri.

Pada 1744, Maupertuis memperkenalkan konsep "aksi" dan merumuskan prinsip yang menurutnya lintasan sebenarnya dari suatu partikel berbeda dari yang lain sehingga tindakannya minimal. Namun, Maupertuis sendiri tidak bisa memberikan definisi yang jelas tentang apa tindakan ini sama dengan. Formulasi matematis yang ketat dari prinsip tindakan paling tidak sudah dikembangkan oleh matematikawan lain - Euler, Lagrange, dan akhirnya diberikan oleh William Hamilton:


Dalam bahasa matematika, prinsip tindakan paling tidak dirumuskan secara singkat, tetapi tidak semua pembaca dapat memahami arti dari notasi yang digunakan. Saya ingin mencoba menjelaskan prinsip ini dengan lebih jelas dan dengan kata-kata sederhana.

Tubuh bebas

Jadi bayangkan Anda duduk di mobil pada suatu titik $$ dan tepat waktu $$ Anda telah diberi tugas sederhana: pada saat itu $$ Anda perlu sampai ke titik dengan mobil $$ .


Bahan bakar untuk mobil itu mahal dan, tentu saja, Anda ingin membelanjakannya sesedikit mungkin. Mobil Anda dibuat menggunakan teknologi super terbaru dan dapat mempercepat atau mengerem secepat yang Anda suka. Namun, ia dirancang agar semakin cepat, semakin banyak bahan bakar yang dikonsumsi. Selain itu, konsumsi bahan bakar sebanding dengan kuadrat kecepatan. Jika Anda mengemudi dua kali lebih cepat, maka untuk periode waktu yang sama Anda mengonsumsi bahan bakar 4 kali lebih banyak. Selain kecepatan, massa mobil juga memengaruhi konsumsi bahan bakar. Semakin berat mobil kami, semakin banyak bahan bakar yang dikonsumsi. Konsumsi bahan bakar mobil kami pada waktu tertentu adalah $$ , yaitu persis energi kinetik mobil.

Jadi, bagaimana Anda harus pergi ke titik $$ ke waktu yang ditentukan tepat dan menggunakan bahan bakar sesedikit mungkin? Jelas bahwa Anda harus pergi dalam garis lurus. Dengan peningkatan jarak mengemudi, bahan bakar akan dikonsumsi persis tidak kurang. Dan kemudian Anda dapat memilih taktik yang berbeda. Misalnya, Anda dapat dengan cepat sampai pada intinya $$ di muka dan hanya duduk, tunggu, ketika saatnya tiba $$ . Kecepatan mengemudi, dan karenanya konsumsi bahan bakar pada waktu tertentu, akan berubah menjadi besar, tetapi waktu mengemudi juga akan berkurang. Mungkin total konsumsi bahan bakar dalam kasus ini tidak akan terlalu besar. Atau Anda bisa naik secara merata, pada kecepatan yang sama, sehingga, tanpa terburu-buru, tiba pada suatu waktu $$ . Atau bagian dari cara mengemudi cepat, dan sebagian lebih lambat. Apa cara yang lebih baik untuk pergi?

Ternyata cara paling optimal, paling ekonomis untuk mengemudi adalah mengemudi dengan kecepatan konstan, seperti berada di suatu titik $$ pada waktu yang ditentukan tepat $$ . Dengan opsi lain, bahan bakar akan lebih banyak dikonsumsi. Anda dapat memeriksanya sendiri dengan beberapa contoh. Alasannya adalah bahwa konsumsi bahan bakar meningkat sebanding dengan kuadrat kecepatan. Oleh karena itu, ketika kecepatan meningkat, konsumsi bahan bakar meningkat lebih cepat daripada waktu mengemudi berkurang, dan konsumsi bahan bakar secara keseluruhan juga meningkat.

Jadi, kami menemukan bahwa jika sebuah mobil pada suatu waktu mengkonsumsi bahan bakar sebanding dengan energi kinetiknya, maka cara paling ekonomis untuk mendapatkannya dari suatu titik $$ to the point $$ untuk waktu yang ditentukan secara tepat adalah untuk naik secara seragam dan lurus, seperti halnya tubuh bergerak tanpa adanya gaya yang bekerja padanya. Cara mengemudi lainnya akan menghasilkan konsumsi bahan bakar keseluruhan yang lebih besar.

Dalam gravitasi

Sekarang mari kita tingkatkan mobil kita. Mari kita pasang mesin jet sehingga dapat terbang bebas ke segala arah. Secara umum, desainnya tetap sama, sehingga konsumsi bahan bakarnya tetap proporsional dengan energi kinetik mobil. Jika sekarang tugas diberikan untuk terbang keluar dari intinya $$ pada waktu $$ dan terbang ke titik $$ oleh waktu $$ , maka cara yang paling ekonomis, seperti sebelumnya, tentu saja, akan terbang secara seragam dan lurus, sampai pada suatu titik $$ pada waktu yang ditentukan tepat $$ . Ini lagi sesuai dengan gerakan bebas tubuh dalam ruang tiga dimensi.


Namun, perangkat yang tidak biasa dipasang pada model mobil terbaru. Unit ini dapat menghasilkan bahan bakar secara harfiah dari ketiadaan. Namun desainnya sedemikian rupa sehingga semakin tinggi mobil, semakin banyak bahan bakar yang dihasilkan perangkat pada setiap saat. Produksi bahan bakar berbanding lurus dengan tinggi $$ di mana mobil saat ini berada. Juga, semakin berat mobil, semakin kuat perangkat dipasang di atasnya dan semakin banyak bahan bakar yang dihasilkan, dan output berbanding lurus dengan massa mobil. $$ . Perangkat itu ternyata produksi bahan bakarnya sama persis $$ (dimana $$ - percepatan gravitasi), mis. energi potensial mobil.

Konsumsi bahan bakar pada setiap saat waktu sama dengan energi kinetik dikurangi energi potensial mobil (minus energi potensial, karena perangkat yang dipasang menghasilkan bahan bakar, dan tidak menghabiskan). Sekarang tugas kami adalah pergerakan mobil paling ekonomis di antara titik-titik $$ dan $$ semakin sulit. Gerakan seragam bujursangkar dalam hal ini bukan yang paling efektif. Ternyata lebih optimal untuk mendapatkan ketinggian sedikit, berlama-lama di sana, setelah mengembangkan lebih banyak bahan bakar, dan kemudian turun ke titik $$ . Dengan jalur penerbangan yang benar, total produksi bahan bakar akibat pendakian akan memblokir konsumsi bahan bakar tambahan dengan meningkatkan panjang jalur dan meningkatkan kecepatan. Jika Anda menghitung dengan cermat, maka dengan cara yang paling ekonomis untuk mobil, ia akan terbang di sepanjang parabola, persis di sepanjang lintasan seperti itu dan pada kecepatan yang sama persis seperti batu yang akan terbang di medan gravitasi bumi.


Penjelasan layak dilakukan di sini. Tentu saja Anda bisa dari titik itu $$ melempar batu dengan berbagai cara sehingga menyentuh satu titik $$ . Tetapi Anda harus membuangnya sehingga terbang keluar dari titik $$ pada waktu $$ tepat sasaran $$ tepat pada waktunya $$ . Gerakan ini akan menjadi yang paling ekonomis untuk mobil kami.

Fungsi Lagrange dan prinsip aksi paling tidak

Sekarang kita dapat mentransfer analogi ini ke tubuh fisik nyata. Sebuah analog dari intensitas konsumsi bahan bakar untuk bodi disebut fungsi Lagrange atau Lagrangian (untuk menghormati Lagrange) dan dilambangkan dengan huruf $$ . Lagrangian menunjukkan berapa banyak "bahan bakar" yang dikonsumsi tubuh pada saat tertentu. Untuk benda yang bergerak di bidang potensial, Lagrangian sama dengan energi kinetiknya, dikurangi energi potensial.

Sebuah analog dari jumlah total bahan bakar yang dikonsumsi untuk seluruh waktu pergerakan, yaitu nilai Lagrangian yang terakumulasi sepanjang waktu pergerakan disebut "aksi".

Prinsip tindakan paling tidak adalah bahwa tubuh bergerak sedemikian rupa sehingga tindakan (yang tergantung pada lintasan gerakan) minimal. Pada saat yang sama, seseorang tidak boleh lupa bahwa kondisi awal dan akhir ditentukan, mis. di mana tubuh berada pada suatu titik waktu $$ dan tepat waktu $$ .

Selain itu, bodi tidak harus bergerak dalam medan gravitasi yang seragam, yang kami pertimbangkan untuk mobil kami. Anda dapat mempertimbangkan situasi yang sama sekali berbeda. Tubuh dapat berosilasi pada pita elastis, mengayun pada pendulum atau terbang mengelilingi Matahari, dalam semua kasus ini bergerak sedemikian rupa untuk meminimalkan "total konsumsi bahan bakar" yaitu tindakan.

Jika sistem terdiri dari beberapa benda, maka bahasa Lagrangian dari sistem tersebut akan sama dengan total energi kinetik semua benda dikurangi total energi potensial seluruh tubuh. Dan lagi, semua badan akan bergerak secara terkoordinasi sehingga tindakan seluruh sistem dengan gerakan tersebut minimal.

Tidak sesederhana itu

Bahkan, saya sedikit curang dengan mengatakan bahwa tubuh selalu bergerak sedemikian rupa untuk meminimalkan tindakan. Meskipun dalam banyak kasus ini benar, Anda dapat menemukan situasi di mana tindakannya jelas tidak minimal.

Misalnya, ambil bola dan letakkan di ruang kosong. Tidak jauh dari situ, kami memasang dinding elastis. Misalkan kita ingin bola berada di tempat yang sama setelah beberapa waktu. Dalam kondisi seperti itu, bola bisa bergerak dengan dua cara berbeda. Pertama, itu bisa tetap di tempatnya. Kedua, bisa didorong ke arah dinding. Bola akan terbang ke dinding, memantul darinya dan kembali. Jelas bahwa Anda dapat mendorongnya begitu cepat sehingga ia kembali pada waktu yang tepat.


Kedua varian gerakan bola dimungkinkan, tetapi aksi dalam kasus kedua akan berubah lebih banyak, karena selama ini bola akan bergerak dengan energi kinetik yang tidak nol.

Bagaimana cara menyelamatkan prinsip tindakan paling tidak agar adil dalam situasi seperti itu? Kami akan membicarakan ini lain kali .