Perhitungan integral pasti: algoritma dasar

Publikasi ini menjelaskan metode paling sederhana untuk menghitung integral fungsi dari satu variabel pada suatu segmen, juga disebut rumus quadrature. Biasanya, metode ini diimplementasikan dalam perpustakaan matematika standar seperti Perpustakaan Ilmiah GNU untuk C, SciPy untuk Python, dan lainnya. Publikasi ini bertujuan untuk menunjukkan bagaimana metode ini bekerja "di bawah tenda", dan untuk menarik perhatian pada beberapa masalah akurasi dan kinerja algoritma. Saya juga ingin mencatat hubungan rumus quadrature dan metode integrasi numerik persamaan diferensial biasa, yang ingin saya tulis publikasi lain.

Definisi integral

Integral (menurut Riemann) dari suatu fungsi $$$f (x)$ di segmen tersebut $$$[a; b]$ Batas berikut disebut:

dimana $$$\ Delta x = \ max \ lbrace x_ {i + 1} - x_i \ rbrace$ - kehalusan partisi, $$$x_0 = a$ , $$$x_n = b$ , $$$\ xi_i$ - nomor sewenang-wenang di segmen tersebut $$$[x_i; x_ {i + 1}]$ .

Jika integral dari fungsi ada, maka nilai batasnya sama terlepas dari partisi, jika saja itu akan cukup kecil.

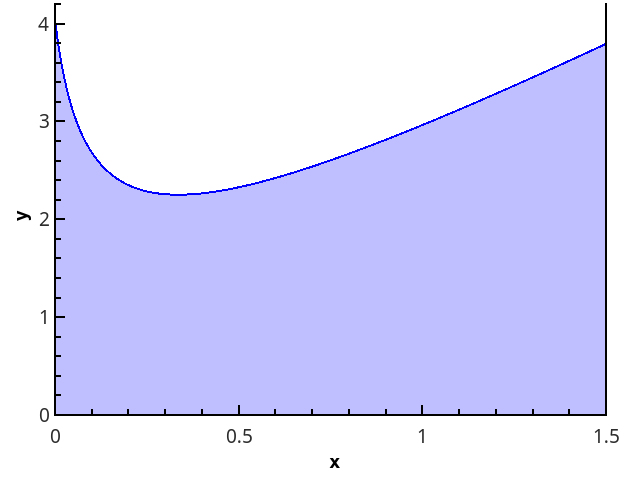
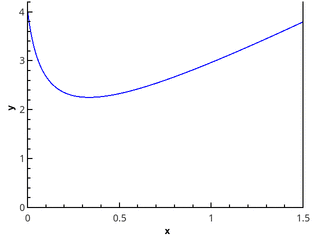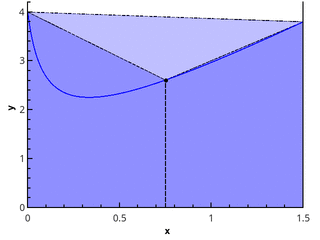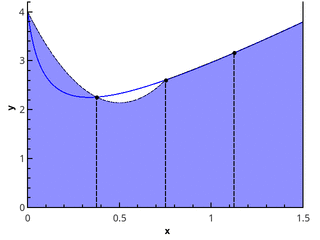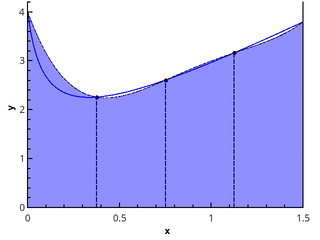
Definisi geometris lebih jelas - integralnya sama dengan luas trapesium melengkung yang dibatasi oleh sumbu 0 x , grafik fungsi, dan garis lurus x = a dan x = b (wilayah yang diisi pada gambar).

Rumus quadrature

Definisi integral (1) dapat ditulis ulang dalam bentuk

dimana $$$w_i$ - koefisien pembobotan, jumlah yang harus sama dengan 1, dan koefisien itu sendiri - cenderung nol dengan meningkatnya jumlah $$$n$ titik di mana fungsi dihitung.

Ekspresi (2) adalah dasar dari semua rumus quadrature (mis., Rumus untuk perkiraan perkiraan integral). Tantangannya adalah memilih titik $$$\ lbrace \ xi_i \ rbrace$ dan berat $$$w_i$ sehingga jumlah di sisi kanan mendekati integral yang diperlukan seakurat mungkin.

Tugas komputasi

Fungsi diatur $$$f (x)$ di mana ada algoritma untuk menghitung nilai di titik mana pun dalam interval $$$[a; b]$ (Maksud saya poin diwakili oleh angka floating-point - tidak ada fungsi Dirichlet di sana!).

Diperlukan untuk menemukan nilai perkiraan integral $$$\ int_a ^ bf (x) dx$ .
Solusi akan diimplementasikan dalam Python 3.6.

Untuk memeriksa metode, gunakan integral $$$\ int_0 ^ {3/2} \ kiri [2x + \ frac {1} {\ sqrt {x + 1/16}} \ kanan] dx = 17/4$ .

Perkiraan konstan konstan

Formula quadrature idealnya sederhana muncul dari penerapan ungkapan (1) "di dahi":

Karena dari metode membagi segmen dengan poin $$$\ lbrace x_i \ rbrace$ dan pilih titik $$$\ lbrace \ xi_i \ rbrace$ nilai batas tidak tergantung, maka kita memilih mereka sehingga mereka dapat dengan mudah dihitung - misalnya, kita mengambil partisi secara seragam, dan untuk titik-titik perhitungan fungsi kita mempertimbangkan opsi: 1) $$$\ xi_i = x_i$ ; 2) $$$\ xi_i = x_ {i + 1}$ ; 3) $$$\ xi_i = (x_i + x_ {i + 1}) / 2$ .

Kami mendapatkan metode persegi panjang kiri, persegi panjang kanan dan persegi panjang dengan titik tengah, masing-masing.

def _rectangle_rule(func, a, b, nseg, frac): """  .""" dx = 1.0 * (b - a) / nseg sum = 0.0 xstart = a + frac * dx # 0 <= frac <= 1    , #    , #     dx for i in range(npoints): sum += func(xstart + i * dx) return sum * dx def left_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, nseg, 0.0) def right_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, npoints, 1.0) def midpoint_rectangle_rule(func, a, b, nseg): """    """ return _rectangle_rule(func, a, b, nseg, 0.5) 

Untuk menganalisis kinerja rumus quadrature, kami membuat grafik kesalahan dalam koordinat "jumlah titik adalah perbedaan antara hasil numerik dan yang tepat."

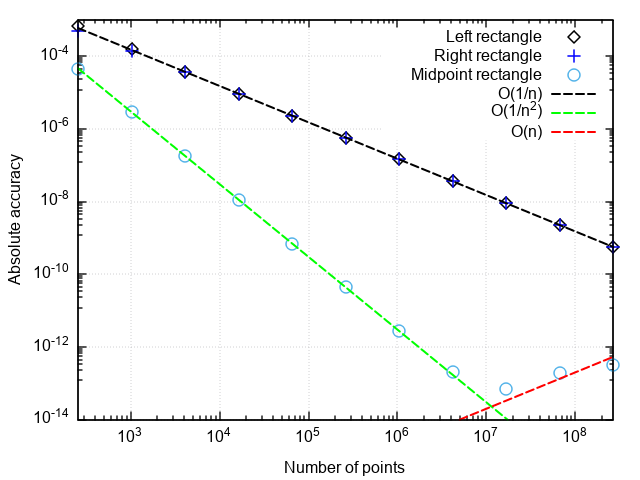
Apa yang dapat Anda perhatikan:

1. Rumus dengan titik tengah jauh lebih akurat daripada dengan titik kanan atau kiri
2. Kesalahan rumus dengan titik tengah jatuh lebih cepat daripada dua lainnya
3. Dengan partisi yang sangat kecil, kesalahan rumus dengan titik tengah mulai meningkat
   Dua poin pertama terkait dengan fakta bahwa rumus persegi panjang dengan titik tengah memiliki urutan aproksimasi kedua, yaitu $$$| I_n - I | = O (1 / n ^ 2)$ , dan rumus persegi panjang kanan dan kiri adalah urutan pertama, yaitu $$$| I_n - I | = O (1 / n)$ .
   Peningkatan kesalahan selama penggilingan langkah integrasi dikaitkan dengan peningkatan kesalahan pembulatan saat menjumlahkan sejumlah besar istilah. Kesalahan ini tumbuh seperti $$$| I_n - I | = O (1 / n)$ yang tidak memungkinkan integrasi untuk mencapai akurasi alat berat.
   Kesimpulan: metode persegi panjang dengan titik kanan dan kiri memiliki akurasi rendah, yang juga perlahan-lahan tumbuh dengan penyempurnaan partisi. Karena itu, mereka hanya masuk akal untuk tujuan demonstrasi. Metode persegi panjang dengan titik tengah memiliki urutan aproksimasi yang lebih tinggi, yang memberikannya kesempatan untuk digunakan dalam aplikasi nyata (lebih lanjut tentang itu di bawah).

Aproksimasi linear sebagian

Langkah logis berikutnya adalah memperkirakan fungsi yang dapat diintegrasikan pada masing-masing sub-segmen dengan fungsi linier, yang memberikan rumus kuadratur trapezium:

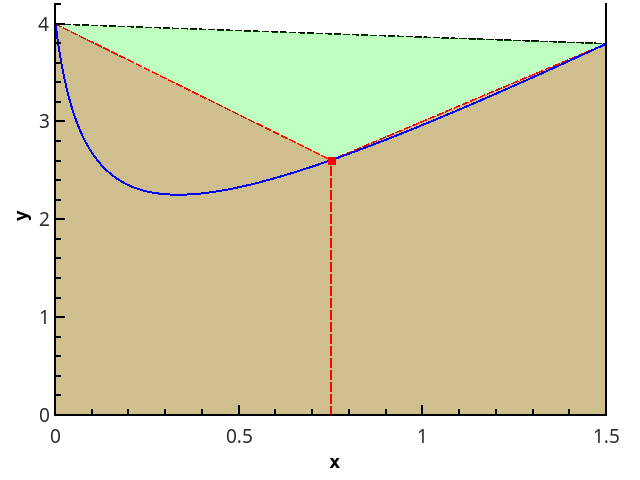
Ilustrasi metode trapesium untuk n = 1 dan n = 2.

Dalam kasus kisi yang seragam, panjang semua segmen partisi adalah sama, dan rumus memiliki bentuk

 def trapezoid_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" dx = 1.0 * (b - a) / nseg sum = 0.5 * (func(a) + func(b)) for i in range(1, nseg): sum += func(a + i * dx) return sum * dx 

Setelah memplot kesalahan dengan jumlah titik split, kita melihat bahwa metode trapesium juga memiliki urutan aproksimasi kedua dan umumnya memberikan hasil yang sedikit berbeda dari metode persegi panjang titik tengah (selanjutnya hanya metode persegi panjang).

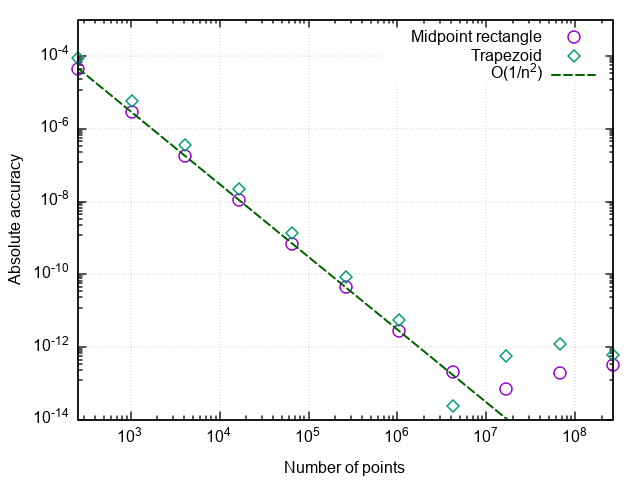
Kontrol akurasi perhitungan

Mengatur jumlah titik perpecahan sebagai parameter input tidak terlalu praktis, karena biasanya diperlukan untuk menghitung integral tidak dengan kepadatan partisi yang diberikan, tetapi dengan kesalahan yang diberikan. Jika integrand diketahui sebelumnya, maka kita dapat memperkirakan kesalahan sebelumnya dan memilih langkah integrasi sedemikian rupa sehingga akurasi yang ditentukan pasti tercapai. Tetapi ini jarang terjadi dalam praktiknya (dan secara umum, bukankah lebih mudah, dengan fungsi yang diketahui sebelumnya, untuk mengintegrasikan integral di muka?), Oleh karena itu, diperlukan prosedur untuk secara otomatis menyesuaikan langkah ke kesalahan yang diberikan.

Bagaimana cara mengimplementasikannya? Salah satu metode sederhana untuk memperkirakan kesalahan - aturan Runge - perbedaan dalam nilai integral yang dihitung dari n dan 2 n poin, memberikan perkiraan kesalahan: $$$\ Delta_ {2n} \ approx | I_ {2n} - I_n |$ . Metode trapesium lebih nyaman untuk menggandakan kehalusan partisi daripada metode persegi panjang dengan titik pusat. Saat menghitung dengan metode trapesium, untuk menggandakan jumlah poin, nilai-nilai baru dari fungsi tersebut diperlukan hanya di tengah segmen dari partisi sebelumnya, yaitu perkiraan integral sebelumnya dapat digunakan untuk menghitung berikutnya.

Dari sini kita mendapatkan kode berikut untuk metode trapesium dengan kontrol presisi:

 def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1): """  rtol -     nseg0 -    """ nseg = nseg0 old_ans = 0.0 dx = 1.0 * (b - a) / nseg ans = 0.5 * (func(a) + func(b)) for i in range(1, nseg): ans += func(a + i * dx) ans *= dx err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) #      #       nseg *= 2 err_est = abs(ans - old_ans) return ans 

Dengan pendekatan ini, integrand tidak akan dihitung beberapa kali pada satu titik, dan semua nilai yang dihitung digunakan untuk hasil akhir.

Tetapi apakah mungkin untuk mencapai akurasi yang lebih tinggi dengan jumlah perhitungan fungsi yang sama? Ternyata itu mungkin, ada rumus yang bekerja lebih akurat daripada metode trapesium pada kisi yang sama.

Aproksimasi parabola Piecewise

Langkah selanjutnya adalah memperkirakan fungsi dengan elemen parabola. Ini mensyaratkan bahwa jumlah segmen partisi menjadi genap, maka parabola dapat ditarik melalui tiga kali lipat poin dengan abscissas {( x ₀ = a , x ₁ , x ₂ ), ( x ₂ , x ₃ , x ₄ ), ..., ( x _{n -2} , x _{n -1} , x _n = b )}.

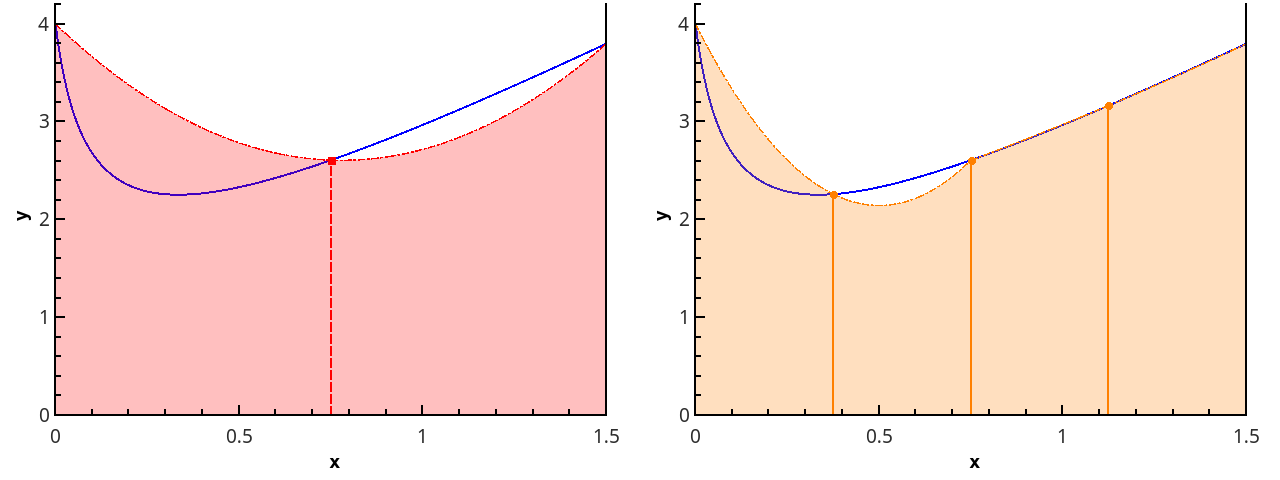
Ilustrasi pendekatan parabola piecewise pada 3 dan 5 poin ( n = 2 dan n = 3).

Mendekati integral fungsi pada masing-masing segmen [ _xk ; x _{k +2} ] oleh integral dari pendekatan parabola pada segmen ini dan dengan asumsi titik-titik akan terdistribusi secara seragam ( x _{k +1} = x _k + h ), kami memperoleh rumus Simpson :

Formula (4) secara langsung menghasilkan implementasi metode Simpson yang “naif”:

 def simpson_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" if nseg%2 = 1: nseg += 1 dx = 1.0 * (b - a) / nseg sum = (func(a) + 4 * func(a + dx) + func(b)) for i in range(1, nseg / 2): sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx) return sum * dx / 3 

Untuk memperkirakan kesalahan, Anda dapat menggunakan perhitungan integral yang sama dengan langkah h dan h / 2 - tetapi inilah masalahnya, ketika menghitung integral dengan langkah yang lebih kecil, hasil perhitungan sebelumnya harus dibuang, meskipun setengah dari perhitungan fungsi baru akan berada pada titik yang sama seperti sebelumnya.

Untungnya, Anda dapat menghindari pemborosan waktu alat berat jika Anda menerapkan metode Simpson dengan cara yang lebih cerdik. Setelah melihat lebih dekat, kami mencatat bahwa integral oleh rumus Simpson dapat diwakili melalui dua integral oleh rumus trapesium dengan langkah-langkah yang berbeda. Ini paling jelas terlihat dalam kasus dasar perkiraan integral selama tiga poin $$$(a, f_0), ~ (a + h, f_1), ~ (a + 2j, f_2)$ :

Jadi, jika kita menerapkan prosedur mengurangi langkah setengah dan menyimpan dua perhitungan terakhir dengan metode trapesium, metode Simpson dengan kontrol akurasi diimplementasikan lebih efisien.

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #           nseg0 Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ ans = Quadrature.__restart(func, x0, x1, nseg0) old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = Quadrature.__double_nseg(func, x0, x1) err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0) new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans old_trapez_sum = new_trapez_sum new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans 

Bandingkan keefektifan metode trapesium dan parabola:

 >>> import math >>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 65537 4.250000001385811 >>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 2049 4.2500000000490985 

Seperti yang Anda lihat, dengan kedua metode jawabannya dapat diperoleh dengan akurasi yang cukup tinggi, tetapi jumlah panggilan ke integrand sangat berbeda - metode urutan yang lebih tinggi 32 kali lebih efisien!

Dengan memplot kesalahan integrasi versus jumlah langkah, kita dapat memverifikasi bahwa urutan aproksimasi rumus Simpson adalah empat, yaitu kesalahan integrasi numerik $$$| I_ {Simps, n} - I | = O (1 / n ^ 4)$ (dan integral polinomial kubik menggunakan rumus ini dihitung hingga kesalahan pembulatan untuk setiap bahkan n > 0!).

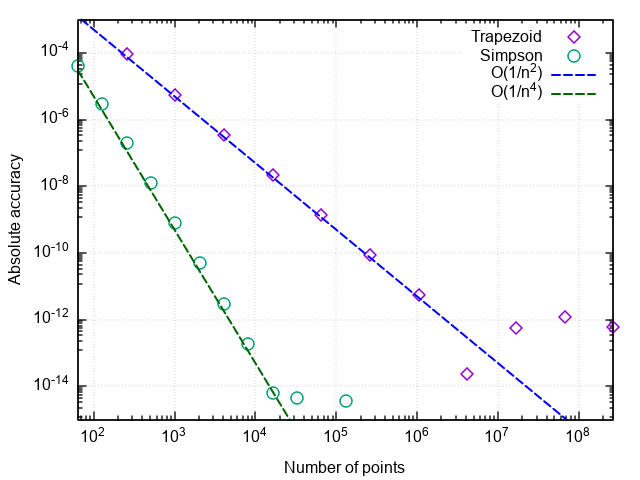
Oleh karena itu, peningkatan efisiensi tersebut muncul dibandingkan dengan formula trapesium sederhana.

Apa selanjutnya

Logika lebih lanjut untuk meningkatkan akurasi formula quadrature secara umum dapat dipahami - jika kita terus memperkirakan fungsi dengan polinomial dengan derajat yang semakin tinggi, maka integral polinomial ini akan semakin akurat memperkirakan integral dari fungsi asli. Pendekatan ini disebut konstruksi rumus Newton-Cotes kuadratik . Rumus hingga 8 perintah aproksimasi diketahui, tetapi istilah bolak-balik muncul di antara koefisien bobot w _i in (2), dan rumus kehilangan stabilitas dalam perhitungan.

Mari kita coba cara lain. Kesalahan rumus kuadratur direpresentasikan sebagai rangkaian kekuatan langkah integrasi h . Properti luar biasa dari metode trapesium (dan persegi panjang dengan titik tengah!) Apakah itu untuk seri ini hanya terdiri dari derajat genap:

Ekstrapolasi Richardson didasarkan pada penemuan perkiraan berturut-turut untuk ekspansi ini: alih-alih mendekati integrand dengan polinomial, dari perkiraan perkiraan integral $$$I (h)$ pendekatan polinomial dibangun, yang untuk h = 0 harus memberikan perkiraan terbaik dengan nilai sebenarnya dari integral.

Memperluas kesalahan integrasi bahkan dalam kekuatan langkah partisi tajam mempercepat konvergensi ekstrapolasi, karena untuk perkiraan orde 2 n , hanya nilai n integral yang diperlukan oleh metode trapesium.

Jika kita mengasumsikan bahwa setiap istilah berikutnya kurang dari yang sebelumnya, maka kita dapat secara berurutan mengecualikan derajat h , memiliki perkiraan integral yang dihitung dengan langkah-langkah yang berbeda. Karena implementasi di atas dengan mudah memungkinkan kita untuk membagi partisi menjadi dua, lebih mudah untuk mempertimbangkan rumus untuk langkah h dan h / 2.

Sangat mudah untuk menunjukkan bahwa pengecualian istilah senior kesalahan rumus trapesium akan memberikan rumus Simpson:

Mengulangi prosedur serupa untuk rumus Simpson, kita mendapatkan:

Jika Anda melanjutkan, tabel berikut ini tampak:

Kolom pertama berisi integral yang dihitung dengan metode trapesium. Ketika bergerak dari baris atas ke bawah, pembagian segmen menjadi dua kali lebih kecil, dan ketika bergerak dari kolom kiri ke kanan, urutan aproksimasi kenaikan integral (mis., Kolom kedua berisi integral dengan metode Simpson, dll.).

Elemen-elemen tabel, seperti yang dapat disimpulkan dari ekspansi (5), terkait oleh relasi perulangan:

Kesalahan perkiraan integral dapat diperkirakan dari perbedaan rumus pesanan yang berbeda dalam satu baris, yaitu

Penggunaan ekstrapolasi Richardson bersama dengan integrasi trapesium disebut metode Romberg . Jika metode Simpson memperhitungkan dua nilai sebelumnya dengan metode trapesium, metode Romberg menggunakan semua nilai yang sebelumnya dihitung oleh metode trapesium untuk mendapatkan estimasi integral yang lebih akurat.

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #          nseg0  Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True): """   nseg0 -     maxcol -   """ #   Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]] i = 0 maxcol = max(0, maxcol) ans = Itable[i][i] error_est = max(1, abs(ans)) while (error_est > abs(rtol * ans)): old_ans = ans i += 1 d = 4.0 ans_col = min(i, maxcol) Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1)) for j in range(0, ans_col): diff = Itable[i][j] - Itable[i - 1][j] Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0) d *= 4.0 ans = Itable[i][ans_col] if (maxcol <= 1): #       error_est = abs(ans - Itable[i - 1][-1]) elif (i > maxcol): error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)]) else: error_est = abs(ans - Itable[i - 1][i - 1]) print("Total function calls: " + str(Quadrature.__ncalls)) return ans 

Mari kita periksa bagaimana aproksimasi tingkat tinggi bekerja:

 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) #  Total function calls: 65537 4.250000001385811 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) #  Total function calls: 2049 4.2500000000490985 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4) Total function calls: 257 4.250000001644076 

Kami yakin bahwa, dibandingkan dengan metode parabola, jumlah panggilan ke integrand telah menurun sebanyak 8 kali. Dengan peningkatan lebih lanjut dalam akurasi yang diperlukan, keunggulan metode Romberg menjadi lebih jelas:

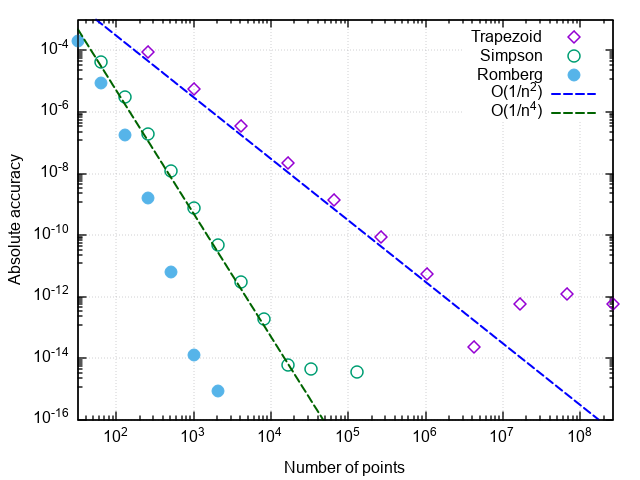
Beberapa catatan

Catatan 1. Jumlah panggilan fungsi dalam masalah ini mencirikan jumlah penjumlahan ketika menghitung integral. Mengurangi jumlah kalkulasi dari integand tidak hanya menghemat sumber daya komputasi (meskipun ini juga merupakan kasus dengan implementasi yang lebih optimal), tetapi juga mengurangi efek kesalahan pembulatan pada hasilnya. Jadi, ketika Anda mencoba menghitung integral dari fungsi tes, metode trapesium membeku ketika Anda mencoba untuk mencapai akurasi relatif 5 × 10 ^-15 , metode parabola - dengan akurasi yang diinginkan 2 × 10 ^-16 (yang merupakan batas untuk angka presisi ganda), dan metode Romberg berupaya dengan perhitungan uji integral ke akurasi mesin (dengan kesalahan bit rendah). Artinya, tidak hanya keakuratan integrasi ditingkatkan untuk sejumlah panggilan fungsi tertentu, tetapi juga keakuratan maksimum yang dapat dicapai dari perhitungan integral.

Catatan 2. Jika metode menyatu ketika akurasi tertentu ditentukan, ini tidak berarti bahwa nilai yang dihitung dari integral memiliki akurasi yang sama. Pertama-tama, ini berlaku untuk kasus-kasus ketika kesalahan yang ditentukan dekat dengan akurasi mesin.

Catatan 3. Meskipun metode Romberg untuk sejumlah fungsi bekerja dengan cara yang hampir ajaib, ia mengasumsikan bahwa integand telah membatasi turunan dari pesanan tinggi. Ini berarti bahwa untuk fungsi dengan kekusutan atau jeda, ini mungkin menjadi lebih buruk daripada metode sederhana. Misalnya, mengintegrasikan f ( x ) = | x |:

 >>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5) Total function calls: 9 5.0 >>> Quadrature.simpson(abs, -1, 3, rtol=1e-5) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3) Total function calls: 33 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4) Total function calls: 33 5.000001383269357 

Komentar 4. Tampaknya semakin tinggi urutan aproksimasi, semakin baik. Bahkan, lebih baik membatasi jumlah kolom dalam tabel Romberg menjadi 4-6. Untuk memahami ini, lihat rumus (6). Istilah kedua adalah perbedaan dari dua elemen berturut-turut dari kolom j -1 yang dibagi sekitar 4 ^j . Karena kolom j -th berisi perkiraan integral dari orde 2 j , maka perbedaannya adalah orde (1 / n _i ) ^{2 j} ~ 4 ^{- ij} . Dengan mempertimbangkan pembagian, ~ 4 ^{- ( i +1) j} ~ 4 ^{- j 2} diperoleh. Yaitu untuk j ~ 7, suku kedua dalam (6) kehilangan keakuratan setelah pengurangan pesanan ketika menambahkan angka floating-point, dan peningkatan dalam urutan aproksimasi dapat menyebabkan akumulasi kesalahan pembulatan.

Catatan 5. Pihak yang berminat dapat menggunakan metode yang dijelaskan untuk menemukan integral untuk kepentingan. $$$\ int_0 ^ 1 \ sqrt {x} \ sin {x} dx$ dan setara dengannya $$$\ int_0 ^ 1 2t ^ 2 \ sin {t ^ 2} dt$ . Seperti yang mereka katakan, rasakan perbedaannya.

Kesimpulan

Deskripsi dan implementasi metode dasar integrasi numerik fungsi pada kisi yang seragam disajikan. Hal ini menunjukkan bagaimana, menggunakan modifikasi sederhana, untuk memperoleh kelas formula quadrature menggunakan metode Romberg berdasarkan metode trapesium, yang secara signifikan mempercepat konvergensi integrasi numerik. Metode ini berfungsi dengan baik untuk mengintegrasikan fungsi "biasa", mis. lemah bervariasi pada interval integrasi, tidak memiliki singularitas di tepi segmen (lihat Komentar 5), osilasi cepat, dll.

( [3] — C++).

1. .. , .. . . .: . 1989.
2. J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
3. WH Press, SA Teukolsky, WT Vetterling, BP Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.