Kami memilih kata sandi untuk TIN India dalam dua detik, atau mengapa brute force math

Di India ada analog lokal dari INN kami - “adhar”. Sistem elektronik "eAdhar" kacau untuk itu. Di eAdhara, setiap huruf diblokir dengan kata sandi. Dan semuanya akan baik-baik saja, tetapi kata sandi dibuat berdasarkan pola sederhana: empat huruf pertama dari namanya adalah topi, ditambah tahun kelahiran.

Empat huruf besar dan empat angka. Dari jumlah tersebut, 2.821.109.909.456 kombinasi dapat dikompilasi. Jika Anda memeriksa seribu kombinasi per detik, satu kata sandi akan memakan waktu sembilan puluh tahun.

Terlalu panjang Bisakah kita mempercepat beberapa ( miliar ) kali?

92 tahun → 52 hari. Grup

Dengan tiga triliun kombinasi, kami memiliki sedikit lebih banyak. Namun, template tersebut diketahui:

([AZ][AZ][AZ][AZ]) ([0–9][0–9][0–9][0–9]) (4  ) (4 ) ( 1) ( 2) 

Dengan pola ini, garis seperti S2N65GE1 dapat langsung dibuang. Berapa banyak kombinasi yang Anda dapatkan?

Grup pertama adalah empat karakter alfabet. 26 opsi, 4 posisi, kita dapatkan:

$$

$$26 ^ 4 = $ 456 97$$

4 posisi 10 digit, serupa:

$$

$$10 ^ 4 = $ 10.00$$

Dari ini kami memperoleh jumlah total kombinasi:

$$

$$456976 × 10.000 = $ 456976000$$

Mari kita perkirakan seberapa cepat brute force sekarang. Sekali lagi, kami melanjutkan dari 1000 upaya per detik:

$$

$$456.976.000 / 1.000 = $ 4.569.76$$

Atau 52 hari, 21 jam, 22 menit, dan 40 detik. Alih-alih 92 tahun. Tidak buruk. Tapi masih lama. Apa lagi yang bisa dilakukan? Hal yang sama - kurangi jumlah kombinasi.

52 hari → 12 jam. Hidupkan akal sehat

Grup pertama dan kedua bukanlah kumpulan karakter acak, tetapi huruf pertama dari nama dan tahun kelahiran. Mari kita mulai dengan tahun kelahiran.

Tidak masuk akal untuk memilih kata sandi bagi mereka yang lahir pada tahun 1642 atau 2594. Jadi rentang kombinasi dapat dikurangi dengan aman dari 0000–9999 menjadi 1918–2018. Jadi kita akan membahas plus atau minus dari semua yang hidup pada usia 0 hingga 100 tahun. Berkat ini, jumlah kombinasi dan waktu berkurang, masing-masing:

$$

$$456.976 × 100 = $ 45.697.60$$

$$

$$45697600/1000 = $ 45697,$$

Atau 12 jam, 41 menit, dan 37 detik.

12 jam → 2 menit. Kami mengorbankan akurasi

12 jam itu hebat, tapi ... Kita harus masuk lebih dalam .

Kami sekarang memiliki 45 juta kombinasi yang secara akurat mencakup semua pengguna eAdhara. Tetapi bagaimana jika mengorbankan mereka sebagian kecil demi peningkatan kecepatan?

Kami telah menyempurnakan kombinasi digital. Surat melakukan hal serupa. Logikanya sederhana: tidak ada tahun kelahiran 9999, dan dengan cara yang sama tidak ada nama India dengan "AAAA" di awal. Tetapi bagaimana cara menentukan semua kombinasi yang cocok?

Saya mengumpulkan nama-nama India dari situs katalog, Photon banyak membantu saya dalam hal ini. Hasilnya adalah 3.283 nama unik. Tetap memangkas empat huruf pertama dan menghapus duplikat:

 grep -oP ”^\w{4}” custom.txt | sort | uniq | dd conv=ucase 

Ternyata 1.598 awalan! Ada beberapa duplikat, karena empat huruf pertama dengan nama seperti "Sanjeev" dan "Sanjit" adalah sama.

1.598 awalan - tidak cukup untuk satu setengah miliar orang? Saya setuju. Tetapi jangan lupa bahwa ini adalah awalan, bukan nama. Saya memposting daftar yang dihasilkan di Gist . Padahal, seharusnya ada lebih banyak. Anda dapat menjadi bingung, mengumpulkan 10.000 nama dari situs lain dan mendapatkan 3.000 awalan unik, tetapi saya tidak punya waktu untuk ini. Jadi kita akan mulai dari 1.598.

Mari kita hitung berapa banyak waktu yang dibutuhkan sekarang:

$$

$$1598 × 100 = $ 15980$$

$$

$$159800/1000 = $ 159,$$

Atau 2 menit dan 39,8 detik.

2 menit → 2 detik. Wikipedia untuk menyelamatkan

2 menit 40 detik adalah waktu yang diperlukan untuk memilah-milah semua kombinasi. Tetapi bagaimana jika kombinasi kesebelas benar? Atau yang terakhir? Atau yang pertama?

Sekarang daftar kombinasi diurutkan berdasarkan abjad. Tapi ini tidak ada gunanya - siapa yang mengatakan bahwa nama-nama pada "A" lebih umum daripada pada "B", atau bahwa ada lebih banyak anak berusia satu tahun daripada tujuh puluh tahun?

Penting untuk mempertimbangkan probabilitas setiap kombinasi. Di Wikipedia mereka menulis:

Di India, lebih dari 50% populasi di bawah 25 dan lebih dari 65% di bawah 35.

Berdasarkan ini, alih-alih daftar 1–100, Anda dapat mencoba ini:

 25–01 (  ,       ,     ) 25–35 36–100 

Kemudian ternyata probabilitas yang pertama $$$1598 × 25 = $ 39.95$ kombinasi meningkat hingga 50%. Kami telah memecahkan sebagian kata sandi untuk $$$39950/1000 = $ 39,9$ detik! Berikut ini $$$1598 × 10/1000 = $ 15,$ detik, kami akan mengambil 15% lagi kata sandi. Total - 65% kata sandi dalam 55,9 detik.

Sekarang untuk namanya.

Di Google, mudah untuk menemukan TOP-100 nama negara mana pun. Berdasarkan data dari India, saya memindahkan kombinasi yang sesuai ke daftar teratas. Kami berasumsi bahwa 15% populasi India memiliki nama populer. Jadi 15% dari kata sandi dapat di-crack hampir secara instan.

Hindu - 80% dari populasi India. Jadi, jika Anda memasukkan nama-nama Hindu di atas dalam daftar, itu akan mempercepat 80% upaya. Setelah langkah sebelumnya, kita pergi $$$100% - 15% = 85%$ upaya. Jika 80% dari mereka adalah nama Hindu, maka 79% (kami meninggalkan 1% untuk nama populer, tetapi bukan Hindu) kami akan memecahkan dalam 65% upaya berikutnya.

Mari kita hitung semuanya bersama-sama, dengan memperhitungkan statistik usia akun. Membagi menjadi beberapa kelompok:

 100:   { 50:  00  25  { 7:  , 43:   { 34: , 9:   } } 15:  26  35  { 3:  , 13*:   { 10: , 3:   } } 45:  36  100  { 7:  , 38:   { 30: , 8:   } } } 

Sekarang mari kita buat algoritma yang efisien untuk meretas kata sandi:

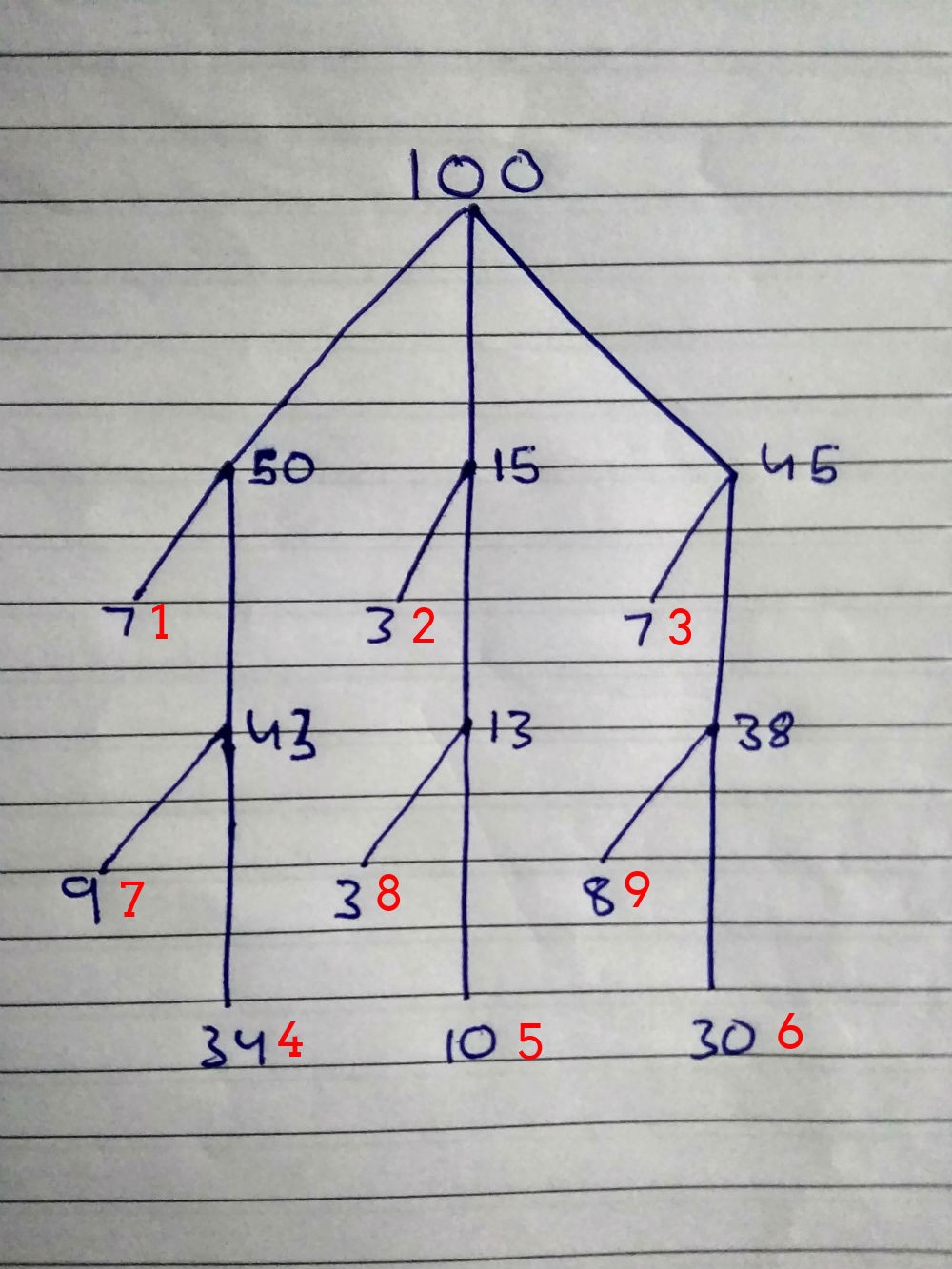
Angka merah adalah prioritas pencarian. Kombinasi untuk orang-orang dari kelompok pertama diuji terlebih dahulu, lalu kedua, lalu ketiga dan seterusnya.

Berapa lama waktu yang dibutuhkan untuk meretas sekarang?

Fase 1
1 = 11 detik untuk memecahkan 7 kata sandi
2 = 3 detik untuk memecahkan 3 kata sandi
3 = 11 detik untuk memecahkan 7 kata sandi

Kami memecahkan kata sandi 17 orang, 83 tetap. Kami akan menghapus kombinasi sebelumnya dari daftar dan akan mencoba set berikut - 4, 5, 6.

Fase 2
4 = 54 detik untuk memecahkan 34 kata sandi
5 = 16 detik untuk memecahkan 10 kata sandi
6 = 47 detik untuk memecahkan 30 kata sandi

Sekali lagi, hapus kombinasi dari fase sebelumnya.

Fase 3
7 = 14 detik untuk memecahkan 9 kata sandi
8 = 5 detik untuk memecahkan 3 kata sandi
9 = 12 detik untuk memecahkan 8 kata sandi

Total waktu : $$$11 + 3 + 11 + 54 + 16 + 47 + 14 + 5 + 12 = $ 17$ detik atau 2 menit dan 13 detik.

Kata sandi retak : 100

Waktu rata-rata untuk satu kata sandi : $$$173/100 = $ 1,7$ detik.

92 tahun → 1,73 detik. Nitsche begitu, kan?