Metode universal untuk menyortir informasi kompleks ditemukan

Membuka kafe Anda, Anda ingin tahu jawaban atas pertanyaan berikut: "di mana kafe lain yang paling dekat dengan titik ini?" Informasi ini akan membantu Anda lebih memahami pesaing Anda.

Ini adalah contoh masalah pencarian " tetangga terdekat ", yang banyak dipelajari dalam ilmu komputer. Diberikan seperangkat informasi dan titik baru, dan Anda perlu menemukan ke titik mana dari yang sudah ada itu akan terdekat? Pertanyaan seperti itu muncul dalam banyak situasi sehari-hari di berbagai bidang seperti penelitian genom, pencarian gambar, dan rekomendasi Spotify.

Tapi, tidak seperti contoh kafe, pertanyaan tentang tetangga terdekat seringkali sangat rumit. Selama beberapa dekade terakhir, pikiran terbesar di antara para ilmuwan komputer telah mengatur tentang menemukan cara terbaik untuk menyelesaikan masalah ini. Secara khusus, mereka mencoba untuk mengatasi komplikasi yang timbul dari fakta bahwa dalam set data yang berbeda akan ada definisi yang sangat berbeda dari "kedekatan" satu sama lain.

Dan sekarang, tim ilmuwan komputer telah menemukan cara yang sama sekali baru untuk menyelesaikan masalah menemukan tetangga terdekat. Dalam sepasang makalah, lima ilmuwan menggambarkan secara rinci metode umum pertama untuk memecahkan masalah menemukan tetangga terdekat untuk data yang kompleks.

"Ini adalah hasil pertama yang menjangkau berbagai ruang menggunakan teknik algoritme tunggal," kata Peter Indik , seorang spesialis IT di Massachusetts Institute of Technology, seorang tokoh berpengaruh di bidang pengembangan yang terkait dengan tugas ini.

Perbedaan jarak

Kami sangat terikat pada satu-satunya cara untuk menentukan jarak sehingga mudah untuk melupakan kemungkinan cara lain. Biasanya kita mengukur jarak sebagai Euclidean - sebagai garis lurus antara dua titik. Namun, ada situasi di mana definisi lain lebih masuk akal. Misalnya, jarak Manhattan membuat Anda berputar 90 derajat, seolah bergerak di sepanjang jaringan jalan persegi panjang. Untuk mengukur jarak yang mungkin 5 kilometer dalam garis lurus, Anda mungkin perlu melintasi kota 3 km dalam satu arah dan kemudian 4 lagi di yang lain.

Dimungkinkan juga untuk membicarakan jarak yang tidak dalam arti geografis. Berapa jarak antara dua orang di jejaring sosial, atau dua film, atau dua genom? Dalam contoh-contoh ini, jarak menunjukkan tingkat kesamaan.

Ada puluhan metrik jarak, yang masing-masing cocok untuk tugas tertentu. Ambil, misalnya, dua genom. Ahli biologi membandingkannya menggunakan " jarak Levenshtein " atau jarak pengeditan. Jarak pengeditan antara dua sekuens genom adalah jumlah penambahan, penghapusan, penyisipan dan penggantian yang diperlukan untuk mengubah salah satu dari mereka menjadi yang lain.

Mengedit jarak dan jarak Euclidean adalah dua konsep jarak yang berbeda, dan tidak mungkin untuk mengurangi satu ke yang lain. Ketidakcocokan ini ada untuk banyak pasangan metrik jarak, dan merupakan hambatan bagi para ilmuwan komputer yang mencoba mengembangkan algoritma untuk menemukan tetangga terdekat. Ini berarti bahwa suatu algoritma yang bekerja untuk satu jenis jarak tidak akan bekerja untuk yang lain - lebih tepatnya, sampai sekarang, sampai jenis pencarian baru muncul.


Alexander Andoni

Lingkaran kuadrat

Pendekatan standar untuk menemukan tetangga terdekat adalah dengan membagi data yang ada menjadi subkelompok. Jika, misalnya, data Anda menggambarkan lokasi sapi di padang rumput, maka Anda dapat melampirkan masing-masing dalam lingkaran. Lalu kami meletakkan sapi baru di padang rumput dan mengajukan pertanyaan: di lingkaran manakah itu? Secara praktis dijamin bahwa tetangga terdekat sapi baru akan berada dalam lingkaran yang sama.

Kemudian ulangi prosesnya. Bagilah lingkaran menjadi sub-lingkaran, bagilah sel-sel ini lebih jauh, dan seterusnya. Akibatnya, ada sel dengan hanya dua titik: yang ada dan yang baru. Titik yang ada ini akan menjadi tetangga terdekat Anda.


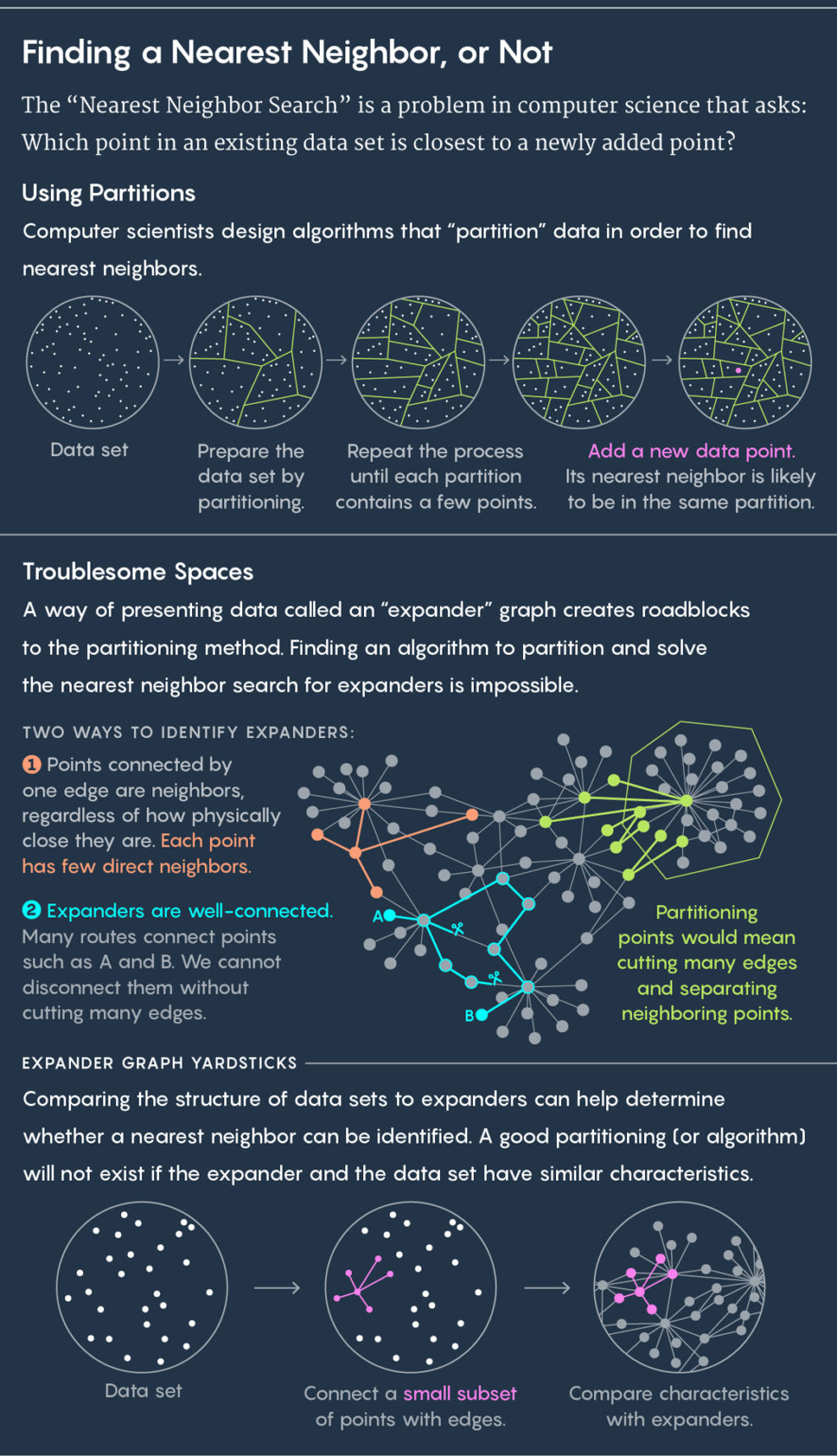Di atas adalah pembagian data menjadi sel. Di bawah ini adalah penggunaan grafik ekstensi.

Algoritma menggambar sel, algoritma yang baik menggambarnya dengan cepat dan baik - yaitu, sehingga tidak ada situasi di mana sapi baru jatuh ke dalam lingkaran dan tetangga terdekatnya berakhir di lingkaran lain. "Kami ingin titik-titik dekat di sel-sel ini muncul lebih sering dalam drive yang sama satu sama lain, dan yang jauh menjadi langka," kata Ilya Razenshtein , spesialis ilmu komputer di Microsoft Research, rekan penulis karya baru, yang juga melibatkan Alexander Andoni dari Universitas Columbia. , Assaf Naor dari Princeton, Alexander Nikolov dari Universitas Toronto, dan Eric Weingarten dari Universitas Columbia.

Selama bertahun-tahun, para ilmuwan komputer telah menemukan berbagai algoritma untuk menggambar sel-sel tersebut. Untuk data kecil - seperti ketika satu titik ditentukan oleh sejumlah kecil nilai, misalnya, lokasi sapi di padang rumput - algoritma membuat apa yang disebut " Diagram Voronoi " yang secara akurat menjawab pertanyaan tentang tetangga terdekat.

Untuk data multidimensi, di mana satu titik dapat ditentukan oleh ratusan atau ribuan nilai, diagram Voronoi membutuhkan daya komputasi terlalu banyak. Alih-alih, programmer menggambar sel menggunakan " hashing sensitif lokal, " pertama kali dijelaskan oleh Indik dan Rajiv Motwani pada tahun 1998. Algoritma LF menggambar sel secara acak. Oleh karena itu, mereka bekerja lebih cepat, tetapi kurang akurat - alih-alih menemukan tetangga terdekat yang tepat, mereka menjamin bahwa suatu titik terletak tidak lebih dari jarak yang diberikan dari tetangga terdekat yang sebenarnya. Ini bisa dibayangkan sebagai rekomendasi film Netflix, yang tidak sempurna, tetapi cukup baik.

Sejak akhir 1990-an, para ilmuwan komputer telah membuat algoritma LF yang memberikan solusi perkiraan untuk tugas menemukan tetangga terdekat untuk metrik jarak yang diberikan. Algoritma sangat khusus, dan algoritma yang dikembangkan untuk satu metrik jarak tidak dapat digunakan untuk yang lain.

“Anda dapat menemukan algoritma yang sangat efektif untuk jarak Euclidean atau Manhattan, untuk beberapa kasus tertentu. Tetapi kami tidak memiliki algoritma yang bekerja pada kelas jarak yang besar, "kata Indik.

Karena algoritma yang bekerja dengan satu metrik tidak dapat digunakan untuk yang lain, pemrogram membuat strategi penyelesaian masalah. Melalui proses yang disebut "embedding," mereka memberlakukan metrik, di mana mereka tidak memiliki algoritma yang baik, pada metrik untuk mana itu. Namun, korespondensi metrik biasanya tidak akurat - sesuatu seperti pasak persegi di lubang bundar. Dalam beberapa kasus, penyematan tidak berhasil sama sekali. Itu perlu untuk datang dengan cara universal untuk menjawab pertanyaan tentang tetangga terdekat.


Ilya Razenshtein

Hasil yang tidak terduga

Dalam sebuah karya baru, para ilmuwan meninggalkan pencarian untuk algoritma khusus. Sebaliknya, mereka mengajukan pertanyaan yang lebih luas: apa yang mencegah pengembangan suatu algoritma pada metrik jarak tertentu?

Mereka memutuskan bahwa situasi yang tidak menyenangkan terkait dengan grafik yang berkembang, atau expander , yang harus disalahkan. Expander adalah jenis grafik khusus, sekumpulan titik yang dihubungkan oleh tepian. Grafik memiliki metrik jarak sendiri. Jarak antara dua titik grafik adalah jumlah minimum garis yang diperlukan untuk berpindah dari satu titik ke titik lainnya. Anda dapat membayangkan grafik yang mewakili koneksi antara orang-orang di jejaring sosial, dan kemudian jarak antara orang-orang akan sama dengan jumlah koneksi yang memisahkan mereka. Jika, misalnya, Julian Moore memiliki teman yang memiliki teman yang memiliki Kevin Bacon sebagai temannya, maka jarak dari Moore ke Bacon adalah tiga.

Ekspander adalah jenis grafik khusus yang memiliki dua, pada pandangan pertama, properti yang saling bertentangan. Ini memiliki konektivitas tinggi, yaitu, dua titik tidak dapat terputus tanpa memotong beberapa sisi. Pada saat yang sama, sebagian besar titik terhubung ke jumlah yang sangat kecil. Karena itu, sebagian besar poin jauh dari satu sama lain.

Kombinasi unik dari properti ini - konektivitas yang baik dan sejumlah kecil tepi - mengarah pada fakta bahwa pada ekspander tidak mungkin untuk melakukan pencarian cepat untuk tetangga terdekat. Setiap upaya untuk membaginya menjadi sel akan memisahkan titik-titik yang letaknya berdekatan satu sama lain.

"Cara apa pun untuk memotong expander menjadi dua bagian membutuhkan memotong beberapa tulang rusuk, yang membagi banyak simpul yang berjarak dekat," kata Weingarten, penulis pendamping penelitian ini.

Pada musim panas 2016, Andoni, Nyokolov, Rasenstein dan Vanguarten tahu bahwa untuk ekspander seseorang tidak dapat menemukan algoritma yang baik untuk menemukan tetangga terdekat. Tetapi mereka ingin membuktikan bahwa tidak mungkin untuk membangun algoritma seperti itu untuk banyak metrik jarak lainnya - metrik, ketika mencari algoritma yang baik yang mana para ilmuwan komputer terhenti.

Untuk menemukan bukti ketidakmungkinan algoritma seperti itu, mereka perlu menemukan cara untuk menanamkan metrik expander di metrik jarak lain. Dengan metode ini, mereka dapat menentukan bahwa metrik lain memiliki properti yang mirip dengan properti expander, yang mencegah mereka membuat algoritma yang baik.


Eric Weingarten

Empat ilmuwan komputer pergi ke Assaf Naoru, seorang ahli matematika dari Universitas Princeton, yang karyanya sebelumnya sangat cocok dengan topik ekspander. Mereka memintanya untuk membantu membuktikan bahwa ekspander dapat disematkan dalam berbagai jenis metrik. Naor cepat kembali dengan jawaban - tetapi bukan jawaban yang mereka harapkan darinya.

"Kami meminta Assaf untuk membantu kami dengan pernyataan ini, dan dia membuktikan sebaliknya," kata Andoni.

Naor membuktikan bahwa ekspander tidak masuk dalam kelas besar metrik jarak yang dikenal sebagai " ruang bernorma " (yang juga mencakup metrik seperti ruang Euclidean dan Manhattan). Berdasarkan bukti Naor, para ilmuwan mengikuti rantai logis berikut: jika ekspander tidak sesuai dengan metrik jarak, maka harus ada cara yang baik untuk memecahnya menjadi sel (karena, sebagaimana terbukti, sifat ekspander adalah satu-satunya penghalang untuk ini). Karena itu, harus ada algoritma yang baik untuk menemukan tetangga terdekat - bahkan jika belum ada yang menemukannya.

Lima peneliti menerbitkan temuan mereka di sebuah makalah yang mereka selesaikan pada bulan November dan diunggah pada bulan April. Itu diikuti oleh karya kedua, yang mereka selesaikan tahun ini dan diterbitkan pada bulan Agustus. Di dalamnya, mereka menggunakan informasi yang diperoleh saat menulis karya pertama untuk menemukan algoritma cepat untuk menemukan tetangga terdekat untuk ruang bernorma.

"Pekerjaan pertama menunjukkan adanya cara untuk memecah metrik menjadi dua bagian, tetapi tidak ada resep untuk melakukannya dengan cepat," kata Weingarten. "Dalam karya kedua, kami berpendapat bahwa ada cara untuk memisahkan poin, dan di samping itu, pemisahan ini dapat dilakukan dengan menggunakan algoritma cepat."

Akibatnya, karya-karya baru untuk pertama kalinya menggeneralisasi pencarian tetangga terdekat dalam data multidimensi. Alih-alih mengembangkan algoritma khusus untuk metrik tertentu, programmer memiliki pendekatan universal untuk menemukan algoritma.

"Ini adalah metode tertib untuk mengembangkan algoritma untuk menemukan tetangga terdekat di salah satu metrik jarak yang Anda butuhkan," kata Weingarten.