Saya berjuang dengan godaan untuk menyebut artikel itu sesuatu seperti "Inefisiensi mengerikan dari algoritma STL" - Anda tahu, hanya demi pelatihan dalam seni menciptakan berita utama yang mencolok. Namun demikian, ia memutuskan untuk tetap dalam batas kesusilaan - lebih baik untuk mendapatkan komentar dari pembaca tentang isi artikel daripada kemarahan karena nama besarnya.
Pada titik ini saya akan berasumsi bahwa Anda tahu sedikit C ++ dan STL, dan juga mengurus algoritma yang digunakan dalam kode Anda, kompleksitas dan relevansinya dengan tugas-tugas.
Algoritma
Salah satu kiat terkenal yang dapat Anda dengar dari komunitas pengembang C ++ modern adalah tidak menggunakan sepeda, tetapi menggunakan algoritma dari perpustakaan standar. Ini saran yang bagus. Algoritma ini aman, cepat, diuji selama bertahun-tahun. Saya juga sering memberi saran untuk menerapkannya.
Setiap kali Anda ingin menulis yang lain untuk - Anda harus terlebih dahulu ingat jika ada sesuatu di STL (atau dorongan) yang sudah memecahkan masalah ini dalam satu baris. Jika ada, sering kali lebih baik menggunakan ini. Namun, dalam hal ini, kita juga harus memahami jenis algoritma apa yang ada di balik pemanggilan fungsi standar, apa karakteristik dan batasannya.
Biasanya, jika masalah kita sama persis dengan deskripsi algoritma dari STL, itu akan menjadi ide yang baik untuk mengambil dan menerapkannya "dahi". Satu-satunya masalah adalah bahwa data tidak selalu disimpan dalam bentuk di mana algoritma yang diterapkan di perpustakaan standar ingin menerimanya. Maka kita mungkin memiliki ide untuk mengkonversi data terlebih dahulu, dan kemudian masih menerapkan algoritma yang sama. Ya, Anda tahu, seperti dalam lelucon matematika itu, “Matikan api dari ketel. Tugas dikurangi menjadi yang sebelumnya. "
Persimpangan set
Bayangkan kita sedang mencoba untuk menulis alat untuk programmer C ++ yang akan menemukan semua lambda dalam kode dengan menangkap semua variabel default ([=] dan [&]) dan menampilkan tips untuk mengubahnya menjadi lambdas dengan daftar spesifik variabel yang ditangkap. Sesuatu seperti ini:
std::partition(begin(elements), end(elements), [=] (auto element) {
Dalam proses parsing file dengan kode, kita harus menyimpan koleksi variabel di suatu tempat dalam lingkup saat ini dan sekitarnya, dan jika lambda terdeteksi dengan penangkapan semua variabel, bandingkan dua koleksi ini dan berikan saran tentang konversi.
Satu set dengan variabel dalam lingkup induk, dan satu lagi dengan variabel di dalam lambda. Untuk membentuk saran, pengembang hanya perlu menemukan persimpangan mereka. Dan ini adalah kasus ketika deskripsi algoritma dari STL sangat cocok untuk tugas:
std :: set_intersection mengambil dua set dan mengembalikan persimpangan mereka. Algoritma itu indah dalam kesederhanaannya. Dibutuhkan dua koleksi yang diurutkan dan dijalankan secara paralel:
- Jika item saat ini di koleksi pertama identik dengan item saat ini di koleksi kedua - tambahkan ke hasilnya dan pindah ke item berikutnya di kedua koleksi
- Jika item saat ini di koleksi pertama kurang dari item saat ini di koleksi kedua, buka item berikutnya di koleksi pertama
- Jika item saat ini di koleksi pertama lebih besar dari item saat ini di koleksi kedua, pergi ke item berikutnya di koleksi kedua
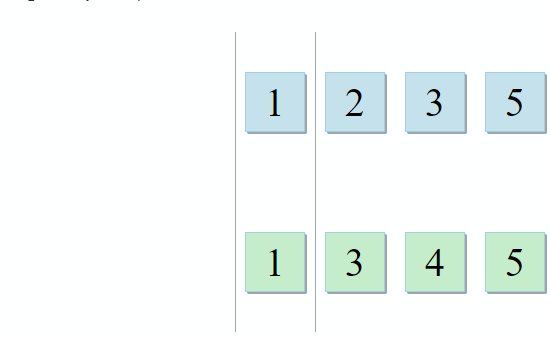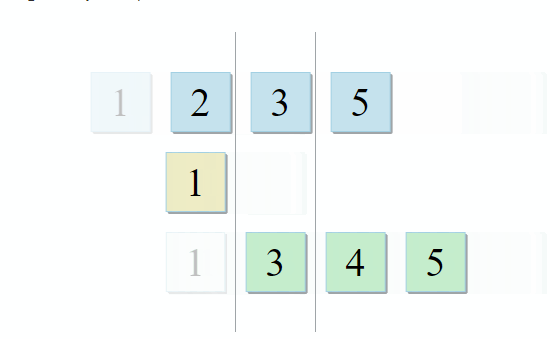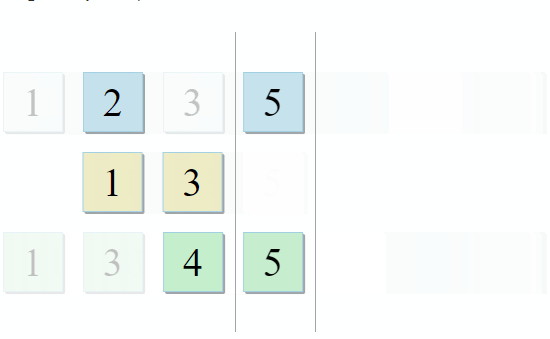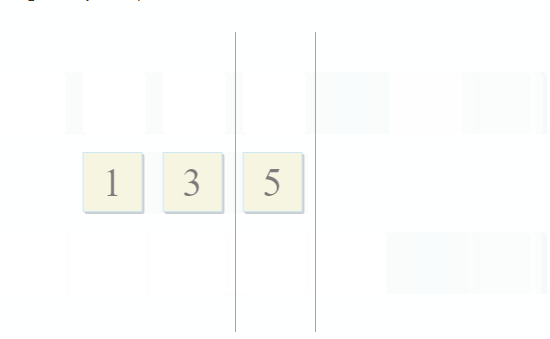
Dengan setiap langkah algoritma, kami bergerak di sepanjang koleksi pertama, kedua, atau keduanya, yang berarti bahwa kompleksitas algoritma ini akan linier - O (m + n), di mana n dan m adalah ukuran koleksi.
Sederhana dan efektif. Tapi ini hanya sejauh koleksi input diurutkan.
Menyortir
Masalahnya adalah bahwa, secara umum, koleksi tidak diurutkan. Dalam kasus khusus kami, akan lebih mudah untuk menyimpan variabel dalam beberapa struktur data seperti tumpukan dengan menambahkan variabel ke tingkat tumpukan berikutnya ketika memasukkan lingkup bersarang dan menghapusnya dari tumpukan ketika meninggalkan ruang lingkup ini.
Ini berarti bahwa variabel tidak akan diurutkan berdasarkan nama dan kami tidak dapat langsung menggunakan std :: set_intersection pada koleksi mereka. Karena std :: set_intersection membutuhkan koleksi yang diurutkan secara tepat pada input, idenya mungkin muncul (dan saya sering melihat pendekatan ini dalam proyek nyata) untuk mengurutkan koleksi sebelum memanggil fungsi perpustakaan.
Menyortir dalam kasus ini akan mematikan seluruh gagasan menggunakan stack untuk menyimpan variabel sesuai dengan cakupannya, tetapi tetap saja ini mungkin:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_1(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { std::sort(first1, last1); std::sort(first2, last2); return std::set_intersection(first1, last1, first2, last2, dest); }
Apa kompleksitas dari algoritma yang dihasilkan? Sesuatu seperti O (n log n + m log m + n + m) adalah kompleksitas quasilinear.
Lebih sedikit penyortiran
Bisakah kita tidak menggunakan penyortiran? Kita bisa, mengapa tidak. Kami hanya akan mencari setiap elemen dari koleksi pertama dalam pencarian linear kedua. Kami mendapatkan kompleksitas O (n * m). Dan saya juga sering melihat pendekatan ini dalam proyek nyata.
Alih-alih opsi "urutkan semuanya" dan "jangan urutkan apa pun", kita dapat mencoba menemukan Zen dan melakukan cara ketiga - hanya mengurutkan salah satu koleksi. Jika salah satu koleksi diurutkan, tetapi yang kedua tidak, maka kita dapat mengulangi elemen koleksi yang tidak disortir satu per satu dan mencari mereka di pencarian biner yang disortir.
Kompleksitas dari algoritma ini adalah O (n log n) untuk menyortir koleksi pertama dan O (m log n) untuk mencari dan memeriksa. Secara total, kami mendapatkan kompleksitas O ((n + m) log n).
Jika kami memutuskan untuk menyortir koleksi lain, kami mendapatkan kompleksitas O ((n + m) log m). Seperti yang Anda pahami, akan logis untuk menyortir koleksi yang lebih kecil di sini untuk mendapatkan kompleksitas akhir log O ((m + n) (min (m, n))
Implementasinya akan terlihat seperti ini:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_2(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_2(first2, last2, first1, last1, dest); return; } std::sort(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return std::binary_search(first1, last1, FWD(value)); }); }
Dalam contoh kami dengan fungsi lambda dan menangkap variabel, koleksi yang akan kami sortir biasanya akan menjadi kumpulan variabel yang digunakan dalam kode fungsi lambda, karena ada kemungkinan lebih sedikit variabel daripada variabel dalam lingkup lambda sekitarnya.
Hashing
Dan opsi terakhir yang dibahas dalam artikel ini adalah menggunakan hashing untuk koleksi yang lebih kecil daripada menyortirnya. Ini akan memberi kita kesempatan untuk mencari O (1) di dalamnya, meskipun pembangunan hash, tentu saja, akan memakan waktu (dari O (n) hingga O (n * n), yang dapat menjadi masalah):
template <typename InputIt1, typename InputIt2, typename OutputIt> void unordered_intersection_3(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_3(first2, last2, first1, last1, dest); return; } std::unordered_set<int> test_set(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return test_set.count(FWD(value)); }); }
Pendekatan hashing akan menjadi pemenang mutlak ketika tugas kita adalah untuk secara konsisten membandingkan beberapa set kecil A dengan set set B₁, B₂, B .... Dalam hal ini, kita perlu membuat hash untuk A hanya sekali, dan kita dapat menggunakan pencarian instan untuk membandingkannya dengan elemen-elemen dari semua set B yang sedang dipertimbangkan.
Tes kinerja
Itu selalu berguna untuk mengkonfirmasi teori dengan praktek (terutama dalam kasus-kasus seperti yang terakhir, ketika tidak jelas apakah biaya awal hashing akan terbayar dengan keuntungan dalam kinerja pencarian).
Dalam pengujian saya, opsi pertama (dengan mengurutkan kedua koleksi) selalu menunjukkan hasil terburuk. Menyortir hanya satu koleksi kecil bekerja sedikit lebih baik pada koleksi dengan ukuran yang sama, tetapi tidak terlalu banyak. Tetapi algoritma kedua dan ketiga menunjukkan peningkatan yang sangat signifikan dalam produktivitas (sekitar 6 kali) dalam kasus di mana salah satu koleksi 1000 kali lebih besar dari yang lain.