Geekly articles weekly

Sortir berdasarkan pilihan



Apa ide menyortir berdasarkan pilihan?

  1. Dalam subarray yang tidak disortir, maksimum lokal (minimum) dicari.
  2. Maksimum (minimum) yang ditemukan mengubah tempat-tempat dengan elemen (pertama) terakhir dalam subarray.
  3. Jika subarrays yang tidak disortir tetap ada dalam array, lihat poin 1.

Penyimpangan liris sedikit. Awalnya, dalam seri artikel saya, saya berencana untuk secara konsisten menyajikan materi tentang penyortiran kelas dalam urutan yang ketat. Setelah pemilahan perpustakaan , artikel tentang algoritma penyisipan lainnya direncanakan: pengurutan solitaire, pengurutan berdasarkan tabel Young, pengurutan menurut inversi, dll.

Namun, sekarang trennya adalah nonlinier, oleh karena itu, tanpa menulis semua publikasi tentang penyortiran menurut sisipan, hari ini saya akan memulai cabang paralel tentang penyortiran berdasarkan pilihan. Kemudian saya akan melakukan hal yang sama untuk kelas algoritmik lainnya: menggabungkan jenis, jenis distribusi, dll. Ini umumnya akan memungkinkan publikasi untuk ditulis pada satu topik, kemudian pada yang lain. Dengan rotasi tematik seperti itu akan lebih menyenangkan.

Sortir seleksi




Sederhana dan bersahaja - kita menelusuri array untuk mencari elemen maksimum. Maksimum yang ditemukan dipertukarkan dengan elemen terakhir. Bagian array yang tidak disortir berkurang satu elemen (tidak termasuk elemen terakhir tempat kami menyusun ulang maksimum yang ditemukan). Kami menerapkan tindakan yang sama untuk bagian yang tidak disortir ini - kami menemukan maksimum dan meletakkannya di tempat terakhir di bagian yang tidak disortir dari array. Jadi kami melanjutkan hingga bagian array yang tidak disortir dikurangi menjadi satu elemen.

def selection(data): for i, e in enumerate(data): mn = min(range(i, len(data)), key=data.__getitem__) data[i], data[mn] = data[mn], e return data


Menyortir dengan pilihan sederhana adalah pencarian ganda kasar. Bisakah ini diperbaiki? Mari kita lihat beberapa modifikasi.

Sortir pilihan ganda :: Sortir pilihan ganda




Gagasan serupa digunakan dalam penyortiran shaker , yang merupakan varian dari penyortiran gelembung. Melewati bagian array yang tidak disortir, selain maksimum, kami juga secara bersamaan menemukan minimum. Kami menempatkan minimum di tempat pertama, maksimum di yang terakhir. Dengan demikian, bagian yang tidak disortir pada setiap iterasi dikurangi oleh dua elemen sekaligus.

Sepintas, tampaknya ini mempercepat algoritme sebanyak 2 kali - setelah setiap lintasan, subarray yang tidak disortir dikurangi bukan dari satu, tetapi dari dua sisi sekaligus. Tetapi pada saat yang sama, jumlah perbandingan meningkat 2 kali, dan jumlah swap tetap tidak berubah. Pilihan ganda hanya sedikit meningkatkan kecepatan algoritme, dan dalam beberapa bahasa bahkan bekerja lebih lambat karena alasan tertentu.

Perbedaan antara penyortiran berdasarkan pilihan dari penyortiran penyisipan


Tampaknya menyortir berdasarkan pilihan dan menyortir berdasarkan sisipan adalah satu dan hal yang sama, kelas umum dari algoritma. Nah, atau menyortir berdasarkan sisipan adalah semacam penyortiran berdasarkan pilihan. Atau mengurutkan berdasarkan pilihan adalah kasus khusus pengurutan berdasarkan sisipan. Dan di sana-sini, kita bergiliran dari bagian array yang tidak disortir untuk mengekstrak elemen dan mengarahkannya ke area yang diurutkan.

Perbedaan utama: dalam mengurutkan berdasarkan sisipan, kami mengekstrak elemen apa pun dari bagian array yang tidak disortir dan memasukkannya ke tempatnya di bagian yang diurutkan. Dalam pemilihan sortir, kami sengaja mencari elemen maksimum (atau minimum) yang dengannya kami melengkapi bagian yang diurutkan dari array. Di insets kita mencari di mana untuk memasukkan elemen berikutnya, dan dalam pilihan - kita sudah tahu sebelumnya tempat apa yang akan kita taruh, tetapi pada saat yang sama kita perlu menemukan elemen yang sesuai dengan tempat ini.

Ini membuat kedua kelas algoritma sangat berbeda satu sama lain dalam esensinya dan metode yang digunakan.

Bingo sort :: Bingo sort


Fitur yang menarik dari pilihan pengurutan adalah kecepatan kemandirian dari sifat data yang disortir.

Misalnya, jika array hampir diurutkan, maka, seperti yang Anda tahu, menyortir menurut sisipan akan memprosesnya lebih cepat (bahkan lebih cepat daripada penyortiran cepat). Array dengan urutan terbalik untuk menyortir menurut sisipan adalah kasus yang merosot, ia akan mengurutkannya selama mungkin.

Dan untuk mengurutkan berdasarkan pilihan, pemesanan sebagian atau terbalik dari array tidak memainkan peran - itu akan memprosesnya dengan kecepatan yang sama dengan yang acak acak. Selain itu, untuk penyortiran klasik, tidak masalah jika array terdiri dari elemen unik atau berulang - ini praktis tidak mempengaruhi kecepatan.

Namun pada prinsipnya, Anda bisa membuat dan memodifikasi algoritma sehingga itu bekerja lebih cepat dengan beberapa set data. Misalnya, penyortiran bingo memperhitungkan jika array terdiri dari elemen berulang.



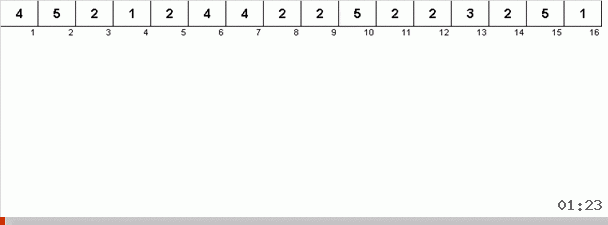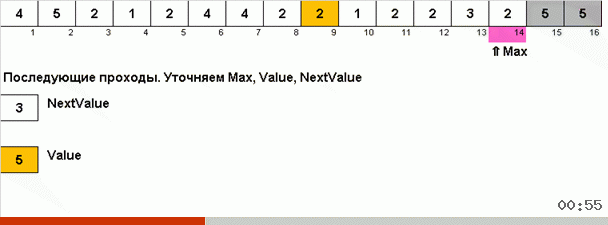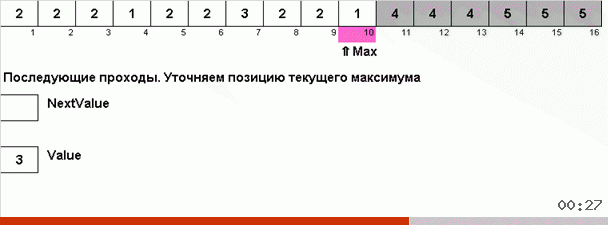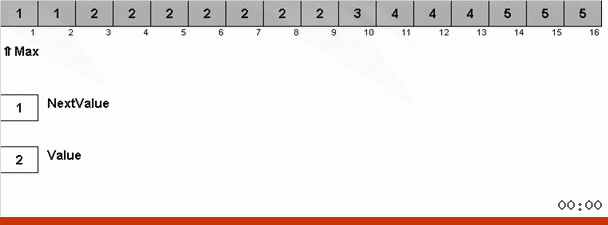
Kuncinya di sini adalah bahwa tidak hanya elemen maksimum yang diingat di bagian yang berantakan, tetapi juga maksimum untuk iterasi berikutnya ditentukan. Hal ini memungkinkan untuk berulang maksimum tidak untuk mencari mereka lagi setiap kali, tetapi menempatkan mereka di tempat mereka segera setelah maksimum ini sekali lagi ditemui dalam array.

Kompleksitas algoritmik tetap sama. Tetapi jika array terdiri dari angka berulang, maka pengurutan bingo akan mengatasi sepuluh kali lebih cepat daripada pengurutan menurut pilihan biasa.

 # - def bingo(data): #  . max = len(data) - 1 nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 #  . while max: value = nextValue nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] == value: data[i], data[max] = data[max], data[i] max -= 1 elif data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 return data


Sortir siklus :: Sortir siklus


Penyortiran loop menarik (dan berharga dari sudut pandang praktis) karena perubahan di antara elemen array terjadi jika dan hanya jika elemen diletakkan di tempat terakhirnya. Ini bisa berguna jika menulis ulang dalam array terlalu mahal dan merawat memori fisik membutuhkan meminimalkan jumlah perubahan pada elemen array.



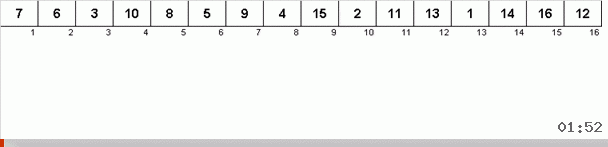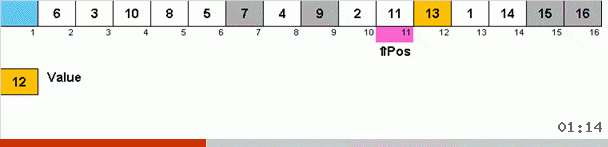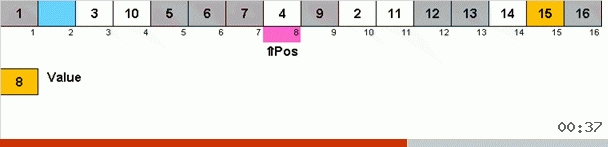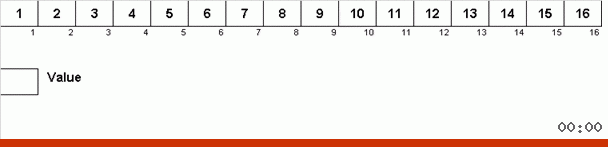
Ini berfungsi seperti ini. Kami menyortir array, memanggil X sel berikutnya di lingkaran luar ini. Dan kita melihat tempat apa dalam array yang kita butuhkan untuk memasukkan elemen selanjutnya dari sel ini. Di tempat Anda ingin menempelkan beberapa elemen lain, kami mengirimkannya ke clipboard. Untuk elemen ini di buffer, kami juga mencari tempatnya di array (dan menempelkannya ke tempat ini, dan mengirim ke buffer elemen yang muncul di tempat ini). Dan untuk nomor baru di buffer, kami melakukan tindakan yang sama. Berapa lama proses ini harus dilanjutkan? Hingga elemen berikutnya di clipboard ternyata menjadi elemen yang perlu dimasukkan secara tepat di sel X (tempat saat ini dalam array di loop utama algoritma). Cepat atau lambat momen ini akan terjadi dan kemudian di lingkaran luar Anda dapat pergi ke sel berikutnya dan ulangi prosedur yang sama untuk itu.

Dalam jenis lain, berdasarkan pilihan, kami mencari maksimum / minimum untuk menempatkan mereka di tempat terakhir / pertama. Dalam sortir siklus, ternyata setidaknya tempat pertama dalam subarray berada, seolah-olah, dalam proses bagaimana beberapa elemen lain diletakkan di tempat yang selayaknya di suatu tempat di tengah array.

Dan di sini, kompleksitas algoritmik juga tetap dalam O ( n 2 ). Dalam praktiknya, pengurutan siklik bekerja bahkan beberapa kali lebih lambat daripada pilihan pengurutan biasa, karena Anda harus menjalankan array lebih banyak dan membandingkan lebih sering. Ini adalah harga untuk jumlah penulisan ulang sekecil mungkin.

 #   def cycle(data): #        for cycleStart in range(0, len(data) - 1): value = data[cycleStart] # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      ,   #      if pos == cycleStart: continue #   ,     #        while value == data[pos]: pos += 1 data[pos], value = value, data[pos] #      , #         while pos != cycleStart: # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      #      while value == data[pos]: pos += 1 data[pos], value = value, data[pos] return data


Semacam pancake


Algoritma yang telah menguasai semua tingkat kehidupan - dari bakteri hingga Bill Gates .



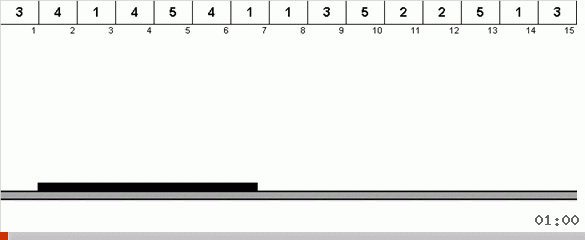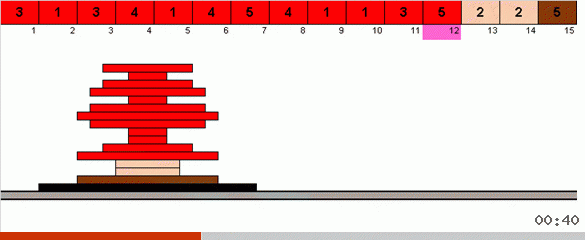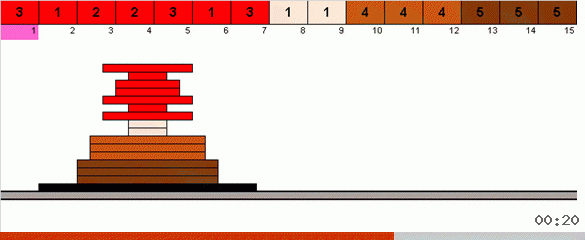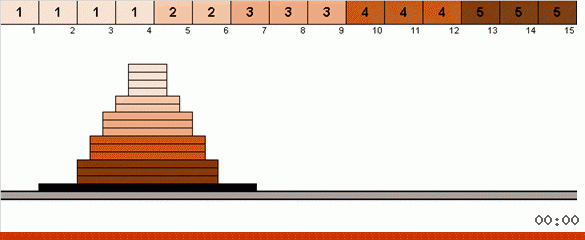
Dalam kasus paling sederhana, kami mencari elemen maksimum di bagian array yang tidak diurutkan. Ketika maksimum ditemukan, kami membuat dua belokan tajam. Pertama, kita memutar rantai elemen sehingga maksimum berada di ujung yang berlawanan. Kemudian kita membalikkan seluruh subarray yang tidak disortir, sebagai hasilnya maksimum jatuh ke tempatnya.

Cordillets seperti itu, secara umum, menyebabkan kompleksitas algoritmik dalam O ( n 3 ). Ciliate yang terlatih ini berjatuhan dalam satu gerakan (oleh karena itu, dalam pelaksanaannya kompleksitasnya adalah O ( n 2 )), dan ketika memprogram, pembalikan bagian array adalah siklus tambahan.

Penyortiran pancake sangat menarik dari sudut pandang matematis (pikiran terbaik berpikir tentang menilai jumlah minimum flips yang cukup untuk menyortir), ada rumusan masalah yang lebih kompleks (dengan apa yang disebut sebagai satu sisi terbakar). Topik pancake sangat menarik, mungkin saya akan menulis monograf yang lebih komprehensif tentang masalah ini.

 #   def pancake(data): if len(data) > 1: for size in range(len(data), 1, -1): #      maxindex = max(range(size), key = data.__getitem__) if maxindex + 1 != size: #    ,    if maxindex != 0: #  , #     data[:maxindex+1] = reversed(data[:maxindex+1]) #    , #      data[:size] = reversed(data[:size]) return data



Penyortiran pemilihan sama efektifnya dengan pencarian elemen minimum / maksimum di bagian array yang tidak disortir. Dalam semua algoritma yang dianalisis hari ini, pencarian dilakukan dalam bentuk pencarian ganda. Dan dalam pencarian ganda, apa pun yang dikatakan, kompleksitas algoritmik akan selalu tidak lebih baik daripada O ( n 2 ). Apakah ini berarti bahwa semua penyortiran berdasarkan pilihan ditakdirkan untuk berarti kompleksitas kuadrat? Tidak sama sekali, jika proses pencarian diatur dengan cara yang secara fundamental berbeda. Misalnya, pertimbangkan dataset sebagai heap dan cari di heap. Namun, topik tumpukan bahkan bukan artikel, tetapi seluruh kisah, kita pasti akan berbicara tentang tumpukan, tetapi lain kali.

Referensi


Seleksi / Siklus , Panekuk / Panekuk

Artikel Seri:



Bingo, siklus, dan panekuk hari ini telah ditambahkan ke aplikasi AlgoLab. Dalam yang terakhir, sehubungan dengan menggambar pancake, pembatasan telah ditempatkan - nilai-nilai elemen dalam array harus dari 1 hingga 5. Anda tentu saja dapat menambahkan lebih banyak, tetapi makro akan secara acak mengambil angka dari kisaran ini.

Source: https://habr.com/ru/post/id422085/

More articles:


All Articles