Richard Hamming: Bab 13. Teori Informasi

Kami berhasil!

"Tujuan kursus ini adalah untuk mempersiapkan Anda untuk masa depan teknis Anda."

Hai, Habr. Ingat artikel yang luar biasa "Kamu dan Pekerjaanmu" (+219, 2588 ditandai, dibaca 429k)?

Jadi Hamming (ya, ya, memeriksa sendiri dan memperbaiki kode Hamming ) memiliki seluruh buku yang ditulis berdasarkan ceramahnya. Kami menerjemahkannya, karena lelaki itu berbicara bisnis.

Buku ini bukan hanya tentang IT, itu adalah buku tentang gaya berpikir orang yang sangat keren. “Ini bukan hanya muatan pemikiran positif; itu menggambarkan kondisi yang meningkatkan peluang melakukan pekerjaan dengan baik. ”

Terima kasih atas terjemahannya ke Andrei Pakhomov.

Teori Informasi dikembangkan oleh C.E. Shannon pada akhir 1940-an. Manajemen Bell Labs bersikeras bahwa ia menyebutnya "Teori Komunikasi," karena ini nama yang jauh lebih akurat. Untuk alasan yang jelas, nama "Teori Informasi" memiliki dampak yang jauh lebih besar pada publik, jadi Shannon memilihnya, dan itulah yang kita ketahui sampai hari ini. Nama itu sendiri menunjukkan bahwa teori ini berkaitan dengan informasi, yang membuatnya penting, karena kita menembus lebih dalam ke era informasi. Dalam bab ini, saya akan menyentuh beberapa kesimpulan dasar dari teori ini, saya tidak akan memberikan bukti yang ketat, tetapi lebih intuitif dari beberapa ketentuan terpisah dari teori ini, sehingga Anda memahami apa sebenarnya "Teori Informasi", di mana Anda dapat menerapkannya dan di mana tidak .

Pertama-tama, apa itu "informasi"? Shannon mengidentifikasi informasi dengan ketidakpastian. Dia memilih logaritma negatif dari probabilitas suatu peristiwa sebagai ukuran kuantitatif dari informasi yang Anda terima ketika suatu peristiwa terjadi dengan probabilitas p. Misalnya, jika saya memberi tahu Anda bahwa cuaca di Los Angeles berkabut, maka p mendekati 1, yang pada umumnya tidak memberi kami banyak informasi. Tetapi jika saya mengatakan bahwa hujan turun di Monterey pada bulan Juni, maka akan ada ketidakpastian dalam pesan ini, dan itu akan berisi lebih banyak informasi. Peristiwa yang andal tidak mengandung informasi apa pun, karena log 1 = 0.

Mari kita bahas ini lebih detail. Shannon percaya bahwa ukuran informasi kuantitatif harus merupakan fungsi berkesinambungan dari probabilitas suatu peristiwa p, dan untuk peristiwa independen harus aditif - jumlah informasi yang diperoleh sebagai hasil dari dua peristiwa independen harus sama dengan jumlah informasi yang diperoleh sebagai hasil dari peristiwa bersama. Misalnya, hasil lemparan dadu dan koin biasanya dianggap sebagai peristiwa independen. Mari kita terjemahkan di atas ke dalam bahasa matematika. Jika I (p) adalah jumlah informasi yang terkandung dalam peristiwa dengan probabilitas p, maka untuk acara gabungan yang terdiri dari dua peristiwa independen x dengan probabilitas p ₁ dan y dengan probabilitas p ₂ kita dapatkan


(x dan y acara independen)

Ini adalah persamaan Cauchy fungsional, berlaku untuk semua p ₁ dan p2. Untuk menyelesaikan persamaan fungsional ini, anggaplah itu

p ₁ = p ₂ = p,

itu memberi



Jika p ₁ = p ² dan p ₂ = p, maka



dll. Memperluas proses ini menggunakan metode standar untuk eksponensial untuk semua bilangan rasional m / n, berikut ini benar



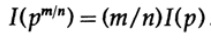
Dari asumsi kontinuitas ukuran informasi, dapat disimpulkan bahwa fungsi logaritmik adalah satu-satunya solusi kontinu terhadap persamaan Cauchy fungsional.

Dalam teori informasi, adalah kebiasaan untuk mengambil basis logaritma 2, sehingga pilihan biner mengandung tepat 1 bit informasi. Karena itu, informasi diukur dengan rumus



Mari kita berhenti dan melihat apa yang terjadi di atas. Pertama-tama, kami tidak memberikan definisi untuk konsep "informasi", kami hanya mendefinisikan formula untuk ukuran kuantitatifnya.

Kedua, ukuran ini tergantung pada ketidakpastian, dan meskipun cukup cocok untuk mesin - misalnya, sistem telepon, radio, televisi, komputer, dll - itu tidak mencerminkan sikap manusia normal terhadap informasi.

Ketiga, ini adalah ukuran relatif, itu tergantung pada kondisi pengetahuan Anda saat ini. Jika Anda melihat aliran "angka acak" dari generator angka acak, Anda menganggap bahwa setiap angka berikutnya tidak pasti, tetapi jika Anda tahu rumus untuk menghitung "angka acak", angka berikutnya akan diketahui dan, karenanya, tidak akan mengandung informasi

Dengan demikian, definisi yang diberikan oleh Shannon untuk informasi dalam banyak kasus cocok untuk mesin, tetapi tampaknya tidak sesuai dengan pemahaman manusia akan kata tersebut. Untuk alasan ini, "Teori Informasi" harus disebut "Teori Komunikasi." Namun, sudah terlambat untuk mengubah definisi (berkat teori yang telah mendapatkan popularitas awalnya, dan yang masih membuat orang berpikir bahwa teori ini berkaitan dengan "informasi"), jadi kita harus tahan dengan mereka, tetapi Anda harus memahami dengan jelas seberapa jauh definisi informasi yang diberikan oleh Shannon jauh dari akal sehatnya. Informasi Shannon berkaitan dengan sesuatu yang sama sekali berbeda, yaitu ketidakpastian.

Inilah yang perlu Anda pikirkan ketika Anda menawarkan terminologi apa pun. Seberapa konsisten definisi yang diusulkan, misalnya, definisi yang diberikan oleh Shannon, dengan ide awal Anda, dan seberapa berbedanya? Hampir tidak ada istilah yang secara akurat akan mencerminkan visi konsep Anda sebelumnya, tetapi pada akhirnya, terminologi yang digunakan yang mencerminkan makna konsep, jadi memformalkan sesuatu melalui definisi yang jelas selalu membuat kebisingan.

Pertimbangkan sistem yang alfabetnya terdiri dari simbol q dengan probabilitas pi. Dalam hal ini, jumlah rata - rata informasi dalam sistem (nilai yang diharapkan) adalah:



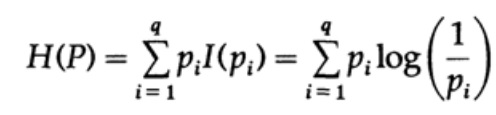
Ini disebut entropi dari sistem distribusi probabilitas {pi}. Kami menggunakan istilah "entropi" karena bentuk matematika yang sama muncul dalam mekanika termodinamika dan statistik. Itulah sebabnya istilah "entropi" menciptakan aura penting di sekelilingnya, yang akhirnya tidak dibenarkan. Bentuk notasi matematika yang sama tidak menyiratkan interpretasi karakter yang sama!

Entropi dari distribusi probabilitas memainkan peran utama dalam teori pengkodean. Ketidaksetaraan Gibbs untuk dua distribusi probabilitas yang berbeda pi dan qi adalah salah satu konsekuensi penting dari teori ini. Jadi kita harus membuktikannya



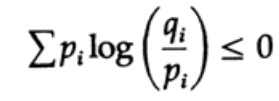
Buktinya didasarkan pada grafik yang jelas, gbr. 13.I, yang menunjukkan itu



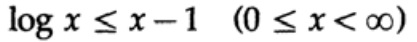
dan persamaan dicapai hanya untuk x = 1. Kami menerapkan ketidaksetaraan untuk setiap jumlah dari jumlah dari sisi kiri:



Jika alfabet sistem komunikasi terdiri dari karakter q, maka dengan mengambil probabilitas transmisi masing-masing karakter, qi = 1 / q dan mengganti q, kita dapatkan dari ketidaksetaraan Gibbs





Gambar 13.I

Ini menunjukkan bahwa jika probabilitas mentransmisikan semua karakter q adalah sama dan sama dengan - 1 / q, maka entropi maksimum adalah ln q, jika tidak, pertidaksamaan berlaku.

Dalam kasus kode yang diterjemahkan secara unik, kami memiliki ketidaksetaraan Kraft



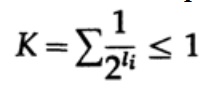
Sekarang jika kita mendefinisikan probabilitas pseudo



dimana tentu saja = 1, yang mengikuti dari ketimpangan Gibbs,



dan menerapkan beberapa aljabar (ingat bahwa K ≤ 1, sehingga kita dapat menghilangkan istilah logaritmik, dan mungkin memperkuat ketidaksetaraan nanti), kita dapatkan



di mana L adalah panjang rata-rata kode.

Dengan demikian, entropi adalah batas minimum untuk setiap kode karakter dengan rata-rata kode sandi L. Ini adalah teorema Shannon untuk saluran tanpa gangguan.

Sekarang kami mempertimbangkan teorema utama tentang keterbatasan sistem komunikasi di mana informasi ditransmisikan dalam bentuk aliran bit independen dan kebisingan hadir. Ini tersirat bahwa probabilitas transmisi yang benar dari satu bit adalah P> 1/2, dan probabilitas bahwa nilai bit akan dibalik selama transmisi (kesalahan terjadi) adalah Q = 1 - P. Untuk kenyamanan, kita mengasumsikan bahwa kesalahan adalah independen dan probabilitas kesalahan adalah sama untuk setiap pengiriman bit - yaitu, ada "white noise" di saluran komunikasi.

Cara kita memiliki aliran panjang n bit yang dikodekan dalam satu pesan adalah ekstensi n-dimensi dari kode satu-bit. Kami akan menentukan nilai n nanti. Pertimbangkan pesan yang terdiri dari n-bit sebagai titik dalam ruang n-dimensi. Karena kita memiliki ruang n-dimensi - dan untuk kesederhanaan kita mengasumsikan bahwa setiap pesan memiliki probabilitas kejadian yang sama - ada pesan M yang mungkin (M juga akan ditentukan kemudian), oleh karena itu, probabilitas setiap pesan yang dikirim sama dengan




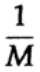
(pengirim)
Bagan 13.II

Selanjutnya, pertimbangkan gagasan bandwidth saluran. Tanpa merinci, kapasitas saluran didefinisikan sebagai jumlah maksimum informasi yang dapat ditransmisikan secara andal melalui saluran komunikasi, dengan mempertimbangkan penggunaan pengkodean yang paling efisien. Tidak ada argumen bahwa lebih banyak informasi dapat dikirim melalui saluran komunikasi daripada kapasitasnya. Ini dapat dibuktikan untuk saluran simetris biner (yang kami gunakan dalam kasus kami). Kapasitas saluran untuk pengiriman bitwise diatur sebagai



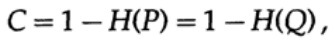
di mana, seperti sebelumnya, P adalah probabilitas tidak ada kesalahan dalam bit yang dikirim. Saat mengirim n bit independen, kapasitas saluran ditentukan sebagai



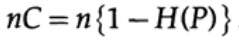
Jika kita dekat dengan bandwidth saluran, maka kita harus mengirim volume informasi yang hampir seperti itu untuk setiap karakter ai, i = 1, ..., M. Mengingat bahwa probabilitas kemunculan setiap karakter ai adalah 1 / M, kita mendapatkan



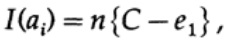
ketika kami mengirim pesan M yang kompatibel, ai, kami miliki



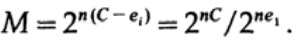
Saat mengirim n bit, kami berharap terjadi kesalahan nQ. Dalam praktiknya, untuk pesan yang terdiri dari n-bit, kami akan memiliki sekitar nQ kesalahan dalam pesan yang diterima. Untuk n besar, variasi relatif (variasi = lebar distribusi,)
distribusi jumlah kesalahan akan semakin sempit dengan meningkatnya n.

Jadi, dari sisi pemancar, saya mengambil pesan ai untuk mengirim dan menggambar bola di sekitarnya dengan jari-jari



yang sedikit lebih besar dengan jumlah yang sama dengan e2 dari jumlah kesalahan yang diharapkan Q, (Gambar 13.II). Jika n cukup besar, maka ada kemungkinan kecil yang sewenang-wenang untuk kemunculan titik pesan bj di sisi penerima, yang melampaui lingkup ini. Kami akan menggambarkan situasinya, seperti yang saya lihat dari sudut pandang pemancar: kami memiliki jari-jari dari pesan yang dikirim ai ke pesan yang diterima bj dengan probabilitas kesalahan sama dengan (atau hampir sama dengan) distribusi normal, mencapai maksimum di nQ. Untuk setiap e2 yang diberikan, ada n begitu besar sehingga probabilitas bahwa titik bj yang dihasilkan, melampaui lingkup saya, akan sekecil yang Anda inginkan.

Sekarang perhatikan situasi yang sama di pihak Anda (Gbr. 13.III). Di sisi penerima ada bola S (r) dari jari-jari yang sama r di sekitar titik yang diterima bj dalam ruang n-dimensi, sehingga jika pesan yang diterima bj berada di dalam bola saya, maka pesan yang saya kirim ada di dalam bola Anda.

Bagaimana kesalahan bisa terjadi? Kesalahan dapat terjadi dalam kasus-kasus yang dijelaskan dalam tabel di bawah ini:



Gambar 13.III



Di sini kita melihat bahwa jika dalam bola yang dibangun di sekitar titik yang diterima ada setidaknya satu titik lagi yang sesuai dengan kemungkinan pesan yang tidak dilode yang dikirim, maka kesalahan terjadi selama transmisi, karena Anda tidak dapat menentukan pesan mana yang dikirim. Pesan yang dikirim tidak mengandung kesalahan hanya jika titik yang sesuai dengan itu di bola, dan tidak ada titik lain yang mungkin dalam kode ini yang berada di bola yang sama.

Kami memiliki persamaan matematika untuk probabilitas kesalahan Re jika ai dikirim



Kita bisa membuang faktor pertama dalam istilah kedua, mengambilnya sebagai 1. Dengan demikian, kita memperoleh ketidaksetaraan



Jelas,



oleh karena itu



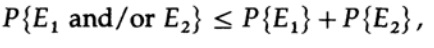
mengajukan kembali ke anggota terakhir di sebelah kanan



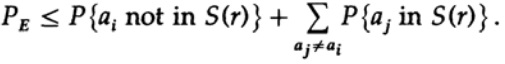
Jika n diambil cukup besar, istilah pertama dapat diambil secara sewenang-wenang kecil, katakanlah, kurang dari jumlah tertentu d. Karena itu kami punya



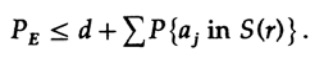
Sekarang mari kita lihat bagaimana Anda dapat membangun kode pengganti yang sederhana untuk menyandikan pesan M yang terdiri dari n bit. Karena tidak tahu bagaimana membangun kode (kode koreksi kesalahan belum ditemukan), Shannon memilih pengkodean acak. Balik koin untuk masing-masing n bit dalam pesan dan ulangi proses untuk pesan M. Yang perlu Anda lakukan adalah lempar koin, jadi itu mungkin



kamus kode memiliki probabilitas yang sama ½nM. Tentu saja, proses acak pembuatan codebook berarti bahwa ada kemungkinan duplikat, serta poin kode, yang akan dekat satu sama lain dan, oleh karena itu, akan menjadi sumber kemungkinan kesalahan. Penting untuk membuktikan bahwa jika ini tidak terjadi dengan probabilitas lebih tinggi dari tingkat kesalahan kecil yang dipilih, maka n yang diberikan cukup besar.
Poin yang menentukan adalah bahwa Shannon rata-rata semua buku kode yang mungkin untuk menemukan kesalahan rata-rata! Kami akan menggunakan Simbol Av [.] Untuk menunjukkan rata-rata dari sekumpulan semua kamus kode acak yang mungkin. Rata-rata atas konstanta d, tentu saja, memberikan konstanta, karena untuk rata-rata setiap istilah bertepatan dengan istilah lain dalam jumlah



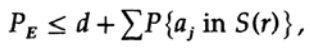
yang dapat ditingkatkan (M - 1 pergi ke M)



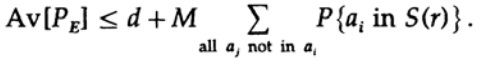
Untuk setiap pesan tertentu, ketika rata-rata semua codebook, pengkodean berjalan melalui semua nilai yang mungkin, sehingga probabilitas rata-rata suatu titik dalam sebuah bola adalah rasio volume bola terhadap total volume ruang. Lingkup bola



di mana s = Q + e2 <1/2 dan ns harus berupa bilangan bulat.

Istilah terakhir di sebelah kanan adalah yang terbesar dalam jumlah ini. Pertama, kami memperkirakan nilainya dengan rumus Stirling untuk faktorial. Kemudian kita melihat koefisien reduksi dari istilah di depannya, perhatikan bahwa koefisien ini meningkat ketika bergerak ke kiri, dan oleh karena itu kita dapat: (1) membatasi nilai jumlah ke jumlah perkembangan geometri dengan koefisien awal ini, (2) memperluas perkembangan geometri dari anggota ns ke jumlah tak terbatas istilah, (3) menghitung jumlah perkembangan geometri tak terbatas (aljabar standar, tidak ada yang signifikan) dan akhirnya mendapatkan nilai batas (untuk n cukup besar):



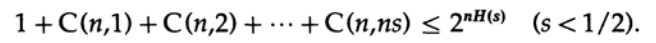
Perhatikan bagaimana entropi H (s) muncul dalam identitas binomial. Perhatikan bahwa ekspansi dalam seri Taylor H (s) = H (Q + e2) memberikan perkiraan yang diperoleh dengan mempertimbangkan hanya turunan pertama dan mengabaikan yang lainnya. Sekarang mari kita kumpulkan ekspresi terakhir:



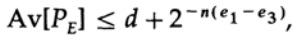
dimana



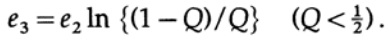
Yang perlu kita lakukan adalah memilih e2 sehingga e3 <e1, dan kemudian suku terakhir akan menjadi kecil, untuk n cukup besar. Oleh karena itu, kesalahan PE rata-rata dapat diperoleh secara kecil dengan kapasitas saluran mendekati sewenang-wenang terhadap C.
Jika rata-rata semua kode memiliki kesalahan yang cukup kecil, maka setidaknya satu kode harus sesuai, oleh karena itu, setidaknya ada satu sistem pengkodean yang sesuai. Ini adalah hasil penting yang diperoleh Shannon - “Teorema Shannon untuk saluran dengan gangguan”, meskipun harus dicatat bahwa ia membuktikannya untuk kasus yang jauh lebih umum daripada untuk saluran simetris biner sederhana yang saya gunakan. Untuk kasus umum, perhitungan matematis jauh lebih rumit, tetapi ide-idenya tidak begitu berbeda, sehingga sangat sering, dengan menggunakan contoh kasus khusus, orang dapat mengungkapkan arti sebenarnya dari teorema tersebut.

Mari kita kritik hasilnya. Kami berulang kali mengulangi: "Untuk n yang cukup besar." Tapi seberapa besar n? Sangat, sangat besar, jika Anda benar-benar ingin secara bersamaan dekat dengan bandwidth saluran dan pastikan transfer data yang benar! Begitu besar sehingga Anda harus menunggu waktu yang sangat lama untuk mengakumulasikan pesan dari banyak bit untuk mengkodekannya nanti. Pada saat yang sama, ukuran kamus kode acak akan sangat besar (setelah semua, kamus seperti itu tidak dapat direpresentasikan dalam bentuk yang lebih pendek dari daftar lengkap semua bit Mn, sementara n dan M sangat besar)!

Kode koreksi kesalahan menghindari menunggu pesan yang sangat panjang, dengan penyandian dan penguraian selanjutnya melalui codebook yang sangat besar, karena mereka menghindari codebook sendiri dan menggunakan perhitungan konvensional sebagai gantinya. Dalam teori sederhana, kode seperti itu, sebagai suatu peraturan, kehilangan kemampuannya untuk mendekati kapasitas saluran dan pada saat yang sama mempertahankan tingkat kesalahan yang cukup rendah, tetapi ketika kode tersebut memperbaiki sejumlah besar kesalahan, mereka menunjukkan hasil yang baik. Dengan kata lain, jika Anda meletakkan beberapa jenis kapasitas saluran untuk koreksi kesalahan, maka Anda harus menggunakan opsi koreksi kesalahan sebagian besar waktu, yaitu, sejumlah besar kesalahan harus diperbaiki dalam setiap pesan yang dikirim, jika tidak, Anda akan kehilangan kapasitas ini untuk apa-apa.

Apalagi teorema yang dibuktikan di atas masih belum berarti! Ini menunjukkan bahwa sistem transmisi yang efisien harus menggunakan skema pengkodean canggih untuk string bit yang sangat panjang. Contohnya adalah satelit yang terbang di luar planet luar; ketika mereka menjauh dari Bumi dan Matahari, mereka dipaksa untuk memperbaiki lebih banyak kesalahan dalam blok data: beberapa satelit menggunakan panel surya, yang menghasilkan sekitar 5 watt, yang lain menggunakan sumber daya atom yang memberikan kekuatan yang sama.Daya lemah dari sumber daya, ukuran kecil pelat pemancar dan ukuran terbatas pelat penerima di Bumi, jarak besar yang harus dilalui sinyal - semua ini membutuhkan penggunaan kode dengan koreksi kesalahan tingkat tinggi untuk membangun sistem komunikasi yang efektif.

Kami kembali ke ruang n-dimensi yang kami gunakan dalam bukti di atas. Membahasnya, kami menunjukkan bahwa hampir seluruh volume bola terkonsentrasi di dekat permukaan luar, - dengan demikian, hampir pasti sinyal yang dikirim akan terletak di permukaan bola yang dibangun di sekitar sinyal yang diterima, bahkan dengan jari-jari bola yang relatif kecil. Oleh karena itu, tidak mengherankan bahwa sinyal yang diterima setelah koreksi dari sejumlah besar kesalahan sewenang-wenang, nQ, ternyata mendekati sewenang-wenang terhadap sinyal tanpa kesalahan. Kapasitas saluran komunikasi, yang kami kaji sebelumnya, adalah kunci untuk memahami fenomena ini. Harap perhatikan bahwa bidang yang dibuat untuk kode koreksi kesalahan Hamming tidak tumpang tindih. Sejumlah besar pengukuran praktis ortogonal dalam pertunjukan ruang n-dimensimengapa kita bisa memasukkan bola M di ruang dengan sedikit tumpang tindih. Jika Anda mengizinkan tumpang tindih kecil, sewenang-wenang kecil, yang hanya dapat menyebabkan sejumlah kecil kesalahan selama decoding, Anda bisa mendapatkan pengaturan padat bola di ruang angkasa. Hamming menjamin tingkat koreksi kesalahan tertentu, Shannon - probabilitas kesalahan yang rendah, tetapi pada saat yang sama mempertahankan bandwidth aktual yang secara sewenang-wenang mendekati kapasitas saluran komunikasi, yang tidak bisa dilakukan kode Hamming.tetapi pada saat yang sama, pelestarian throughput aktual secara sewenang-wenang mendekati kapasitas saluran komunikasi, yang tidak bisa dilakukan kode Hamming.tetapi pada saat yang sama, pelestarian throughput aktual secara sewenang-wenang mendekati kapasitas saluran komunikasi, yang tidak bisa dilakukan kode Hamming.

Teori informasi tidak berbicara tentang bagaimana merancang sistem yang efektif, tetapi itu menunjukkan arah pergerakan menuju sistem komunikasi yang efektif. Ini adalah alat yang berharga untuk membangun sistem komunikasi antar mesin, tetapi, seperti disebutkan sebelumnya, ini tidak ada hubungannya dengan bagaimana orang bertukar informasi satu sama lain. Sejauh mana pewarisan biologis mirip dengan sistem komunikasi teknis sama sekali tidak diketahui, sehingga saat ini tidak jelas bagaimana teori informasi berlaku untuk gen. Kita tidak punya pilihan selain mencoba, dan jika kesuksesan menunjukkan kepada kita sifat seperti mesin dari fenomena ini, maka kegagalan akan mengarah pada aspek signifikan lainnya dari sifat informasi.

Jangan terlalu terganggu. Kita telah melihat bahwa semua definisi awal, pada tingkat yang lebih besar atau lebih kecil, harus mengekspresikan esensi dari keyakinan awal kita, tetapi mereka dicirikan oleh tingkat distorsi tertentu, dan oleh karena itu mereka tidak dapat diterapkan. Secara tradisional diterima bahwa, pada akhirnya, definisi yang kami gunakan sebenarnya mendefinisikan esensi; tetapi, itu hanya memberitahu kita bagaimana memproses sesuatu dan sama sekali tidak masuk akal bagi kita. Pendekatan postulatif, yang sangat diakui di kalangan matematika, menyisakan banyak hal yang diinginkan dalam praktik.

Sekarang kita akan melihat contoh tes IQ, di mana definisinya sama siklus yang Anda inginkan, dan sebagai hasilnya menyesatkan Anda. Sebuah tes dibuat yang seharusnya mengukur kecerdasan. Setelah itu, ditinjau agar sekonsisten mungkin, dan kemudian diterbitkan dan dikalibrasi dengan cara yang sederhana sehingga "kecerdasan" yang diukur terdistribusi secara normal (tentu saja, sepanjang kurva kalibrasi). Semua definisi harus diperiksa silang, tidak hanya ketika mereka pertama kali diusulkan, tetapi jauh kemudian, ketika mereka digunakan dalam kesimpulan yang dibuat. Sejauh mana batasan definisi cocok untuk tugas yang dihadapi? Seberapa sering definisi yang diberikan dalam kondisi yang sama mulai diterapkan dalam kondisi yang sangat berbeda? Ini cukup umum!Dalam humaniora yang pasti akan Anda temui dalam hidup Anda, ini lebih sering terjadi.

Dengan demikian, salah satu tujuan dari presentasi teori informasi ini, selain menunjukkan kegunaannya, adalah untuk memperingatkan Anda tentang bahaya ini, atau untuk menunjukkan bagaimana menggunakannya untuk mendapatkan hasil yang diinginkan. Telah lama diperhatikan bahwa definisi awal menentukan apa yang Anda temukan pada akhirnya, jauh lebih besar daripada yang terlihat. Definisi awal mengharuskan Anda memberi perhatian besar tidak hanya dalam situasi baru apa pun, tetapi juga di area yang sudah lama Anda gunakan. Ini akan memungkinkan Anda untuk memahami sejauh mana hasil yang diperoleh adalah tautologi, dan bukan sesuatu yang berguna.

, . , , , ! , .

...

, — magisterludi2016@yandex.ru

, — «The Dream Machine: » )

, , . ( 10 , 20 )