Sembunyikan tanpa bersembunyi. Sekali lagi tentang steganografi LSB, chi-square dan ... singularitas?

Hari ini, kita akan kembali menaiki sarang tua dan berbicara tentang cara menyembunyikan banyak bit dalam gambar dengan kucing, melihat beberapa alat yang tersedia dan menganalisis serangan paling populer. Dan tampaknya, apa hubungan singularitas dengannya?

Seperti yang mereka katakan, jika Anda ingin mengetahui sesuatu, maka tulislah sebuah artikel tentang itu di Habr! (Perhatian, banyak teks dan gambar)



Steganografi (secara harfiah dari bahasa Yunani "kriptografi") adalah ilmu mentransmisikan data tersembunyi (pesan stego) dalam data terbuka lainnya (stegocontainers) sambil menyembunyikan fakta transfer data. Jangan khawatir, pada kenyataannya, semuanya tidak begitu rumit.

Jadi, di mana dalam gambar Anda bisa menyembunyikan pesan sehingga tidak ada yang memperhatikan?

Dan hanya ada dua tempat: metadata dan gambar itu sendiri. Yang terakhir ini cukup sederhana, cukup ketik "exif" di Google. Jadi mari kita mulai dengan yang kedua.

Sedikit tidak signifikan

Model warna yang paling populer adalah RGB, di mana warna direpresentasikan dalam bentuk tiga komponen: merah, hijau dan biru . Setiap komponen dikodekan dalam versi klasik menggunakan 8 bit, yaitu, dapat mengambil nilai dari 0
ke 255. Di sinilah bit paling signifikan bersembunyi. Adalah penting untuk memahami bahwa satu warna RGB seperti itu menyumbang tiga bit seperti itu.

Untuk menyajikannya dengan lebih jelas, kami akan melakukan beberapa manipulasi kecil.

Seperti yang dijanjikan, ambil gambar kucing dalam format png.



Kami membaginya menjadi tiga saluran dan di setiap saluran kami mengambil bagian yang paling tidak signifikan. Buat tiga gambar baru, di mana setiap piksel mewakili NZB. Nol - piksel putih, unit masing-masing berwarna hitam.

Kami dapat ini.




Tetapi, sebagai suatu peraturan, gambar itu ditemukan dalam "bentuk rakitan." Untuk mewakili NZB dari tiga komponen dalam satu gambar, cukup untuk mengganti komponen dalam piksel di mana NZB bersatu, ganti dengan 255, dan jika tidak ganti dengan 0.

Namun tidak kalah pentingnya

Bayangkan bahwa semua yang kita lihat di gambar terakhir adalah milik kita dan kita memiliki hak untuk melakukan apa pun dengannya. Kemudian kita menganggapnya sebagai aliran bit, dari mana kita bisa membaca dan di mana kita bisa menulis.

Kami mengambil data yang ingin kami selingkan dalam gambar, menyajikannya dalam bentuk bit dan menuliskannya di tempat yang sudah ada.

Untuk mengekstrak data ini, kami membaca NZB sebagai bitstream dan membawanya ke formulir yang diinginkan. Untuk mengetahui berapa banyak bit yang perlu dihitung, sebagai aturan, ukuran pesan dituliskan ke awal. Tetapi ini adalah detail implementasi.

Perlu dicatat bahwa dalam sekitar 50% kasus, bit yang ingin kita tulis dan bit dalam gambar akan bertepatan dan kita tidak perlu mengubah apa pun.

Itu saja, metode berakhir di sini.

Mengapa ini berhasil?

Lihatlah gambar-gambar di bawah ini.

Ini adalah stegocontainer kosong:



Dan ini 95% penuh:



Lihat perbedaannya? Tapi dia benar. Kenapa begitu

Mari kita lihat dua warna: (0, 0, 0) dan (1, 1, 1), yaitu, warna hanya berbeda oleh NZB di setiap komponen.



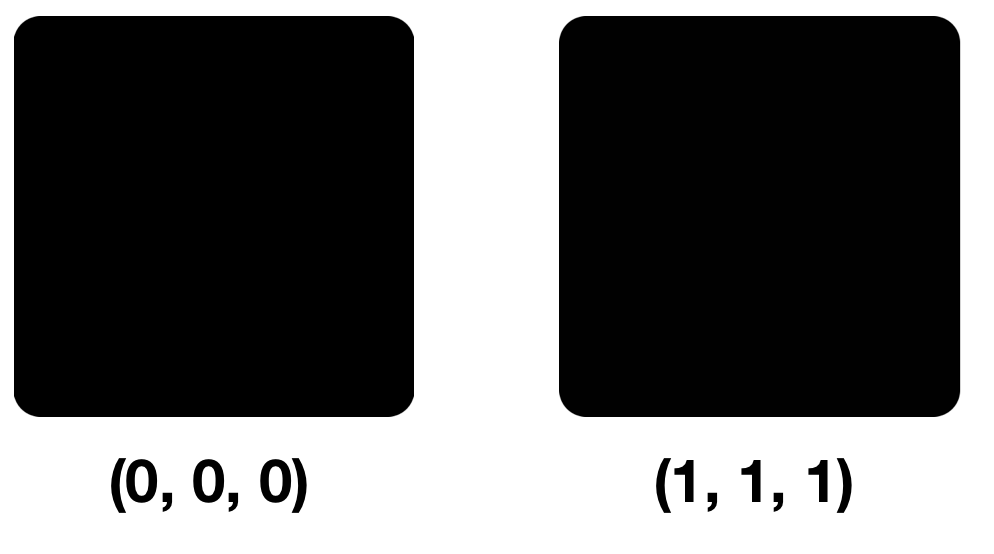
Sedikit perbedaan dalam piksel pada pandangan pertama, kedua dan ketiga tidak akan terlihat. Faktanya adalah bahwa mata kita dapat membedakan sekitar 10 juta warna, dan otak hanya sekitar 150. Model RGB juga mengandung 16.777.216 warna. Anda dapat mencoba membedakan semuanya di sini.

Dari baris perintah

Tidak ada banyak alat baris perintah open source yang tersedia yang mewakili steganografi LSB.

Yang paling populer dapat ditemukan pada tabel di bawah ini.

Dimana kucingnya

Dan yang pertama dalam daftar serangan pada steganografi LSB adalah serangan visual. Kedengarannya aneh, bukan? Bagaimanapun, kucing dengan rahasia tidak mengkhianati dirinya sebagai stegocontainer penuh pada pandangan pertama. Hmmm ... Anda hanya perlu tahu ke mana harus mencari. Mudah ditebak bahwa hanya NZB yang pantas kami perhatikan.

Untuk stegocontainer yang diisi, gambar dengan NZB terlihat seperti ini:



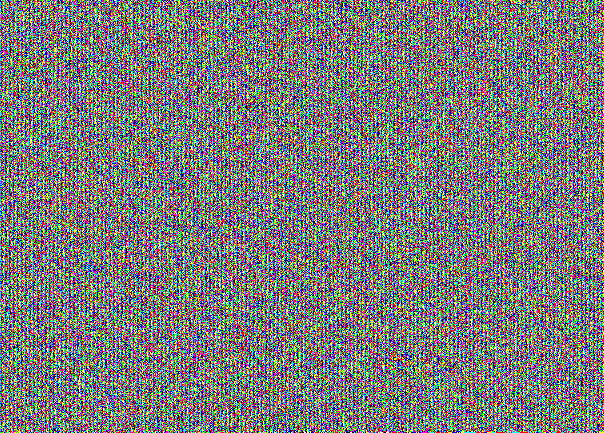
Tidak percaya Di sini Anda memiliki NZB dari ketiga saluran secara terpisah:




Ini adalah "gambar" khusus untuk menyembunyikan pesan di NZB. Pada pandangan pertama, ini seperti suara sederhana. Namun ketika mempertimbangkan strukturnya terlihat. Di sini Anda dapat melihat bahwa stegocontainer sudah penuh. Jika kami menerima pesan sebesar 30% dari kapasitas kucing miskin, kami akan mendapatkan gambar ini:


NZB-nya:



~ 70% kucing tidak berubah.

Di sini perlu dilakukan penyimpangan kecil dan berbicara tentang ukuran. Apa itu kucing 30%? Ukuran kucing adalah 603x433 piksel. 30% dari ukuran ini adalah 78459 piksel. Setiap piksel berisi 3 bit informasi. Total 78459 3 = 235377 bit atau sedikit kurang dari 30 kilobyte cocok dalam 30% dari segel. Dan secara keseluruhan kucing akan muat sekitar 100 kilobyte. Hal-hal seperti itu.

Tetapi kami di sini untuk Anda karena suatu alasan. Lalu, bagaimana cara menipu mata?
Pikiran pertama: memasukkan pesan ke dalam kebisingan. Tapi itu tidak ada di sana. Berikutnya adalah bagian dari stegocontainer yang diisi dan LSB-nya.



Dengan sedikit usaha, kita masih bisa melihat struktur yang akrab. Jangan kehilangan harapan, Tuan-tuan!

Hee hee hee

Banyak hal yang melanggar statistik, Anda tahu.

Mengubah sesuatu dalam gambar, kami mengubah properti statistiknya. Cukup bagi analis untuk menemukan cara untuk memperbaiki perubahan ini.

Chi-square tua yang baik dimulai oleh Andreas Wesfield dan Andreas Pfitzmann dari Universitas Dresden dalam karya mereka “Serangan terhadap Sistem Steganografi”, yang dapat ditemukan di sini.

Selanjutnya, kita akan berbicara tentang serangan dalam bidang warna yang sama, atau dalam konteks RGB, tentang serangan pada satu saluran. Hasil dari setiap serangan dapat dikurangi menjadi rata-rata dan mendapatkan hasil untuk gambar "berkumpul".

Jadi, serangan Chi-square didasarkan pada asumsi bahwa probabilitas kemunculan simultan warna tetangga (berbeda dengan bit paling tidak signifikan) (pasangan nilai) dalam stegocontainer kosong sangat kecil. Benar-benar, Anda bisa mempercayainya. Dengan kata lain, jumlah piksel dari dua warna yang berdekatan secara signifikan berbeda untuk wadah kosong. Yang perlu kita lakukan adalah menghitung jumlah piksel dari setiap warna dan menerapkan beberapa rumus. Sebenarnya, ini adalah tugas sederhana untuk menguji hipotesis menggunakan uji chi-square.

Sedikit matematika?

Biarkan h menjadi array di tempat ke-i yang berisi jumlah piksel warna ke-ke-i pada gambar yang diteliti.

Lalu:

1. Frekuensi warna yang diukur $$$i = 2k$ :
   

   $$

   $$n_k = h [2k], ~ k \ in [0, 127];$$
   
   
2. Frekuensi warna yang diharapkan secara teoritis $$$i = 2k$ :
   

   $$

   $$n_k ^ * = \ frac {h [2k] + h [2k + 1]} {2}, ~ k \ dalam [0,127];$$
   
   

Menerjemahkan ini ke dalam Python akan menghasilkan sesuatu seperti ini:

for k in range(0, len(histogram) // 2): expected.append(((histogram[2 * k] + histogram[2 * k + 1]) / 2)) observed.append(histogram[2 * k]) 

Di mana histogram adalah jumlah piksel warna i dalam gambar, $$$i \ in [0, 255]$

Kriteria chi-square untuk jumlah derajat kebebasan k-1 dihitung sebagai berikut (k adalah jumlah warna yang berbeda, yaitu 256):

$$

$$\ chi_ {k-1} ^ 2 = \ sum_ {i = 1} ^ {k} \ frac {(n_k - n_k ^ *) ^ 2} {n_k ^ *};$$

Dan akhirnya, P adalah probabilitas bahwa distribusi $$$n_i$ dan $$$n_i ^ *$ dalam kondisi ini mereka sama (probabilitas bahwa kita memiliki stegocontainer yang diisi). Itu dihitung dengan mengintegrasikan fungsi kelancaran:

$$

$$P = 1 - \ frac {1} {2 ^ {\ frac {k-1} {2}} \ Gamma (\ frac {k-1} {2})} \ int_0 ^ {\ chi_ {k-1 } ^ 2} e ^ {- \ frac {x} {2}} x ^ {\ frac {k-1} {2} -1} dx;$$

Paling efektif untuk menerapkan chi-square bukan ke seluruh gambar, tetapi hanya ke bagian-bagiannya, misalnya, ke garis. Jika probabilitas yang dihitung untuk garis lebih besar dari 0,5, maka isi garis dalam gambar asli dengan warna merah. Jika kurang, maka hijau. Untuk kucing dengan kepenuhan 30%, gambar akan terlihat sebagai berikut:



Benar sekali, bukan?

Ya, kami mendapat serangan suara yang matematis, Anda tidak bisa menipu matematika! Atau ... ??

Shuffle dance

Idenya cukup sederhana: menulis bit tidak berurutan, tetapi di tempat acak. Untuk melakukan ini, Anda perlu mengambil PRSP, mengkonfigurasinya untuk mengeluarkan aliran acak yang sama dengan sisi yang sama (alias kata sandi). Tanpa mengetahui kata sandi, kami tidak akan dapat mengkonfigurasi PRNG dan menemukan piksel di mana pesan disembunyikan. Kami akan mengujinya pada kucing.

Kitten (32% selesai):



LSB-nya:



Gambarnya terlihat berisik, tetapi tidak mencurigakan bagi seorang analis yang tidak berpengalaman. Apa yang dikatakan Chi-square?


Tampaknya topi hitam menang !? Bagaimanapun caranya ...

Keteraturan-Singularitas

Metode statistik lain adalah Jessica Friedrich, Miroslav Golyan dan Andreas Pfitzman pada tahun 2001. Itu disebut sebagai metode RS. Artikel asli dapat diambil di sini.

Metode ini berisi beberapa langkah persiapan.

Gambar dibagi menjadi kelompok-kelompok n piksel. Misalnya, 4 piksel berturut-turut berturut-turut. Sebagai aturan, grup tersebut mengandung piksel yang berdekatan.
Untuk kucing kami dengan pengisian berurutan di saluran merah, lima kelompok pertama adalah:

• [78, 78, 79, 78]
  
• [78, 78, 78, 78]
  
• [78, 79, 78, 79]
  
• [79, 76, 79, 76]
  
• [76, 76, 76, 77]
  

(Semua pengukuran dalam versi klasik RGB)

Kemudian kita mendefinisikan apa yang disebut fungsi diskriminan atau fungsi kelancaran, yang memetakan setiap kelompok piksel ke bilangan real. Tujuan dari fungsi ini adalah untuk menangkap kelancaran atau "keteraturan" dari kelompok piksel G. Yang lebih berisik kelompok piksel $$$G = (x_1, ..., x_n)$ semakin penting fungsi diskriminan. Paling sering, "variasi" dari sekelompok piksel dipilih, atau, lebih sederhana, jumlah perbedaan piksel tetangga dalam suatu kelompok. Tetapi juga dapat memperhitungkan asumsi statistik tentang gambar.

$$

$$f (x_1, x_2, ..., x_n) = \ sum_ {i = 1} ^ {n-1} | x_ {i + 1} - x_i |$$

Nilai fungsi kelancaran untuk sekelompok piksel dari contoh kami:

• f (78, 78, 79, 78) = 2
• f (78, 78, 78, 78) = 0
• f (78, 79, 78, 79) = 3
• f (79, 76, 79, 76) = 9
• f (76, 76, 76, 77) = 1

Selanjutnya, kelas fungsi membalik dari satu piksel ditentukan.

Mereka harus memiliki beberapa properti.

$$

$$1. ~~~ \ forall x \ di P: ~ F (F (x)) = x, ~~ P = \ {0, ~ 255 \};$$

$$

$$2. ~~~ F_1: 0 \ leftrightarrow 1, ~ 2 \ leftrightarrow 3, ~ ..., 254 \ leftrightarrow 255;$$

$$

$$3 ~~~ \ forall x \ dalam P: ~ F _ {- 1} (x) = F_1 (x + 1) -1;$$

Dimana $$$F$ - fungsi apa pun dari satu kelas, $$$F_1$ Merupakan fungsi membalik langsung, dan $$$F _ {- 1}$ - mundur. Selain itu, fungsi membalik identik biasanya dilambangkan $$$F_0$ yang tidak mengubah piksel.

Fungsi membalik python mungkin terlihat seperti ini:

 def flip(val): if val & 1: return val - 1 return val + 1 def invert_flip(val): if val & 1: return val + 1 return val - 1 def null_flip(val): return val 

Untuk setiap grup piksel, kami menerapkan salah satu fungsi flipping dan berdasarkan nilai fungsi diskriminan sebelum dan sesudah flipping, kami menentukan jenis grup pixel: normal ( R egular), tunggal / tidak biasa ( S ingular), dan tidak dapat digunakan. Karena jenis yang terakhir tidak digunakan lebih lanjut, metode ini dinamai setelah huruf pertama dari jenis kunci. Itulah seluruh rahasia nama, singularitas tidak ada hubungannya dengan itu :)



Kami mungkin ingin menerapkan pembalikan yang berbeda ke piksel yang berbeda, untuk ini kami mendefinisikan mask M dengan nilai n -1, 0 atau 1.

$$

$$F_M (G) = (F_ {M (1)} (x_1), F_ {M (2)} (x_2), ..., F_ {M (n)} (x_n))$$

Biarkan topeng untuk contoh kita menjadi klasik - [1, 0, 0, 1]. Secara eksperimental ditemukan bahwa topeng simetris itu tidak mengandung $$$F _ {- 1}$ . Pilihan yang juga berhasil adalah: [0, 1, 0, 1], [0, 1, 1, 0], [1, 0, 1, 0]. Kami menerapkan pembalikan untuk grup dari contoh, menghitung nilai kelancaran dan menentukan jenis grup piksel:

• $$$F_m$ (78, 78, 79, 78) = [79, 78, 79, 79];
  f (79, 78, 79, 79) = 2 = 2 = f (78, 78, 79, 78)
  Grup Tidak Dapat Digunakan
  
  
• $$$F_m$ (78, 78, 78, 78) = [79, 78, 78, 79];
  f (79, 78, 78, 79) = 2> 0 = f (78, 78, 78, 78)
  Grup biasa
  
  
• $$$F_m$ (78, 79, 78, 79) = [79, 79, 78, 78];
  f (79, 79, 78, 78) = 1 <3 = f (78, 79, 78, 79) Grup tunggal
  
  
• $$$F_m$ (79, 76, 79, 76) = [78, 76, 79, 77];
  f (78, 76, 79, 77) = 7 <9 = f (79, 76, 79, 76) Grup tunggal
  
  
• $$$F_m$ (76, 76, 76, 77) = [77, 76, 76, 76];
  f (77, 76, 76, 76) = 1 = 1 = f (76, 76, 76, 77)
  Grup Tidak Dapat Digunakan
  
  

Kami menunjukkan jumlah grup reguler untuk topeng M sebagai $$$R_M$ (dalam persentase semua kelompok), dan $$$S_M$ untuk kelompok tunggal.

Lalu $$$R_M + S_M \ leq 1$ dan $$$R _ {- M} + S _ {- M} \ leq 1$ , untuk topeng negatif (semua komponen masker dikalikan dengan -1), karena $$$R_M + S_M + U_M = 1$ sementara $$$U_M$ mungkin kosong. Demikian pula untuk topeng negatif.

Hipotesis statistik utama adalah bahwa dalam gambar tipikal nilai yang diharapkan $$$R_M$ sama dengan $$$R _ {- M}$ , dan hal yang sama berlaku untuk $$$S_M$ dan $$$S _ {- M}$ . Ini dibuktikan dengan data eksperimental dan beberapa tarian dengan rebana di sekitar properti terakhir dari fungsi flipping.

$$

$$R_M \ cong S_M ~~~~ R _ {- M} \ cong S _ {- M}$$

Mari kita periksa contoh kecil kita? Mengingat ukuran sampel yang kecil, kami mungkin tidak mengkonfirmasi hipotesis ini. Mari kita lihat apa yang terjadi dengan topeng terbalik: [-1, 0, 0, -1].

• F_M (78, 78, 79, 78) = [77, 78, 79, 77];
  f (77, 78, 79, 77) = 4> 2 = f (77, 78, 79, 77)
  Grup biasa
  
  
• F_M (78, 78, 78, 78) = [77, 78, 78, 77];
  f (77, 78, 78, 77) = 2> 0 = f (78, 78, 78, 78)
  Grup biasa
  
  
• F_M (78, 79, 78, 79) = [77, 79, 78, 80];
  f (77, 79, 78, 80) = 5> 3 = f (78, 79, 78, 79)
  Grup biasa
  
  
• F_M (79, 76, 79, 76) = [80, 76, 79, 75];
  f (80, 76, 79, 75) = 11> 9 = f (79, 76, 79, 76)
  Grup biasa
  
  
• F_M (76, 76, 76, 77) = [75, 76, 76, 78];
  f (75, 76, 76, 78) = 3> 1 = f (76, 76, 76, 77)
  Grup biasa
  
  

Ya, semuanya jelas.

Namun perbedaannya antara $$$R_M$ dan $$$S_M$ cenderung nol karena panjang m dari pesan yang disematkan meningkat dan kami mendapatkannya $$$R_M \ cong S_M$ .

Lucu bahwa pengacakan pesawat LSB memiliki efek sebaliknya $$$R _ {- M}$ dan $$$S _ {- M}$ . Perbedaannya bertambah dengan panjang m dari pesan yang disematkan. Penjelasan tentang fenomena ini dapat ditemukan di artikel asli.

Inilah jadwalnya $$$R_M$ , $$$S_M$ , $$$R _ {- M}$ dan $$$S _ {- M}$ tergantung pada jumlah piksel dengan LSB terbalik, itu disebut diagram RS. Sumbu x adalah persentase piksel dengan LSB terbalik, sumbu y adalah jumlah relatif kelompok reguler dan tunggal dengan topeng M dan -M, $$$M = [0 ~ 1 ~ 1 ~ 0]$ .



Inti dari metode steganalisis RS adalah untuk mengevaluasi empat kurva diagram RS dan menghitung persimpangan mereka menggunakan ekstrapolasi. Misalkan kita memiliki stegocontainer dengan pesan panjang yang tidak diketahui p (sebagai persentase piksel) yang tertanam dalam bit yang lebih rendah dari piksel yang dipilih secara acak (mis. Menggunakan RandomLSB). Pengukuran awal kami tentang jumlah grup R dan S sesuai dengan poin $$$R_M (p / 2)$ , $$$S_M (p / 2)$ , $$$R _ {- M} (p / 2)$ dan $$$S _ {- M} (p / 2)$ . Kami mengambil poin dari tepat setengah panjang pesan, karena pesan adalah aliran bit acak dan rata-rata, seperti disebutkan sebelumnya, hanya setengah dari piksel yang akan diubah dengan menyematkan pesan.

Jika kami membalikkan LSB dari semua piksel dalam gambar dan menghitung jumlah grup R dan S, kami mendapatkan empat poin $$$R_M (1-p / 2)$ , $$$S_M (1-p / 2)$ , $$$R _ {- M} (1-p / 2)$ dan $$$S _ {- M} (1-p / 2)$ . Karena dua poin ini bergantung pada pengacakan spesifik LSB, kita harus mengulangi proses ini berkali-kali dan mengevaluasi $$$R_M (1/2)$ dan $$$S_M (1/2)$ dari sampel statistik.

Kami dapat menarik garis melalui titik secara kondisional $$$R _ {- M} (p / 2)$ , $$$R _ {- M} (1-p / 2)$ dan $$$S _ {- M} (p / 2)$ , $$$S _ {- M} (1-p / 2)$ .

Poin $$$R_M (p / 2)$ , $$$R_M (1/2)$ , $$$R_M (1-p / 2)$ dan $$$S_M (p / 2)$ , $$$S_M (1/2)$ , $$$S_M (1-p / 2)$ mendefinisikan dua parabola. Setiap parabola dan garis yang bersilangan berpotongan di sebelah kiri. Mean aritmatik dari koordinat x dari kedua persimpangan memungkinkan kita untuk memperkirakan panjang pesan yang tidak diketahui p.

Untuk menghindari estimasi statistik panjang titik tengah RM (1/2) dan SM (1/2), beberapa pertimbangan lain dapat diambil:

1. Titik persimpangan kurva $$$R_M$ dan $$$R _ {- M}$ memiliki koordinat x yang sama dengan titik persimpangan untuk kurva $$$S_M$ dan $$$S _ {- M}$ . Ini pada dasarnya adalah versi yang lebih ketat dari hipotesis statistik kami. (lihat di atas)
2. Kurva RM dan SM berpotongan pada m = 50%, atau $$$R_M (1/2) = S_M (1/2)$ .

Dua asumsi ini memberikan formula sederhana untuk panjang pesan rahasia h. Setelah menskalakan sumbu x sehingga p / 2 menjadi 0 dan 1 - p / 2 menjadi 1, koordinat x dari titik persimpangan adalah akar dari persamaan kuadrat berikut



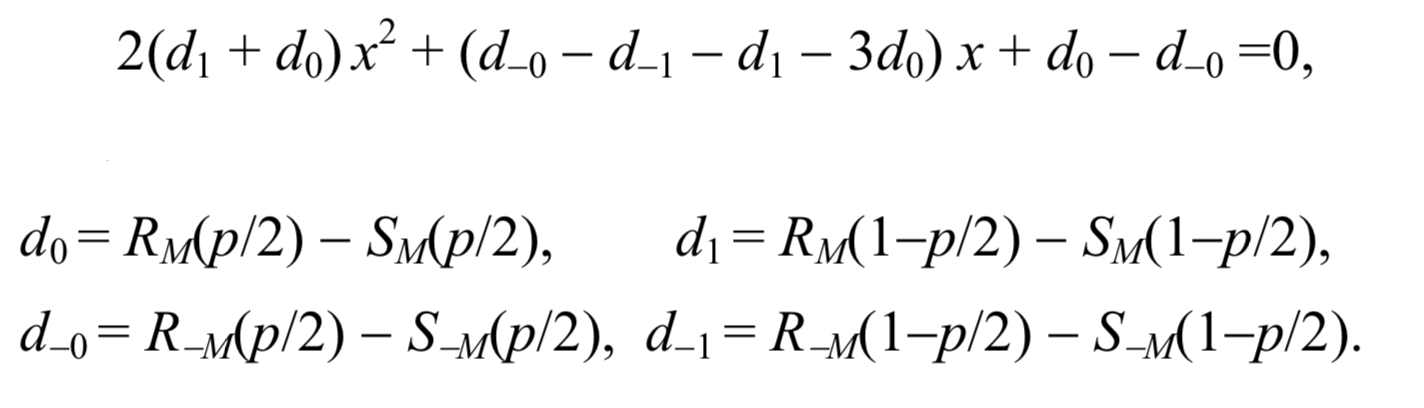
Maka panjang pesan dapat dihitung dengan rumus:

$$

$$p = \ frac {x} {x- \ frac {1} {2}}$$

Di sini kucing kita memasuki lokasi. (Bukankah sudah waktunya untuk memberinya nama?)

Jadi kita punya:

• Grup RM biasa (p / 2): 23121 pcs.
• Grup SM tunggal (p / 2): 14124 pcs.
• Grup reguler dengan masker terbalik RM (hal / 2): 37191 pcs.
• Grup tunggal dengan topeng terbalik SM (p / 2): 8440 pcs.
• Grup reguler dengan LSB RM terbalik (1-p / 2): 20298 pcs.
• Grup tunggal dengan LSB SM terbalik (1-p / 2): 16206 pcs.
• Grup reguler dengan LSB terbalik dan masker terbalik RM (1-p / 2): 40603 pcs.
• Kelompok tunggal dengan LSB terbalik dan dengan topeng terbalik SM (1-p / 2): 6947 pcs.

(Jika Anda memiliki banyak waktu luang, maka Anda dapat menghitungnya sendiri, tetapi untuk sekarang saya sarankan Anda percaya perhitungan saya)

Dalam agenda, kami telah meninggalkan satu matematika kosong. Masih ingat bagaimana cara memecahkan persamaan kuadrat?

$$

$$d_0 = 8997$$

$$

$$d _ {- 0} = $ 2875$$

$$

$$d_1 = 4092$$

$$

$$d _ {- 1} = 33656$$

Mengganti semua d dalam rumus di atas, kita memperoleh persamaan kuadrat, yang kita pecahkan seperti yang diajarkan di sekolah.

$$

$$26178x ^ 2-35988x - 19754 = 0$$

$$

$$D = (-35988) ^ 2 - 426178 * (- 19754) = $ 336361699$$

$$

$$x_1 = 1.7951 ~~~~~~~~ x_2 = -0,4204$$

Ambil akar modulus yang lebih kecil , mis. $$$x_2$ . Maka perkiraan perkiraan untuk pesan yang dimasukkan ke dalam kucing adalah sebagai berikut:

$$

$$p = \ frac {-0,4204} {- 0,4204 - 0,5} = 0,4567$$

Ya, metode ini memiliki satu plus besar dan satu minus besar. Keuntungannya adalah bahwa metode ini bekerja dengan steganografi LSB biasa dan steganografi RandomLSB. Chi-square tidak bisa membanggakan kesempatan seperti itu. Metode ini mengenali kucing yang tampak acak kami secara akurat dan memperkirakan panjang pesan di 0,3256, yang sangat, sangat akurat.

Yang minus terletak pada kesalahan besar (sangat besar) dari metode ini, yang tumbuh seiring dengan pesan panjang dengan embedding berurutan . Misalnya, untuk kucing dengan hunian 30%, penerapan metode ini memberikan perkiraan rata-rata untuk tiga saluran 0,4633 atau 46% dari total kapasitas, dengan hunian lebih dari 95% - 0,8597. Tetapi untuk kucing kosong sebanyak 0,0054. Dan ini adalah tren umum yang tidak tergantung pada implementasi. Hasil paling akurat dengan metode LSB biasa memberikan panjang pesan bawaan 10% + - 5%.

Plus atau minus

Agar tidak ketahuan, harus ada yang tak terduga dan menggunakan ± 1 coding. Alih-alih mengubah bit paling signifikan dalam byte warna, kami akan menambah atau mengurangi seluruh byte dengan satu. Hanya ada dua pengecualian:

• kita tidak bisa mengurangi nol, karena itu kita akan meningkatkannya,
  
• kami juga tidak dapat menambah 255, jadi kami akan selalu menurunkan nilai ini.
  

Untuk semua nilai byte lainnya, kami sepenuhnya memilih secara acak salah satu peningkatan dengan satu atau penurunan. Di atas manipulasi ini, LSB akan berubah seperti sebelumnya. Untuk keandalan yang lebih besar, lebih baik mengambil byte acak untuk merekam pesan.

Ini kucing teman kita:



Secara lahiriah, pendahuluan tidak terlihat persis karena alasan yang sama mengapa perbedaan antara (0, 0, 0) dan (1, 1, 1) tidak terlihat.



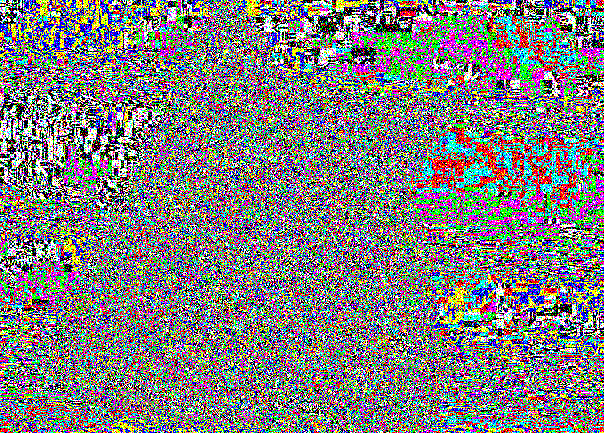
Irisan LSB tetap berisik karena perekaman di tempat acak.



Chi-square masih buta, dan metode RS memberikan perkiraan kasar 0,0036 .

Untuk tidak senang, baca artikel ini di sini.

Yang paling penuh perhatian mungkin bertanya bagaimana kita bisa mendapatkan pesan jika seluruh byte diubah secara acak, dan kami tidak memiliki kata sandi untuk mengatur PRNG (lebih baik menggunakan benih yang berbeda alias keadaan generator alias kata sandi untuk bekerja dengan RandomLSB dan ± 1 pengkodean). Jawabannya sesederhana mungkin. Kami menerima pesan dengan cara yang sama kami lakukan tanpa ± 1 encoding. Kita bahkan mungkin tidak tahu tentang penggunaannya. Saya ulangi, kami menggunakan trik ini hanya untuk memotong alat deteksi otomatis . Saat menyematkan / mengambil pesan, kami hanya bekerja dengan LSB dan tidak lebih. Namun, ketika mendeteksi, kita perlu memperhitungkan konteks implementasi, yaitu, semua byte gambar, untuk membangun estimasi statistik. Inilah tepatnya keseluruhan keberhasilan ± 1 coding.

Alih-alih sebuah kesimpulan

Upaya lain yang sangat baik untuk menggunakan statistik terhadap steganografi LSB dibuat dalam metode yang disebut Pasangan Sampel. Anda dapat menemukannya di sini. Kehadirannya di sini akan membuat artikel itu terlalu akademis, jadi saya meninggalkannya tertarik untuk membaca ekstrakurikuler. Tetapi mengantisipasi pertanyaan audiens, saya akan segera menjawab: tidak, dia tidak menangkap ± 1 coding.

Dan tentu saja pembelajaran mesin. Metode modern berdasarkan ML memberikan hasil yang sangat baik. Anda dapat membacanya di sini dan di sini .

Berdasarkan artikel ini, alat kecil ditulis (untuk saat ini). Ini dapat menghasilkan data, melakukan serangan visual secara terpisah pada saluran, menghitung RS-, penilaian SPA dan memvisualisasikan hasil Chi-square. Dan dia tidak akan berhenti di situ.

Sebagai rangkuman, saya ingin memberikan beberapa tips:

• Sematkan pesan dalam byte acak.
• Kurangi jumlah informasi yang disematkan sebanyak mungkin (ingat Paman Hamming).
• Gunakan ± 1 coding.
• Pilih gambar dengan LSB berisik.
• UPD Remdalp : Gunakan gambar yang tidak muncul di mana pun.
• Baiklah!

Saya akan senang melihat saran, tambahan, koreksi, dan umpan balik Anda lainnya!

PS Saya ingin mengucapkan terima kasih khusus kepada PavelMSTU untuk konsultasi dan tendangan motivasi.