Pengantar sederhana untuk ALU untuk jaringan saraf: penjelasan, makna fisik dan implementasi

Baru-baru ini, para peneliti di Google DeepMind, termasuk seorang ilmuwan kecerdasan buatan terkenal, penulis buku " Understanding Deep Learning, " Andrew Trask, menerbitkan sebuah artikel yang mengesankan yang menggambarkan model jaringan saraf untuk mengekstrapolasi nilai-nilai fungsi numerik sederhana dan kompleks dengan tingkat akurasi yang tinggi.

Dalam posting ini saya akan menjelaskan arsitektur NALU ( perangkat logika aritmatika neural, NALU), komponennya dan perbedaan signifikan dari jaringan saraf tradisional. Tujuan utama dari artikel ini adalah untuk secara sederhana dan intuitif menjelaskan NALU (baik implementasi maupun ide) untuk para ilmuwan, programmer dan siswa yang baru mengenal jaringan saraf dan pembelajaran yang mendalam.

Catatan dari penulis : Saya juga sangat merekomendasikan membaca artikel asli untuk studi topik yang lebih rinci.

Kapan jaringan saraf salah?

Gambar diambil dari artikel ini.

Secara teori, jaringan saraf harus memperkirakan fungsi dengan baik. Mereka hampir selalu dapat mengidentifikasi korespondensi yang signifikan antara input data (faktor atau fitur) dan output (label atau target). Itulah sebabnya jaringan saraf digunakan di banyak bidang, dari pengenalan objek dan klasifikasinya hingga menerjemahkan ucapan ke dalam teks dan mengimplementasikan algoritma permainan yang dapat mengalahkan juara dunia. Banyak model yang berbeda telah dibuat: jaringan saraf convolutional dan berulang, autocoder, dll. Keberhasilan dalam menciptakan model baru jaringan saraf dan pembelajaran yang mendalam adalah topik besar itu sendiri.

Namun, menurut penulis artikel itu, jaringan saraf tidak selalu mengatasi tugas-tugas yang tampak jelas bagi manusia dan bahkan lebah ! Misalnya, ini adalah akun lisan atau operasi dengan angka, serta kemampuan untuk mengidentifikasi ketergantungan dari hubungan. Artikel tersebut menunjukkan bahwa model standar jaringan saraf bahkan tidak dapat mengatasi pemetaan identik (fungsi yang menerjemahkan argumen ke dalam dirinya sendiri, $$$f (x) = x$) Apakah hubungan numerik yang paling jelas. Gambar di bawah ini menunjukkan MSE dari berbagai model jaringan saraf ketika mempelajari nilai-nilai fungsi ini.


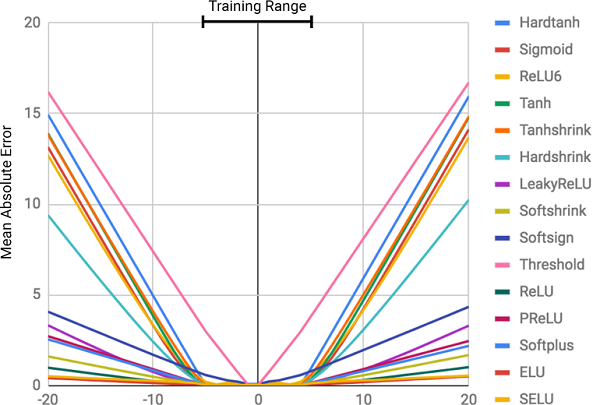Gambar ini menunjukkan kesalahan kuadrat rata-rata untuk jaringan saraf standar menggunakan arsitektur yang sama dan fungsi aktivasi (non-linear) yang berbeda di lapisan dalam

Mengapa jaringan saraf salah?

Seperti dapat dilihat dari gambar, alasan utama untuk kesalahan adalah nonlinier dari fungsi aktivasi pada lapisan dalam jaringan saraf. Pendekatan ini bekerja sangat baik untuk menentukan hubungan non-linear antara input data dan respons, tetapi sangat salah untuk melampaui data yang dipelajari jaringan. Dengan demikian, jaringan saraf melakukan pekerjaan yang sangat baik untuk mengingat ketergantungan numerik dari data pelatihan, tetapi mereka tidak dapat memperkirakannya.

Ini seperti menjejalkan jawaban atau topik sebelum ujian tanpa memahami materi pelajaran. Mudah untuk lulus ujian jika pertanyaannya mirip dengan pekerjaan rumah, tetapi jika pemahaman tentang subjek yang sedang diuji, dan bukan kemampuan untuk mengingat, kita akan gagal.


Ini bukan program kursus!

Tingkat kesalahan terkait langsung dengan tingkat nonlinier dari fungsi aktivasi yang dipilih. Diagram sebelumnya jelas menunjukkan bahwa fungsi nonlinear dengan kendala keras, seperti sigmoid atau hiperbolik tangen ( Tanh ), dapat mengatasi tugas generalisasi dependensi yang jauh lebih buruk daripada fungsi yang dibatasi lunak, seperti transformasi linear terpotong ( ELU , PReLU ).

Solusi: Neural Battery (NAC)

Baterai neural ( NAC ) adalah jantung dari model NALU . Ini adalah bagian yang sederhana namun efektif dari jaringan saraf yang mengatasi penambahan dan pengurangan , yang diperlukan untuk perhitungan efisien hubungan linier.

NAC adalah lapisan linier khusus dari jaringan syaraf tiruan, dengan beratnya syarat sederhana diberlakukan: mereka hanya dapat mengambil 3 nilai - 1, 0 atau -1 . Pembatasan tersebut tidak memungkinkan baterai untuk mengubah kisaran data input, dan tetap konstan pada semua lapisan jaringan, terlepas dari jumlah dan koneksinya. Dengan demikian, output adalah kombinasi linear dari nilai - nilai vektor input, yang dapat dengan mudah menjadi operasi penjumlahan dan pengurangan.

Pikiran keras : untuk pemahaman yang lebih baik dari pernyataan ini, mari kita lihat contoh membangun lapisan jaringan saraf yang melakukan operasi aritmatika linier pada data input.


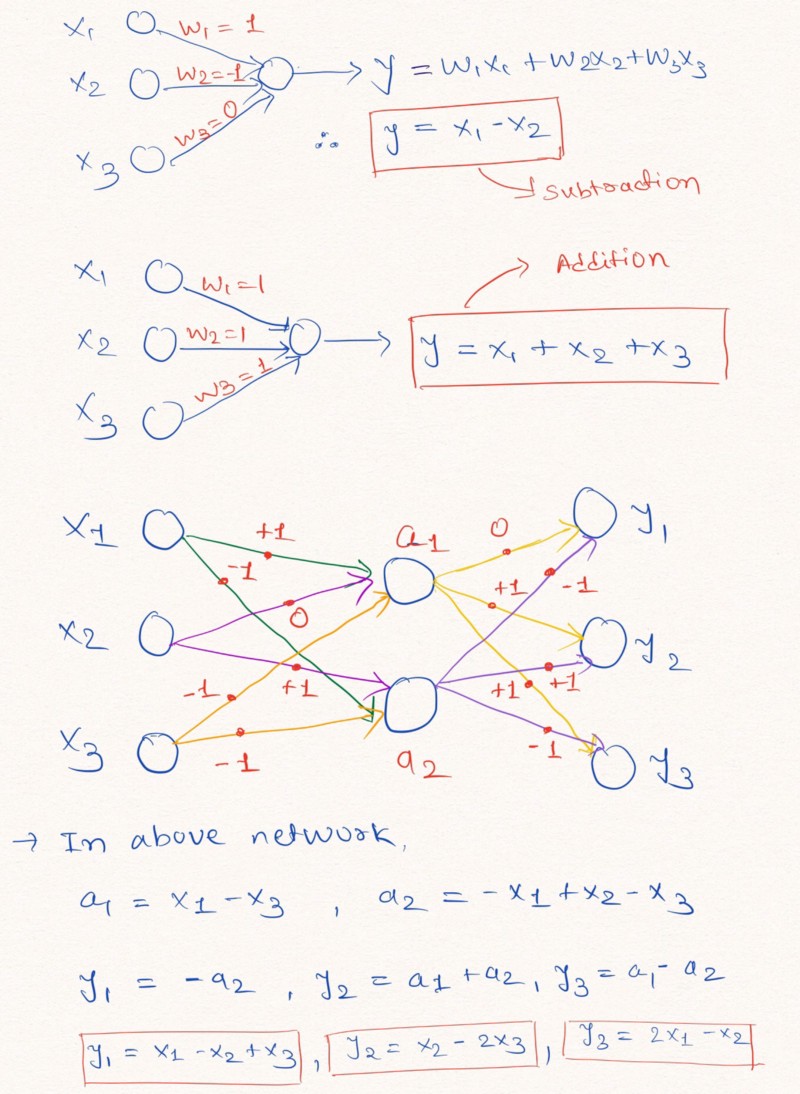Gambar tersebut menggambarkan bagaimana lapisan jaringan saraf tanpa menambahkan konstanta dan dengan kemungkinan nilai bobot -1, 0 atau 1, dapat melakukan ekstrapolasi linier

Seperti yang ditunjukkan di atas dalam gambar lapisan, jaringan saraf dapat belajar untuk meramalkan nilai-nilai fungsi aritmatika sederhana seperti penambahan dan pengurangan ( $$$y = x_1 + x_2$dan $$$y = x_1 - x_2$), menggunakan batasan bobot dengan kemungkinan nilai 1, 0 dan -1.

Catatan: lapisan NAC dalam kasus ini tidak mengandung istilah bebas (konstan) dan tidak menerapkan transformasi non-linear ke data.

Karena jaringan saraf standar tidak dapat mengatasi solusi masalah di bawah pembatasan yang sama, penulis artikel menawarkan formula yang sangat berguna untuk menghitung parameter tersebut melalui parameter klasik (tidak terbatas) $$$\ hat {W}$dan $$$\ hat {M}$. Data berat, seperti semua parameter jaringan saraf, dapat diinisialisasi dan dipilih secara acak dalam proses pelatihan jaringan. Formula untuk menghitung vektor $$$W$melalui $$$\ hat {W}$dan $$$\ hat {M}$terlihat seperti ini:

$$

$$W = tanh (\ hat {W}) \ odot \ sigma (\ hat {M})$$

Rumusnya menggunakan produk matriks elemenwise

Menggunakan rumus ini memastikan bahwa kisaran nilai W terbatas pada interval [-1, 1], yang lebih dekat ke himpunan -1, 0, 1. Selain itu, fungsi dari persamaan ini dapat dibedakan berdasarkan parameter bobot. Dengan demikian, akan lebih mudah bagi lapisan NAC kita untuk mempelajari nilai-nilai $$$W$menggunakan gradient descent dan back propagation of error . Berikut ini adalah diagram arsitektur lapisan NAC .


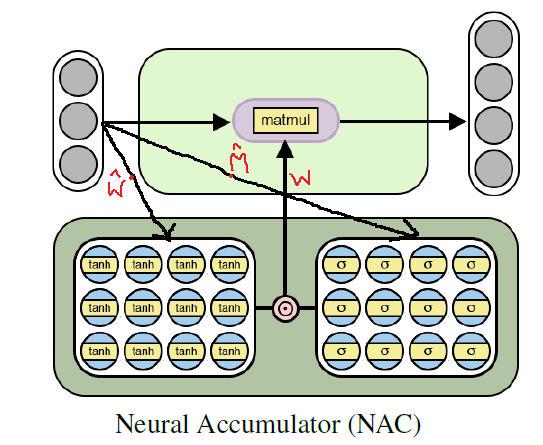Arsitektur baterai saraf untuk pelatihan fungsi aritmatika dasar (linier)

Implementasi Python NAC Menggunakan Tensorflow

Seperti yang telah kita pahami, NAC adalah jaringan saraf yang cukup sederhana (lapisan jaringan) dengan fitur kecil. Berikut ini adalah implementasi dari lapisan NAC tunggal di Python menggunakan pustaka Tensoflow dan NumPy.


Dalam kode di atas $$$\ hat {W}$dan $$$\ hat {M}$diinisialisasi menggunakan distribusi seragam, tetapi Anda dapat menggunakan metode yang direkomendasikan untuk menghasilkan perkiraan awal untuk parameter ini. Anda dapat melihat versi lengkap dari kode di repositori GitHub saya (tautannya digandakan di akhir posting).

Pindah: Dari Penambahan dan Pengurangan ke NAC untuk Ekspresi Aritmatika Kompleks

Meskipun model jaringan saraf sederhana yang dijelaskan di atas berupaya dengan operasi sederhana seperti penjumlahan dan pengurangan, kita harus dapat belajar dari banyak arti fungsi yang lebih kompleks, seperti multiplikasi, pembagian, dan eksponensial.

Di bawah ini adalah arsitektur NAC yang dimodifikasi, yang diadaptasi untuk pemilihan operasi aritmatika yang lebih kompleks melalui logaritma dan mengambil eksponen di dalam model. Perhatikan perbedaan antara implementasi KPA ini dan yang sudah dibahas di atas.


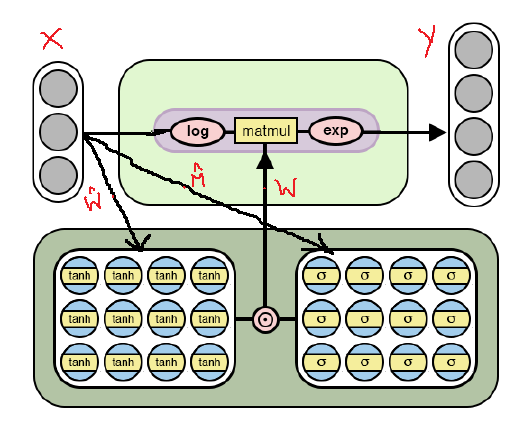Arsitektur NAC untuk operasi aritmatika yang lebih kompleks

Seperti dapat dilihat dari gambar, kita logaritma input data sebelum dikalikan dengan matriks bobot, dan kemudian menghitung eksponen hasilnya. Rumus untuk perhitungan adalah sebagai berikut:

$$

$$Y = exp (W \ bullet (log (| x | + \ epsilon)))$$

Rumus output untuk versi kedua NAC . $$$\ epsilon$di sini adalah jumlah yang sangat kecil untuk mencegah situasi seperti log (0) selama pelatihan

Dengan demikian, untuk kedua model NAC , prinsip operasi termasuk perhitungan bobot matriks dengan batasan $$$W$melalui $$$\ hat {W}$dan $$$\ hat {M}$tidak berubah. Satu-satunya perbedaan adalah penggunaan operasi logaritmik pada input dan output dalam kasus kedua.

Versi NAC kedua dalam Python menggunakan Tensorflow

Kode, seperti arsitekturnya, tidak akan berubah, kecuali untuk perbaikan yang ditunjukkan dalam penghitungan tensor nilai output.



Saya mengingatkan Anda lagi bahwa versi lengkap dari kode dapat ditemukan di repositori GitHub saya (tautannya diduplikasi di akhir posting).

Menyatukan semuanya: unit logika aritmatika saraf (NALU)

Seperti yang sudah banyak ditebak, kita dapat belajar dari hampir semua operasi aritmatika, menggabungkan dua model yang dibahas di atas. Ini adalah gagasan utama NALU , yang mencakup kombinasi bobot NAC dasar dan kompleks, yang dikendalikan melalui sinyal pelatihan. Dengan demikian, NAC adalah blok bangunan untuk membangun NALU , dan jika Anda memahami desainnya, membangun NALU akan mudah. Jika Anda masih memiliki pertanyaan, coba baca penjelasan untuk kedua model NAC lagi. Di bawah ini adalah diagram dengan arsitektur NALU .


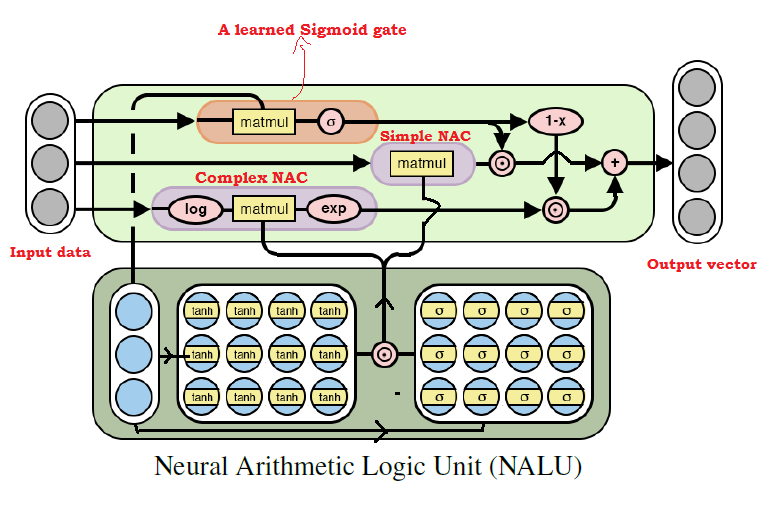Diagram arsitektur NALU dengan penjelasan

Seperti dapat dilihat dari gambar di atas, kedua unit NAC (blok ungu) di dalam NALU diinterpolasi (digabungkan) melalui sinyal pelatihan sigmoid (blok oranye). Ini memungkinkan Anda untuk (de) mengaktifkan output dari salah satu dari mereka, tergantung pada fungsi aritmatika, nilai-nilai yang kami coba temukan.

Seperti disebutkan di atas, unit elementer NAC adalah fungsi akumulasi, yang memungkinkan NALU untuk melakukan operasi linier elementer (penambahan dan pengurangan), sedangkan unit NAC yang kompleks bertanggung jawab untuk perkalian, pembagian, dan eksponensial. Output dalam NALU dapat direpresentasikan sebagai formula:


Dari rumus NALU di atas, kita dapat menyimpulkan bahwa dengan $$$g = 0$jaringan saraf hanya akan memilih nilai untuk operasi aritmatika kompleks, tetapi tidak untuk yang elementer; dan sebaliknya - dalam kasus $$$g = 1$. Dengan demikian, secara umum, NALU dapat mempelajari operasi aritmatika, yang terdiri dari menambah, mengurangi, mengalikan, membagi dan meningkatkan daya, dan berhasil mengekstrapolasi hasil di luar rentang nilai-nilai data sumber.

Implementasi Python NALU menggunakan Tensorflow

Dalam implementasi NALU, kita akan menggunakan NAC dasar dan kompleks, yang telah kita definisikan.


Sekali lagi, saya perhatikan bahwa dalam kode di atas, saya kembali menginisialisasi matriks parameter $$$G$menggunakan distribusi yang seragam, tetapi Anda dapat menggunakan cara apa pun yang disarankan untuk menghasilkan perkiraan awal.

---

Ringkasan

Bagi saya pribadi, ide NALU adalah terobosan besar di bidang AI, terutama di jaringan saraf, dan itu terlihat menjanjikan. Pendekatan ini dapat membuka pintu ke area aplikasi di mana jaringan saraf standar tidak dapat mengatasinya.

Para penulis artikel tersebut berbicara tentang berbagai percobaan menggunakan NALU : dari memilih nilai-nilai fungsi aritmatika dasar hingga menghitung jumlah digit tulisan tangan dalam serangkaian gambar MNIST , yang memungkinkan jaringan saraf untuk memeriksa program-program komputer!

Hasilnya membuat kesan yang menakjubkan dan membuktikan bahwa NALU mengatasi hampir semua tugas yang berkaitan dengan representasi numerik, lebih baik daripada model standar jaringan saraf. Saya mendorong pembaca untuk membiasakan diri dengan hasil percobaan untuk lebih memahami bagaimana dan di mana model NALU dapat bermanfaat.

Namun, harus diingat bahwa NAC maupun NALU bukanlah solusi ideal untuk tugas apa pun. Sebaliknya, mereka mewakili ide umum tentang cara membuat model untuk kelas operasi aritmatika tertentu.

---

Di bawah ini adalah tautan ke repositori GitHub saya, yang berisi implementasi penuh kode dari artikel.
github.com/faizan2786/nalu_implementation

Anda dapat secara independen memeriksa operasi model saya pada berbagai fungsi dengan memilih hyperparameters untuk jaringan saraf. Silakan ajukan pertanyaan dan bagikan pemikiran Anda dalam komentar di bawah pos ini, dan saya akan melakukan yang terbaik untuk menjawab Anda.

PS (dari penulis): ini adalah posting pertama saya yang pernah ditulis, jadi jika Anda memiliki tips, saran dan rekomendasi untuk masa depan (baik teknis dan umum), silakan menulis kepada saya.

PPS (dari penerjemah): jika Anda memiliki komentar pada terjemahan atau teks, silakan tulis pesan pribadi kepada saya. Saya terutama tertarik pada kata-kata untuk sinyal gerbang terpelajar - saya tidak yakin bisa menerjemahkan istilah ini dengan akurat.