Konsep komputasi malas hampir tidak layak dibicarakan secara rinci. Gagasan untuk melakukan hal yang sama lebih jarang, terutama jika itu panjang dan sulit, sama tuanya dengan dunia. Karena langsung to the point.
Menurut penulis teks ini, seorang pemberi penjelasan yang normal harus:
- Simpan penghitungan antara panggilan program.
- Lacak perubahan di pohon perhitungan.
- Memiliki sintaksis yang cukup transparan.

Konsep
Dalam rangka:
- Simpan penghitungan antara panggilan program:
Memang, jika kita memanggil skrip yang sama beberapa puluh ratusan kali sehari, mengapa kita harus menghitung ulang hal yang sama setiap kali skrip dipanggil, jika memungkinkan untuk menyimpan objek hasil dalam file. Lebih baik menarik objek dari disk, tetapi ... kita harus yakin akan relevansinya. Tiba-tiba skrip ditulis ulang dan objek yang disimpan kedaluwarsa. Berdasarkan hal ini, kita tidak bisa hanya memuat objek berdasarkan keberadaan file. Poin kedua mengikuti dari ini. - Lacak perubahan di pohon perhitungan:
Kebutuhan untuk memperbarui objek harus dihitung berdasarkan data tentang argumen fungsi yang menghasilkannya. Jadi kami akan memastikan bahwa objek yang dimuat valid. Memang, untuk fungsi murni, nilai kembali hanya bergantung pada argumen. Ini berarti bahwa sementara kami menyimpan hasil dari fungsi murni dan memantau perubahan argumen, kami bisa tenang tentang relevansi cache. Pada saat yang sama, jika objek yang dihitung bergantung pada objek cache lainnya (malas), yang pada gilirannya tergantung pada objek lain, Anda perlu mengetahui perubahan-perubahan pada objek-objek ini dengan tepat, memperbarui tepat waktu node rantai yang tidak lagi relevan. Di sisi lain, alangkah baiknya untuk memperhitungkan bahwa kita tidak selalu perlu memuat data dari seluruh rantai perhitungan. Seringkali, hanya memuat objek hasil akhir sudah cukup. - Memiliki sintaksis yang cukup transparan:
Poin ini jelas. Jika untuk menulis ulang skrip ke perhitungan malas perlu mengubah seluruh kode, ini adalah solusi begitu-begitu. Perubahan harus dilakukan seminimal mungkin.
Garis pemikiran ini mengarah pada solusi teknis, ditata dalam python oleh perpustakaan evalcache (tautan di akhir artikel).
Solusi sintaksis dan mekanisme kerja
Contoh sederhanaimport evalcache import hashlib import shelve lazy = evalcache.Lazy(cache = shelve.open(".cache"), algo = hashlib.sha256) @lazy def summ(a,b,c): return a + b + c @lazy def sqr(a): return a * a a = 1 b = sqr(2) c = lazy(3) lazyresult = summ(a, b, c) result = lazyresult.unlazy() print(lazyresult)
Bagaimana cara kerjanya?
Hal pertama yang menarik perhatian Anda di sini adalah penciptaan dekorator malas. Solusi sintaksis semacam itu cukup standar untuk Python python. Dekorator malas melewati objek cache di mana lenificator akan menyimpan hasil perhitungan. Persyaratan antarmuka seperti dict ditumpangkan pada jenis cache. Dengan kata lain, kita dapat men-cache semua yang mengimplementasikan antarmuka yang sama dengan tipe dict. Untuk menunjukkan dalam contoh di atas, kami menggunakan kamus dari perpustakaan rak.
Dekorator juga mengirim protokol hash, yang akan ia gunakan untuk membuat kunci hash objek dan beberapa opsi tambahan (izin tulis, izin baca, hasil debug), yang dapat ditemukan dalam dokumentasi atau kode.
Dekorator dapat diterapkan untuk fungsi dan objek dari jenis lain. Pada saat ini, objek malas dibangun atas dasar mereka dengan kunci hash yang dihitung berdasarkan representasi (atau menggunakan fungsi hash yang didefinisikan secara khusus untuk jenis fungsi ini).
Fitur utama dari perpustakaan adalah bahwa objek malas dapat menghasilkan objek malas lainnya, dan hash orang tua (atau orang tua) akan dicampur menjadi kunci hash keturunan. Untuk objek yang malas, diizinkan untuk menggunakan operasi mengambil atribut, menggunakan panggilan ( __call__ ) objek, dan menggunakan operator.
Saat melewati skrip, pada kenyataannya, tidak ada perhitungan yang dilakukan. Untuk b, kuadratnya tidak dihitung, dan untuk lazyresult, jumlah argumen tidak dipertimbangkan. Sebagai gantinya, pohon operasi dibangun dan kunci hash objek malas dihitung.
Perhitungan nyata (jika hasilnya sebelumnya tidak dimasukkan ke dalam cache) akan dilakukan hanya di baris: result = lazyresult.unlazy()
Jika objek sebelumnya dihitung, itu akan diambil dari file.
Anda dapat memvisualisasikan pohon build:
Membangun visualisasi pohon evalcache.print_tree(lazyresult) ... generic: <function summ at 0x7f1cfc0d5048> args: 1 generic: <function sqr at 0x7f1cf9af29d8> args: 2 ------- 3 -------
Karena hash objek dibangun berdasarkan data pada argumen yang menghasilkan objek-objek ini, ketika argumen berubah, hash objek berubah dan disertai hash seluruh rantai tergantung padanya. Ini memungkinkan Anda untuk tetap memperbarui data cache dengan membuat pembaruan tepat waktu.
Objek malas berbaris di pohon. Jika kita melakukan operasi yang tidak benar pada salah satu objek, persis seperti banyak objek akan dimuat dan dihitung seperlunya untuk mendapatkan hasil yang valid. Idealnya, objek yang diperlukan hanya akan memuat. Dalam hal ini, algoritma tidak akan menarik objek membentuk ke dalam memori.
Beraksi
Di atas adalah contoh sederhana yang menunjukkan sintaks tetapi tidak menunjukkan kekuatan komputasi dari pendekatan.
Berikut adalah contoh yang sedikit lebih dekat dengan kehidupan nyata (digunakan oleh sympy).
Contoh menggunakan sympy dan numpy Operasi untuk menyederhanakan ekspresi simbolik sangat mahal dan benar-benar meminta lenifikasi. Pembangunan lebih lanjut dari array besar bahkan lebih lama, tetapi berkat lenifikasi, hasilnya akan ditarik dari cache. Harap perhatikan bahwa jika ada koefisien yang diubah di bagian atas skrip tempat ekspresi sympy dihasilkan, hasilnya akan dihitung ulang karena kunci hash objek malas akan berubah (berkat pernyataan __repr__ keren).
Cukup sering, situasi terjadi ketika seorang peneliti melakukan eksperimen komputasi pada objek yang dihasilkan lama. Ini dapat menggunakan beberapa skrip untuk memisahkan pembuatan dan penggunaan objek, yang dapat menyebabkan masalah dengan pembaruan data yang tidak tepat waktu. Pendekatan yang diusulkan dapat memfasilitasi kasus ini.
Tentang apa semua ini?
evalcache adalah bagian dari proyek zencad. Ini adalah skrip skrip kecil, menginspirasi dan mengeksploitasi ide yang sama dengan openscad. Tidak seperti openscad yang berorientasi mesh, zencad yang berjalan pada inti opencascade menggunakan representasi brep dari objek, dan skrip ditulis dengan python.
Operasi geometris sering dilakukan untuk waktu yang lama. Kerugian dari sistem skrip cad adalah bahwa setiap kali Anda menjalankan skrip, produk tersebut benar-benar diceritakan kembali. Selain itu, dengan pertumbuhan dan komplikasi model, biaya overhead tidak tumbuh secara linear. Ini mengarah pada fakta bahwa Anda dapat bekerja dengan nyaman hanya dengan model yang sangat kecil.
Tugas evalcache adalah merapikan masalah ini. Di zencad, semua operasi dinyatakan malas.
Contoh:
Contoh membangun model
Script ini menghasilkan model berikut:
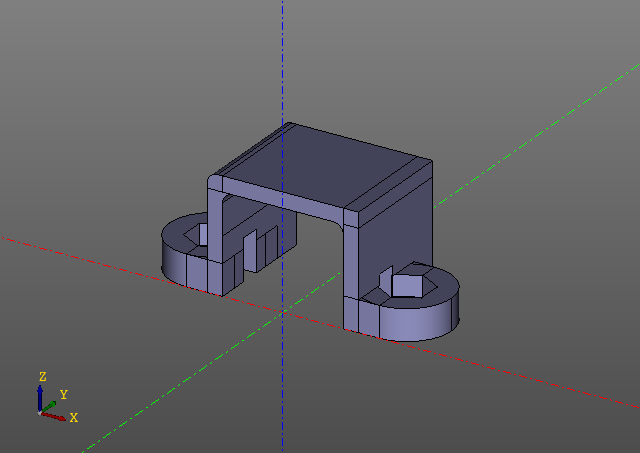
Perhatikan bahwa tidak ada panggilan evalcache di skrip. Kuncinya adalah bahwa lenifikasi tertanam di perpustakaan zencad itu sendiri dan bahkan tidak terlihat pada pandangan pertama, meskipun semua pekerjaan di sini bekerja dengan benda-benda malas, dan perhitungan langsung dilakukan hanya dalam fungsi 'tampilan'. Tentu saja, jika beberapa parameter model diubah, model akan dihitung ulang dari tempat di mana kunci hash pertama berubah.
Model Komputasi BesarIni adalah contoh lain. Kali ini kami akan membatasi diri pada gambar:
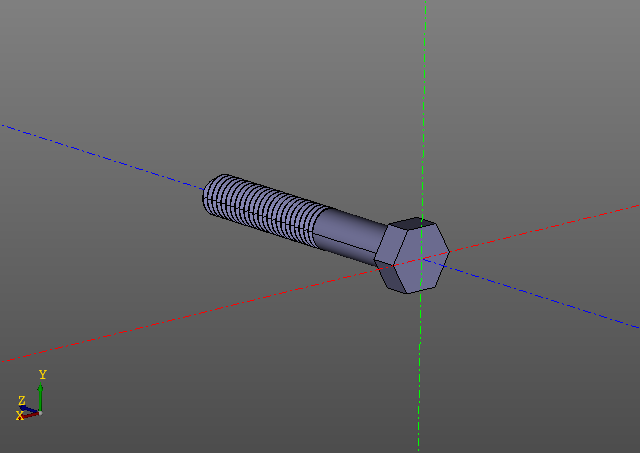
Perhitungan permukaan berulir bukanlah tugas yang mudah. Di komputer saya, baut seperti itu dibangun di atas urutan sepuluh detik ... Mengedit model dengan ulir jauh lebih menyenangkan menggunakan caching.
Dan sekarang ini adalah keajaiban:

Melintasi permukaan berulir adalah tugas komputasi yang kompleks. Nilai praktis, bagaimanapun, tidak lain adalah memeriksa matematika. Perhitungannya membutuhkan satu setengah menit. Tujuan yang layak untuk lenifikasi.
Masalahnya
Cache mungkin tidak berfungsi sebagaimana dimaksud.
Kesalahan cache dapat dibagi menjadi false positif dan false negatif .
Kesalahan Negatif Palsu
Kesalahan negatif palsu adalah situasi di mana hasil perhitungan ada dalam cache, tetapi sistem tidak menemukannya.
Ini terjadi jika algoritma kunci hash yang digunakan oleh evalcache untuk beberapa alasan menghasilkan kunci yang berbeda untuk perhitungan ulang. Jika fungsi hash tidak diganti untuk objek dari tipe yang di-cache, evalcache menggunakan __repr__ objek untuk membangun kunci.
Kesalahan terjadi, misalnya, jika kelas yang disewa tidak menimpa object.__repr__ standar object.__repr__ , yang berubah dari awal hingga awal. Atau, jika __repr__ ditimpa, entah bagaimana tergantung pada tidak signifikannya perhitungan data yang berubah (seperti alamat objek atau cap waktu).
Buruk:
class A: def __init__(self): self.i = 3 A_lazy = lazy(A) A_lazy().unlazy()
Baik:
class A: def __init__(self): self.i = 3 def __repr__(self): return "A({})".format(self.i) A_lazy = lazy(A) A_lazy().unlazy()
Kesalahan negatif palsu mengarah pada fakta bahwa lenifikasi tidak berfungsi. Objek akan dihitung ulang pada setiap eksekusi skrip baru.
Kesalahan positif palsu
Ini adalah jenis kesalahan yang lebih kejam, karena mengarah ke kesalahan dalam objek akhir perhitungan:
Itu bisa terjadi karena dua alasan.
- Luar biasa:
Tabrakan kunci hash terjadi di cache. Untuk algoritma sha256 memiliki ruang 115792089237316195423570985008687907853269984665640564039457584007913129639936 kemungkinan kunci, kemungkinan tabrakan diabaikan. - Mungkin:
Representasi objek (atau fungsi hash yang ditimpa) tidak sepenuhnya menggambarkannya, atau bertepatan dengan representasi objek tipe lain.
class A: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) class B: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) A_lazy = lazy(A) B_lazy = lazy(B) a = A_lazy().unlazy() b = B_lazy().unlazy()
Kedua masalah terkait dengan objek __repr__ tidak kompatibel. Jika karena alasan tertentu tidak mungkin untuk menimpa tipe objek __repr__ , perpustakaan memungkinkan Anda untuk mengatur fungsi hash khusus untuk tipe pengguna.
Tentang analog
Ada banyak pustaka lenifikasi yang pada dasarnya menganggap cukup untuk menjalankan perhitungan tidak lebih dari sekali per panggilan skrip.
Ada banyak pustaka caching disk yang, atas permintaan Anda, akan menyimpan objek dengan kunci yang diperlukan untuk Anda.
Tapi saya masih tidak bisa menemukan perpustakaan yang memungkinkan hasil caching di pohon eksekusi. Jika ada, tolong, tidak aman.
Referensi:
Proyek Github
Proyek Pypi