Melewati kompromi - Anda bisa menikah!

Pendahuluan

Metode elemen hingga (FEM atau FEM, mereka miliki di luar negeri) dengan kuat masuk ke dalam praktik perhitungan rekayasa dalam desain sistem yang kompleks. Sebagian besar, ini berkaitan dengan perhitungan kekuatan mekanika. Penerapan metode ini, diimplementasikan oleh perangkat lunak yang sesuai, secara signifikan mempersingkat siklus pengembangan perangkat akhir, menghilangkan massa pemeriksaan eksperimental yang diperlukan ketika menggunakan perhitungan klasik berdasarkan metode sopromat dan mekanika struktural. Sampai saat ini, banyak perangkat lunak aplikasi telah dikembangkan yang mengimplementasikan FEM. Di garis depan adalah ANSYS yang kuat, di sisi itu dan pada jarak kehormatan - sistem CAD dengan modul FEM bawaan (SolidWorks, Siemens NX, Creo Parametric, Compass 3D).

CalculiX kuat, tetapi sulit dan tidak bisa dipahami. Akankah kita memperbaikinya?



Secara alami, FEM telah merambah ke bidang pendidikan - untuk menggunakannya dalam tugas nyata, pelatihan spesialis yang relevan diperlukan. Di ibukota, di universitas teknis besar, situasi di daerah ini lebih atau kurang normal, dan di wilayah kami ANSYS yang sama digunakan, misalnya, di Departemen Teori Elastisitas Universitas Federal Selatan. Tetapi di pinggiran, di universitas yang sedikit terspesialisasi dan tidak kaya, situasinya menyedihkan. Dan itu sederhana - ANSYS menghabiskan sekitar 2 juta rubel untuk satu tempat kerja, dan diperlukan lebih dari satu tempat. Sayangnya, tidak semua universitas mampu membayar 30-40 juta untuk menyelenggarakan kelas komputer untuk mengajarkan penggunaan FEM.

Salah satu alternatifnya adalah penggunaan perangkat lunak gratis dalam proses pendidikan. Untungnya, perangkat lunak tersebut tersedia. Namun, praktis tidak ada bahan berbahasa Rusia dalam penggunaannya. Memperbaiki situasi ini, saya akan mencurahkan artikel ini untuk pengenalan CalculiX - paket perangkat lunak bebas dan terbuka yang dirancang untuk menyelesaikan masalah tiga dimensi linear dan nonlinear dari mekanika dari benda padat yang dapat dideformasi dan mekanika fluida dan gas menggunakan metode elemen hingga.

1. Apa itu Kalkuli dan di mana mendapatkannya. Instalasi Windows

Paket CalculiX adalah seperangkat utilitas konsol, termasuk preprosesor untuk menyiapkan data sumber, pemecah FEM, dan prosesor pos untuk memproses hasilnya. CalculiX digunakan baik secara mandiri maupun sebagai bagian dari produk lain, di antaranya FreeCAD mendapatkan momentum. Pertanyaan lain adalah bahwa CalculiX masih sedikit dikenal di negara kita, yang secara langsung dinyatakan oleh satu - satunya artikel tentang hal ini di sumber ini .

Saya secara khusus akan menyatakan materi berikut berkenaan dengan bekerja di Windows, sebagai yang paling umum dan digunakan termasuk lembaga pendidikan. Selain itu, penggunaan banyak program gratis di dalamnya adalah rasa sakit terbuka.

Jika Anda mengambil paket Windows dari situs web CalculiX resmi, itu menjadi sepenuhnya tidak jelas apa yang harus dilakukan selanjutnya. Dalam hubungannya dengan dokumentasi berbahasa Inggris, itu mengakhiri produk ini bagi banyak orang, dan kemudian diterjemahkan menjadi komentar beracun tentang ketidakmungkinan penggunaannya. Dan sebagian ini benar - ambang untuk masuk sangat tinggi. Tapi tetap kita akan coba.

Ada sejumlah build yang relatif tidak ramah untuk pemula dari keajaiban ini untuk Windows, di antaranya bConverged CalculiX untuk Windows . Kami mengunduh kit distribusi dari sini , membongkar, dan menginstalnya menggunakan metode standar "lanjut, lanjut ...". Instalasi, oleh karena itu, bukan merupakan misteri khusus dan cukup dapat diakses oleh pengguna yang tidak berpengalaman. Sebagai lingkungan kerja utama, paket ini menggunakan editor teks SciTE, yang mengintegrasikan panggilan ke komponen CalculiX, serta kemungkinan input perintah interaktif dan terlihat seperti ini (dapat diklik).

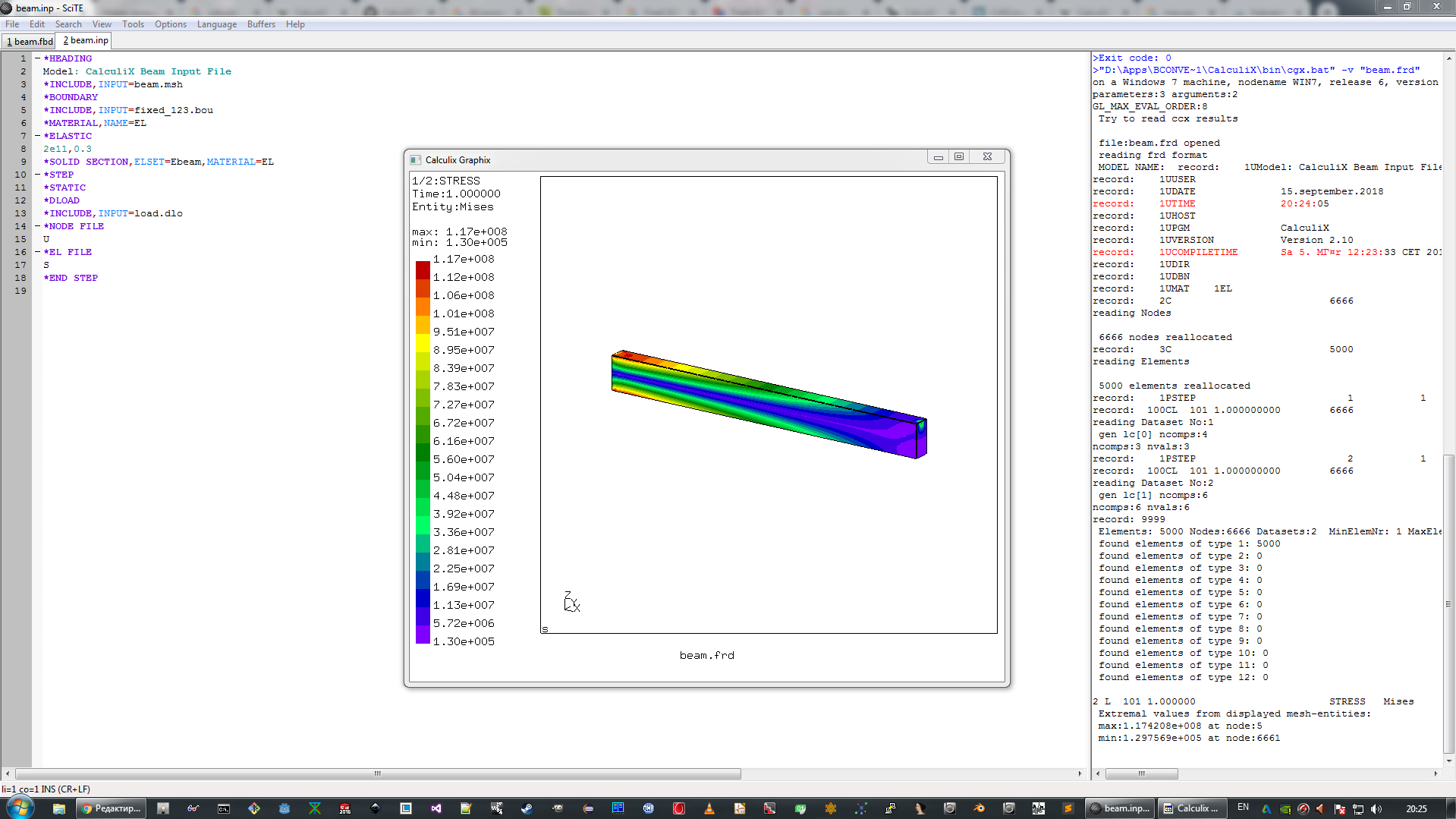
2. Masalah balok lentur dan solusi analitisnya menggunakan metode sopromat

Ambil masalah siswa yang sederhana - pembengkokan balok baja, salah satu ujungnya terjepit, dan gaya vertikal F diterapkan ke yang lain.



Parameter masalah adalah sebagai berikut: F = 10 kN; l = 1 m adalah panjang balok; h = 0,1 m dan b = 0,05 m adalah dimensi dari penampang. Untuk kesederhanaan, kami tidak akan memperhitungkan berat balok sendiri, karena berat balok 39 kg, secara signifikan lebih kecil dari beban yang diterapkan. Kami menemukan tegangan normal maksimum di bagian balok dan juga menghitung lendutan balok karena deformasi lentur.

Siswa mana pun yang tidak melewatkan kompromi akan dengan mudah menyelesaikan masalah seperti itu. Agar tidak mempermalukan para bangsawan, saya akan membungkus semua detail keputusan dalam spoiler


Bagi mereka yang terlalu malas untuk melihat di bawah spoiler, saya akan segera memberikan jawaban untuk masalah ini: tegangan normal maksimum di bagian balok $$$\ sigma_x = 119$ MPa, dan defleksi maksimum adalah 3,97 mm. Angka-angka ini diberikan untuk perbandingan selanjutnya dengan apa prosedur untuk memecahkan masalah ini di CalculiX akan memberi kita.

3. Persiapan geometri dan grid komputasi

Pertama-tama, Anda perlu memasukkan data geometris tentang bagian yang dimaksud ke CalculiX. Ya, dimungkinkan untuk mengekspor geometri dari CAD, seperti yang dilakukan dalam ANSYS yang sama, tetapi kami akan melalui penyiksaan dan memasukkan geometri secara manual. Buka editor SciTE dari kit bConverged dan ketikkan teks berikut ini

pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0

Simpan file dengan nama beam.fbd dan tekan F10 untuk memulai preprocessing. Kita akan melihat sesuatu seperti berikut ini



Perintah pnt membuat titik dalam ruang dengan koordinat yang diberikan dan sintaksnya adalah sebagai berikut

pnt [ ] [x] [y] [z]

Sekarang hubungkan titik-titik ini dengan garis, menambahkan teks berikut ke file

line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25

yang diterima setelah menekan F10 gambar berikut



Tim

line [ ] [ 1] [ 2] [ ]

menciptakan garis yang menghubungkan titik-titik yang ditunjukkan di dalamnya, menambahkan titik tengah yang membagi garis menjadi sejumlah segmen tertentu (dalam kasus kami, 25 untuk setiap baris). Ini akan berguna nanti untuk pembuatan grid. Sekarang lakukan tipuan dengan telinga kita

seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10

Tim pertama

seta [ ] [ 1] ... [ N]

menggabungkan beberapa objek menjadi satu set dengan nama yang diberikan. Bahkan, ini adalah analog dari pengelompokan objek. Perintah selanjutnya

swep [ ] [ ] [ ] [, ] []

Memindahkan set objek yang dipilih untuk membentuk set baru. Objek bergerak disalin. Dalam hal ini, pergerakan titik membentuk garis, pergerakan garis - permukaan, pergerakan permukaan - volume kontinu. Dalam kasus kami, kami menggeser set garis garis sepanjang sumbu Z sebesar 0,1 meter, sedangkan garis yang dihasilkan dibagi menjadi 10 segmen. Kami menekan F10 ... eh, dan apa itu?



Ghm, layar kosong ... Mudah diperbaiki, cukup tambahkan baris di akhir skrip

plot pa all
plus la all

Perintah-perintah ini memberitahu Anda untuk menggambar semua titik (pa) dan menambahkan semua garis (la) ke layar, setelah itu kami mendapatkan hasil ini



Sekarang mari kita membuat permukaan berdasarkan set garis yang kita buat

seta surfaces s A001 A002 A003 A004

menambahkan tampilan permukaan ini di bagian paling akhir skrip

plus sa all




Sekarang kita akan melakukan shift lain, sekarang sepanjang sumbu Y sebesar 0,05 meter, mengembangkan semua garis yang dibentuk oleh perpindahan oleh 5 segmen.

swep surfaces swepsurface tra 0.0 0.05 0.0 5

Dapatkan sesuatu dalam semangat



Gambar yang dihasilkan dapat diputar dengan menahan tombol kiri mouse, dan menghapus tampilan titik dan garis, kita akan melihat sesuatu yang dapat dimengerti



Ya ... CalculiX jauh dari konsep visual yang biasa bagi pengguna massa, tetapi kami membangun geometri balok kami.

Geometri, geometri, tetapi untuk pembuatan mesh, kami akan membuat langkah selanjutnya - menghapus semua plot dan perintah plus dan membungkus kode pembuatan geometri dalam perintah seto dan setc, seperti ini

seto beam
pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0
line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25
seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10
seta surfaces s A001 A002 A003 A004
swep surfaces swepsurface tra 0 0.05 0 5
setc beam

Sepasang perintah ini menggabungkan semua geometri yang dibuat ke dalam blok geometri tertentu dengan balok nama. Sekarang grup geometrik ini dapat dilewati melalui generasi mesh, menentukan setelah semua kode perintah di atas

elty beam he8
mesh beam

- Menghasilkan grid yang terdiri dari parallelepipeds (he8) berdasarkan pada geometri bernama balok. Sekarang cetak jala yang dihasilkan ke file

send beam abq

- Output mesh ke file bernama beam.msh dalam format paket ABAQUS FEM (ada paket proprietary seperti perhitungan FEM dan CalculiX memahami formatnya)



Dengan demikian, grid dihasilkan, Anda dapat melihat file beam.msh dan melihat sesuatu seperti ini di sana

*NODE, NSET=Nbeam
1,0.000000000000e+000,0.000000000000e+000,1.000000000000e-001
2,0.000000000000e+000,0.000000000000e+000,9.000000000000e-002
3,0.000000000000e+000,1.000000000000e-002,9.000000000000e-002
4,0.000000000000e+000,1.000000000000e-002,1.000000000000e-001
5,1.000000000000e-002,0.000000000000e+000,1.000000000000e-001
6,1.000000000000e-002,0.000000000000e+000,9.000000000000e-002
7,1.000000000000e-002,1.000000000000e-002,9.000000000000e-002
8,1.000000000000e-002,1.000000000000e-002,1.000000000000e-001
9,0.000000000000e+000,2.000000000000e-002,9.000000000000e-002
10,0.000000000000e+000,2.000000000000e-002,1.000000000000e-001
11,1.000000000000e-002,2.000000000000e-002,9.000000000000e-002
.
.
.
.
*ELEMENT, TYPE=C3D8, ELSET=Ebeam
1, 1, 2, 3, 4, 5, 6, 7, 8
2, 4, 3, 9, 10, 8, 7, 11, 12
3, 10, 9, 13, 14, 12, 11, 15, 16
4, 14, 13, 17, 18, 16, 15, 19, 20
5, 18, 17, 21, 22, 20, 19, 23, 24
6, 5, 6, 7, 8, 25, 26, 27, 28
7, 8, 7, 11, 12, 28, 27, 29, 30
8, 12, 11, 15, 16, 30, 29, 31, 32
9, 16, 15, 19, 20, 32, 31, 33, 34

Rupanya ini adalah daftar simpul elemen grid dengan koordinatnya, diikuti oleh daftar wajah. Untuk membuat semuanya terlihat lebih indah, kami menggunakan mode interaktif CalculiX. Untuk melakukan ini, membiarkan jendela grafik aktif , masukkan perintah berikut secara berurutan

plot f beam

- menampilkan semua wajah geometri

view edge off

- matikan tampilan tepi

view elem

- nyalakan tampilan elemen grid. Kami menyelesaikan input dari setiap perintah dengan menekan Enter, perintah yang dimasukkan ditampilkan di jendela SciTE di kanan bawah, seperti ini



Ya, Anda tidak dapat menyebutnya super nyaman, namun demikian kami mendapatkan gambar dari mesh yang dihasilkan.



Saya perhatikan bahwa semua titik antara yang dibuat saat membuat geometri menjadi simpul jala. Jadi, kami mendapat kisi heksagonal berukuran 100 x 10 x 5 node, dengan ukuran elemen tepi 10 mm. File beam.fbd yang kami buat menggambarkan geometri masalah dan proses pembuatan mesh.

4. Menetapkan batas

Langkah penting dalam penerapan FEM adalah untuk menetapkan batasan pada perpindahan titik struktural, yaitu, dengan mempertimbangkan kendala yang dikenakan padanya. Dalam kasus kami, salah satu ujung balok terjepit, dan dapat diasumsikan bahwa salah satu ujungnya benar-benar diam. Kita perlu memberi tahu pemecah mana node dari mesh FE yang tidak bergerak. Kami menekan F10 ketika file beam.fbd terbuka, tunggu jendela dengan gambar balok muncul



Dalam mode interaktif, masukkan perintah
rot -y
plot n beam

Tim pertama menyebarkan model sehingga sumbu Y berpaling dari kami, yang kedua - termasuk menggambar node (n) dari jala FE. Memindahkan model (memegang tombol mouse kanan) dan menskalakan gambar (memegang roda mouse) kita mendapatkan gambar ini



Sekarang kita perlu memilih semua node yang ingin kita definisikan sebagai tetap. Untuk melakukan ini, kami kembali menggunakan mode entri data interaktif. Kami merekrut tim

qadd fixed

yang mulai membuat satu set node yang disebut fixed. Kursor pada jendela grafik beralih ke mode pemilihan elemen - ditampilkan dalam bentuk panah dengan kotak kecil. Letakkan kursor seperti ini



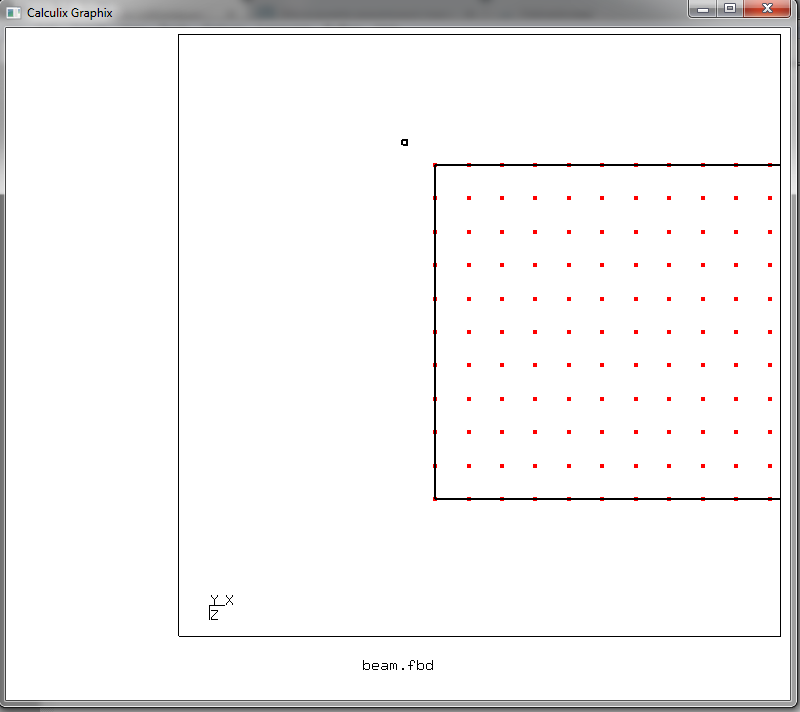
dan tekan tombol r. Dan kemudian kita meletakkan kursor seperti ini



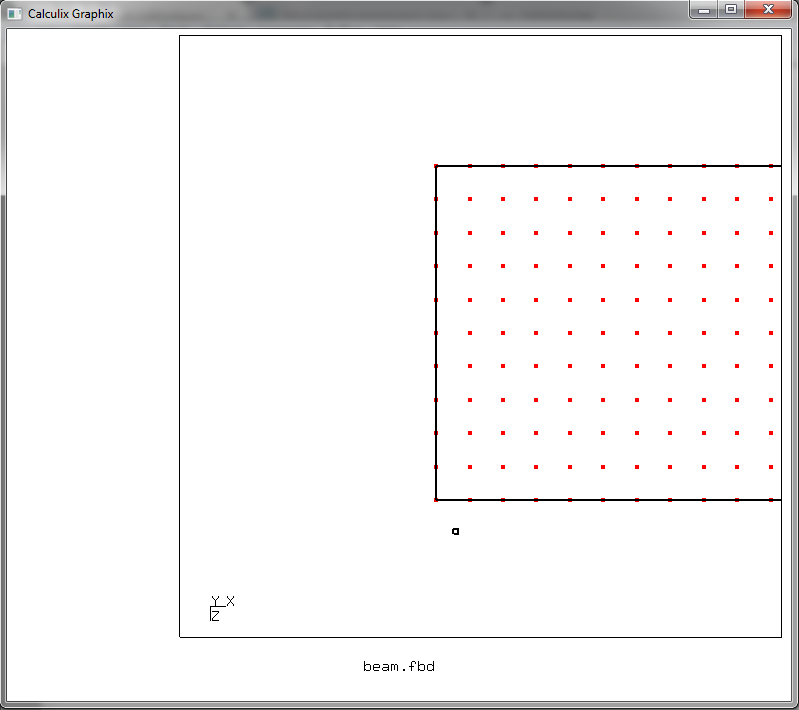
dan tekan r lagi. Jadi, kami membentuk area pemilihan bentuk persegi panjang, diagonal yang ditentukan oleh posisi kursor ditandai dengan menekan r. Kami memilih dengan persegi panjang ini node yang kita butuhkan berbaring di ujung balok



tekan a lalu tekan n, sorot node yang ditandai. Taplak akan muncul di jendela konsol dengan daftar node yang dipilih (gambar dapat diklik)



Masukkan q untuk keluar dari mode dan perintah pemilihan

plus n fixed g

untuk menampilkan node grup tetap berwarna hijau (g). Sekarang kita bisa melihat node mana yang akan dimasukkan dalam kondisi pinning.



Sekarang kita harus membongkar node ini sebagai file kendala, yang selanjutnya diumpankan ke input pemecah. Untuk melakukan ini, ketik perintah

send fixed abq spc 123

- membongkar grup node tetap dalam bentuk file kendala dalam format ABAQUS (abq), membatasi pergerakan semua node grup dalam semua tiga derajat kebebasan (sumbu 1 X, sumbu 2 Y, sumbu 2, sumbu Z 3). Akibatnya, file fix_123.bou terbentuk, dengan konten berikut

** BOUNDARY based on fixed
1, 1, ,
2, 1, ,
3, 1, ,
4, 1, ,
9, 1, ,
10, 1, ,
13, 1, ,
14, 1, ,
17, 1, ,
.
.
.


- pada kenyataannya, ini adalah penghitungan semua node dan tingkat jumlah kebebasan dimana pergerakan dari node yang diberikan terbatas.

5. Penugasan beban

Setelah kami mengamankan balok kami, kami akan mencoba memuatnya. Nyalakan kembali tampilan wajah dan elemen

plot f beam
view edge off
view elem

Arahkan gambar sehingga kita dapat melihat bagian atas ujung balok yang longgar



Mari kita beralih ke mode pemilihan objek

qadd load

Tempatkan kursor pada wajah yang diinginkan dan tekan f



Wajah disorot dalam warna ungu, dan deskripsi muncul di jendela konsol yang ditambahkan ke set beban.

qadd load
2541 e:3873 s:6 n= 5298 5310 5312 5300

Tekan a untuk mengakhiri pembentukan set, tekan q untuk keluar dari mode pemilihan. Kami menerapkan tekanan pada wajah yang dipilih yang memberikan gaya resultan 10.000 N. Mudah untuk menghitung bahwa area wajah yang dipilih adalah 1 cm ² , yang berarti tekanan yang diinginkan adalah 10 ⁸ Pa. Atur pemuatan ini dengan perintah

send load abq pres 1e8

- Menampilkan beban dalam file load.dlo dalam format ABAQUS. File terlihat seperti ini

** Pressure based on load
3873, P6, 100000000.000000

Jumlah elemen mesh, wajahnya dan nilai tekanan pada wajah ini ditunjukkan. Dengan demikian, persiapan data awal dapat dianggap selesai.

6. Deskripsi data input dan peluncuran solver

Semua data itu - kisi, batasan, dan beban, sekarang harus ditarik ke input pemecah FEM, yang kami bentukkan file input semacam ini

beam.inp
*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh
*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou
*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL
*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP


Saya akan menjelaskan lebih detail apa itu. Bagian pertama file

*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh

mengatur deskripsi tugas dan menyertakan file dengan CE-mesh beam.msh. Bagian selanjutnya membentuk syarat batas - hubungan yang kita tentukan di file fixed_123.bou

*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou


Kita tidak boleh lupa tentang bahan yang kita tetapkan sebagai elastis, menentukan modulus Young dan rasio Poisson. Kami mengambil nilai rata-rata untuk baja struktural

*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL

Bagian terakhir mengatur jenis tugas - perhitungan pembebanan statis dan beban dari file load.dlo

*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP


Setelah memeriksa bahwa kami memiliki tab di SciTE dengan file beam.inp, tekan Ctrl + F10, dengan demikian meluncurkan solver. Kami mendapatkan informasi yang mengatakan bahwa CalculiX telah menghitung sesuatu untuk kami di sana. Knalpot, agar tidak mengacaukan teks yang saya bawa di bawah spoiler

7. Postprocessing dan analisis keputusan

Hasil yang diperoleh oleh pemecah memerlukan pemrosesan oleh postprocessor. Untuk memanggilnya, tekan Shift + F10 dan dapatkan jendela grafik dengan gambar balok. Klik di sisi kiri jendela ini, di luar bingkai dengan gambar balok dan dapatkan menu



Apa yang menarik minat kita? Tekan di bagian balok - pilih Kumpulan Data -> STRESS. Menu akan hilang, tetapi kami menyebutnya lagi dan pilih Kumpulan Data -> Entitas -> Mises. Hasilnya, mode tegangan setara von Mises dihidupkan.



Jadi - momen kebenaran! Tegangan setara maksimum di bagian balok adalah 117 MPa, yang sedikit berbeda dari hasil kompromi. Tapi! Memecahkan masalah sopromat, kami tidak memperhitungkan tegangan tangensial selama pembengkokan dan geser, tetapi hanya menghitung tegangan normal dari pembengkokan. Apa yang akan terjadi pada defleksi? Buka menu: Kumpulan Data -> DISP dan Kumpulan Data -> Entitas -> D3



Kami mengamati bahwa perpindahan maksimum sesuai dengan ujung balok yang dimuat dan sama dengan 3,96 milimeter! Luar biasa dan berkorelasi dengan perhitungan kami menggunakan integral Mohr.

Dengan manipulasi sederhana, yang dapat dibaca di sini , animasi deformasi balok juga dihasilkan.

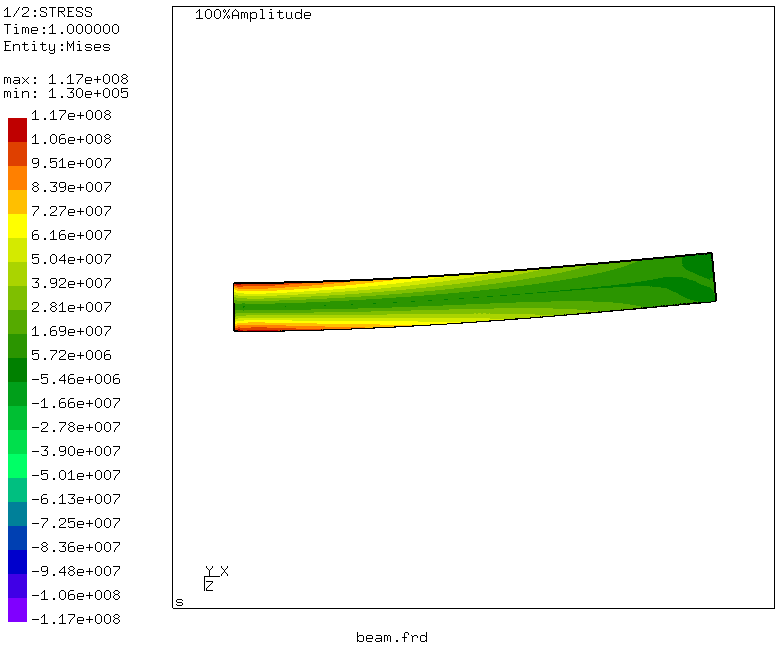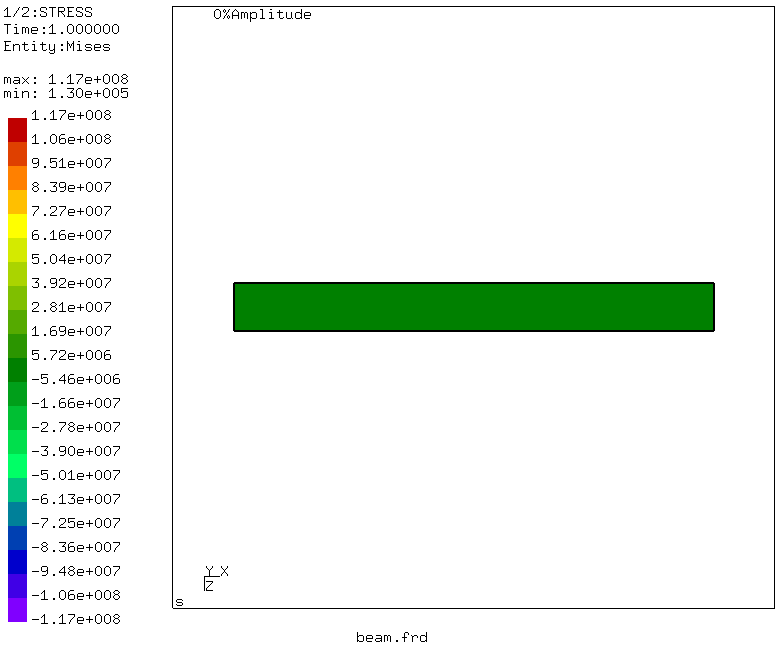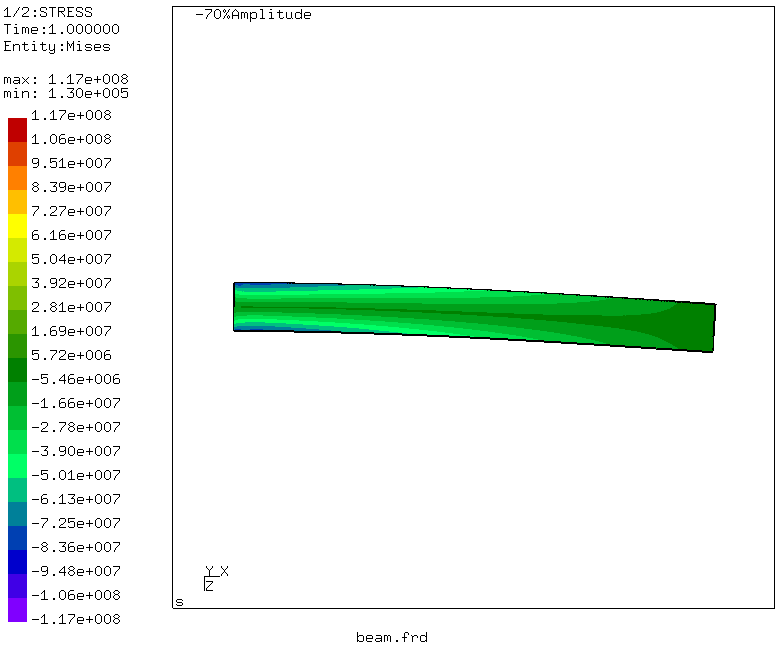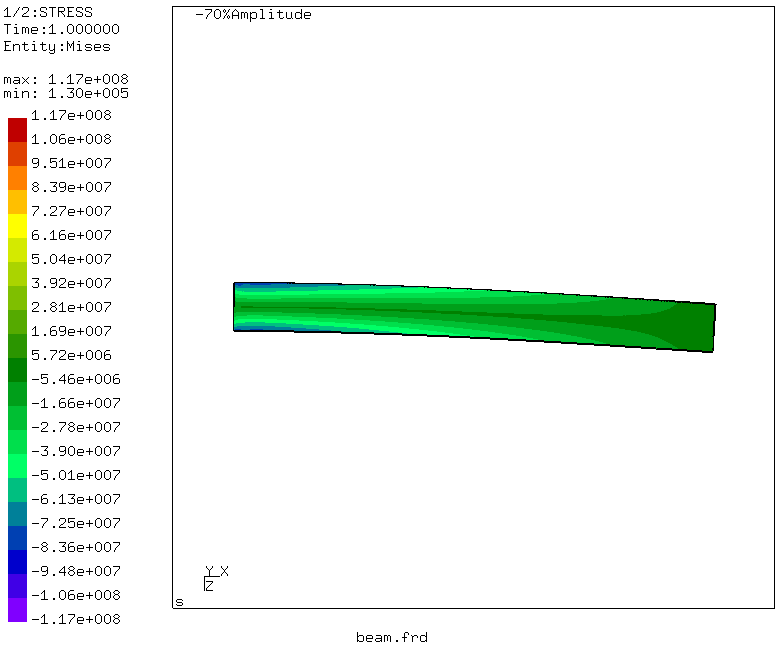
Buat kesimpulan

"Eh, bung, tunggu sebentar, apa selanjutnya?!" Hmm, manusia tidak dapat memasukkan dalam satu artikel seluruh variasi masalah yang muncul ketika menyebutkan FEM secara umum, dan CalculiX pada khususnya. Artikel itu ternyata sangat produktif dan agak membosankan. Dan tujuannya adalah untuk menjelaskan dua hal dalam bahasa yang dapat dipahami:

1. Open Source tidak lulus oleh perangkat lunak analisis FEM
2. Untuk mempelajari dan menggunakan perangkat lunak ini tidak sesulit kelihatannya pada pandangan pertama

Cukup untuk artikel ulasan? Saya kira begitu. Dalam mempersiapkan artikel, sumber-sumber berikut digunakan:

1. Calculix FEA Beam - berfungsi sebagai dasar untuk semua materi yang disajikan. Karena pengalaman yang diperoleh penulis ditambahkan di sini dan semua kode ditulis olehnya selama penulisan artikel, ini bukan terjemahan, yaitu tutorial dalam bahasa Rusia
2. Manual Kalkulus Resmi

Kode contoh tersedia di Gitlab .

Sebagai kesimpulan, saya perhatikan - saya tidak kuat, saya tidak memiliki kompromi di universitas. Beberapa saat kemudian, hidup (dan cinta!) Memaksa saya untuk mengetahui fondasinya. Jadi kesalahan, mungkin, ada dalam teks, tentang yang saya tunggu komentar jahat dan saya berjanji untuk memperhitungkan semua komentar.

Terima kasih atas perhatian anda!