Nomor floating point liar barat tercepat

Dalam proses menerapkan satu "pembaca", masalah muncul dengan peningkatan akurasi perhitungan. Algoritma perhitungan bekerja dengan cepat pada angka floating-point standar, tetapi ketika perpustakaan untuk perhitungan yang akurat terhubung, semuanya mulai melambat liar. Pada artikel ini, kami akan mempertimbangkan algoritma untuk memperluas angka floating-point menggunakan pendekatan multi-komponen, yang memungkinkan untuk mencapai percepatan, karena aritmatika float diimplementasikan pada chip cp. Pendekatan ini akan berguna untuk perhitungan yang lebih akurat dari turunan numerik, inversi matriks, pemangkasan poligon atau masalah geometrik lainnya. Jadi dimungkinkan untuk meniru float 64bit pada kartu video yang tidak mendukungnya.

Pendahuluan

Seperti Nikluas Wirth mewariskan kepada kami untuk menjaga angka 0 dan 1, jadi kami menyimpannya di dalamnya. Dan apakah manusia hidup dalam sistem desimal, dan angka yang tampaknya biasa 0,1 dan 0,3 tidak dapat diwakili dalam sistem biner oleh fraksi terbatas? Kami mengalami kejutan budaya ketika kami menghitungnya. Tentu saja, upaya sedang dilakukan untuk membuat perpustakaan untuk prosesor berdasarkan sistem desimal dan IEEE bahkan memiliki format standar.

Tetapi untuk saat ini, kami memperhitungkan penyimpanan biner di mana-mana dan melakukan semua perhitungan uang dengan perpustakaan untuk perhitungan yang tepat, seperti bignumber, yang menyebabkan hilangnya kinerja. Asiks mempertimbangkan kripto, dan dalam prosesor ada begitu sedikit ruang untuk aritmatika desimal Anda ini, kata pemasar. Oleh karena itu, pendekatan multikomponen, ketika angka disimpan dalam bentuk jumlah angka yang tidak diubah, adalah trik yang mudah dan lingkungan yang aktif berkembang di bidang informatika teoretis. Meskipun Decker masih belajar mengalikan dengan benar, tanpa kehilangan keakuratan, pada tahun 1971, perpustakaan yang siap digunakan muncul jauh kemudian (MPFR, QD) dan tidak dalam semua bahasa, tampaknya karena tidak semua mendukung standar IEEE, tetapi bukti kesalahan perhitungan yang teliti bahkan kemudian, misalnya pada 2017 untuk aritmatika dua kata.

Aritmatika dua kata

Apa gunanya Di masa berjanggut, ketika tidak ada standar untuk angka mengambang, untuk menghindari masalah dengan penerapan pembulatan, Møller muncul, dan Knuth kemudian membuktikan bahwa ada penjumlahan bebas kesalahan. Berlari dengan cara ini

function quickTwoSum(a, b) { let s = a + b; let z = s - a; let e = b - z; return [s, e]; } 

Dalam algoritma ini, diasumsikan bahwa jika $$$| a | > | b |$, maka jumlah pastinya dapat direpresentasikan sebagai jumlah dari dua angka $$$s + e$dan Anda dapat menyimpannya berpasangan untuk perhitungan selanjutnya, dan pengurangan dikurangi menjadi penambahan dengan angka negatif.



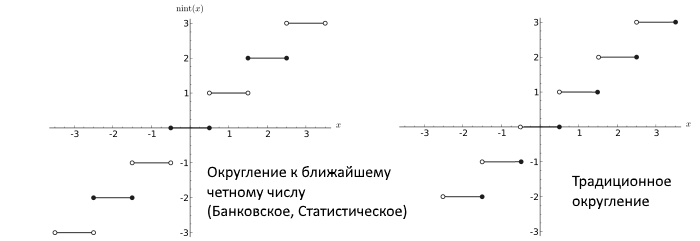
Kemudian, Dekker menunjukkan bahwa jika bilangan floating-point digunakan yang menggunakan pembulatan ke bilangan genap terdekat (pembulatan ke bilangan terdekat dengan genap, yang umumnya merupakan prosedur yang benar, yang tidak mengarah pada kesalahan besar selama perhitungan panjang dan standar IEEE), kemudian ada algoritma multiplikasi bebas kesalahan.

 function twoMult(a, b) { let A = split(a); let B = split(b); let r1 = a * b; let t1 = -r1 + A[0] * B[0]; let t2 = t1 + A[0] * B[1]; let t3 = t2 + A[1] * B[0]; return [r1, t3 + A[1] * B[1]]; } 

di mana split () adalah algoritma Mr. Weltkamp untuk memisahkan angka

 let splitter = Math.pow(2, 27) + 1; function split(a) { let t = splitter * a; let d = a - t; let xh = t + d; let xl = a - xh; return [xh, xl]; } 

menggunakan konstanta $$$C = 2 ^ s + 1$yang menyamakan sedikit lebih dari setengah panjang mantissa, yang tidak mengarah pada jumlah yang melimpah dalam proses penggandaan dan membagi mantissa menjadi dua bagian. Misalnya, dengan panjang kata 64-bit, panjang mantissa adalah 53 dan kemudian s = 27.



Dengan cara ini, Dekker menyediakan himpunan hampir lengkap yang dibutuhkan untuk komputasi dalam aritmatika dua kata. Karena di sana juga ditunjukkan bagaimana mengalikan, membagi, dan kuadrat dua angka dua kata.

Algoritma quickTwoSum-nya untuk menjumlahkan dua kata ganda ada di mana-mana "inline", dan cek digunakan $$$| a | > | b |$. Pada prosesor modern, seperti yang dijelaskan dalam [4], lebih murah untuk menggunakan operasi tambahan dengan angka daripada percabangan algoritma. Oleh karena itu, algoritma berikut ini sekarang lebih tepat untuk menambahkan dua angka kata tunggal

 function twoSum(a, b) { let s = a + b; let a1 = s - b; let b1 = s - a1; let da = a - a1; let db = b - b1; return [s, da + db]; } 

Jadi ini adalah penjumlahan dan penggandaan angka kata ganda.

 function add22(X, Y) { let S = twoSum(X[0], Y[0]); let E = twoSum(X[1], Y[1]); let c = S[1] + E[0]; let V = quickTwoSum(S[0], c); let w = V[1] + E[1]; return quickTwoSum(V[0], w); } function mul22(X, Y) { let S = twoMult(X[0], Y[0]); S[1] += X[0] * Y[1] + X[1] * Y[0]; return quickTwoSum(S[0], S[1]); } 

Secara umum, daftar algoritma yang paling lengkap dan akurat untuk aritmatika kata ganda, batas-batas kesalahan teoretis dan implementasi praktis dijelaskan dalam tautan [3] mulai 2017. Karena itu, jika tertarik, saya sangat merekomendasikan untuk langsung pergi ke sana. Secara umum, algoritma untuk kata quadruple diberikan dalam [6], dan pada [5] untuk ekstensi multikomponen dengan panjang sewenang-wenang. Hanya di sana, setelah setiap operasi, proses renormalisasi digunakan, yang tidak selalu optimal untuk ukuran kecil, dan keakuratan perhitungan dalam QD tidak ditentukan secara ketat. Secara umum, ada baiknya memikirkan batas penerapan dari pendekatan ini, tentu saja.

Cerita horor javascript-a. Perbandingan decimal.js vs bignumber.js vs big.js.

Kebetulan hampir semua perpustakaan untuk perhitungan yang tepat dalam js ditulis oleh satu orang. Ilusi pilihan diciptakan, meskipun semuanya hampir sama. Selain itu, dokumentasi tidak secara eksplisit menunjukkan bahwa jika Anda tidak membulatkan angka setelah setiap operasi perkalian / pembagian, maka ukuran nomor Anda akan berlipat ganda sepanjang waktu, dan kompleksitas algoritme dapat tumbuh menjadi mudah di x3500. Misalnya, perbandingan waktu kalkulasi mereka mungkin terlihat seperti ini jika Anda tidak membulatkan angka.



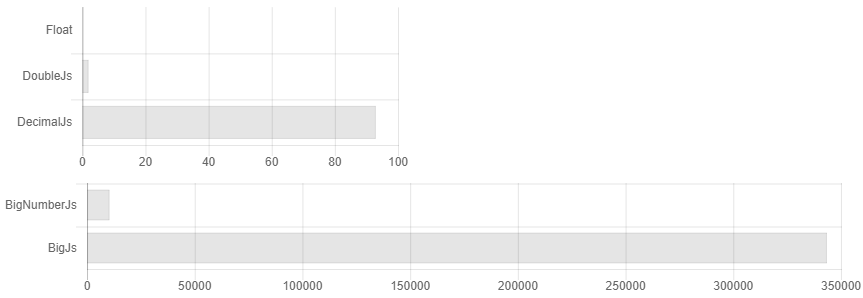
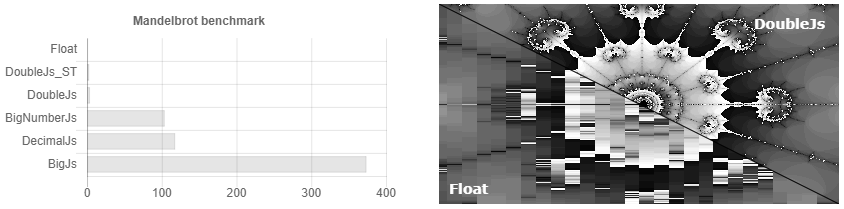
Artinya, Anda menetapkan akurasi ke 32 tempat desimal dan ... Ups, Anda sudah memiliki 64 digit, 128. Kami pikir sangat akurat! 256, 512 ... Tapi saya set 32! .. 1024, 2048 ... Sesuatu seperti ini muncul di atas 3.500 kali. Dokumentasi menyatakan bahwa jika Anda memiliki perhitungan ilmiah, maka mungkin desimal.js lebih baik untuk Anda. Meskipun pada kenyataannya, jika Anda hanya membulatkan secara berkala, untuk perhitungan ilmiah Bignumber.js bekerja sedikit lebih cepat (lihat Gambar 1). Siapa yang perlu menghitung seperseratus sen jika mereka tidak dapat diberikan sebagai ganti? Apakah ada kasus ketika saya perlu menyimpan lebih banyak angka yang ditunjukkan dan tidak dapat keluar dengan beberapa karakter tambahan? Bagaimana cara mengambil sinus dari nomor monster seperti itu, ketika tidak ada yang tahu ketepatan konvergensi dari seri Taylor untuk angka acak? Secara umum, tidak ada kecurigaan tidak berdasar bahwa adalah mungkin untuk meningkatkan kecepatan perhitungan di sana, menggunakan algoritma multiplikasi Schoenhage-Strassen dan menemukan sinus dengan perhitungan Cordic, misalnya.

Double.js

Saya ingin mengatakan, tentu saja, bahwa Double.js menghitung dengan cepat dan akurat. Tapi ini tidak sepenuhnya benar, yaitu 10 kali lebih cepat dari yang dipertimbangkan, tetapi tidak selalu akurat. Misalnya, 0,3-0,1 dapat diproses, melewati penyimpanan ganda dan sebaliknya. Tetapi nomor Pi dapat diselesaikan dengan akurasi ganda hampir 32 digit dan itu tidak berhasil. Kesalahan dihasilkan pada tanggal 16, seolah-olah terjadi overflow. Secara umum, saya mendesak komunitas js untuk bekerja bersama untuk mencoba menyelesaikan masalah parsing, karena saya mandek. Saya mencoba mengurai secara digital dan membaginya dalam presisi ganda, seperti pada QD, membagi dalam batch 16 digit dan membaginya dalam presisi ganda, membagi mantissa menggunakan Big.js seperti pada salah satu lib Julia. Sekarang saya berdosa pada bug di .parseFloat (), karena standar IEEE dengan pembulatan ke integer terdekat didukung bahkan dengan ECMAScript 1. Meskipun tentu saja Anda dapat mencoba untuk mengikat buffer biner dan menonton setiap 0 dan 1. Secara umum, jika Anda dapat menyelesaikan masalah ini, maka selanjutnya dimungkinkan untuk membuat perhitungan dengan akurasi sewenang-wenang dengan akselerasi di x10-x20 dari bignumber.js. Namun, banyak Mandelbrot yang telah menghasilkan kualitas, dan Anda dapat menggunakannya untuk tugas-tugas geometris.

Setahun kemudian, saya kembali ke sini dan masih memperbaiki masalah dengan parsing. Masalahnya hanya dalam akurasi kurang, ketika dikalikan dengan 10 ^ (- n). Semua algoritma telah direvisi dari awal, dan sekarang dijalankan dengan akurasi dan kecepatan yang menakutkan.



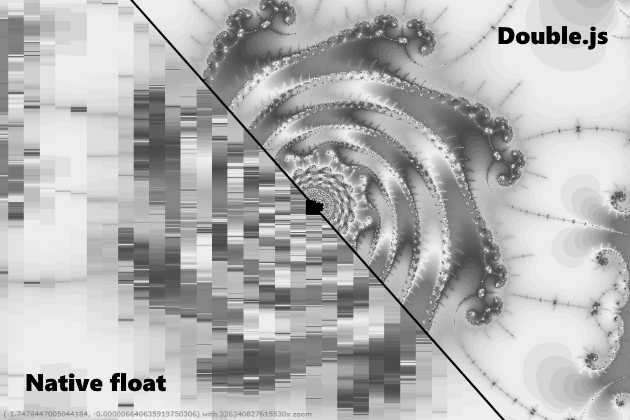
Berikut ini tautan ke lib , ada patokan interaktif dan kotak pasir tempat Anda bisa bermain dengannya.

Sumber yang digunakan

1. O. Møller. Kuasi ganda presisi dalam aritmatika floating-point. , 1965.
2. Theodorus Dekker. Teknik floating-point untuk memperluas presisi yang tersedia , 1971. [ Penampil ]
3. Mioara Joldes, Jean-Michel Muller, Valentina Popescu. Batas kesalahan ketat dan ketat untuk blok bangunan dasar aritmatika kata ganda , 2017. [ PDF ]
4. Muller, J.-M. Brisebarre, N. de Dinechin, dll. Buku Pegangan Aritmatika Titik Apung, Bab 14, 2010.
5. Jonathan Shewchuk. Predikat Geometris Floating-Point Adaptif yang Kuat , 1964. [ PDF ]
6. Yozo Hida, Xiaoye Li, David Bailey. Perpustakaan untuk Aritmatika Double-Double dan Quad-Double , 2000. [ PDF ]