Bagaimana cara menggambar gambar vektor? Bagi saya, seperti bagi banyak orang lain, jawabannya cukup jelas: kemungkinan besar di ilustrator. Baik, atau di Inskape. Saya juga berpikir ketika saya diperintahkan untuk menggambar delapan ratus lembar untuk buku teks fisika. Tidak ada yang seperti itu, hanya ilustrasi teknis hitam dan putih dengan segala macam balok, bola, mata air, lensa, mobil, traktor, dan sejenisnya. Seharusnya buku itu dibuat di latech, dan saya diberi file Word dengan gambar yang disisipkan - baik dalam sketsa pensil, atau pemindaian dari buku-buku lain - dan naskah itu tampaknya dalam beberapa bentuk. Dalam hal ini, pikiran pertama - untuk menggambar di inscape - menyerah pada fantasi pada topik "bagaimana ini akan mengotomatiskan segalanya?" Untuk beberapa alasan,
MetaPost tampaknya menjadi pilihan terbaik saat itu.
Nilai tambah yang paling signifikan dari solusi tersebut adalah bahwa setiap gambar dapat menjadi fungsi kecil dari beberapa variabel; gambar seperti itu mudah, misalnya, untuk mengubah ukuran dan menyesuaikan garis-garis dengan keadaan spesifik yang sebelumnya tidak diketahui tanpa melanggar proporsi penting, yang sulit dicapai dengan cara yang lebih tradisional. Dan elemen berulang - bola dan mata air yang sama - dapat dibuat untuk berperilaku jauh lebih menarik daripada cara yang dimungkinkan oleh editor vektor "manusia".
Saya ingin membuat foto dengan menetas, seperti yang ditemukan di buku-buku lama.

Pertama, kami harus mendapatkan garis ketebalan variabel. Kesulitan utama di sini adalah untuk membangun kurva yang kurang lebih sejajar dengan yang diberikan dan, jika perlu, mengubah jarak ke yang ini. Saya mengandalkan yang paling, mungkin, cara paling primitif di mana segmen yang menghubungkan titik-titik perantara dari kurva Bezier hanya ditransfer pada jarak tertentu secara paralel. Dengan selisih itu jarak ini bisa bervariasi di sepanjang kurva.
Dalam kebanyakan kasus, ini memungkinkan hasil yang layak.
Kode contohSelanjutnya diasumsikan bahwa perpustakaan telah
diunduh dan di suatu tempat terdapat jalur
input fiziko.mp; . Cara tercepat untuk memulai dan mencari di ConTeXt (maka
beginfig dan
endfig tidak diperlukan):
\starttext
\startMPcode
input fiziko.mp;
\stopMPcode
\stoptext
atau di LuaLaTeX:
\documentclass{article}
\usepackage{luamplib}
\begin{document}
\begin{mplibcode}
input fiziko.mp;
\end{mplibcode}
\end{document}
beginfig(3);
path p, q; % , , ,
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q := offsetPath(p)(1cm*sin(offsetPathLength*pi)); % — , — (offsetPathLength, 0 1), ,
draw p;
draw q dashed evenly;
endfig;
Sekarang dua kurva ini dapat digunakan untuk membuat garis garis ketebalan yang bervariasi.

Kode contohbeginfig(4);
path p, q[];
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q1 := offsetPath(p)(1/2pt*(sin(offsetPathLength*pi)**2)); %
q2 := offsetPath(p)(-1/2pt*(sin(offsetPathLength*pi)**2)); %
fill q1--reverse(q2)--cycle;
endfig;
Ketebalan harus agak dibatasi dari bawah, jika tidak raster akan mengambil bagian garis yang terlalu tipis saat mencetak, dan ini biasanya tidak terlalu indah. Salah satu pilihan adalah menggambar semua garis, ketebalan yang kurang dari nilai tertentu, dengan garis putus-putus dengan ketebalan minimum yang sama, sehingga jumlah total cat per satuan panjang rata-rata sesuai dengan garis ketebalan target. Artinya, alih-alih mengurangi jumlah cat dari sisi garis, mulailah mengunyahnya dengan garis-garis melintang.

Kode contohbeginfig(5);
path p;
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
draw brush(p)(1pt*(sin(offsetPathLength*pi)**2)); % , ,
endfig;
Sekarang kamu bisa menggambar bola. Itu bisa saja lingkaran konsentris, ketebalan garis yang ditentukan oleh fungsi penerangan bola pada titik-titik yang dilewati garis tersebut.
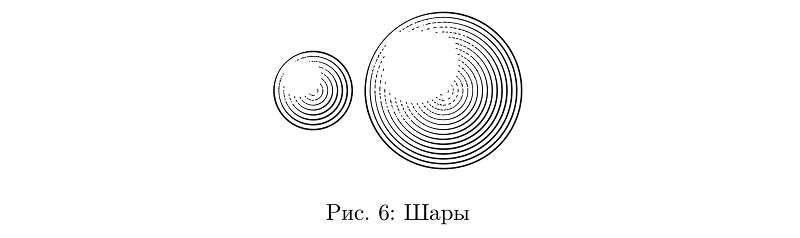
Kode contohbeginfig(6);
draw sphere.c(1.2cm);
draw sphere.c(2.4cm) shifted (2cm, 0);
endfig;
Primitif lain yang mudah digunakan adalah "selang": silinder yang dapat ditekuk dengan cara apa pun. Selama mereka adalah penampang yang konstan, semuanya sederhana dengan mereka.
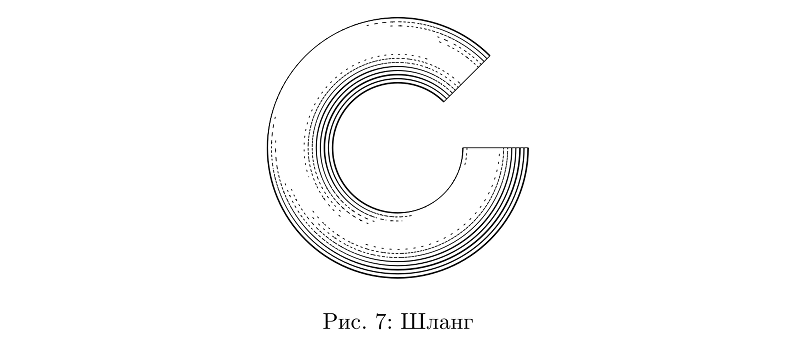
Kode contohbeginfig(7);
path p;
p := subpath (1,8) of fullcircle scaled 3cm;
draw tube.l(p)(1/2cm); % — ,
endfig;
Jika ketebalan berubah, maka jumlah goresan harus diubah sesuai, sambil mempertahankan kerapatan isian rata-rata tidak berubah, dan juga memperhitungkan perubahan ketebalan saat menghitung iluminasi.
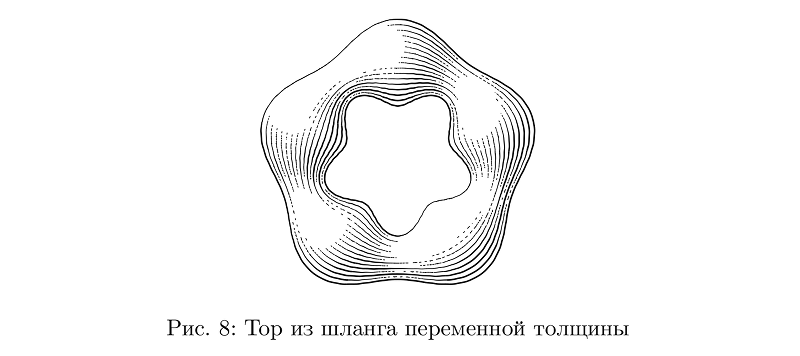
Kode contohbeginfig(8);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.l(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Masih ada selang dengan penetasan melintang, tetapi bagi mereka itu lebih sulit untuk memecahkan masalah menjaga kepadatan rata-rata pengisian, sehingga dalam banyak kasus mereka masih tidak terlihat sangat baik.
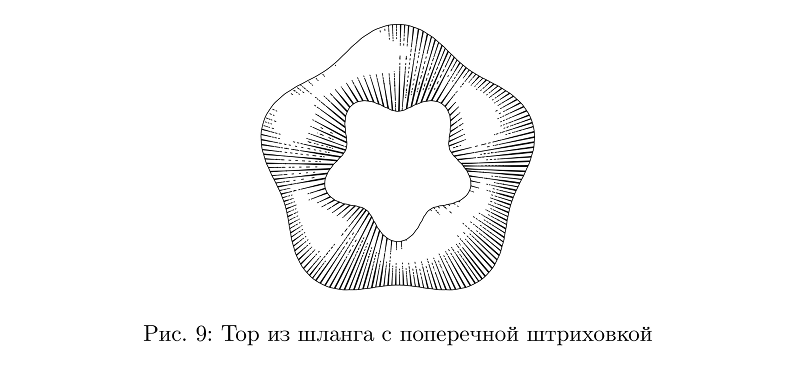
Kode contohbeginfig(9);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.t(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Pada prinsipnya, banyak hal dapat dibuat dari selang saja: dari kerucut dan silinder ke langkan.
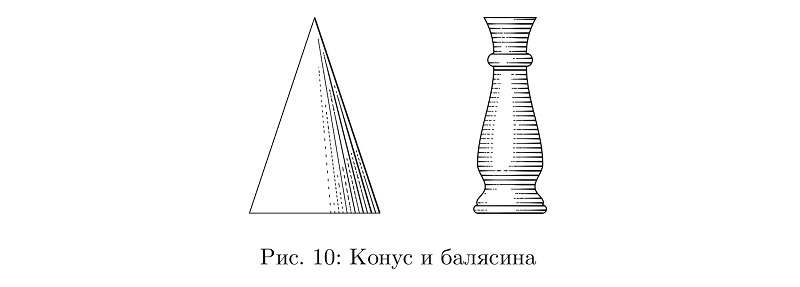
Kode contohbeginfig(10);
draw tube.l ((0, 0) -- (0, 3cm))((1-offsetPathLength)*1cm) shifted (-3cm, 0); %
path p;
p := (-1/2cm, 0) {dir(175)} .. {dir(5)} (-1/2cm, 1/8cm) {dir(120)} .. (-2/5cm, 1/3cm) .. (-1/2cm, 3/4cm) {dir(90)} .. {dir(90)}(-1/4cm, 9/4cm){dir(175)} .. {dir(5)}(-1/4cm, 9/4cm + 1/5cm){dir(90)} .. (-2/5cm, 3cm); %
p := pathSubdivide(p, 6);
draw p -- reverse(p xscaled -1) -- cycle;
tubeGenerateAlt(p, p xscaled -1, p rotated -90); % , tube.t, — — , — .
endfig;
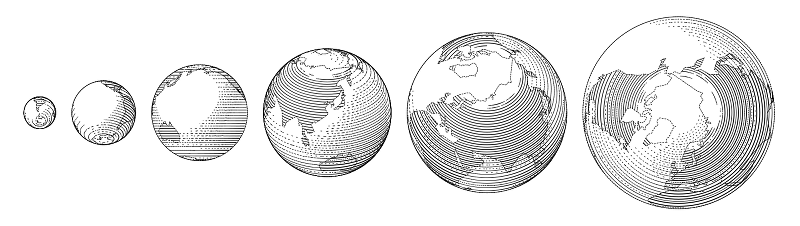
Beberapa yang dapat dibangun dari bagian-bagian tersebut ada di perpustakaan. Katakanlah bola dunia pada dasarnya adalah bola.
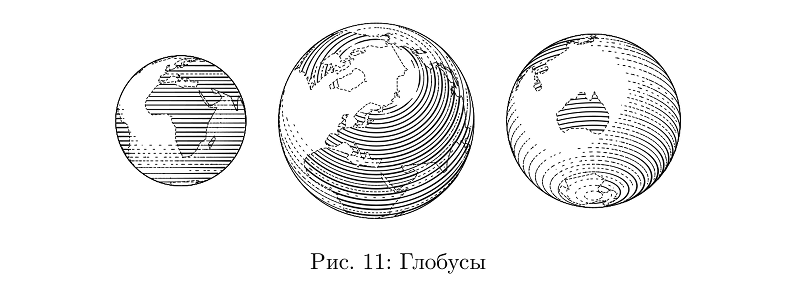
Kode contohbeginfig(11);
draw globe(1cm, -15, 0) shifted (-6/2cm, 0); % , ,
draw globe(3/2cm, -30.28367, 59.93809);
draw globe(4/3cm, -140, -30) shifted (10/3cm, 0);
endfig;
Meskipun tidak: di sini penetasan berjalan secara paralel, dan mengendalikan ketebalan goresan untuk mempertahankan kerapatan isian bahkan lebih sulit daripada dalam kasus penetasan melintang pada selang, jadi ini adalah jenis bola yang terpisah.
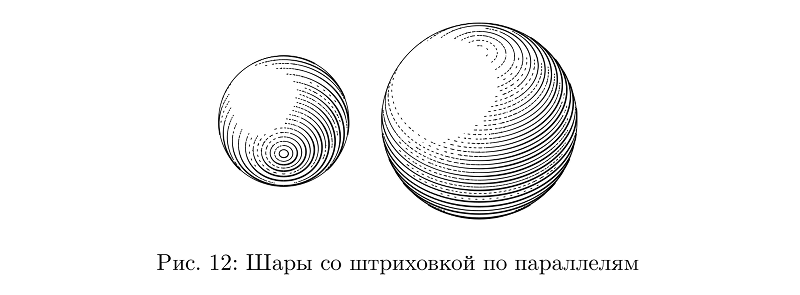
Kode contohbeginfig(12);
draw sphere.l(2cm, -60); %
draw sphere.l(3cm, 45) shifted (3cm, 0);
endfig;
Dan beratnya adalah desain langsung dari dua jenis selang dengan ketebalan bervariasi.
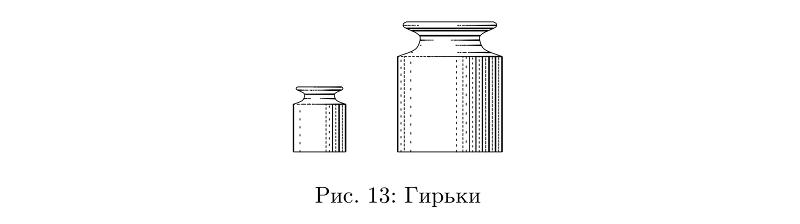
Kode contohbeginfig(13);
draw weight.s(1cm); %
draw weight.s(2cm) shifted (2cm, 0);
endfig;
Masih ada alat untuk mengikat selang menjadi simpul.
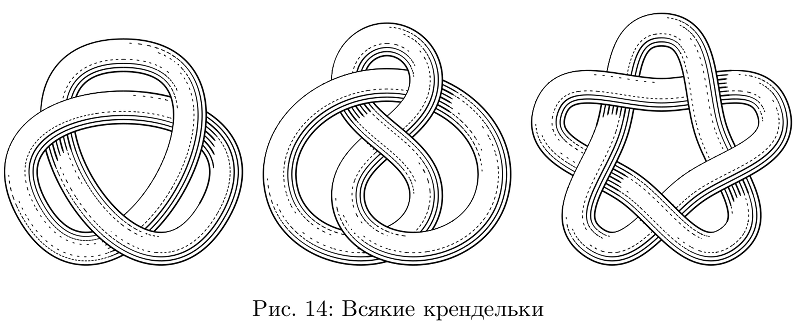
Kode sampel agar tidak berantakan, hanya satu simpulbeginfig(14);
path p;
p := (dir(90)*4/3cm) {dir(0)} .. tension 3/2 ..(dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2 ..(dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2 .. cycle;
p := p scaled 6/5;
addStrandToKnot (primeOne) (p, 1/4cm, "l", "1, -1, 1"); % primeOne , p 1/4cm, "l" ( tube.l, tube.t ) «» "1, -1, 1" p
draw knotFromStrands (primeOne); % .
endfig;
Bayangan node adalah beberapa komplikasi dalam model pencahayaan. Pada prinsipnya, tidak ada yang mengganggu untuk menggunakannya dalam kasus lain, tapi saya tidak menetapkan tujuan untuk masuk jauh ke dalam volume, jadi sementara ini tidak terlalu nyaman, itu tidak bekerja di mana-mana.
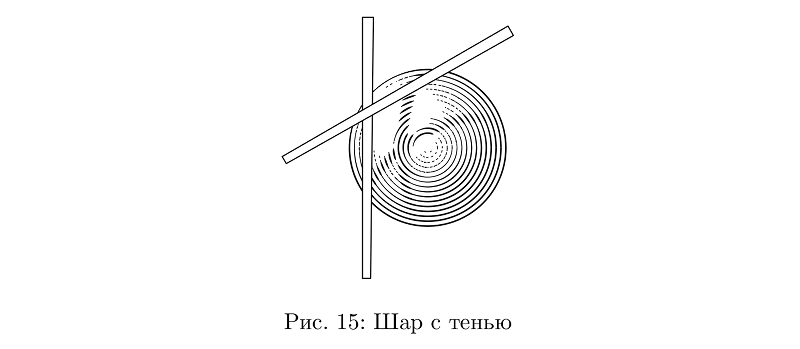
Kode contohbeginfig(15);
path shadowPath[];
boolean shadowsEnabled;
numeric numberOfShadows;
shadowsEnabled := true; %
numberOfShadows := 1; %
shadowPath0 := (-1cm, -2cm) -- (-1cm, 2cm) -- (-1cm +1/6cm, 2cm) -- (-1cm + 1/8cm, -2cm) -- cycle; % , ,
shadowDepth0 := 4/3cm; % - «» ,
shadowPath1 := shadowPath0 rotated -60;
shadowDepth1 := 4/3cm;
draw sphere.c(2.4cm); % sphere.c tube.l
fill shadowPath0 withcolor white;
draw shadowPath0;
fill shadowPath1 withcolor white;
draw shadowPath1;
endfig;
Dan, tentu saja, Anda membutuhkan tekstur kayu. Pengaruh sifat pertumbuhan simpul pada pola bagian-bagian cincin pohon adalah topik untuk penelitian serius. Sangat menyederhanakan, kita bisa membayangkan cincin tahunan dalam bidang paralel yang menjadi tempat distorsi knot. Jadi cukup untuk menggambarkan perubahan pada bidang dengan beberapa fungsi yang tidak terlalu canggih (fungsi simpul) dan mempertimbangkan serangkaian isolin untuk jumlah himpunan fungsi seperti pola cincin pohon yang diinginkan.
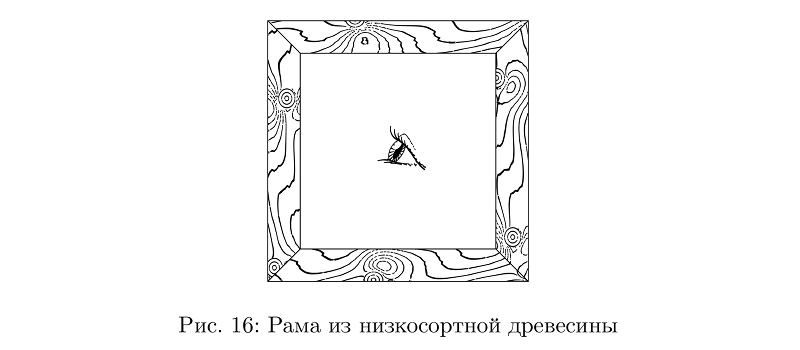
Kode contohbeginfig(16);
numeric w, b;
pair A, B, C, D, A', B', C', D';
w := 4cm;
b := 1/2cm;
A := (0, 0);
A' := (b, b);
B := (0, w);
B' := (b, wb);
C := (w, w);
C' := (wb, wb);
D := (w, 0);
D' := (wb, b);
draw woodenThing(A--A'--B'--B--cycle, 0); % , A--A'--B'--B--cycle, 0
draw woodenThing(B--B'--C'--C--cycle, 90);
draw woodenThing(C--C'--D'--D--cycle, 0);
draw woodenThing(A--A'--D'--D--cycle, 90);
eyescale := 2/3cm; %
draw eye(150) shifted 1/2[A,C]; % 150
endfig;
Mata dari gambar di atas bisa sedikit terbuka, lalu menyipit, dan lebar pupil berubah. Tidak ada makna khusus dalam hal ini, tetapi ternyata lebih jelas daripada jika hal-hal sepele itu secara mekanis sama di mana-mana.

Kode contohbeginfig(17);
eyescale := 2/3cm; % 1/2cm
draw eye(0) shifted (0cm, 0);
draw eye(0) shifted (1cm, 0);
draw eye(0) shifted (2cm, 0);
draw eye(0) shifted (3cm, 0);
draw eye(0) shifted (4cm, 0);
endfig;
Paling sering, gambar-gambar itu tidak terlalu rumit, tetapi jika Anda mendekati masalah ini dengan sangat serius, maka banyak tugas yang perlu diselesaikan untuk menggambarkannya secara bermakna. Di sini, katakanlah, tugas Lopital tentang blok (saya tidak tahu bagaimana itu disebut dalam bahasa Rusia dengan benar, itu tidak ada dalam buku teks, itu hanya sebagai contoh): blok tergantung pada tali yang panjangnya l ditangguhkan pada titik A, itu dikaitkan pada tali lain tergantung pada ketinggian yang sama di titik B, kargo C tergantung pada tali kedua.Pertanyaannya adalah, jika tali dan blok tidak berat, di mana kargo akan? Anehnya, baik solusi dari masalah dan konstruksinya tidak terlalu mendasar, tetapi, bermain dengan beberapa variabel, Anda dapat dengan mudah membuat gambar persis apa yang akan terlihat terbaik di strip, sambil tetap benar.
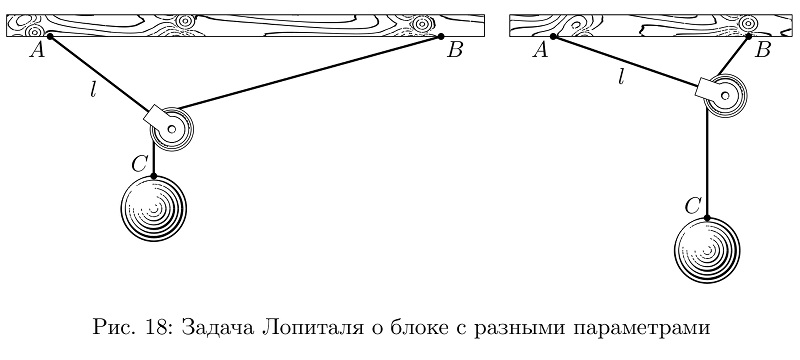
Kode contohvardef lHopitalPulley (expr AB, l, m) = % AB l, m . ? : , , arithmetic overflow.
save A, B, C, D, E, o, a, x, y, d, w, h, support;
image(
pair A, B, C, D, E, o[];
path support;
numeric a, x[], y[], d[], w, h;
x1 := (l**2 + abs(l)*((sqrt(8)*AB)++l))/4AB; % ,
y1 := l+-+x1; %
y2 := m - ((AB-x1)++y1); %
A := (0, 0);
B := (AB*cm, 0);
D := (x1*cm, -y1*cm);
C := D shifted (0, -y2*cm);
d1 := 2/3cm; d2 := 1cm; d3 := 5/6d1; % ,
w := 2/3cm; h := 1/3cm; % . ,
o1 := (unitvector(CD) rotated 90 scaled 1/2d3);
o2 := (unitvector(DB) rotated 90 scaled 1/2d3);
E := whatever [D shifted o1, C shifted o1]
= whatever [D shifted o2, B shifted o2]; % ,
a := angle(AD);
support := A shifted (-w, 0) -- B shifted (w, 0) -- B shifted (w, h) -- A shifted (-w, h) -- cycle;
draw woodenThing(support, 0); % ,
draw pulley (d1, a - 90) shifted E; %
draw image(
draw A -- D -- B withpen thickpen;
draw D -- C withpen thickpen;
) maskedWith (pulleyOutline shifted E); %
draw sphere.c(d2) shifted C shifted (0, -1/2d2); %
dotlabel.llft(btex $A$ etex, A);
dotlabel.lrt(btex $B$ etex, B);
dotlabel.ulft(btex $C$ etex, C);
label.llft(btex $l$ etex, 1/2[A, D]);
)
enddef;
beginfig(18);
draw lHopitalPulley (6, 2, 11/2); % ,
draw lHopitalPulley (3, 5/2, 3) shifted (8cm, 0);
endfig;
Apa itu buku teks? Sayang dan ah, ketika hampir semua ilustrasi dan tata letak sudah siap, sesuatu terjadi di sana dan dia tidak pernah keluar. Karena itu, mungkin, beberapa waktu kemudian, saya menulis ulang semua hal utama dari pustaka yang dihasilkan lagi dan
memposting kode pada github . Beberapa kunshtyuki tidak masuk ke sana: misalnya, sirkuit listrik atau fungsi untuk menggambar mobil dan traktor. Beberapa ditambahkan: node, misalnya.
Seluruh dapur ini tidak bekerja dengan cepat: dibutuhkan sekitar satu menit untuk mengumpulkan semua gambar untuk artikel ini dengan LuaLaTeX di laptop saya dengan i5-4200U 1,6 GHz. Untuk banyak hal, generator angka pseudo-acak digunakan, sehingga gambar yang mirip akan terlihat sedikit berbeda tidak hanya di dalam satu run (ini adalah fitur), tetapi setiap run berikutnya akan memberikan gambar yang berbeda dari yang sebelumnya. Tetapi Anda selalu dapat mengatur
randomseed := - di pembukaan, dan semua proses yang sama akan menghasilkan gambar yang sama.