Bahkan, dia yang paling. Tetapi hal pertama yang pertama.
Pernyataan masalah
Saya menguasai python, menyelesaikan semuanya di Codewars. Saya menemukan tugas terkenal tentang gedung pencakar langit dan telur. Satu-satunya perbedaan adalah bahwa sumber data bukan 100 lantai dan 2 telur, tetapi lebih sedikit.
Diberikan: N telur, M mencoba untuk melemparkannya, gedung pencakar langit tanpa akhir.
Tentukan: lantai maksimum tempat Anda bisa melempar telur tanpa merusaknya. Telur berbentuk bulat dalam ruang hampa dan, jika salah satunya tidak pecah, jatuh, misalnya, dari lantai 99, maka yang lain juga akan tahan jatuh dari semua lantai kurang dari seperseratus.
0 <= N, M <= 20.000.
Jangka waktu dua lusin tes adalah 12 detik.
Cari solusinya
Kita perlu menulis tinggi fungsi (n, m), yang akan mengembalikan nomor lantai untuk n, m yang diberikan. Karena itu akan sangat sering disebutkan, dan setiap kali Anda menulis "tinggi" kemalasan, maka di mana-mana, kecuali kode, saya akan menyebutnya sebagai f (n, m).
Mari kita mulai dengan nol. Jelas, jika tidak ada telur atau upaya untuk melemparkannya, maka tidak ada yang dapat ditentukan dan jawabannya akan nol.
f (0, m) = 0, f (n, 0) = 0.Misalkan ada satu telur, dan ada 10 upaya. Anda dapat mengambil risiko segalanya dan langsung membuangnya dari lantai seratus, tetapi jika gagal, Anda tidak akan dapat menentukan apa pun, jadi lebih logis untuk memulai dari lantai pertama dan naik satu lantai setelah setiap lemparan, sampai upaya atau telur berakhir. Maksimum yang bisa Anda dapatkan jika telur tidak gagal adalah lantai nomor 10.
f (1, m) = mAmbil telur kedua, coba lagi 10. Sekarang, maka Anda bisa mengambil kesempatan dengan yang keseratus? Jika rusak, akan ada satu upaya lagi dan 9, setidaknya 9 lantai akan dapat lulus. Jadi mungkin Anda perlu mengambil risiko bukan dari keseratus, tetapi dari kesepuluh? Masuk akal. Kemudian, jika berhasil, 2 telur dan 9 upaya akan tetap. Dengan analogi, sekarang Anda perlu naik 9 lantai lagi. Dengan serangkaian keberhasilan - 8, 7, 6, 5, 4, 3, 2 dan 1 lainnya. Total, kami berada di lantai 55 dengan dua telur utuh dan tanpa berusaha. Jawabannya adalah jumlah anggota M pertama dari perkembangan aritmatika dengan anggota pertama 1 dan langkah 1.
f (2, m) = (m * m + m) / 2 . Juga jelas bahwa pada setiap langkah fungsi f (1, m) dipanggil, tetapi ini belum akurat.
Lanjutkan dengan tiga telur dan sepuluh upaya. Dalam hal lemparan pertama yang gagal, lantai ditutupi oleh 2 telur dan 9 upaya akan ditutup dari bawah, yang berarti lemparan pertama harus dilakukan dari lantai f (2, 9) + 1. Kemudian, jika berhasil, kami memiliki 3 telur dan 9 upaya . Dan untuk upaya kedua Anda harus naik f (2,8) + 1 lantai lain. Demikian seterusnya, hingga 3 butir telur dan 3 upaya tersisa di tangan. Dan kemudian sudah waktunya untuk terganggu dengan mempertimbangkan kasus dengan N = M, ketika ada banyak telur karena ada upaya.
Dan pada saat yang sama ketika ada lebih banyak telur.Tapi di sini semuanya jelas - telur di luar yang pecah tidak akan berguna bagi kita, bahkan jika setiap lemparan tidak berhasil. f (n, m) = f (m, m) jika n> m . Dan semuanya, 3 butir telur, 3 kali lemparan. Jika telur pertama pecah, maka Anda dapat memeriksa f (2, 2) lantai ke bawah, dan jika tidak pecah, maka f (3,2) lantai ke atas, yaitu, f yang sama (2, 2). Total f (3, 3) = 2 * f (2, 2) + 1 = 7. Dan f (4, 4), secara analogi, akan terdiri dari dua f (3, 3) dan satu, dan itu akan menjadi 15. Semua itu menyerupai kekuatan dua, dan kami menulis: f (m, m) = 2 ^ m - 1 .
Ini terlihat seperti pencarian biner di dunia fisik: kita mulai dari lantai nomor 2 ^ (m-1), jika sukses, kita naik 2 ^ (m-2) lantai ke atas, dan jika terjadi kegagalan, kita turun sebanyak yang turun, dan, sampai upaya habis. Dalam kasus kami, kami bangkit setiap saat.
Mari kita kembali ke f (3, 10). Bahkan, pada setiap langkah, semuanya berujung pada jumlah f (2, m-1) - jumlah lantai yang dapat ditentukan jika terjadi kegagalan, unit dan f (3, m-1) - jumlah lantai yang dapat ditentukan jika sukses. Dan menjadi jelas bahwa dari peningkatan jumlah telur dan upaya tidak mungkin ada yang berubah.
f (n, m) = f (n - 1, m - 1) + 1 + f (n, m - 1) . Dan ini adalah formula universal yang dapat diimplementasikan dalam kode.
from functools import lru_cache @lru_cache() def height(n,m): if n==0 or m==0: return 0 elif n==1: return m elif n==2: return (m**2+m)/2 elif n>=m: return 2**n-1 else: return height(n-1,m-1)+1+height(n,m-1)
Tentu saja, sebelumnya saya menginjak fungsi rekursif non-memoising dan menemukan bahwa f (10, 40) membutuhkan waktu hampir 40 detik dengan jumlah panggilan untuk dirinya sendiri - 97806983. Tetapi memoisasi juga hanya menghemat pada interval awal. Jika f (200.400) dieksekusi dalam 0,8 detik, maka f (200, 500) sudah dalam 31 detik. Lucu ketika mengukur runtime menggunakan% timeit, hasilnya jauh lebih sedikit daripada yang asli. Jelas, menjalankan fungsi pertama kali mengambil sebagian besar waktu, sedangkan sisanya hanya menggunakan hasil memoisasi itu. Kebohongan, kebohongan yang mencolok, dan statistik.
Rekursi tidak diperlukan, kami melihat lebih jauh
Jadi, dalam tes, misalnya, f (9477, 10000) muncul, tetapi f menyedihkan saya (200, 500) tidak lagi cocok pada waktu yang tepat. Jadi ada solusi lain, tanpa rekursi, kami akan melanjutkan pencariannya. Saya menambahkan kode dengan menghitung panggilan fungsi dengan parameter tertentu untuk melihat apa yang akhirnya diuraikan menjadi. Selama 10 upaya, hasil berikut diperoleh:
f (3.10) = 7+ 1 * f (2.9) + 1 * f (2.8) + 1 * f (2.7) + 1 * f (2.6) + 1 * f (2 , 5) + 1 * f (2,4) + 1 * f (2,3) + 1 * f (3,3)
f (4.10) = 27+ 1 * f (2.8) + 2 * f (2.7) + 3 * f (2.6) + 4 * f (2.5) + 5 * f (2 , 4) + 6 * f (2,3) + 6 * f (3,3) + 1 * f (4,4)
f (5.10) = 55+ 1 * f (2.7) + 3 * f (2.6) + 6 * f (2.5) + 10 * f (2.4) + 15 * f (2 , 3) + 15 * f (3.3) + 5 * f (4.4) + 1 * f (5.5)
f (6.10) = 69+ 1 * f (2.6) + 4 * f (2.5) + 10 * f (2.4) + 20 * f (2.3) + 20 * f (3 , 3) + 10 * f (4.4) + 4 * f (5.5) + 1 * f (6.6)
f (7,10) = 55+ 1 * f (2,5) + 5 * f (2,4) + 15 * f (2,3) + 15 * f (3,3) + 10 * f (4 , 4) + 6 * f (5.5) + 3 * f (6.6) + 1 * f (7.7)
f (8,10) = 27+ 1 * f (2,4) + 6 * f (2,3) + 6 * f (3,3) + 5 * f (4,4) + 4 * f (5 , 5) + 3 * f (6,6) + 2 * f (7,7) + 1 * f (8,8)
f (9,10) = 7+ 1 * f (2,3) + 1 * f (3,3) + 1 * f (4,4) + 1 * f (5,5) + 1 * f (6 , 6) + 1 * f (7,7) + 1 * f (8,8) + 1 * f (9,9)
Beberapa keteraturan terlihat:

Koefisien ini dihitung secara teoritis. Setiap biru adalah jumlah bagian atas dan kiri. Dan warna ungu adalah warna biru yang sama, hanya dalam urutan terbalik. Anda dapat menghitung, tetapi ini adalah rekursi lagi, dan di dalamnya saya kecewa. Kemungkinan besar, banyak (disayangkan bukan saya) telah mempelajari angka-angka ini, tetapi untuk sekarang saya akan menyimpan intrik, mengikuti solusi saya sendiri. Saya memutuskan untuk meludahi mereka dan pergi ke sisi lain.
Dia membuka exel, membangun piring dengan hasil fungsi, dan mulai mencari pola. C3 = IF (C $ 2> $ B3; 2 ^ $ B3-1; C2 + B2 + 1), di mana $ 2 adalah baris dengan jumlah telur (1-13), $ B adalah kolom dengan jumlah upaya (1-20), C3 - sel di persimpangan dua telur dan satu upaya.
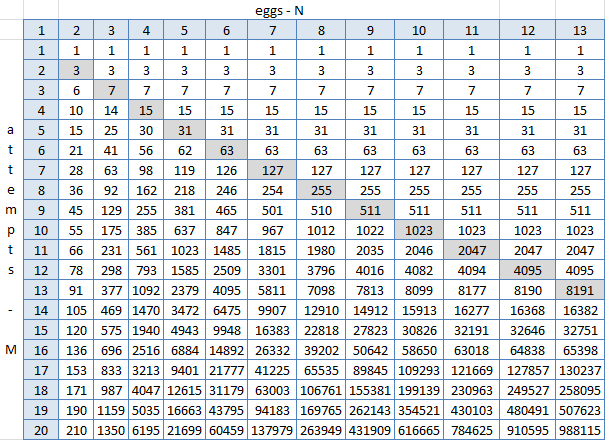
Diagonal abu-abu adalah N = M, dan di sini terlihat jelas bahwa di sebelah kanannya (untuk N> M) tidak ada yang berubah. Itu bisa dilihat - tetapi tidak bisa sebaliknya, karena ini semua adalah hasil kerja formula, di mana diberikan bahwa setiap sel sama dengan jumlah atas, kiri atas dan satu. Tetapi beberapa formula universal di mana Anda dapat mengganti N dan M dan mendapatkan nomor lantai tidak ditemukan. Spoiler: tidak ada. Tetapi kemudian sangat mudah untuk membuat tabel ini di Excel, mungkinkah menghasilkan python yang sama dan menarik jawaban darinya?
Numpy kamu tidak
Saya ingat bahwa ada NumPy, yang hanya dirancang untuk bekerja dengan array multidimensi, mengapa tidak mencobanya? Untuk memulainya, kita membutuhkan array satu dimensi dari nol ukuran N + 1 Dan array satu dimensi dari unit ukuran N. Ambil array pertama dari nol ke elemen kedua dari belakang, tambahkan elemen dengan array pertama dari elemen pertama ke yang terakhir dan dengan array unit. Ke array yang dihasilkan, tambahkan nol ke awal. Ulangi M kali. Elemen nomor N dari array yang dihasilkan akan menjadi jawabannya. 3 langkah pertama terlihat seperti ini:
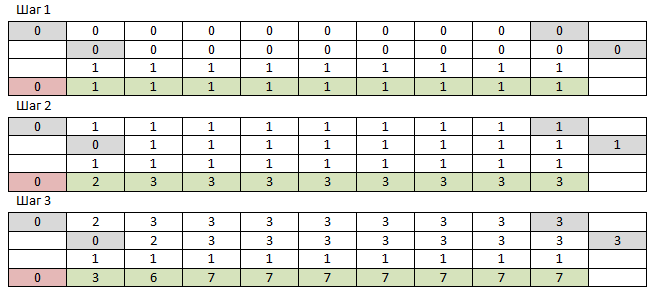
NumPy bekerja sangat cepat sehingga saya tidak menyimpan seluruh tabel - setiap kali saya membaca baris yang diperlukan lagi. Satu hal - hasil bekerja pada angka besar salah. Pangkat yang lebih tinggi seperti mereka, sedangkan yang lebih rendah tidak. Ini adalah bagaimana kesalahan aritmatika angka floating-point terakumulasi dari beberapa penambahan terlihat seperti. Tidak masalah - Anda dapat mengubah jenis array menjadi int. Tidak, masalah - ternyata demi kecepatan NumPy hanya bekerja dengan tipe datanya, dan intnya, tidak seperti int Python, tidak boleh lebih dari 2 ^ 64-1, setelah itu diam-diam meluap dan berlanjut dengan -2 ^ 64. Dan saya benar-benar mengharapkan angka di bawah tiga ribu karakter. Tetapi bekerja sangat cepat, f (9477, 10000) berjalan 233 ms, itu hanya menghasilkan semacam omong kosong pada output. Saya bahkan tidak akan memberikan kode, karena hal seperti itu. Saya akan mencoba membuat python yang sama bersih.
Iterasi, iterasi, tapi tidak iterasi
def height(n, m): arr = [0]*(n+1) while m > 0: arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) m-=1 return arr[n]
44 detik untuk menghitung f (9477, 10000) sedikit banyak. Tapi tentu saja pasti. Apa yang bisa dioptimalkan? Pertama, tidak perlu mempertimbangkan segalanya di sebelah kanan M diagonal, M. Yang kedua - untuk mempertimbangkan array terakhir secara keseluruhan, demi satu sel. Untuk ini, dua dua sel terakhir dari yang sebelumnya akan cocok. Untuk menghitung f (10, 20), hanya sel abu-abu ini yang cukup:
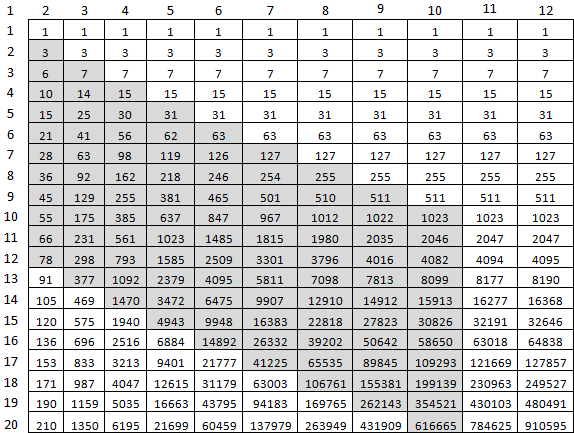
Dan itu terlihat dalam kode:
def height(n, m): arr = [0, 1, 1] i = 1 while i < n and i < mn:
Dan apa yang Anda pikirkan? f (9477, 10000) dalam 2 detik! Tetapi input ini terlalu bagus, panjang array pada setiap tahap tidak akan lebih dari 533 elemen (10000-9477). Mari kita periksa f (5477, 10000) - 11 detik. Ini juga bagus, tetapi hanya dibandingkan dengan 44 detik - dua puluh tes dengan waktu ini tidak akan berlalu.
Bukan itu. Tetapi karena ada tugas, maka ada solusi, pencarian berlanjut. Saya mulai melihat tabel Excel lagi. Sel di sebelah kiri (m, m) selalu kurang satu. Dan sel di sebelah kiri itu tidak ada lagi, di setiap baris perbedaannya menjadi lebih besar. Sel di bawah ini (m, m) selalu dua kali lebih besar. Dan sel di bawahnya tidak lagi dua kali, tetapi sedikit lebih kecil, tetapi untuk setiap kolom berbeda, semakin jauh, semakin besar. Dan juga angka-angka dalam satu baris pada awalnya tumbuh dengan cepat, dan setelah tengah perlahan. Biarkan saya membuat tabel perbedaan antara sel-sel tetangga, mungkin pola apa yang akan muncul di sana?
Lebih hangat
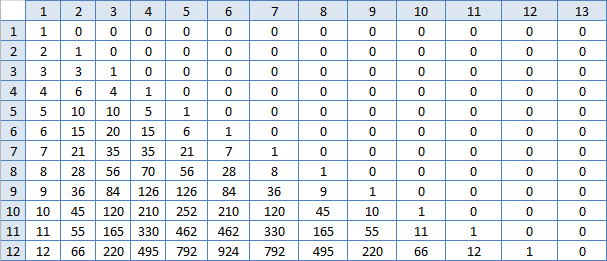
Bah, nomor yang sudah Anda kenal! Yaitu, jumlah N dari angka-angka ini dalam jumlah baris M apakah ini jawabannya? Benar, menghitung mereka hampir sama dengan apa yang sudah saya lakukan, tidak mungkin ini akan sangat mempercepat pekerjaan. Tetapi Anda harus mencoba:
f (9477, 10000): 17 detik def height(n, m): arr = [1,1] while m > 1: arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) + [1] m-=1 return sum(arr[1:n+1])
Atau 8, jika Anda hanya menghitung setengah segitiga def height(n, m): arr = [1,1] while m > 2 and len(arr) < n+2:
Belum lagi solusi yang lebih optimal. Ini bekerja lebih cepat pada beberapa data, lebih lambat pada beberapa. Kita harus masuk lebih dalam. Apa segitiga ini dengan angka yang muncul dalam solusi dua kali? Sangat memalukan untuk mengakuinya, tetapi saya telah dengan aman melupakan matematika yang lebih tinggi, di mana segitiga itu pasti ada, jadi saya harus mencarinya di google.
Bingo!
Segitiga Pascal , seperti yang secara resmi disebut. Tabel koefisien binomial tak terbatas. Jadi jawaban untuk masalah dengan N telur dan lemparan M adalah jumlah dari koefisien N pertama dalam perluasan binomial Newton dari derajat Mth, kecuali untuk nol.
Koefisien binomial sewenang-wenang dapat dihitung melalui faktorial dari nomor baris dan jumlah koefisien di baris: bk = m! / (N! * (Mn!)). Tetapi bagian terbaiknya adalah Anda dapat menghitung secara berurutan angka-angka dalam string, mengetahui angka dan koefisien nol (selalu satu): bk [n] = bk [n-1] * (m - n + 1) / n. Pada setiap langkah, pembilang berkurang satu, dan penyebut meningkat. Dan solusi akhir yang ringkas terlihat seperti ini:
def height(n, m): h, bk = 0, 1
33 md untuk perhitungan f (9477, 10000)! Solusi ini juga dapat dioptimalkan, meskipun dalam rentang yang diberikan dan berfungsi dengan baik. Jika n terletak di bagian kedua dari segitiga, maka kita dapat membalikkannya ke mn, menghitung jumlah koefisien n pertama dan kurangi dari 2 ^ m-2. Jika n dekat dengan tengah dan m adalah ganjil, maka perhitungannya juga dapat dikurangi: jumlah paruh pertama baris akan menjadi 2 ^ (m-1) -1, koefisien terakhir di babak pertama dapat dihitung melalui faktorial, jumlahnya adalah (m-1) / 2, dan kemudian terus tambahkan koefisien jika n ada di bagian kanan segitiga, atau kurangi jika di sebelah kiri. Jika m adalah genap, maka Anda tidak dapat menghitung setengah dari garis, tetapi Anda dapat menemukan jumlah dari koefisien m / 2 + 1 pertama dengan menghitung rata-rata melalui faktorial dan menambahkan setengahnya ke 2 ^ (m-1) -1. Pada input data di wilayah 10 ^ 6, ini sangat mengurangi waktu eksekusi.
Setelah keputusan yang berhasil, saya mulai mencari penelitian orang lain tentang masalah ini, tetapi saya hanya menemukan hal yang sama, dari wawancara, dengan hanya dua telur, dan ini bukan olahraga. Internet akan menjadi tidak lengkap tanpa keputusan saya, saya memutuskan, dan ini dia.