Pemrograman Dinamis atau Divide and Conquer

Artikel ini membahas persamaan dan perbedaan antara dua pendekatan untuk menyelesaikan masalah algoritmik: pemrograman dinamis (pemrograman dinamis) dan prinsip "divide and conquer" (divide and conquer). Kami akan membandingkan menggunakan dua algoritma sebagai contoh: pencarian biner (cara cepat menemukan angka dalam array yang diurutkan) dan jarak Levenshtein (cara mengkonversi satu baris ke yang lain dengan jumlah operasi minimum).

Saya ingin segera mencatat bahwa perbandingan dan penjelasan ini tidak mengklaim sangat benar. Dan mungkin bahkan beberapa profesor universitas ingin mengeluarkan saya :) Artikel ini hanyalah upaya pribadi saya untuk menyelesaikan masalah dan memahami apa pemrograman dinamis dan bagaimana prinsip "membagi dan menaklukkan" dilibatkan.

Jadi, mari kita mulai ...

Masalah

Ketika saya mulai mempelajari algoritma, sulit bagi saya untuk memahami ide dasar pemrograman dinamis (selanjutnya DP , dari Pemrograman Dinamis) dan bagaimana ia berbeda dari pendekatan "divide and conquer" (selanjutnya DC , dari divide-and-conquer). Ketika datang untuk membandingkan kedua paradigma ini, biasanya banyak yang berhasil menggunakan fungsi Fibonacci untuk menggambarkan. Dan ini adalah ilustrasi yang bagus. Tetapi bagi saya tampaknya ketika kita menggunakan tugas yang sama untuk menggambarkan DP dan DC, kita kehilangan satu detail penting yang dapat membantu kita menangkap perbedaan antara dua pendekatan lebih cepat. Dan detail ini adalah bahwa kedua teknik ini paling dimanifestasikan dalam menyelesaikan berbagai jenis masalah.

Saya masih dalam proses belajar DP dan DC dan saya tidak bisa mengatakan bahwa saya sepenuhnya memahami konsep-konsep ini. Tetapi saya masih berharap bahwa artikel ini akan memberi tambahan cahaya dan membantu mengambil langkah selanjutnya dalam mempelajari pendekatan signifikan seperti pemrograman dinamis dan divide-and-conquer.

Kesamaan antara DP dan DC

Cara saya melihat kedua konsep ini sekarang, saya dapat menyimpulkan bahwa DP adalah versi tambahan dari DC .

Saya tidak akan menganggap mereka sesuatu yang sama sekali berbeda. Karena kedua konsep ini secara rekursif membagi masalah menjadi dua atau lebih subproblem dari jenis yang sama sampai subproblem ini cukup mudah untuk diselesaikan secara langsung. Selanjutnya, semua solusi untuk subproblem digabungkan bersama untuk akhirnya memberikan jawaban atas masalah asli.

Jadi, mengapa kita masih memiliki dua pendekatan berbeda (DP dan DC) dan mengapa saya menyebut pemrograman dinamis sebagai ekstensi. Ini karena pemrograman dinamis dapat diterapkan pada tugas yang memiliki karakteristik dan batasan tertentu. Dan hanya dalam hal ini DP memperluas DC melalui dua teknik: memoisasi dan tabulasi .

Mari kita sedikit lebih dalam ke detail ...

Keterbatasan dan karakteristik yang diperlukan untuk pemrograman dinamis

Seperti yang baru saja kita ketahui, ada dua karakteristik utama yang harus dimiliki oleh suatu tugas / masalah agar kita dapat menyelesaikannya menggunakan pemrograman dinamis:

1. Substruktur optimal - harus mungkin untuk menyusun solusi optimal untuk masalah dari solusi optimal ke subtugasnya.
2. Persimpangan subproblem - masalahnya harus dipecah menjadi subproblem, yang pada gilirannya digunakan kembali berulang kali. Dengan kata lain, pendekatan rekursif untuk memecahkan masalah akan menyiratkan solusi berganda ( bukan tunggal) untuk subproblem yang sama, alih-alih menghasilkan subproblem baru dan unik di setiap siklus rekursif.

Segera setelah kami dapat menemukan dua karakteristik ini dalam masalah yang kami pertimbangkan, kami dapat mengatakan bahwa itu dapat diselesaikan menggunakan pemrograman dinamis.

Pemrograman dinamis sebagai perpanjangan dari prinsip "divide and conquer"

DP memperluas DC dengan bantuan dua teknik ( memoisasi dan tabulasi ), yang tujuannya adalah untuk menyimpan solusi untuk submasalah untuk digunakan kembali di masa depan. Dengan demikian, solusi di-cache oleh subproblem, yang mengarah ke peningkatan yang signifikan dalam kinerja algoritma. Sebagai contoh, kompleksitas waktu dari implementasi rekursif "naif" dari fungsi Fibonacci adalah O(2 n ) . Pada saat yang sama, solusi berdasarkan pemrograman dinamis dieksekusi hanya dalam waktu (n) .

Memoisasi (mengisi cache dari atas ke bawah) adalah teknik caching yang menggunakan solusi yang baru dihitung untuk subtugas. Fungsi Fibonacci menggunakan teknik memoisasi akan terlihat seperti ini:

 memFib(n) { if (mem[n] is undefined) if (n < 2) result = n else result = memFib(n-2) + memFib(n-1) mem[n] = result return mem[n] } 

Tabulasi (mengisi cache dari bawah ke atas) adalah teknik yang serupa, tetapi yang terutama difokuskan pada pengisian cache, dan bukan pada menemukan solusi untuk subproblem. Perhitungan nilai-nilai yang perlu di-cache paling mudah dalam hal ini dilakukan secara iteratif, daripada secara rekursif. Fungsi Fibonacci menggunakan teknik tabulasi akan terlihat seperti ini:

 tabFib(n) { mem[0] = 0 mem[1] = 1 for i = 2...n mem[i] = mem[i-2] + mem[i-1] return mem[n] } 

Anda dapat membaca lebih lanjut tentang perbandingan memoisasi dan tabulasi di sini .

Gagasan utama yang perlu ditangkap dalam contoh-contoh ini adalah bahwa karena masalah DC kami memiliki subproblem yang tumpang tindih, kami dapat menggunakan caching solusi untuk subproblem menggunakan salah satu dari dua teknik caching: memoisasi dan tabulasi.

Jadi apa perbedaan antara DP dan DC pada akhirnya

Kami belajar tentang batasan dan prasyarat untuk menggunakan pemrograman dinamis, serta teknik caching yang digunakan dalam pendekatan DP. Mari kita rangkum dan gambarkan pemikiran di atas dalam ilustrasi berikut:



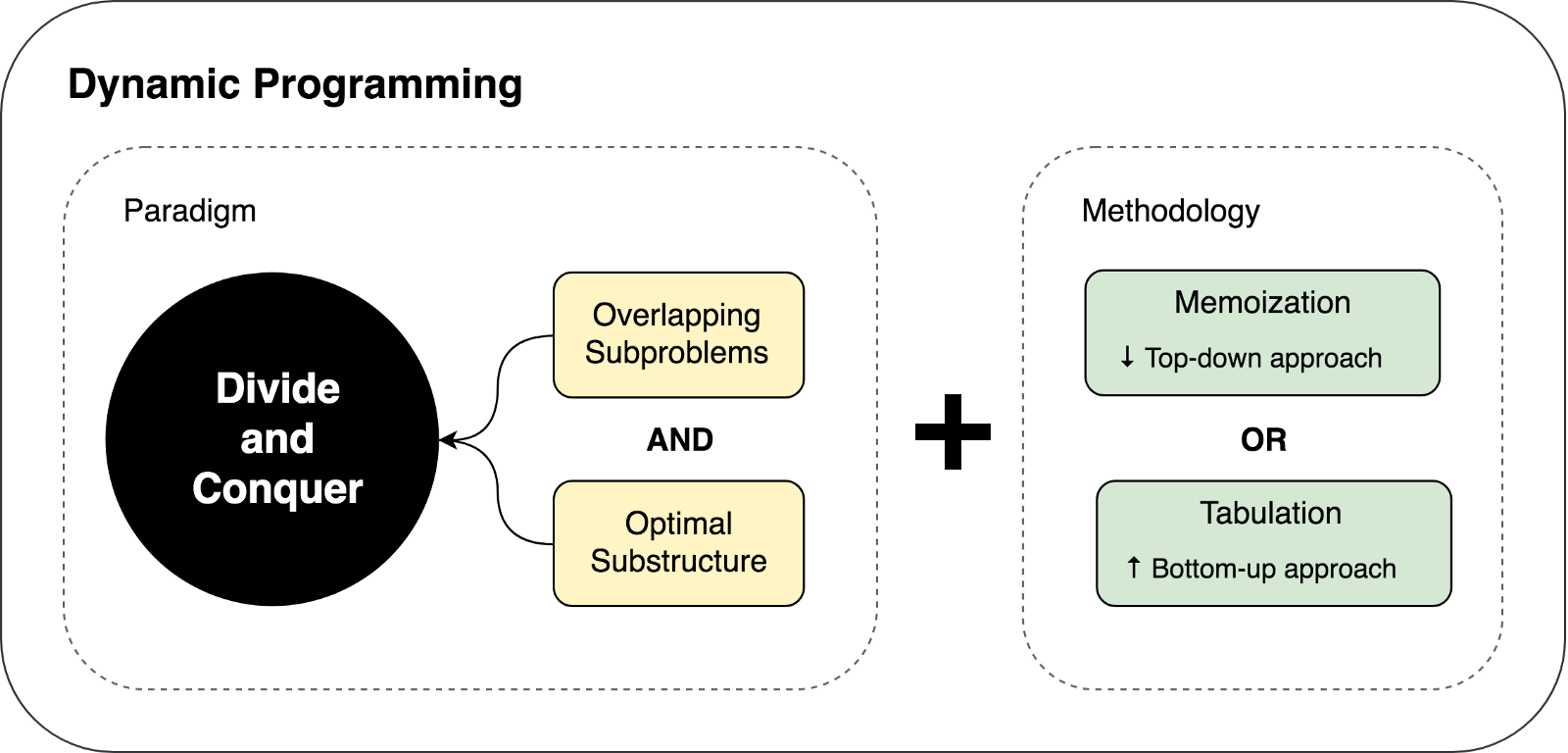
Mari kita coba memecahkan beberapa masalah menggunakan DP dan DC untuk menunjukkan kedua pendekatan ini dalam tindakan.

Divide and Conquer Contoh: Pencarian Biner

Algoritma pencarian biner adalah algoritma pencarian yang menemukan posisi elemen yang diminta dalam array yang diurutkan. Dalam pencarian biner, kami membandingkan nilai variabel dengan nilai elemen di tengah array. Jika mereka tidak sama, maka setengah dari array di mana elemen yang diinginkan tidak dapat dikecualikan dari pencarian lebih lanjut. Pencarian berlanjut di setengah dari array, di mana variabel yang diinginkan dapat ditemukan sampai ditemukan. Jika setengah dari array tidak mengandung elemen, pencarian dianggap selesai dan kami menyimpulkan bahwa array tidak mengandung nilai yang diinginkan.

Contoh

Ilustrasi di bawah ini adalah contoh pencarian biner untuk angka 4 dalam array.



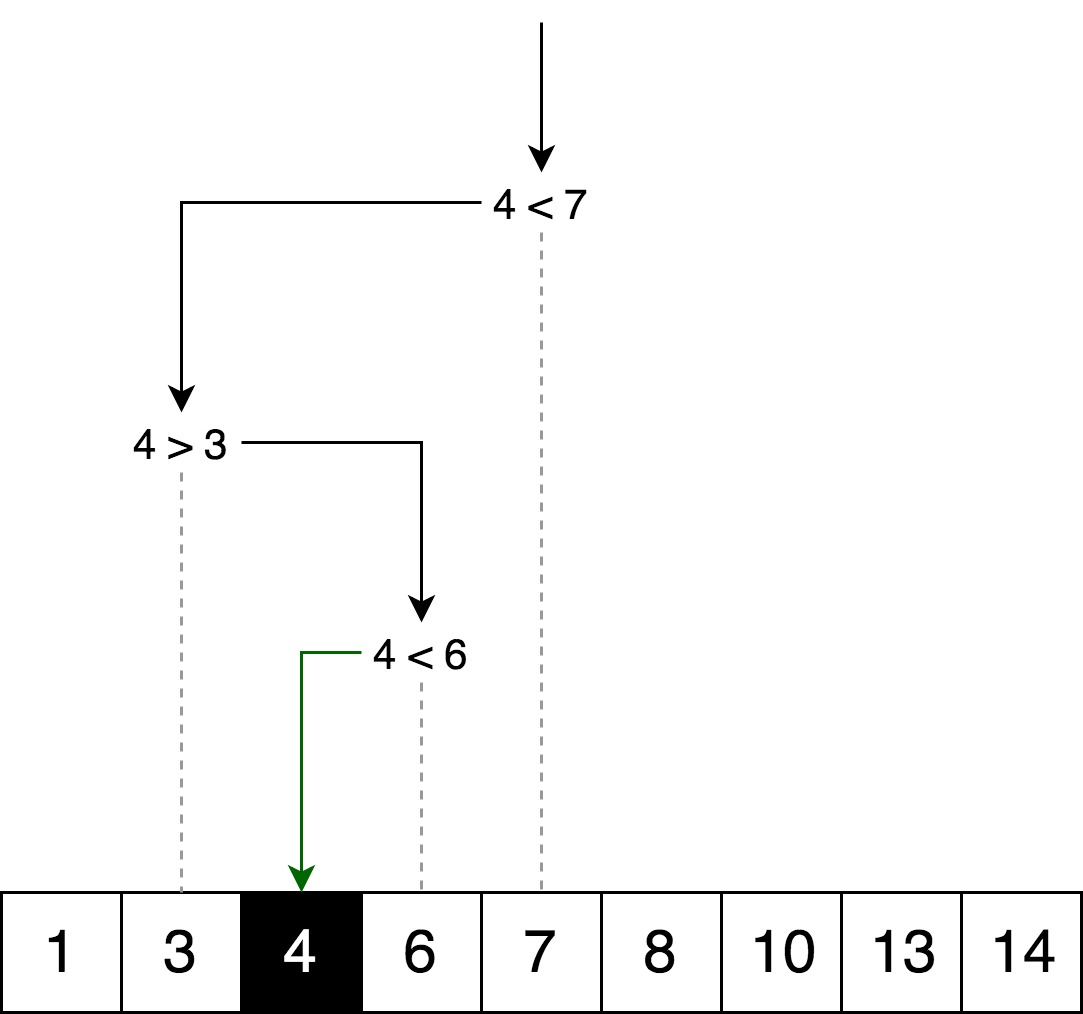
Mari kita gambarkan logika pencarian yang sama, tetapi dalam bentuk "pohon keputusan".



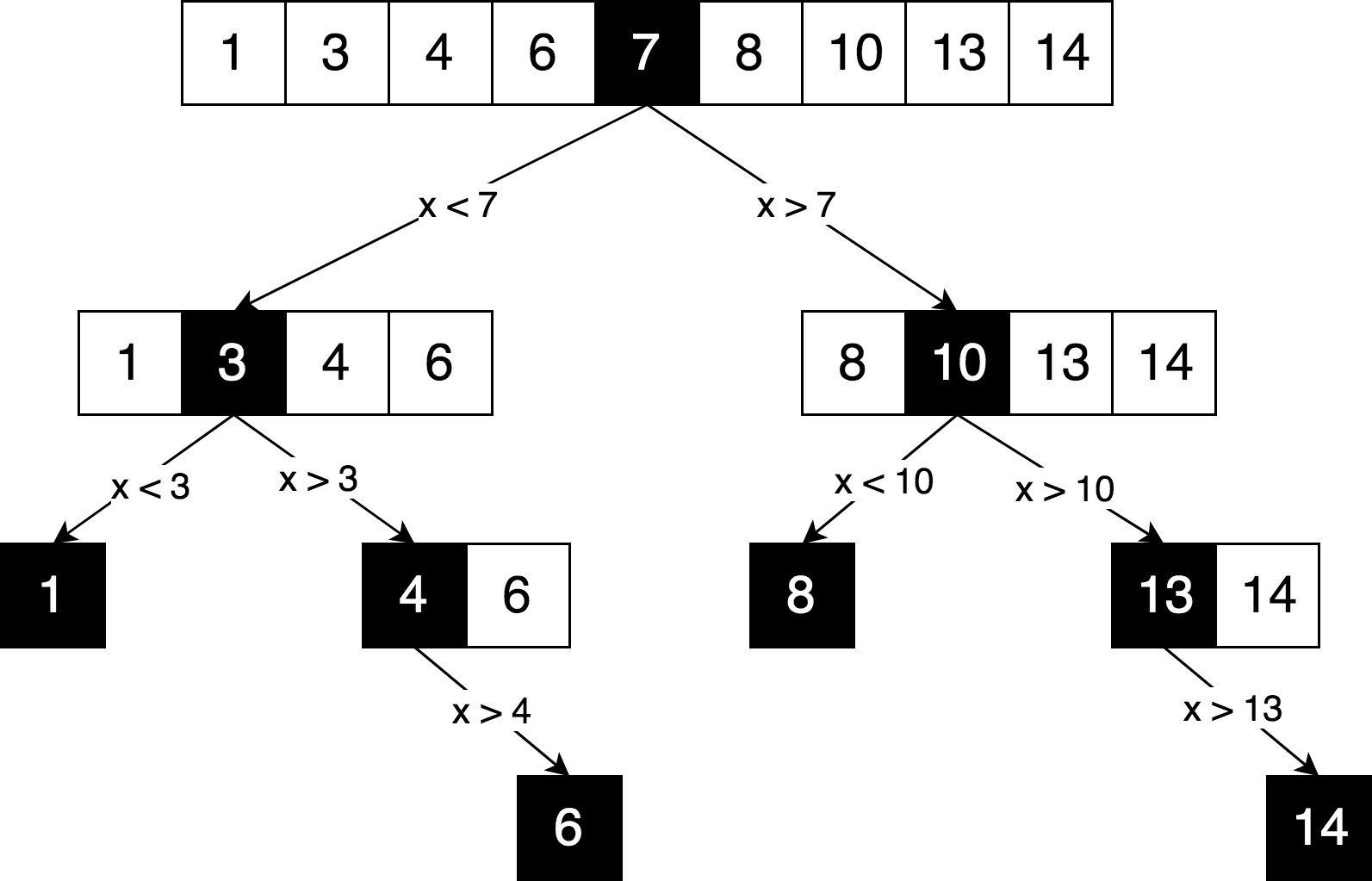
Anda dapat melihat dalam diagram ini prinsip yang jelas tentang "bagilah dan taklukkan", yang digunakan untuk menyelesaikan masalah ini. Kami secara iteratif membagi array asli kami menjadi sub-sus dan mencoba menemukan elemen yang kami cari sudah ada di dalamnya.

Bisakah kita mengatasi masalah ini menggunakan pemrograman dinamis? Tidak. Karena tugas ini tidak mengandung subproblem berpotongan . Setiap kali kami membagi array menjadi beberapa bagian, kedua bagian tersebut sepenuhnya independen dan tidak tumpang tindih. Dan sesuai dengan asumsi dan batasan pemrograman dinamis yang kita bahas di atas, subproblem entah bagaimana harus tumpang tindih, mereka harus berulang .

Biasanya, setiap kali pohon keputusan terlihat persis seperti pohon (dan tidak seperti grafik ), ini kemungkinan besar berarti tidak ada subproblem yang tumpang tindih,

Implementasi algoritma

Di sini Anda dapat menemukan kode sumber lengkap dari algoritma pencarian biner dengan tes dan penjelasan.

 function binarySearch(sortedArray, seekElement) { let startIndex = 0; let endIndex = sortedArray.length - 1; while (startIndex <= endIndex) { const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2); // If we've found the element just return its position. if (sortedArray[middleIndex] === seekElement)) { return middleIndex; } // Decide which half to choose: left or right one. if (sortedArray[middleIndex] < seekElement)) { // Go to the right half of the array. startIndex = middleIndex + 1; } else { // Go to the left half of the array. endIndex = middleIndex - 1; } } return -1; } 

Contoh Pemrograman Dinamis: Mengedit Jarak

Biasanya, ketika datang untuk menjelaskan pemrograman dinamis, fungsi Fibonacci digunakan sebagai contoh. Tetapi dalam kasus kami, mari kita ambil contoh yang sedikit lebih kompleks. Semakin banyak contoh, semakin mudah untuk memahami konsep.

Jarak pengeditan (atau jarak Levenshtein) antara dua baris adalah jumlah operasi minimum untuk menyisipkan satu karakter, menghapus satu karakter dan mengganti satu karakter dengan yang lain, yang diperlukan untuk mengubah satu baris menjadi yang lain.

Contoh

Misalnya, jarak pengeditan antara kata "kitten" dan "sitting" adalah 3, karena Anda perlu melakukan tiga operasi pengeditan (dua penggantian dan satu sisipan) untuk mengonversi satu baris ke yang lain. Dan tidak mungkin menemukan opsi konversi yang lebih cepat dengan operasi yang lebih sedikit:

1. kitten → sitten (mengganti "k" dengan "s")
2. sitten → sittin (mengganti “e” dengan “i”)
3. duduk → duduk (masukkan "g" sepenuhnya).

Aplikasi algoritma

Algoritme ini memiliki beragam aplikasi, misalnya untuk pemeriksaan ejaan, sistem koreksi pengenalan optik, pencarian string yang tidak akurat, dll.

Definisi matematika dari suatu masalah

Secara matematis, jarak Levenstein antara dua garis a, b (dengan panjang | a | dan |b| masing-masing) ditentukan oleh fungsi function lev(|a|, |b|) , di mana:



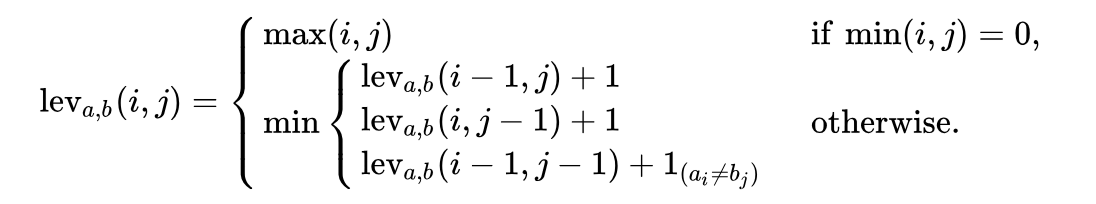
Harap dicatat bahwa baris pertama dalam fungsi min sesuai dengan operasi hapus , baris kedua sesuai dengan operasi sisipan dan baris ketiga sesuai dengan operasi penggantian (jika huruf-hurufnya tidak sama).

Penjelasan

Mari kita coba mencari tahu apa yang dikatakan formula ini kepada kita. Ambil contoh sederhana untuk menemukan jarak pengeditan minimum antara ME dan baris MY . Secara intuitif, Anda sudah tahu bahwa jarak pengeditan minimum adalah satu ( 1 ) operasi penggantian (ganti "E" dengan "Y"). Tetapi mari kita meresmikan solusi kita dan mengubahnya menjadi bentuk algoritmik, agar dapat menyelesaikan versi yang lebih kompleks dari masalah ini, seperti mengubah kata Saturday menjadi Sunday .

Untuk menerapkan rumus pada transformasi ME → MY, pertama-tama kita harus mengetahui jarak pengeditan minimum antara ME → M, M → MY dan M → M. Selanjutnya, kita harus memilih minimal tiga jarak dan menambahkan padanya satu operasi (+1) dari transformasi E → Y.

Jadi, kita sudah dapat melihat sifat rekursif dari solusi ini: jarak pengeditan minimum ME → MY dihitung berdasarkan tiga kemungkinan transformasi sebelumnya. Jadi, kita sudah dapat mengatakan bahwa ini adalah algoritma divide and conquer.

Untuk lebih menjelaskan algoritma, mari kita letakkan dua baris kita dalam sebuah matriks:



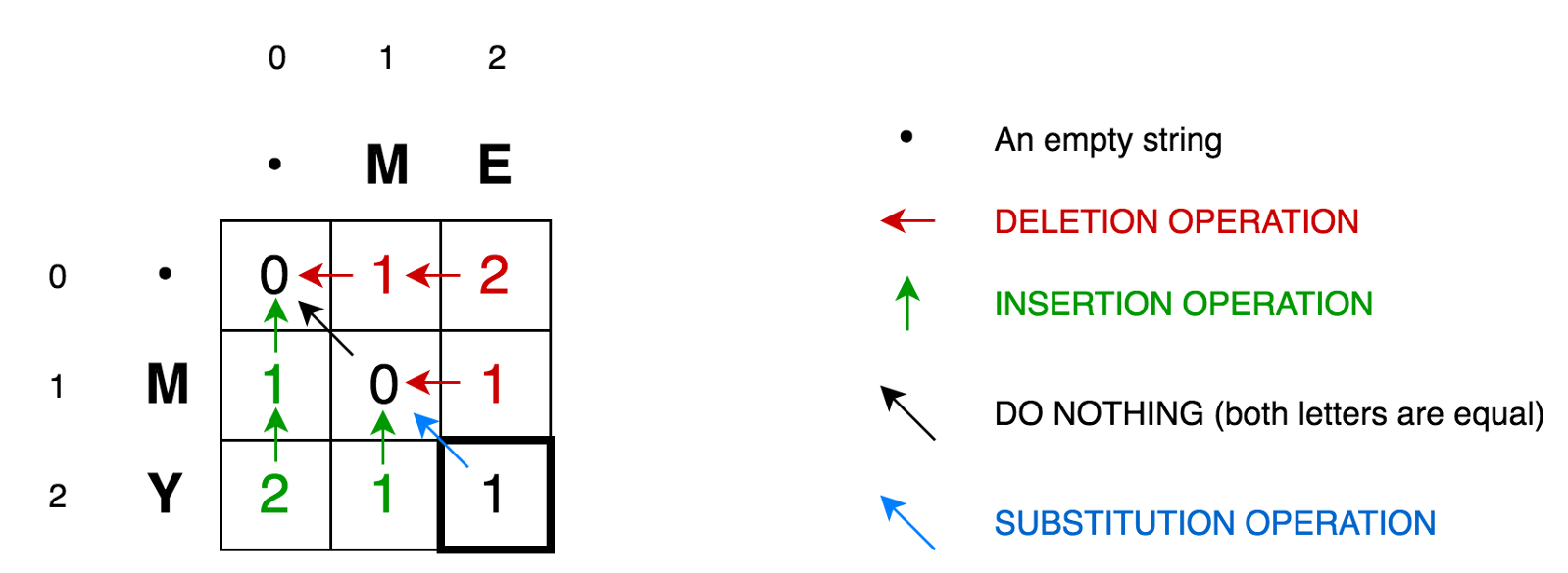Sel (0,1) berisi angka merah 1. Ini berarti bahwa kita perlu melakukan 1 operasi untuk mengubah M menjadi string kosong - hapus M. Oleh karena itu, kami telah menandai angka ini dengan warna merah.

Sel (0,2) berisi angka merah 2. Ini berarti bahwa kita perlu melakukan 2 operasi untuk mengubah string ME menjadi string kosong - hapus E, hapus M.

Sel (1,0) berisi angka hijau 1. Ini berarti bahwa kita memerlukan 1 operasi untuk mengubah string kosong menjadi M - tempel M. Kami menandai operasi sisipan berwarna hijau.

Sel (2,0) berisi angka hijau 2. Ini berarti bahwa kita perlu melakukan 2 operasi untuk mengubah string kosong menjadi string MY - masukkan Y, masukkan M.

Sel (1,1) berisi angka 0. Ini berarti bahwa kita tidak perlu melakukan operasi apa pun untuk mengubah string M menjadi M.

Sel (1,2) berisi angka merah 1. Ini berarti bahwa kita perlu melakukan 1 operasi untuk mengubah string ME menjadi M - hapus E.

Dan seterusnya ...

Itu tidak terlihat sulit untuk matriks kecil, seperti kita (hanya 3x3). Tetapi bagaimana kita bisa menghitung nilai semua sel untuk matriks besar (misalnya, untuk matriks 9x7 dalam transformasi Sabtu → Minggu)?

Berita baiknya adalah, sesuai dengan rumus, yang kita butuhkan untuk menghitung nilai sel apa pun dengan koordinat (i,j) hanyalah nilai dari 3 sel tetangga (i-1,j) , (i-1,j-1) , dan (i,j-1) . Yang perlu kita lakukan adalah menemukan nilai minimum tiga sel tetangga dan menambahkan satu (+1) ke nilai ini jika kita memiliki huruf yang berbeda di baris ke-i dan kolom ke-j.

Jadi sekali lagi, Anda dapat dengan jelas melihat sifat rekursif dari tugas ini.



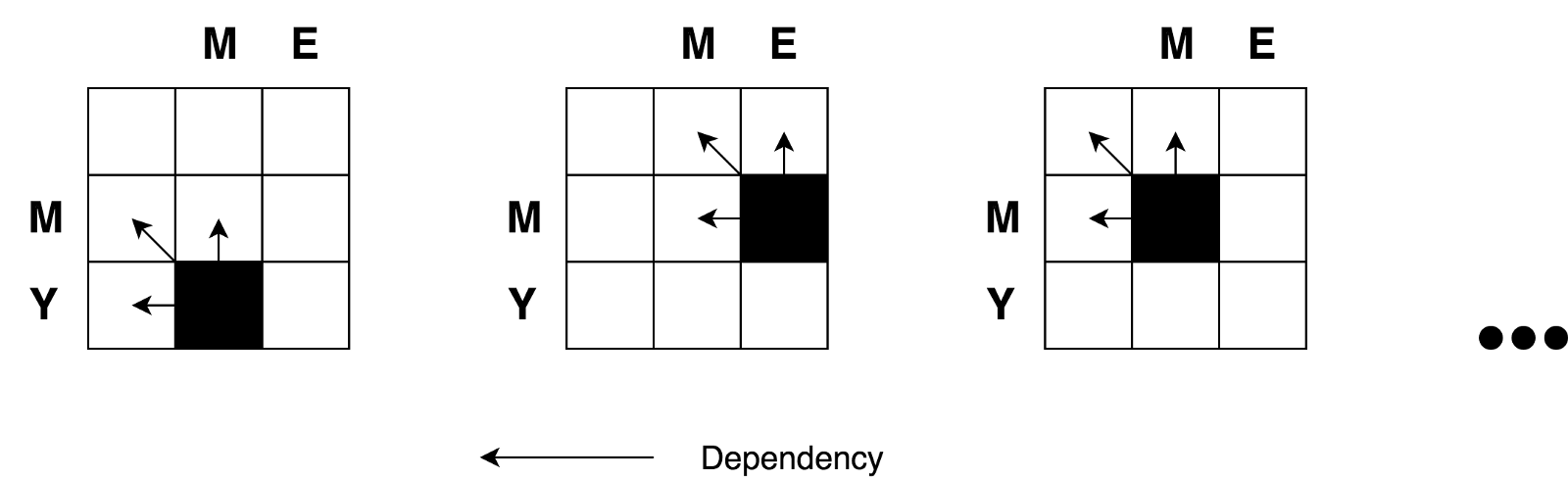
Kami juga melihat bahwa kami berhadapan dengan tugas membagi dan menaklukkan. Tetapi, dapatkah kita menerapkan pemrograman dinamis untuk mengatasi masalah ini? Apakah tugas ini memenuhi persyaratan " masalah berpotongan " dan " substruktur optimal " yang disebutkan di atas? Ya Mari kita membangun pohon keputusan.



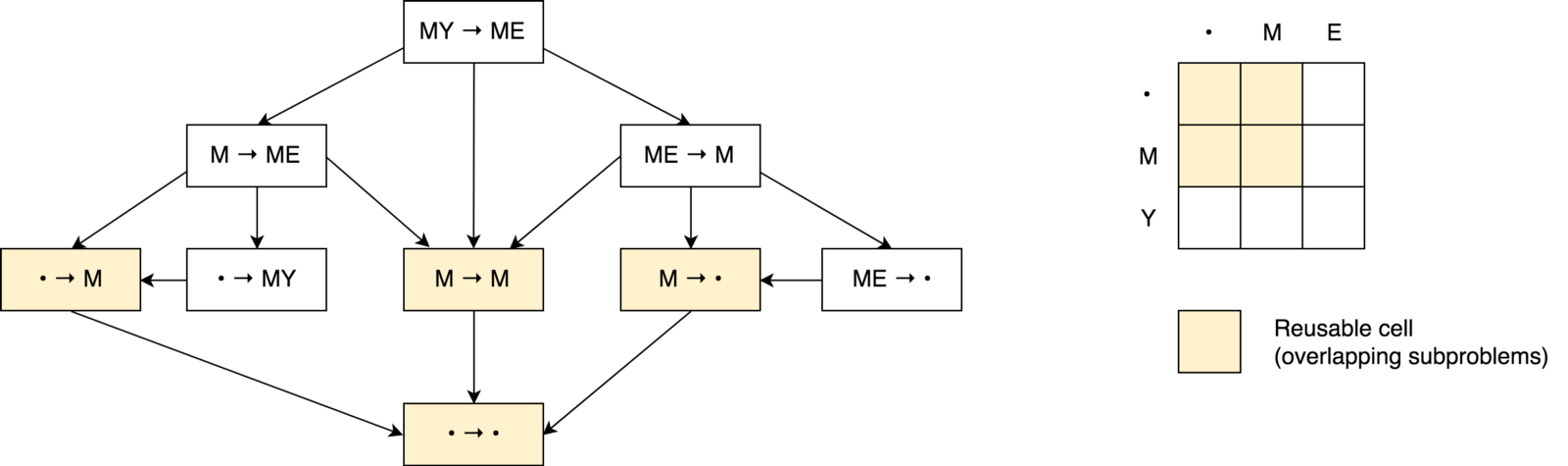
Pertama, Anda mungkin memperhatikan bahwa pohon keputusan kami lebih mirip grafik keputusan daripada pohon . Anda juga dapat melihat beberapa subtugas yang tumpang tindih . Terlihat juga bahwa tidak mungkin untuk mengurangi jumlah operasi dan membuatnya lebih kecil dari jumlah operasi dari ketiga sel tetangga (sub-masalah).

Anda juga dapat memperhatikan bahwa nilai di setiap sel dihitung berdasarkan nilai sebelumnya. Jadi, dalam hal ini, teknik tabulasi digunakan (mengisi cache dalam arah bottom-up). Anda akan melihat ini dalam contoh kode di bawah ini.

Dengan menerapkan semua prinsip ini, kita dapat memecahkan masalah yang lebih kompleks, misalnya, tugas transformasi Sabtu → Minggu:



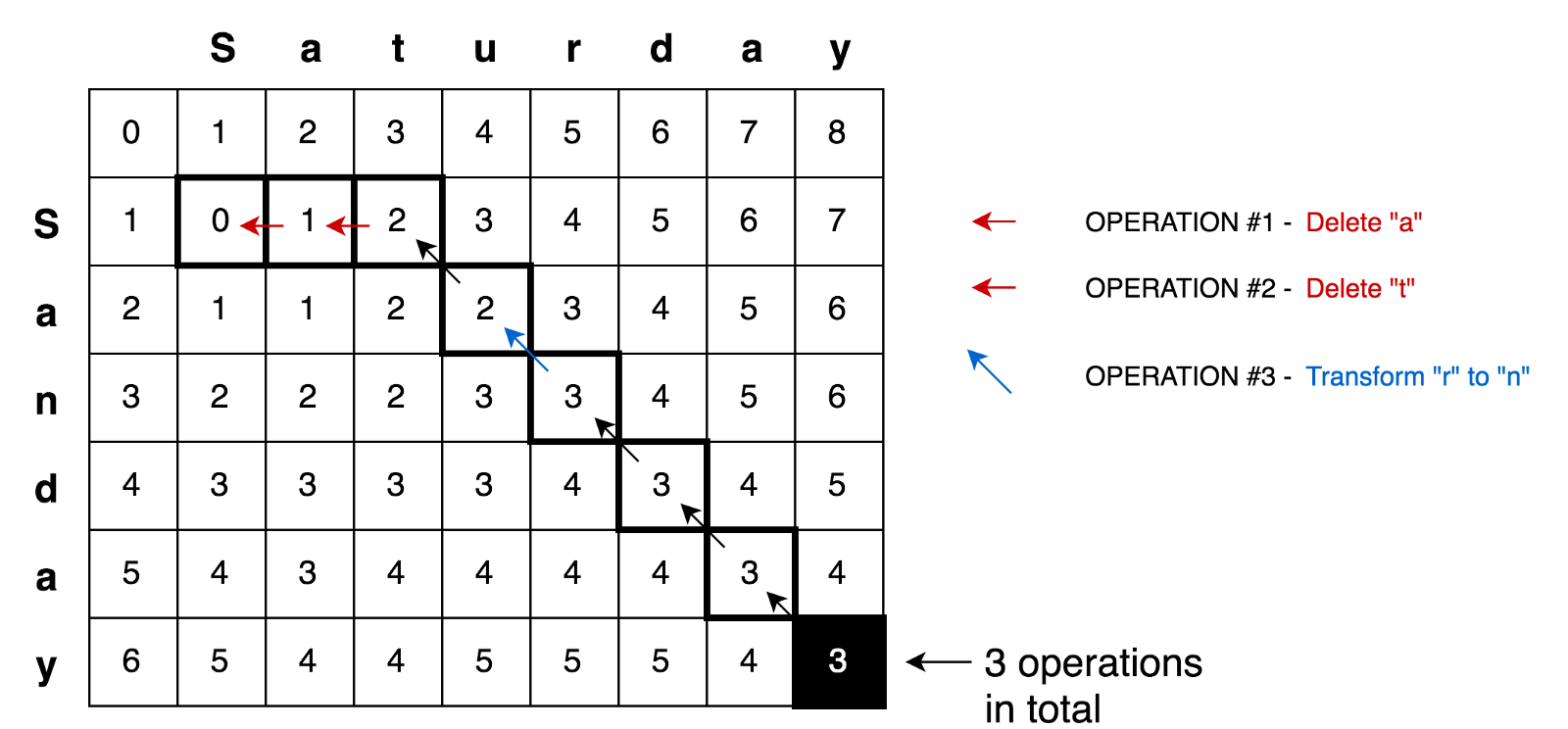Contoh kode

Di sini Anda dapat menemukan solusi lengkap untuk menemukan jarak pengeditan minimum dengan tes dan penjelasan:

 function levenshteinDistance(a, b) { const distanceMatrix = Array(b.length + 1) .fill(null) .map( () => Array(a.length + 1).fill(null) ); for (let i = 0; i <= a.length; i += 1) { distanceMatrix[0][i] = i; } for (let j = 0; j <= b.length; j += 1) { distanceMatrix[j][0] = j; } for (let j = 1; j <= b.length; j += 1) { for (let i = 1; i <= a.length; i += 1) { const indicator = a[i - 1] === b[j - 1] ? 0 : 1; distanceMatrix[j][i] = Math.min( distanceMatrix[j][i - 1] + 1, // deletion distanceMatrix[j - 1][i] + 1, // insertion distanceMatrix[j - 1][i - 1] + indicator, // substitution ); } } return distanceMatrix[b.length][a.length]; } 

Kesimpulan

Dalam artikel ini, kami membandingkan dua pendekatan algoritmik ("pemrograman dinamis" dan "membagi dan menaklukkan") untuk memecahkan masalah. Kami menemukan bahwa pemrograman dinamis menggunakan prinsip "divide and conquer" dan dapat diterapkan untuk menyelesaikan masalah jika masalah tersebut mengandung subproblem berpotongan dan substruktur optimal (seperti halnya dengan jarak Levenshtein). Pemrograman dinamis lebih lanjut menggunakan teknik memoisasi dan tabulasi untuk mempertahankan sub-resolusi untuk digunakan kembali nanti.

Saya harap artikel ini mengklarifikasi daripada mempersulit situasi bagi Anda yang mencoba untuk berurusan dengan konsep-konsep penting seperti pemrograman dinamis dan "membagi dan menaklukkan" :)

Anda dapat menemukan lebih banyak contoh algoritmik menggunakan pemrograman dinamis, dengan tes dan penjelasan dalam repositori Algoritma JavaScript dan Struktur Data .

Pengodean yang berhasil!