“Mudah saja. Kami mengambil metrik Schwarzschild, mencari simbol Christoffel, menghitung turunannya, menulis persamaan geodesik, mengubah beberapa koordinat Cartesian (agar tidak menderita), mendapatkan ODE multi-garis besar - dan menyelesaikannya. Sesuatu seperti itu. "



Sekarang jelas bahwa lubang hitam itu menyedot saya. Mereka menarik tanpa henti. Terakhir kali saya menemukan cara memvisualisasikan geometri Schwarzschild. Saya tertelan oleh masalah representasi akurat tentang bagaimana kelengkungan ruang-waktu seperti itu mempengaruhi penampilan langit (karena foton dari sumber yang jauh bergerak di sepanjang garis geodesi yang melengkung oleh lubang hitam) untuk membuat simulasi interaktif. Inilah hasilnya (berfungsi di browser). Caranya adalah dengan memaksimalkan perhitungan penyimpangan sinar cahaya. Semuanya berfungsi lebih atau kurang normal, tetapi tentu saja, simulasi semacam itu jauh dari ideal, karena pada kenyataannya tidak ada pelacakan dilakukan di sana (untuk non-spesialis: pemulihan lokasi sinar cahaya jatuh ke kamera kembali ke masa lalu).

Proyek baru saya memperbaiki kekurangan ini dengan meninggalkan efisiensi / interaktivitas dengan cara yang paling sederhana: ini adalah pelacak sinar murni pada CPU . Penelusuran dilakukan seakurat dan selama mungkin. Merender gambar di atas membutuhkan waktu 15 5 menit (terima kasih, RK4) di laptop saya.

Tidak ada peningkatan dibandingkan dengan karya serupa. Saya sangat menikmati melakukannya. Saya menulis artikel ini untuk membagikan tidak hanya hasilnya, seperti gambar di atas ( terutama karena orang lain melakukan lebih baik ), tetapi juga proses membuat gambar-gambar ini , dengan diskusi / penjelasan fisika dan implementasi. Idealnya, ini dapat menginspirasi atau menjadi panduan bagi orang-orang dengan minat yang sama.

Cari rendering baru dengan tag tanpa bintang di tumlr.

Sedikit optik pseudo-Riemann

Bayangan

Jika Anda sudah mencoba applet saya, maka Anda sudah familiar dengan gambar ini:



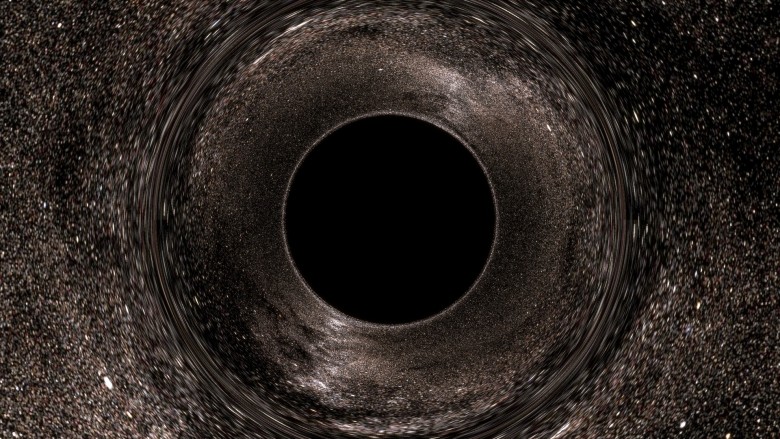
Ini menyoroti fitur-fitur utama: disk hitam dan cincin distorsi yang aneh.

Diskusi sering memperhatikan: salah mengatakan bahwa cakram hitam adalah cakrawala peristiwa. Bahkan, salah mengatakan bahwa area gambar adalah objek . Ini adalah gambar dari suatu objek. Memang, ada lintasan yang, saat melacak dari mata Anda ke sumber, akan muncul di horizon peristiwa (GS). Ini adalah piksel hitam, karena tidak ada foton yang dapat mengikuti jalur ini dari lubang hitam (BH) ke mata Anda. Dengan demikian, cakram hitam ini sangat jelas merupakan citra cakrawala peristiwa , dalam arti bahwa jika Anda menggambar (di masa lalu) sesuatu yang langsung di atas cakrawala, maka pengamat eksternal akan dapat melihatnya langsung di cakram hitam ini (kami sebenarnya akan menjalankan ini coba nanti). Dalam beberapa publikasi, wilayah hitam ini juga disebut "bayangan" BH.



Namun, menarik untuk dicatat bahwa ini juga merupakan gambar dari photon sphere (PS). Grafik gnuplot di bagian atas menggambarkan geodesi dari foton yang masuk dari infinity (melihat BH dari kejauhan saat memperbesar) bersama dengan GS (hitam) dan FS (hijau). Jari-jari bola foton 1,5 kali lebih besar dari jari-jari cakrawala peristiwa (dalam geometri Schwarzschild) dan di sini orbit melingkar dari foton di sekitar lubang hitam diizinkan (walaupun tidak stabil). Pada grafik, beberapa sinar jatuh ke dalam non-keberadaan, sementara yang lain tersebar (dan, dengan demikian, muncul di titik lain di bidang langit). Dapat dilihat bahwa untuk sinar yang diserap, parameter paparan kurang dari ~ 2,5 jari-jari. Ini adalah radius yang jelas dari disk hitam, dan jauh lebih besar daripada GS dan FS.

Bagaimanapun, fakta berikut ini penting:

Insiden sinar cahaya secara bebas di bola foton juga akan mencapai horizon peristiwa.

Ini berarti bahwa gambar bola foton termasuk dalam gambar horizon peristiwa. Tapi karena GS jelas terletak di dalam FS, gambar yang pertama juga harus menjadi bagian dari yang terakhir. Maka kedua gambar harus cocok.

Mengapa kami memverifikasi bahwa disk hitam juga merupakan gambar dari FS? Karena ini berarti tepi disk hitam diisi dengan foton yang meluncur di sepanjang bola foton. Piksel segera di luar cakram hitam sesuai dengan foton, yang (ketika ditelusuri kembali) secara spiral jatuh ke dalam bola foton, semakin dekat dan lebih dekat ke orbit melingkar yang tidak stabil, berputar berkali-kali (semakin dekat Anda melihat, semakin cepat ia berputar), dan kemudian muncul dalam spiral - karena orbitnya tidak stabil - dan lolos hingga tak terbatas.

Perilaku ini akan menyebabkan efek optik yang menarik mirip dengan separatrix dalam sistem yang dinamis. Secara teoritis, jika sinar diluncurkan tepat di sepanjang tepi, itu akan selamanya berputar dalam spiral, lebih dekat dan lebih dekat ke orbit melingkar bola foton.

Pengaruh di bidang surgawi

Kami tidak akan fokus pada topik ini, karena applet terakhir dikhususkan untuk itu, dan itu memberikan ide distorsi yang jauh lebih baik di langit (termasuk opsi kisi UV untuk distorsi yang lebih jelas).

Hanya beberapa kata tentang cincin Einstein. Lensa gravitasi secara optik dapat dibedakan karena merupakan gambar dari satu titik, yang terletak tepat di seberang pengamat. Cincin terbentuk pada sudut pandang seperti itu ketika sinar dari pengamat ditekuk secara paralel. Sinar eksternal tidak cukup melengkung dan tetap berbeda; di dalam mereka membungkuk terlalu banyak, bertemu dan pada kenyataannya bahkan bisa mundur atau dalam lingkaran, seperti yang kita lihat.

Tetapi pikirkan ini: jika Anda cukup dekat dengan cakram hitam, sinar cahaya dapat membuat satu lingkaran, dan kemudian berjalan paralel. Di sana kita harus melihat cincin sekunder Einstein. Bahkan, mungkin ada cincin pesanan apa pun (berliku berapa pun). Seharusnya juga ada cincin "aneh" di antara mereka, di mana sinar cahaya menekuk secara paralel, tetapi diarahkan ke penampil. Serangkaian cincin tanpa akhir ini ada, tetapi benar-benar tidak terlihat dalam gambar kita (pada kenyataannya, dalam sebagian besar gambar ini), karena terlalu dekat dengan tepi disk.

Distorsi horizon acara

Sesuatu telah berubah dalam gambar baru ini. Pertama-tama, ini dibuat dalam resolusi yang lebih baik dan dengan penyaringan latar belakang untuk membuatnya lebih dapat dibedakan. Kemudian saya memperbesar gambar BH (tidak mendekat, kami masih pada jarak ~ 10 jari-jari dari itu, hanya zoom). Tetapi yang paling penting, saya menggambar kotak di cakrawala .

Cakrawala adalah "hanya bola." Secara teknis, ini bukan bola Riemannian standar dengan metrik spasial. Cakrawala seperti cahaya! Ini adalah cara yang penuh warna untuk mengatakan bahwa ia bergerak dengan kecepatan cahaya. Namun, dalam koordinat Schwarzschild, itu masih permukaan $$$r = 1$ dan bisa kita gunakan $$$\ phi$ dan $$$\ theta$ seperti bujur dan lintang. Dengan demikian, sebuah grid dapat digambar dengan cara kanonik. Anda melihatnya dalam gambar.

Kisi memungkinkan Anda untuk melihat efek khusus yang dapat diturunkan jika kami menganalisis kurva hamburan / penyerapan foton di atas:

Seluruh permukaan cakrawala terlihat secara simultan dari titik mana pun.

Ini sangat menarik. Ketika Anda melihat bola tetap dalam ruang-waktu standar yang datar, Anda melihat tidak lebih dari 50% permukaannya setiap saat (jika Anda mendekat, itu kurang dari 50% karena perspektif). Tetapi cakrawala terlihat bersamaan dengan cakram hitam: perhatikan, khususnya, kutub Utara dan Selatan. Namun demikian, meskipun seluruh permukaan ditempatkan pada cakram hitam, itu tidak mencakup seluruhnya : jika Anda memperbesar tepi, Anda akan melihat bahwa gambar GE berakhir di ujung bayangan. Anda akan menemukan cincin yang terletak sangat dekat dengan tepi luar, tetapi tidak sampai akhir. Gambar ini adalah titik yang berlawanan dengan pengamat dan mendefinisikan batas-batas dari gambar "pertama" dari HS di dalam. Jadi, apa antara cincin ini dan tepi sebenarnya? Saya belum membuat gambar yang diperbesar, tetapi ada seluruh gambar lain dari cakrawala acara . Dan kemudian satu lagi, dan satu lagi, hingga tak terbatas. Ada gambar konsentris tak berujung dari seluruh cakrawala, dikompresi dalam bayangan. (Banyak terima kasih / u / xXxDeAThANgEL99xXx untuk menunjukkan fenomena ini yang saya lewatkan) .

Menambahkan disk akresi

Apa yang akan dilakukan rendering BH modern tanpa disk akresi? Meskipun ini jelas merupakan pertanyaan yang dapat diperdebatkan, apakah Interstellar Nolan benar-benar tersedia untuk observasi, belum lagi keakuratannya, tetapi kita harus berterima kasih kepada blockbuster karena telah mempopulerkan distorsi khusus pada disk akresi. Di sini kita memiliki piringan akresi horisontal yang sangat tipis, datar, memanjang dari bola foton (walaupun ini sangat tidak realistis karena orbitnya lebih rendah $$$3r_S$ tidak stabil, seperti dijelaskan di bawah) hingga 4 jari-jari, dicat dalam sangkar putih dan biru. Dengan warna seperti itu, jelas bahwa kita dihadapkan dengan kasus lain, ketika pada saat yang sama 100% dari permukaan objek terlihat.

Untuk gambar ini, saya memindahkan pengamat sedikit lebih tinggi untuk melihat disk sedikit dari atas. Anda melihat gambar dua wajah disk : bagian atas dan bawah. Gambar membungkuk dalam lengkungan di atas bayangan lubang hitam karena balok diarahkan langsung di atas lubang hitam membungkuk untuk memenuhi permukaan atas disk di belakang lubang, di seberang pengamat.

Ini juga menjelaskan keberadaan gambar yang lebih rendah: sinar yang berada di bawah BH tertekuk ke permukaan disk yang lebih rendah, yang berada di belakang BH. Jika Anda melihat lebih dekat, gambar menyebar ke seluruh bayangan, tetapi di bagian atas jauh lebih tipis. Ini sesuai dengan sinar cahaya yang berada di atas BH, membuat lingkaran hampir penuh di sekitar lubang dan mengenai permukaan yang lebih rendah di depan disk.

Tentu saja, mudah untuk menyimpulkan bahwa ada jumlah gambar disk akresi yang tak terbatas yang menipis sangat cepat ketika mereka mendekati tepi. Gambar selanjutnya sudah sangat tipis, hampir tidak terlihat di bagian bawah tepi.

GIF masih relevan

Dalam animasi kejang ini, saya menyalakan / mematikan defleksi cahaya (secara resmi Schwarzschild / Minkowski) untuk mengklarifikasi beberapa poin yang kita bicarakan.





Dua gif aneh ini dibuat atas permintaan pembaca. Pada yang pertama, pengamat melingkari lubang hitam pada jarak 10 jari-jari. Ini seharusnya tidak dipahami sebagai orbit yang sebenarnya, karena pada kenyataannya tidak ada penyimpangan ketika bergerak di orbit. Berikut adalah serangkaian gambar BH diam dari beberapa titik di mana pengamat bergerak dari satu tempat ke tempat di antara bingkai; ini adalah orbit "adiabatik", jika Anda suka.

Dan stereo masih relevan

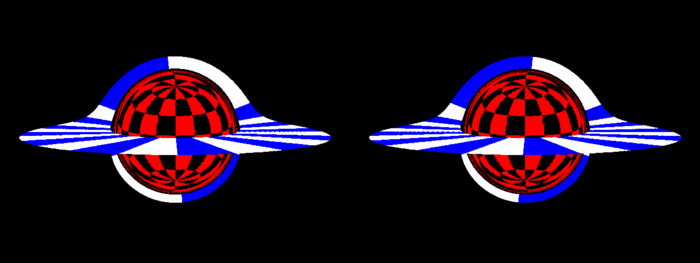
Menariknya, bayang-bayangnya terlihat cukup rata.

Ilmu yang cukup

Kami memiliki cukup gambar informatif dengan gaya tahun 90-an dalam resolusi rendah dengan warna beracun. Berikut adalah beberapa rendering "pop" (klik untuk ukuran penuh).


Gambar ini dihasilkan oleh pengguna / n / dfzxh dengan oversampling empat kali lipat


Rencana yang lebih besar


Gambar cincin yang diperbesar


Efek kultus "cincin cahaya" jika dilihat dari bidang ekuatorial


Jika Anda mengunduh program, maka ini adalah pemandangan saat ini secara default


Drive yang jauh lebih lebar

Ya, tidak ada yang istimewa. Tidak ada karya seni, hanya rendering dari program. Mari kita sementara kembali ke ilmu pengetahuan: gambar ketiga , yang tampaknya tidak memiliki makna, sebenarnya sangat berharga. Ini adalah area yang diperbesar antara tepi atas disk hitam dan gambar utama disk akresi. Pengamat berada di tepi luar dari disk akresi itu sendiri dan memperbesar gambar. Tujuannya adalah untuk menggambarkan sebanyak mungkin dering berbagai pesanan. Tiga urutan terlihat: zona yang lebih terang di bagian atas hanya tepi bawah gambar pertama dari permukaan jauh atas disk. Bilah di bawah ini, di bawah lautan bintang yang terbentang yang tenang, adalah bagian atas dari gambar bagian depan bawah cakram. Di bagian paling bawah - garis tipis cahaya dengan lebar tidak lebih dari satu piksel, terpaku pada cakram hitam bola foton. Ini pada dasarnya adalah gambar ketiga: sekali lagi, permukaan atas yang jauh, tetapi setelah cahaya menyelesaikan revolusi tambahan di sekitar lubang hitam. Digabung dengan itu, tetapi gambar yang semakin tipis adalah cincin dari tingkat yang lebih tinggi. Ya, ini juga layak untuk tag <blockquote>:

Ada gambar tak berujung dari permukaan atas dan bawah dari akresi disk, dan mereka semua menunjukkan seluruh permukaan disk pada saat yang sama. Selain itu, kecuali untuk yang pertama, gambar-gambar ini tidak lewat di depan cakram hitam, atau di depan satu sama lain, dan oleh karena itu “konsentris”.

Luar biasa

Saya menerima permintaan rendering
Tertarik pada visualisasi tertentu, tetapi tidak siap untuk melalui kesulitan menginstal program dan membuat sendiri? Jatuhkan saja aku reddit atau kirimkan aku . Rendering 1080p pada laptop saya membutuhkan waktu tidak lebih dari 10-20 menit.

Disc akresi yang realistis

Disk akresi dalam rendering cukup kartun. Ini hanya disk tekstur bodoh. Apa yang terjadi ketika fisika nyata dimasukkan dalam tampilan visual disk? Apa yang terjadi ketika Anda mempertimbangkan pergeseran merah dari gerakan orbital, misalnya?

Model populer dari piringan akresi adalah piringan materi yang sangat tipis dalam orbit yang hampir bundar. Dimulai dengan ISCO (orbit melingkar stabil paling dalam, $$$3r_s$ ) dengan profil suhu menurut hukum daya $$$(T \ sim r ^ {- a}$ . Saya akan menggunakan opsi yang sangat sederhana:

$$

$$T \ sim r ^ {- 3/4}$$

yang pasti abnormal dalam teori relativitas umum untuk cairan realistis, tetapi ini dia (dalam hal apa pun, Anda tidak akan melihat perbedaannya).

Sekarang parameter bebas adalah skala umum untuk suhu, misalnya, suhu dalam ISCO. Suhu ini sangat besar untuk sebagian besar lubang hitam. Kita berbicara tentang ratusan juta Kelvin; sulit untuk membayangkan artefak manusia yang dapat ada di bawah pengaruh radiasi cakram (puncak radiasi sinar-x) pada suhu seperti itu, belum lagi fotografi. Jadi kita jelas perlu menurunkan suhu. Jelas, lubang hitam supermasif lebih dingin, tetapi tidak cukup. Kita perlu turun ke 10.000 K di ISCO sehingga kita setidaknya bisa melihat sesuatu. Ini sangat tidak akurat, tapi hanya itu yang bisa saya lakukan.

Dua pertanyaan harus ditanyakan. Pertama: apa warna tubuh hitam pada suhu ini? Kedua: seberapa terang itu ? Secara formal, jawaban untuk dua pertanyaan ini adalah dalam produk skalar fungsi yang menggambarkan saluran R, G, B dengan spektrum benda hitam. Dalam praktiknya, beberapa perkiraan digunakan.

Untuk formula Tanner Helland , ini akurat dan efektif untuk warna, tetapi mencakup banyak kondisi yang tidak layak dengan penelusuran sinar saya (lihat di bawah untuk detail lebih lanjut). Cara tercepat adalah dengan menggunakan tekstur sederhana:



Tekstur ini adalah salah satu dari banyak hal yang berguna dalam pemilihan Mitchell Charity tentang "Apa warna tubuh hitam?" . Untuk referensi, ini sesuai dengan titik putih E (whitepoint E).

Skala menunjukkan warna benda hitam pada suhu dari 1000 K hingga 30.000 K, dengan suhu yang lebih tinggi sesuai dengan warna biru yang hampir sama. Karena ada perbedaan besar dalam kecerahan antara suhu, tekstur ini tidak dapat dan tidak mengirimkan kecerahan; melainkan menormalkan warna. Tugas kita adalah menghitung kecerahan relatif dan menerapkannya. Formula analitik cocok untuk ini. Jika kita mengasumsikan bahwa spektrum terlihat sangat sempit, maka intensitas total terlihat sebanding dengan spektrum tubuh hitam itu sendiri:

$$

$$\ frac {1} {\ lambda ^ 5} \ frac {1} {\ exp (\ frac {hc} {\ lambda k_B T}) - 1}$$

di mana saya menyingkirkan konstanta umum yang bodoh (kita masih akan skala kecerahan untuk melihat sesuatu). Anda cukup memasukkan $$$\ lambda$ kira-kira untuk rentang spektrum yang terlihat, dan kami mendapatkan bahwa kecerahannya sebanding dengan suhu menurut rumus ini:

$$

$$(e ^ {\ frac {29622.4 \ text {K}} {T}} - 1) ^ {- 1}$$

Cukup sederhana. Sebagai pemeriksaan, kami mencatat bahwa intensitas relatif turun menjadi nol ketika T mendekati nol, dan secara praktis tidak berubah ketika T berubah menjadi tak terhingga.

Pergeseran merah

Kami membahas kecepatan orbital dalam geometri Schwarzschild dalam deskripsi applet. Untuk menghitung pergeseran merah, rumus pergeseran merah dari SRT digunakan:

$$

$$(1 + z) _ \ text {Doppler} = \ frac {1 - \ beta \ cos (\ theta)} {\ sqrt {1- \ beta ^ 2}}$$

Dimana sebagai $$$\ cos (\ theta)$ - cosinus sudut antara arah sinar yang dipancarkan oleh disk dan kecepatan lokal disk, dihitung dalam sistem koordinat inersia lokal Schwarzschild. Rumusnya benar dalam konteks ini karena prinsip kesetaraan.

Itu harus dikalikan dengan koefisien pergeseran merah gravitasi:

$$

$$(1 + z) _ \ text {Gravitational} = (1 - r ^ {- 1}) ^ {- 1/2}$$

koefisien ini tidak tergantung pada lintasan berkas cahaya, tetapi hanya pada jari-jari radiasi, karena geometri Schwarzschild adalah stasioner.

Ini juga berarti bahwa kontribusi posisi pengamat terhadap pergeseran merah gravitasi adalah konstan di seluruh bidang pandang. Seluruh gambar kami memiliki pergeseran biru umum yang konstan, karena kami jauh di dalam BH. Oleh karena itu, efek ini hanya memberikan warna samar yang dapat diabaikan.

Kami juga mengabaikan pergeseran merah dari gerakan pengamat, karena pengamat kami diam di geometri Schwarzschild. Inilah hasil akhirnya:



Seperti yang Anda lihat, sebagian besar disk benar-benar putih karena kecerahan maksimum di saluran warna. Jika Anda menurunkan saluran ini ke kisaran 0,0-1,0, maka bagian luar disk akan menjadi pucat atau hitam.Peningkatan kecerahan terlalu besar untuk dilihat dan dihargai. Saya mencoba menunjukkan efek menggunakan post-processing sehingga bagian yang paling terang menunjukkan transisi warna, tetapi ini hampir tidak cukup.

Gambar yang cukup membingungkan. Berikut adalah gambar tanpa memperhitungkan kecerahan akun, di mana Anda dapat mengevaluasi warna:



Gambar-gambar ini memiliki resolusi lebih rendah, karena mereka membutuhkan waktu yang sangat lama untuk ditampilkan di laptop saya (akar kuadrat buruk, anak-anak).

Bagaimanapun, render ini seribu kali lebih spektakuler dari yang lain (terutama karena tepi bagian dalam disk sudah cukup jauh dari GS, sehingga pelensanya terlalu besar), tetapi rendernya setidaknya akurat . Jika Anda menemukan lubang hitam dengan suhu 10.000 K dan kacamata hitam yang bagus, Anda akan melihatnya.

Tembakan close-up lainnya. Saya secara tidak wajar meningkatkan kejenuhan untuk kecantikan:

Menulis pelacak sinar lubang hitam

Sumber Github

Ada perbedaan yang sangat besar dan jelas antara optik lubang hitam dan integrator numerik, yang menghasilkan wallpaper desktop yang indah dengan resolusi 1080p. Terakhir kali saya tidak mempublikasikan alasan saya, tetapi hanya mengangkat repositori git yang besar dan kotor. Sekarang saya ingin menjelaskan sedikit lebih detail, dan juga mencoba mempertahankan kode dalam bentuk yang lebih akurat dan dengan komentar.

Pelacak saya tidak dibuat bagus, kuat, cepat. Pertama-tama, saya ingin membuatnya mudah diatur, untuk membuatnya sederhana, sehingga orang bisa mendapatkan inspirasi dan melihat potensi peningkatan: bahkan ketidaksempurnaannya dapat mendorong seseorang untuk memutuskan untuk menulis versi mereka sendiri. Berikut ini adalah ikhtisar singkat dari algoritma dan implementasinya.

Potensi "Ajaib"

Jadi, teori relativitas umum, semuanya jelas. Itu mudah. Kami mengambil metrik Schwarzschild, mencari simbol Christoffel, menghitung turunannya, menuliskan persamaan geodesik, mengubah beberapa koordinat Cartesian untuk menghindari penderitaan tanpa akhir, dapatkan ODE multi-garis besar, selesaikan. Sesuatu seperti itu.

Hanya bercanda Tentu saja ada satu trik.

Jika Anda ingat, terakhir kali saya mendapatkan persamaan berikut untuk orbit partikel tak bermassa di bidang orbitnya dalam geometri Schwarzschild ($$u = 1 / r ):$u=1/r$

$$

$$u''(\phi) + u = \frac{3}{2} u^3$$

Caranya adalah dengan melihat rumus Binet di sini . Untuk massa partikel Newtonian dalam potensi Newtonian medan gaya pusat:

$$

$$\frac{d^2}{dt^2} \vec x = \frac{1}{m} F(r)$$

maka partikel jelas akan bergerak dalam bidang orbitalnya dan sesuai dengan rumus Binet untuk $$$u(\phi)$ :

$$

$$u'' + u = - \frac{1}{m h^2 u^2} F(u)$$

Dimana $$$\frac{d}{d\phi}$ Adalah bilangan prima $$$m$ - massa, dan $$$h$- momentum sudut per satuan massa. Ini adalah persamaan untuk orbit, bukan persamaan gerak. Itu tidak mengatakan apa-apa tentang$$$u(t)$ atau $$$phi(t)$ hanya menunjukkan hubungan antara $$$u$ dan $$$\phi$ .

Mari kita berhenti sejenak untuk merenungkan apa yang sebenarnya kita dapatkan. Persamaannya mengatakan bahwa jika Anda membayangkan sistem mekanis hipotetis suatu partikel di bawah aksi gaya pusat tertentu, maka lintasannya akan menjadi solusi dari rumus Binet. Kemudian sistem mekanik menjadi formula kalkulator.

Itulah yang saya tawarkan di sini. Kami telah mengindikasikan$$$m=1$ dan mereka mengambil (non-fisik, apa pun) sistem sederhana partikel titik dalam medan gaya khusus ini:

$$

$$\vec F(r) = - \frac{3}{2} h^2 \frac{\hat r}{r^5}$$

dimana $$$h$Merupakan konstanta tertentu, dan menyelesaikan persamaan secara numerik sangat sederhana. Lalu solusinya$$$\vec x (T)$ dimana $$$T$ - koordinat waktu abstrak untuk sistem ini, pada kenyataannya, parameterisasi dari satu-satunya solusi untuk persamaan Binet yang sesuai, yang merupakan persamaan geodesik .

Oleh karena itu, kami memecahkan persamaan Newtonian dalam koordinat Cartesian, yang umumnya paling sederhana (saya memutuskan untuk menggunakan metode Runge-Kutta sehingga akan mungkin untuk meningkatkan ukuran langkah dan mengurangi waktu rendering, tetapi di masa depan pengguna akan dapat memilih metode solusi yang berbeda). Lalu kita dapatkan geodesi seperti cahaya yang sebenarnya, di mana $$$T$ Apakah parameter berjalan bersama (berbeda dengan Schwarzschild $$$t$ , dan dari waktu normal, yang tidak ada).

Ini jauh lebih baik daripada metode sebelumnya, yang bekerja dengan koordinat kutub di bidang orbit. Di sini perhitungannya sangat efisien.

Ray melacak dengan numpy

Jika Anda melihat sumbernya, Anda akan melihat skrip Python. Horor! Mengapa menulis ray tracing dengan Python? Semua orang tahu betapa lambatnya loop dijalankan dengan Python, yang selalu (hampir) mengakhiri kerja. Faktanya adalah kita melakukan perhitungan secara numpy - dan secara paralel. Itu sebabnya program ini tidak akan dapat secara bertahap menampilkan bagian-bagian yang sudah ditarik di layar: itu membuat semuanya pada saat yang sama.

Pertama-tama, kami membuat berbagai kondisi awal. Misalnya, array (numPixel, 3) dengan vektor untuk semua piksel dalam gambar (numPixel - lebar gambar × tinggi gambar). Kemudian perhitungan setiap sinar direduksi menjadi array jenis (numPixel, ...) . Karena operasi dengan array dalam numpy sangat cepat, dan semuanya diketik secara statis di sini (saya harap saya tidak mengatakan sesuatu yang bodoh sekarang), itu harus dihitung dengan cukup cepat. Mungkin bukan C, tapi masih cepat. Pada saat yang sama, kami memiliki fleksibilitas dan kejelasan Python.

Metode ini mengerikan untuk penelusuran sinar standar, di mana objek memiliki bagian yang difus, memantulkan, dan membiaskan dan penting untuk mempertimbangkan kondisi pencahayaan. Sebagai contoh, refleksi selektif dari bagian-bagian dari array sinar adalah mimpi buruk yang nyata; melacak nilai boolean atau indeks loop membutuhkan banyak mask, dan loop tidak dapat dipatahkan. Tapi di sini ada kasus lain: semua benda di pemandangan kita hanya memancarkan cahaya: langit, piringan akresi panas, cakrawala peristiwa hitam pekat, dan debu cerah. Mereka tidak terpengaruh oleh cahaya kejadian, dan cahaya itu sendiri dengan tenang melewati mereka, kecuali untuk mengurangi intensitas. Ini membawa kita ke sebuah algoritma untuk menentukan warna:

Pencampuran warna

Ini mudah: Anda hanya perlu mencampur semua objek di antara kami dan sumber sinar dengan nilai alpha yang sesuai, dan menempatkannya di atas satu sama lain, di mana yang terjauh akan berada di bagian bawah. Kami menginisialisasi buffer warna dengan alpha-transparan hitam, maka ketika kami berpotongan dengan objek kami memperbarui buffer dengan mencampur warna dari objek di bawah buffer warna kami. Kami melakukan langkah yang sama untuk debu (gunakan profil kerapatan $$$r ^ {- 2}$ ) dan terus beralih ke akhir. Perhatikan bahwa saluran alpha juga berfungsi sebagai Z-buffer, karena objek berhenti berkontribusi setelah sinar melintasi objek buram (yang dengan demikian mengatur nilai alpha buffer ke 1.0).

Kelemahan yang jelas dari metode ini adalah bahwa Anda tidak dapat menghentikan ray tracing setelah menghitungnya, karena ini adalah bagian dari array di mana penelusuran sinar lain berlanjut. Misalnya, setelah tabrakan dengan horizon, sinar terus mengembara secara acak setelah mereka jatuh ke singularitas - Anda dapat melihat apa yang terjadi jika Anda secara eksplisit mematikan objek horizon. Algoritma alpha blending memastikan bahwa mereka tidak mempengaruhi gambar akhir, tetapi sinar ini masih memuat CPU.