Meratakan titik secara merata di seluruh bidang dalam pytorch dan tensorflow

Teks ini ditulis untuk mereka yang tertarik dalam pembelajaran yang mendalam, yang ingin menggunakan metode yang berbeda dari perpustakaan pytorch dan tensorflow untuk meminimalkan fungsi banyak variabel, yang tertarik untuk belajar bagaimana mengubah program yang dijalankan secara berurutan menjadi perhitungan matriks vektor yang dilakukan menggunakan numpy. Anda juga dapat mempelajari cara membuat kartun dari data yang divisualisasikan menggunakan PovRay dan vapory.

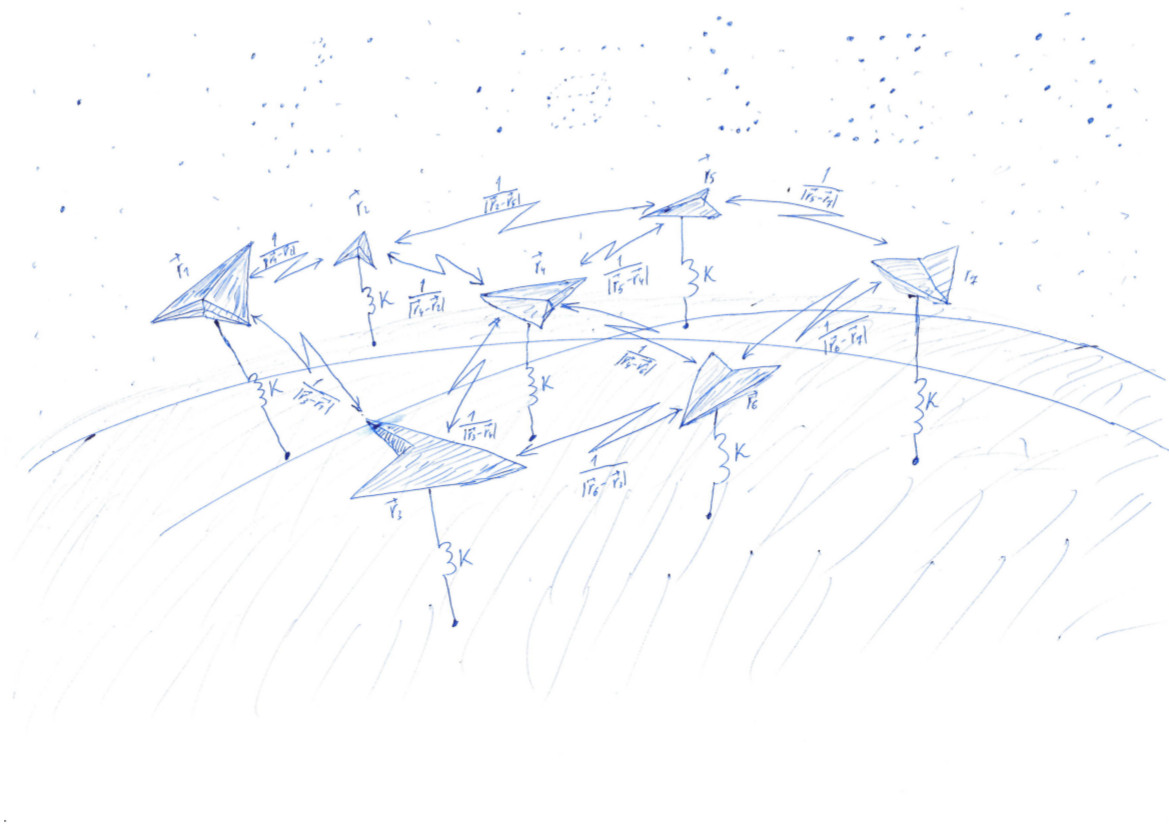
Di mana tugas dari

Masing-masing meminimalkan fungsinya (c) Anonim Data Scientist

Dalam salah satu publikasi sebelumnya dari blog kami , yaitu di paragraf "Rake No. 6", kami berbicara tentang teknologi DSSM, yang memungkinkan Anda mengonversi teks menjadi vektor. Untuk menemukan pemetaan seperti itu, kita perlu menemukan koefisien transformasi linear yang meminimalkan fungsi kerugian yang agak rumit. Memahami apa yang terjadi ketika mempelajari model seperti itu sulit karena dimensi besar vektor. Untuk mengembangkan intuisi yang memungkinkan Anda memilih metode optimasi dan mengatur parameter metode ini, Anda dapat mempertimbangkan versi sederhana dari tugas ini. Sekarang biarkan vektor berada di ruang tiga dimensi kita yang biasa, maka mereka mudah untuk menggambar. Dan fungsi kerugian akan menjadi potensi untuk mendorong titik terpisah dan menarik ke unit sphere. Dalam hal ini, solusi untuk masalah ini adalah distribusi titik-titik yang merata di atas bola. Kualitas solusi saat ini mudah dievaluasi dengan mata.

Jadi, kami akan mencari distribusi yang seragam pada lingkup jumlah yang diberikan $$$n$poin. Distribusi semacam itu kadang-kadang diperlukan untuk akustik untuk memahami ke arah mana meluncurkan gelombang dalam kristal. Signalman - untuk mengetahui cara menempatkan satelit di orbit untuk mencapai komunikasi kualitas terbaik. Ahli meteorologi - untuk penempatan stasiun pemantauan cuaca.

Untuk beberapa $$$n$tugas diselesaikan dengan mudah . Misalnya, jika $$$n = 8$, kita dapat mengambil kubus dan simpulnya akan menjadi jawaban untuk masalah tersebut. Kami juga beruntung jika $$$n$akan sama dengan jumlah simpul icosahedron, dodecahedron, atau padatan Platonik lainnya. Kalau tidak, tugasnya tidak sesederhana itu.

Untuk jumlah poin yang cukup besar, ada rumus dengan koefisien yang dipilih secara empiris , beberapa opsi lagi ada di sini , di sini , di sini , dan di sini . Tetapi ada solusi yang lebih universal, meskipun lebih kompleks, yang dikhususkan untuk artikel ini.

Kami memecahkan masalah yang sangat mirip dengan masalah Thomson ( wiki ). Menyebarkan $$$n$poin secara acak, dan kemudian membuat mereka menarik ke permukaan, seperti bola, dan mendorong satu sama lain. Daya tarik dan tolakan ditentukan oleh fungsi - potensial. Pada nilai minimum dari fungsi potensial, titik-titik akan terletak pada bidang yang paling merata.

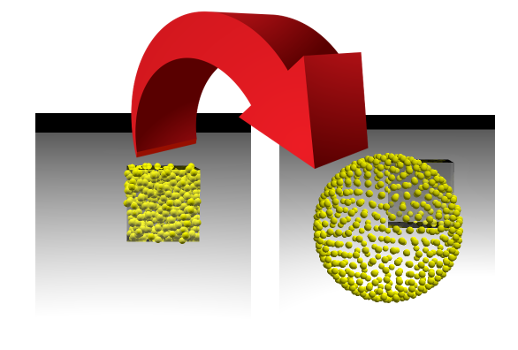
Tugas ini sangat mirip dengan proses pembelajaran model pembelajaran mesin (ML), di mana fungsi kerugian diminimalkan. Tetapi seorang ilmuwan data biasanya mengamati bagaimana angka tunggal menurun, dan kita dapat menyaksikan perubahan gambar. Jika kita berhasil, kita akan melihat bagaimana titik-titik ditempatkan secara acak di dalam kubus dengan sisi 1 menyimpang di sepanjang permukaan bola:

Secara skematis, algoritma untuk memecahkan masalah dapat direpresentasikan sebagai berikut. Setiap titik yang terletak di ruang tiga dimensi sesuai dengan deretan matriks $$$X$. Fungsi kerugian dihitung dari matriks ini. $$$L$, nilai minimum yang sesuai dengan distribusi titik yang seragam di atas bola. Nilai minimum ditemukan menggunakan pytorch dan tensorflow , yang memungkinkan menghitung gradien fungsi kerugian oleh matriks $$$X$dan turun ke minimum menggunakan salah satu metode yang diterapkan di perpustakaan: SGD, ADAM, ADAGRAD, dll.

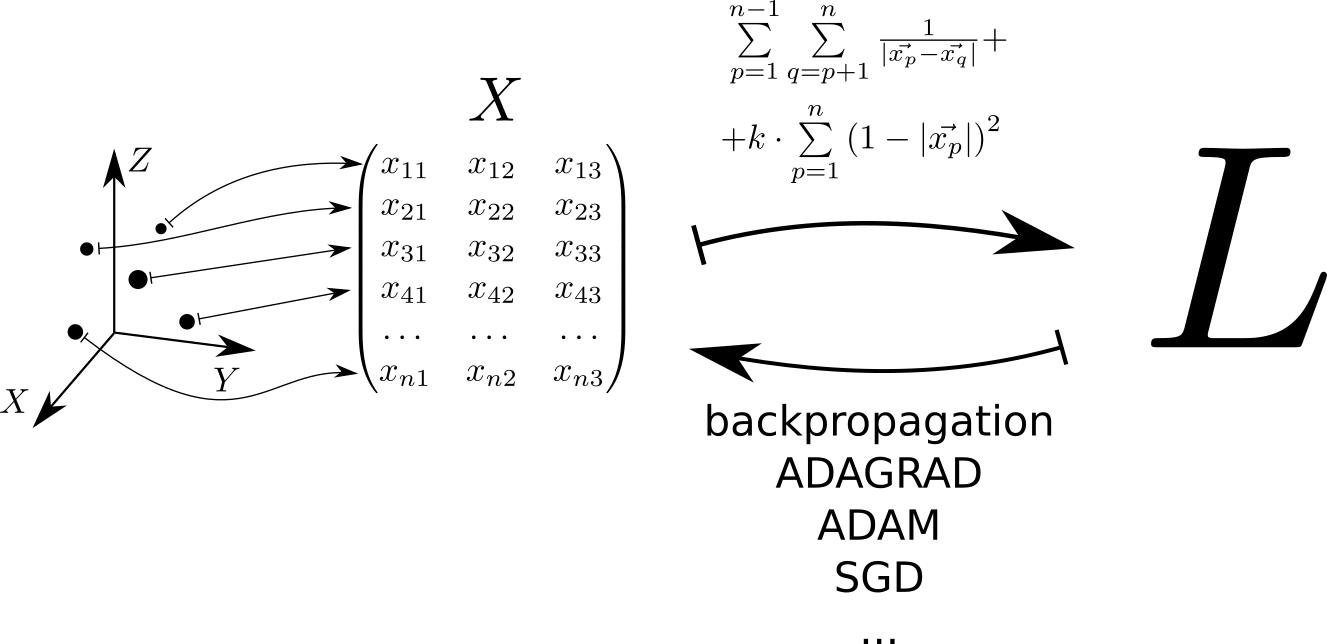
Kami mempertimbangkan potensinya

Karena kesederhanaan, ekspresif, dan kemampuan untuk berfungsi sebagai antarmuka ke perpustakaan yang ditulis dalam bahasa lain, Python banyak digunakan untuk memecahkan masalah pembelajaran mesin. Oleh karena itu, contoh kode dalam artikel ini ditulis dalam Python. Untuk perhitungan matriks cepat, kita akan menggunakan perpustakaan numpy. Untuk meminimalkan fungsi banyak variabel - pytorch dan tensorflow.

Kami secara acak menyebarkan poin dalam kubus dengan sisi 1. Mari kita memiliki 500 poin, dan interaksi elastis 1000 kali lebih signifikan daripada elektrostatik:

 import numpy as np n = 500 k = 1000 X = np.random.rand(n, 3) 

Kode ini menghasilkan matriks $$$X$ukurannya $$$3 \ kali n$diisi dengan angka acak dari 0 hingga 1:

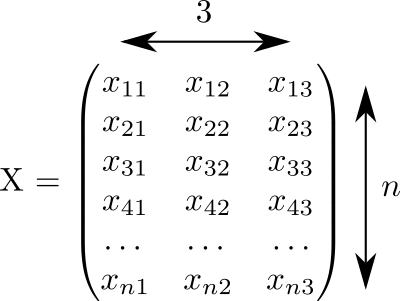
Kami berasumsi bahwa setiap baris matriks ini sesuai dengan satu titik. Dan dalam tiga kolom koordinat dicatat $$$x, y, z$semua poin kami.

Potensi interaksi elastis suatu titik dengan permukaan suatu unit bola $$$u_1 = k \ cdot (1 - r) ^ 2/2$. Potensi interaksi elektrostatik poin $$$p$dan $$$q$- $$$u_2 = 1 / | r_p - r_q |$. Potensi penuh terdiri dari interaksi elektrostatik semua pasangan titik dan interaksi elastis setiap titik dengan permukaan bola:

$$

$$U (x_1, ..., x_n) = \ jumlah \ batas _ {p = 1} ^ {n - 1} \ jumlah \ batas _ {q = p + 1} ^ {n} \ frac 1 {\ kiri | \ vec {x_p} - \ vec {x_q} \ right | } + k \ cdot \ jumlah \ batasan _ {p = 1} ^ n \ kiri (1 - | \ vec {x_p} | \ kanan) ^ 2 \ rightarrow \ min$$

Pada prinsipnya, nilai potensial dapat dihitung menggunakan rumus ini:

 L_for = 0 L_for_inv = 0 L_for_sq = 0 for p in range(n): p_distance = 0 for i in range(3): p_distance += x[p, i]**2 p_distance = math.sqrt(p_distance) L_for_sq += k * (1 - p_distance)**2 #     ,     for q in range(p + 1, n): if q != p: pq_distance = 0 for i in range(3): pq_distance += (x[p, i] - x[q, i]) ** 2 pq_distance = math.sqrt(pq_distance) L_for_inv += 1 / pq_distance #      L_for = (L_for_inv + L_for_sq) / n print('loss =', L_for) 

Tapi ada sedikit masalah. Untuk 2000 poin yang menyedihkan, program ini akan berjalan selama 2 detik. Akan jauh lebih cepat jika kita menghitung nilai ini menggunakan perhitungan matriks vektor. Akselerasi dicapai baik melalui implementasi operasi matriks menggunakan bahasa "cepat" fortran dan C, dan melalui penggunaan operasi prosesor vektor yang memungkinkan melakukan tindakan pada sejumlah besar data input dalam satu siklus clock.

Mari kita lihat matriksnya $$$S = X \ cdot X ^ T$. Ini memiliki banyak sifat yang menarik dan sering ditemukan dalam perhitungan yang berkaitan dengan teori pengklasifikasi linier dalam ML. Jadi, jika kita asumsikan di baris matriks $$$X$dengan indeks $$$p$dan $$$q$vektor ruang tiga dimensi ditulis $$$\ vec {r _ p}, \ vec {r_q}$kemudian matriks $$$S$akan terdiri dari produk skalar dari vektor-vektor ini. Vektor seperti itu $$$n$potongan, maka dimensi dari matriks $$$S$sama dengan $$$n \ kali n$.

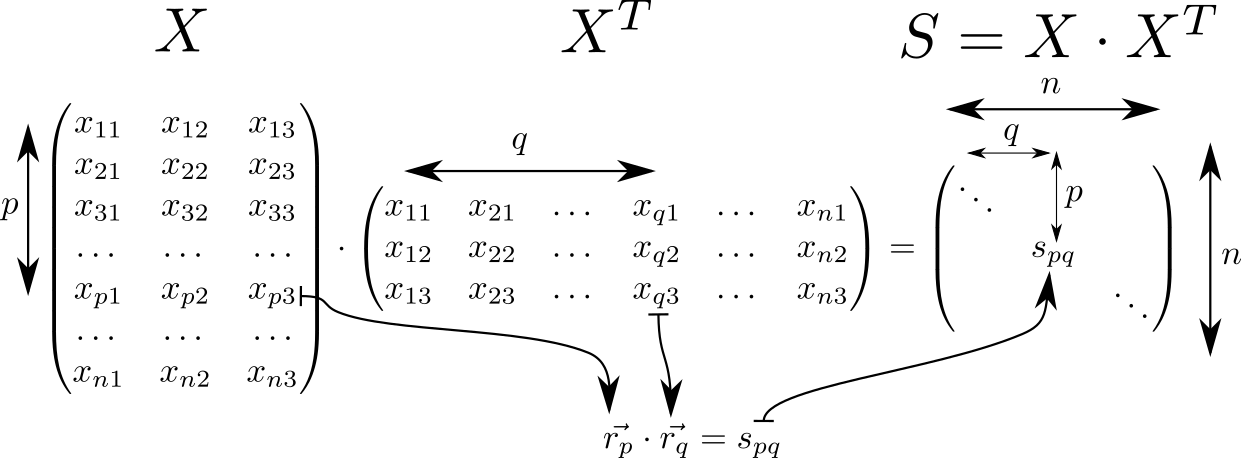
Diagonal dari matriks $$$S$kotak persegi panjang vektor $$$\ vec {r_p}: s_ {p p} = r_p ^ 2$. Mengetahui hal ini, mari kita pertimbangkan potensi penuh interaksi. Kami mulai dengan menghitung dua matriks bantu. Dalam satu matriks diagonal $$$S$akan diulang dalam baris, di kolom lain - dalam.

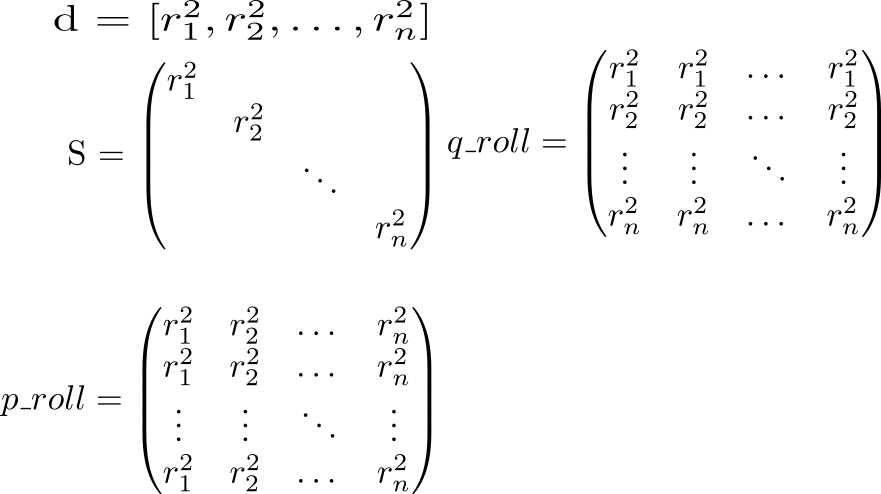
Sekarang mari kita lihat nilai ekspresi p_roll + q_roll - 2 * S

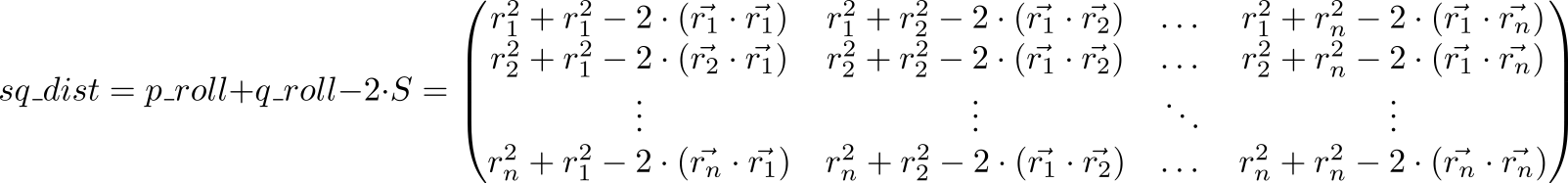
Item yang diindeks $$$(p, q)$matriks sq_dist sama $$$r_p ^ 2 + r_q ^ 2 - 2 \ cdot (\ vec {r_p}, \ vec {r_q}) = (\ vec {r_p} - \ vec {r_q}) ^ 2$. Artinya, kami memiliki matriks kuadrat jarak antar titik.

Tolak elektrostatik pada bola

dist = np.sqrt(sq_dist) - matriks jarak antar titik. Kita perlu menghitung potensi, dengan mempertimbangkan tolakan poin antara mereka sendiri dan daya tarik ke bola. Letakkan unit di diagonal dan ganti setiap elemen dengan kebalikannya (jangan berpikir bahwa kita membalikkan matriks!): rec_dist_one = 1 / (dist + np.eye(n)) . Hasilnya adalah matriks pada diagonal di mana ada unit, elemen lainnya adalah potensi interaksi elektrostatik antara titik-titik.

Sekarang kita menambahkan potensi tarik kuadratik ke permukaan unit sphere. Jarak dari permukaan bola $$$(1 - r)$. Kuadratkan dan lipat dengan $$$k$, yang mendefinisikan hubungan antara peran tolakan elektrostatik partikel dan tarikan bola. Total k = 1000 , all_interactions = rec_dist_one - torch.eye(n) + (d.sqrt() - torch.ones(n))**2 . Fungsi kerugian yang ditunggu-tunggu, yang akan kami meminimalkan: t = all_interactions.sum()

Program yang menghitung potensi menggunakan perpustakaan numpy:

 S = X.dot(XT) #    pp_sq_dist = np.diag(S) #  p_roll = pp_sq_dist.reshape(1, -1).repeat(n, axis=0) #     q_roll = pp_sq_dist.reshape(-1, 1).repeat(n, axis=1) #     pq_sq_dist = p_roll + q_roll - 2 * S #      pq_dist = np.sqrt(pq_sq_dist) #    pp_dist = np.sqrt(pp_sq_dist) #      surface_dist_sq = (pp_dist - np.ones(n)) ** 2 #       rec_pq_dist = 1 / (pq_dist + np.eye(n)) - np.eye(n) #      L_np_rec = rec_pq_dist.sum() / 2 #     L_np_surf = k * surface_dist_sq.sum() #       L_np = (L_np_rec + L_np_surf) / n #   ,     print('loss =', L_np) 

Di sini segalanya sedikit lebih baik - 200 ms pada 2000 poin.

Kami menggunakan pytorch:

 import torch pt_x = torch.from_numpy(X) # pt_x -   tensor   pytorch pt_S = pt_x.mm(pt_x.transpose(0, 1)) # mm - matrix multiplication pt_pp_sq_dist = pt_S.diag() pt_p_roll = pt_pp_sq_dist.repeat(n, 1) pt_q_roll = pt_pp_sq_dist.reshape(-1, 1).repeat(1, n) pt_pq_sq_dist = pt_p_roll + pt_q_roll - 2 * pt_S pt_pq_dist = pt_pq_sq_dist.sqrt() pt_pp_dist = pt_pp_sq_dist.sqrt() pt_surface_dist_sq = (pt_pp_dist - torch.ones(n, dtype=torch.float64)) ** 2 pt_rec_pq_dist = 1/ (pt_pq_dist + torch.eye(n, dtype=torch.float64)) - torch.eye(n, dtype=torch.float64) L_pt = (pt_rec_pq_dist.sum() / 2 + k * pt_surface_dist_sq.sum()) / n print('loss =', float(L_pt)) 

Dan akhirnya tensorflow:

 import tensorflow as tf tf_x = tf.placeholder(name='x', dtype=tf.float64) tf_S = tf.matmul(tf_x, tf.transpose(tf_x)) tf_pp_sq_dist = tf.diag_part(tf_S) tf_p_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (1, -1)), (n, 1)) tf_q_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (-1, 1)), (1, n)) tf_pq_sq_dist = tf_p_roll + tf_q_roll - 2 * tf_S tf_pq_dist = tf.sqrt(tf_pq_sq_dist) tf_pp_dist = tf.sqrt(tf_pp_sq_dist) tf_surface_dist_sq = (tf_pp_dist - tf.ones(n, dtype=tf.float64)) ** 2 tf_rec_pq_dist = 1 / (tf_pq_dist + tf.eye(n, dtype=tf.float64)) - tf.eye(n, dtype=tf.float64) L_tf = (tf.reduce_sum(tf_rec_pq_dist) / 2 + k * tf.reduce_sum(tf_surface_dist_sq)) / n glob_init = tf.local_variables_initializer() #     with tf.Session() as tf_s: #     glob_init.run() #   res, = tf_s.run([L_tf], feed_dict={tf_x: x}) #   print(res) 

Bandingkan kinerja ketiga pendekatan ini:

N	ular sanca	numpy	pytorch	tensorflow
2000	4.03	0,083	1.11	0,205
10.000	99	2.82	2.18	7.9

Perhitungan vektor memberikan keuntungan lebih dari satu setengah desimal relatif terhadap kode python murni. "Pelat ketel" dalam pytorch terlihat: perhitungan volume kecil membutuhkan waktu yang nyata, tetapi hampir tidak berubah dengan meningkatnya volume perhitungan.

Visualisasi

Saat ini, data dapat divisualisasikan menggunakan sejumlah besar paket, seperti Matlab, Wolfram Mathematica, Maple, Matplotlib, dll., Dll. Dalam paket ini ada banyak fungsi kompleks yang melakukan hal-hal kompleks. Sayangnya, jika Anda menghadapi tugas yang sederhana namun tidak standar, Anda tidak bersenjata. Solusi favorit saya dalam situasi ini adalah povray. Ini adalah program yang sangat kuat yang biasanya digunakan untuk membuat gambar fotorealistik, tetapi dapat digunakan sebagai "assembler of visualization." Biasanya, tidak peduli seberapa sulit permukaan yang ingin Anda tampilkan, minta povray untuk menggambar bola dengan pusat-pusat yang terletak di permukaan itu.

Dengan menggunakan perpustakaan vapory, Anda dapat membuat adegan povray langsung dengan python, merendernya dan melihat hasilnya. Sekarang terlihat seperti ini:

Gambar diperoleh sebagai berikut:

 import vapory from PIL import Image def create_scene(moment): angle = 2 * math.pi * moment / 360 r_camera = 7 camera = vapory.Camera('location', [r_camera * math.cos(angle), 1.5, r_camera * math.sin(angle)], 'look_at', [0, 0, 0], 'angle', 30) light1 = vapory.LightSource([2, 4, -3], 'color', [1, 1, 1]) light2 = vapory.LightSource([2, 4, 3], 'color', [1, 1, 1]) plane = vapory.Plane([0, 1, 0], -1, vapory.Pigment('color', [1, 1, 1])) box = vapory.Box([0, 0, 0], [1, 1, 1], vapory.Pigment('Col_Glass_Clear'), vapory.Finish('F_Glass9'), vapory.Interior('I_Glass1')) spheres = [vapory.Sphere( [float(r[0]), float(r[1]), float(r[2])], 0.05, vapory.Texture(vapory.Pigment('color', [1, 1, 0]))) for r in x] return vapory.Scene(camera, objects=[light1, light2, plane, box] + spheres, included=['glass.inc']) for t in range(0, 360): flnm = 'out/sphere_{:03}.png'.format(t) scene = create_scene(t) scene.render(flnm, width=800, height=600, remove_temp=False) clear_output() display(Image.open(flnm)) 

Dari banyak file, gif animasi dirakit menggunakan ImageMagic:

 convert -delay 10 -loop 0 sphere_*.png sphere_all.gif 

Di github Anda dapat melihat kode yang berfungsi, yang fragmennya diberikan di sini. Pada artikel kedua, saya akan berbicara tentang cara mulai meminimalkan fungsional sehingga poin keluar dari kubus dan menyebar secara merata di seluruh bidang.