Ada sejumlah tugas di mana kisaran nilai output harus dibatasi, sementara data input tidak dapat menjamin hal ini. Selain situasi yang dipaksakan, batasan sinyal dapat menjadi tugas yang berorientasi pada tujuan, misalnya, saat mengompresi sinyal atau menerapkan efek "overdrive".
Implementasi kendala yang paling sederhana adalah memaksanya ke nilai tertentu jika level tertentu terlampaui. Misalnya, untuk sinusoid dengan peningkatan amplitudo, akan terlihat seperti ini:

Di sini, fungsi Klip bertindak sebagai pembatas, sebagai argumen di mana sinyal input dan parameter pembatasan ditransmisikan, dan hasil dari fungsinya adalah sinyal output.
Mari kita lihat grafik fungsi klip secara terpisah:
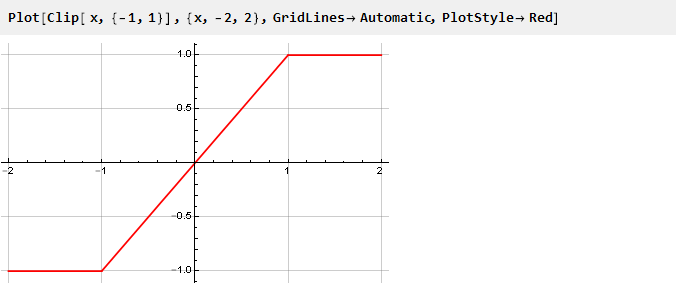
Dapat dilihat dari itu bahwa sementara kita tidak melebihi batas batas, nilai output sama dengan input dan sinyal tidak berubah; ketika terlampaui, nilai output tidak bergantung pada input dengan cara apa pun dan tetap pada level yang sama. Bahkan, kami memiliki fungsi kontinu piecewise yang terdiri dari tiga lainnya: y = -1, y = x dan y = 1, dipilih tergantung pada argumen, dan setara dengan notasi berikut:

Transisi antar fungsi terjadi secara mendadak; dan terlihat menggoda untuk membuatnya lebih halus. Secara matematis, ketajaman ini disebabkan oleh fakta bahwa turunan dari fungsi pada titik docking tidak bersamaan. Ini mudah dilihat dengan memplot turunan dari fungsi Klip:
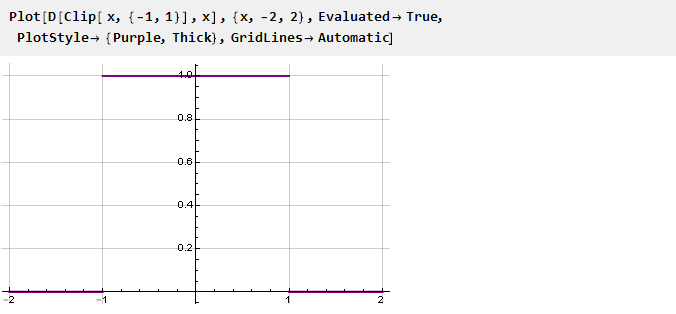
Dengan demikian, untuk memastikan kelancaran fungsi kendala, perlu untuk memastikan kesetaraan turunan pada titik-titik bergabung. Dan karena fungsi ekstrem yang kita miliki adalah konstanta, turunannya sama dengan nol, maka fungsi pembatasan yang diturunkan pada titik-titik docking juga harus sama dengan nol. Selanjutnya, kami akan mempertimbangkan beberapa fungsi ini yang memastikan docking mulus.
Sinus
Yang paling sederhana adalah menggunakan fungsi sin pada interval dari -pi / 2 ke pi / 2, pada batas-batas yang nilai turunannya sama dengan nol menurut definisi:
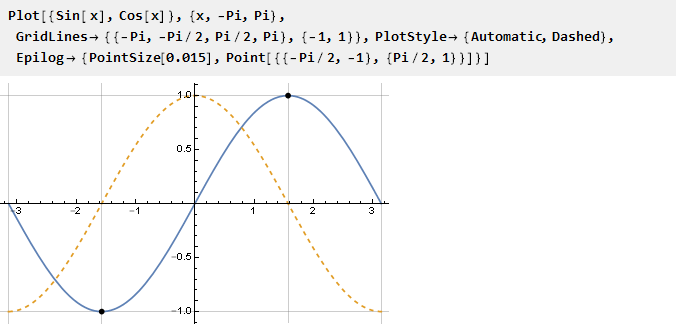
Anda hanya perlu skala argumen sehingga unit diproyeksikan ke Pi / 2. Sekarang kita dapat mendefinisikan fungsi bounding itu sendiri:

Dan buat jadwalnya:
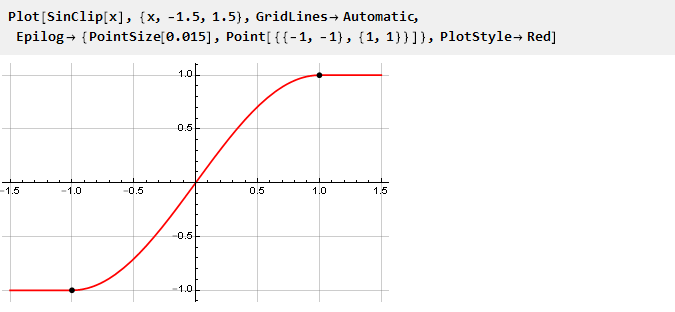
Karena batas dari batasan kami ditentukan secara ketat, batasan tersebut ditetapkan dengan menskalakan sinyal input dengan penskalaan berikutnya (jika perlu).
Juga tidak ada lagi situasi di mana sinyal input ditransmisikan ke output tanpa distorsi - semakin rendah tingkat gain, semakin rendah tingkat distorsi karena batasan - tetapi sinyal terdistorsi dalam hal apa pun.
Efek dari parameter penguatan pada distorsi sinyal juga dapat dilihat dalam dinamika:

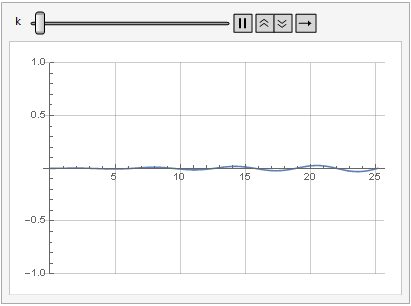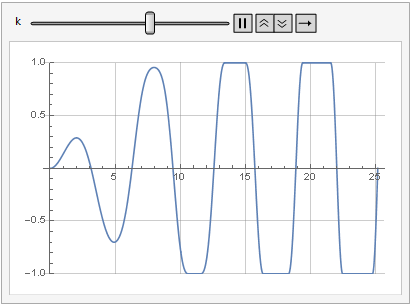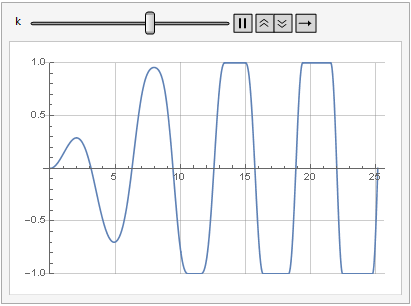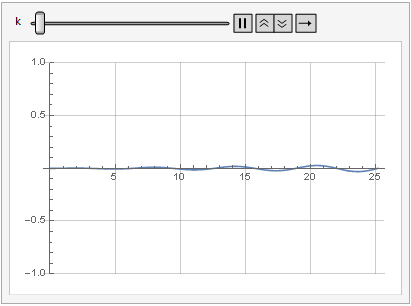
Lebih halus
Mari kita lihat turunan dari fungsi kita:
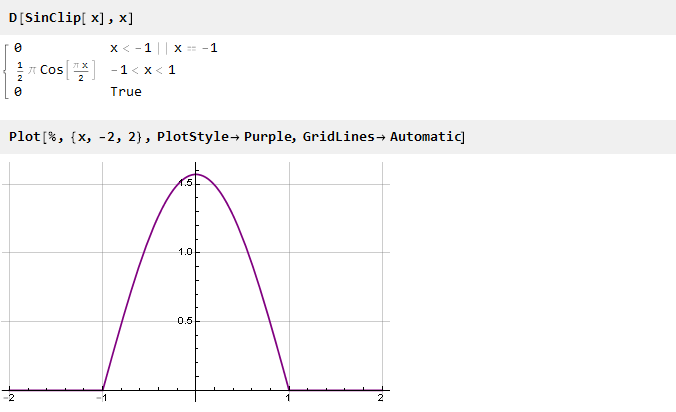
Itu tidak lagi memiliki kesenjangan dalam nilai-nilai, tetapi ada kesenjangan dalam turunannya (yang kedua, jika kita hitung dari fungsi aslinya). Untuk menghilangkannya, Anda bisa pergi ke arah sebaliknya - pertama bentuk turunan yang halus, dan kemudian mengintegrasikannya untuk mendapatkan fungsi yang diinginkan.
Cara termudah untuk membatalkan turunan pada titik -1 dan 1 adalah dengan hanya menyamakan fungsi - semua nilai negatif dari fungsi akan menjadi positif dan, oleh karena itu, akan ada ekses pada titik-titik persimpangan fungsi dengan nol.
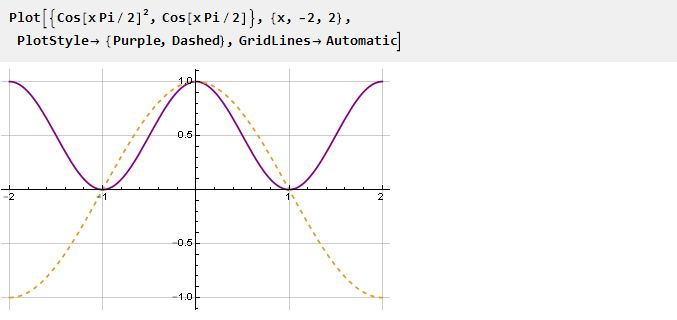
Temukan antiderivatif:
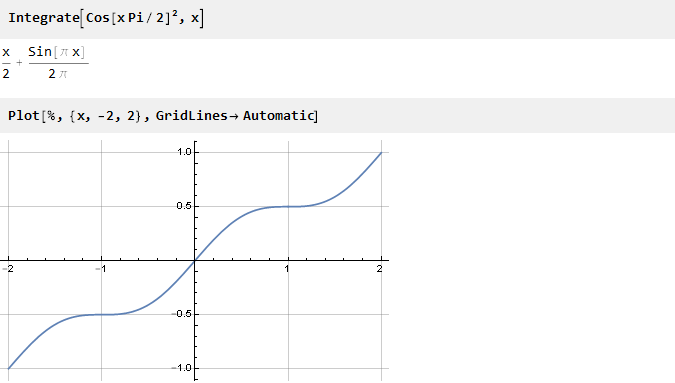
Sekarang skala itu tetap di sepanjang sumbu ordinat. Untuk melakukan ini, cari nilainya di poin 1:

Dan bagi dengan itu (ya, khusus di sini ini adalah perkalian dasar dengan 2, tetapi ini tidak selalu terjadi):

Dengan demikian, fungsi pembatasan akhir akan berbentuk:
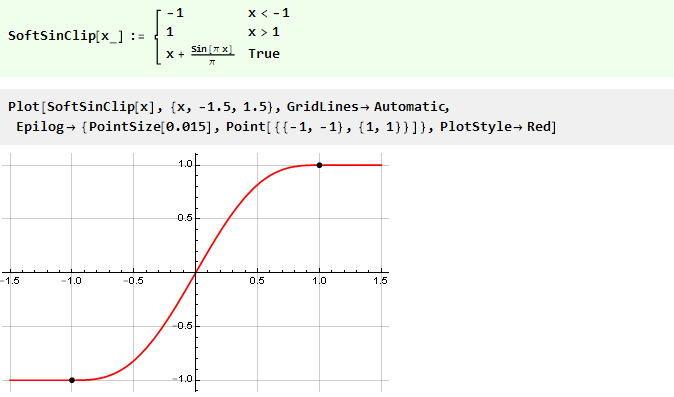
Kami lolos ke polinomial
Menggunakan fungsi trigonometri dalam beberapa kasus bisa jadi agak boros. Oleh karena itu, kami akan mencoba membangun fungsi yang kami butuhkan, tetap dalam kerangka operasi matematika dasar.
Pertimbangkan parabola:
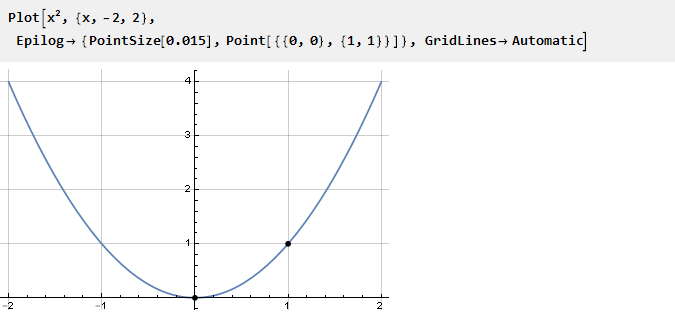
Karena sudah memiliki belok pada titik nol, kita dapat menggunakan bagian yang sama pada interval {0,1} untuk docking dengan konstanta. Untuk nilai negatif, itu perlu digeser ke bawah dan ke kiri:

dan untuk positif - mencerminkan secara vertikal dan horizontal:

Dan fungsi kita dengan parabola akan berbentuk:
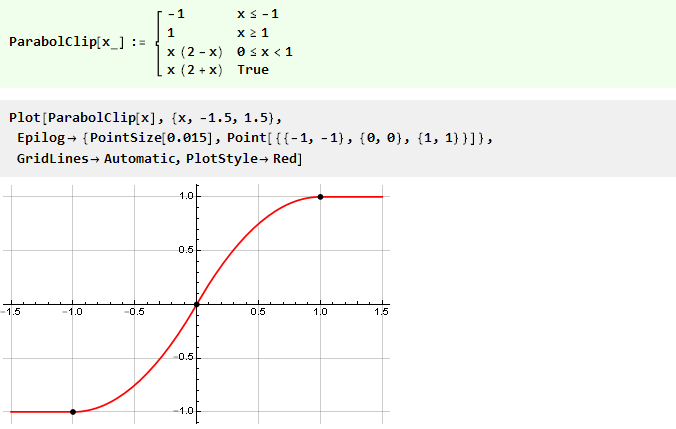
Mari kita sedikit rumit
Mari kita kembali ke parabola kita, balikkan dan geser satu unit:
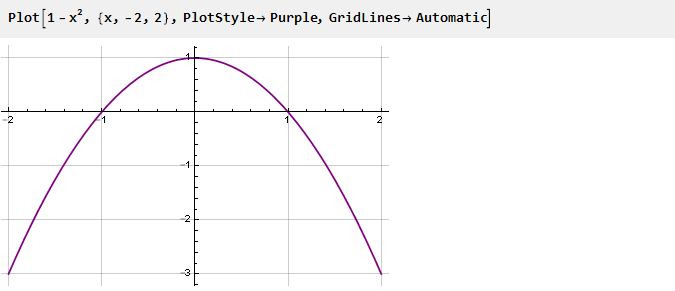
Ini akan menjadi turunan dari fungsi kami. Untuk membuatnya lebih lancar di titik-titik yang bergabung, kami akan menguadratkan, menghilangkan turunan kedua dengan cara ini:
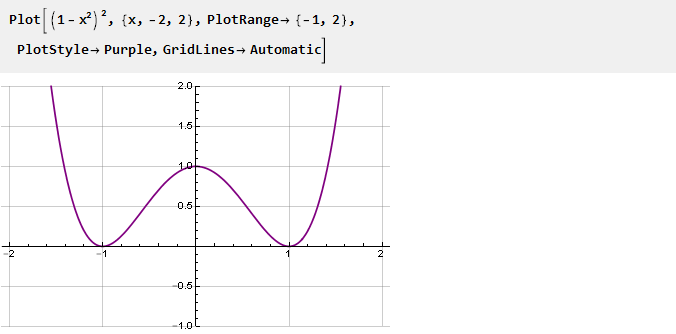
Integrasikan dan skala:

Kami mendapatkan fungsi yang lebih halus:
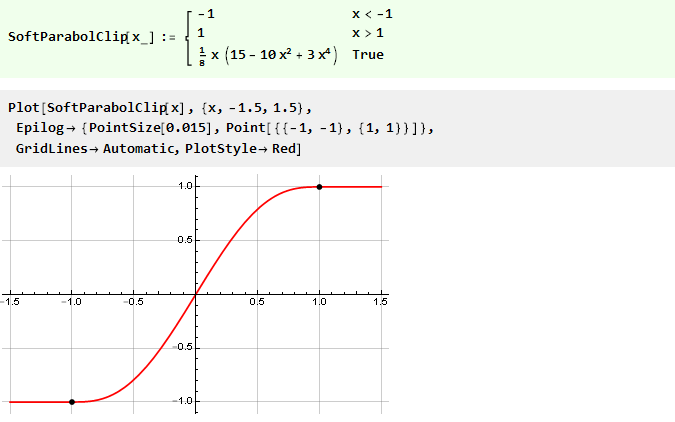
Lebih halus bagi dewa kehalusan
Di sini kami mencoba untuk mencapai kehalusan pada titik docking pada turunan yang lebih tinggi Untuk melakukan ini, sebagai permulaan, kami mendefinisikan fungsi sebagai polinomial dengan koefisien yang tidak diketahui, dan mencoba menemukan koefisien melalui solusi sistem persamaan.
Mari kita mulai dengan turunan 1:

2:

3:

Semua koefisien ini terlihat seolah-olah mereka memiliki semacam logika. Kami menulis faktor, mengalikannya dengan nilai derajat di x; dan agar tidak menulis hal yang sama setiap kali, kami mengotomatiskan proses menemukan koefisien:
 Sepertinya
Sepertinya koefisien binomial. Kami membuat asumsi yang berani bahwa mereka, dan atas dasar ini, kami menulis rumus umum:

Periksa:
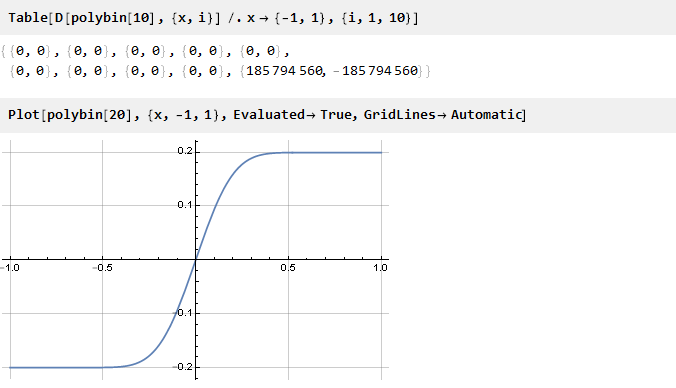
Sepertinya itu benar
[1] . Tetap hanya untuk menghitung faktor skala untuk membawa ujung menjadi satu:

Dan setelah penskalaan dan penyederhanaan, kami menemukan bahwa pengetahuan kami tentang matematika agak ketinggalan jaman
[2] :
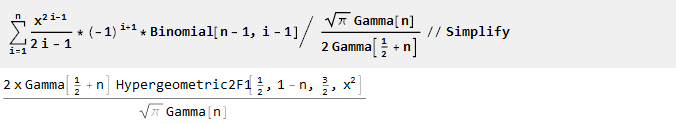
Dengan demikian, kami telah memperoleh fungsi pembangkit urutan n di mana n-1 turunan pertama sama dengan nol:

Mari kita lihat apa yang terjadi:
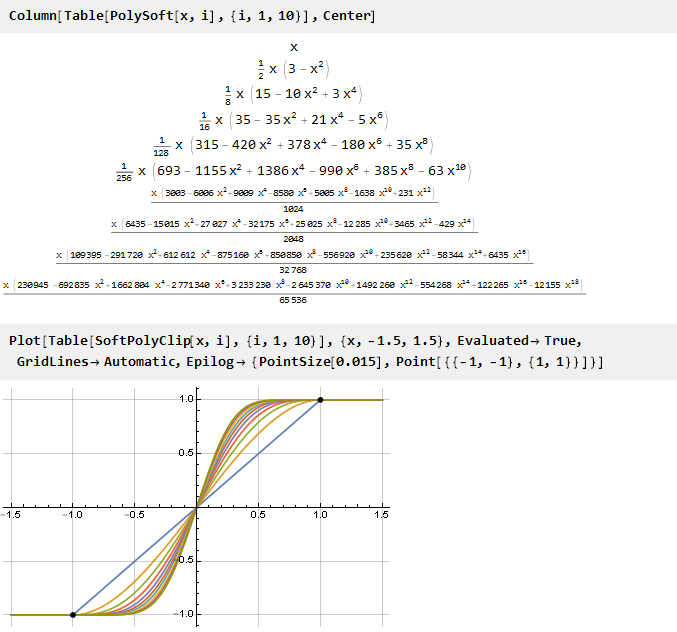
Dan karena rumus umum kami ternyata berkelanjutan, Anda dapat menggunakan nilai parameter non-integer jika Anda menginginkan:
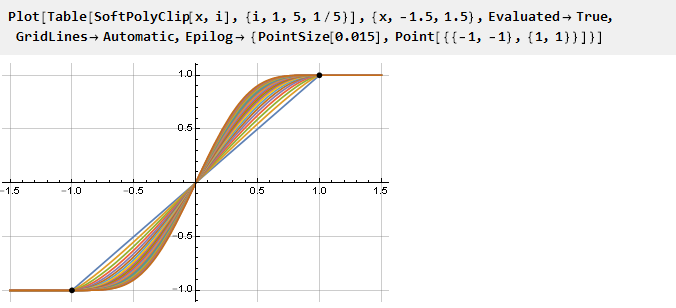
Anda juga dapat membuat grafik turunan yang dikurangi menjadi satu skala:
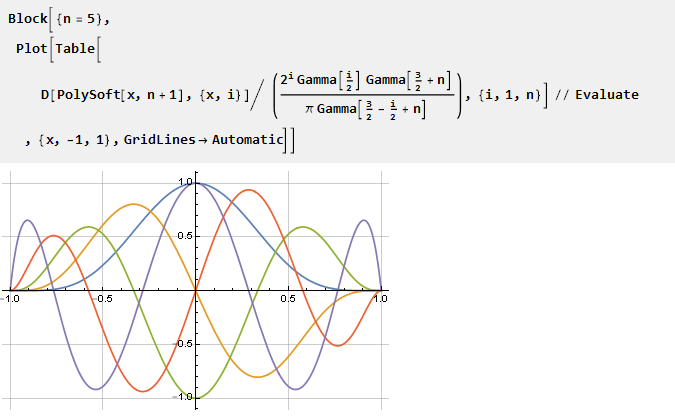
Tambahkan kekakuan
Akan menggoda untuk dapat menyesuaikan tingkat "kekakuan" pembatasan.
Mari kita kembali ke parabola terbalik kita dan menambahkan koefisien pada derajat x:

Semakin besar n, semakin besar turunannya adalah “kuadrat”, dan antiderivatifnya masing-masing tajam:
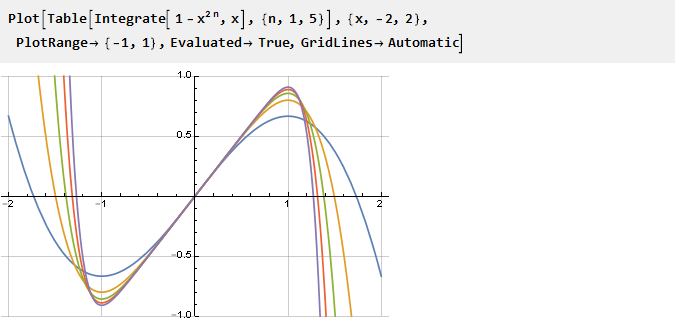
Kami menghitung antiderivatif dan menyesuaikan skala:

Sekarang mari kita coba atur langkah fraksional untuk parameter:
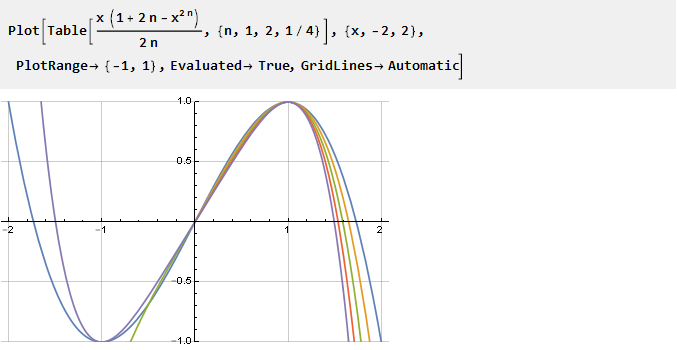
Seperti yang Anda lihat, tidak semua n memiliki solusi yang benar di bagian negatif, tetapi kondisi yang diperlukan bagi kita masih terpenuhi di bagian kanan (positif) - oleh karena itu, untuk nilai negatif kita cukup menggunakannya terbalik dengan argumen terbalik. Dan karena domain definisi parameter tidak lagi terbatas hanya pada bilangan bulat positif, kita dapat menyederhanakan rumus dengan mengganti 2n dengan n:

Dan mengganti n dengan n-1, Anda bisa membuat formula sedikit lebih indah:
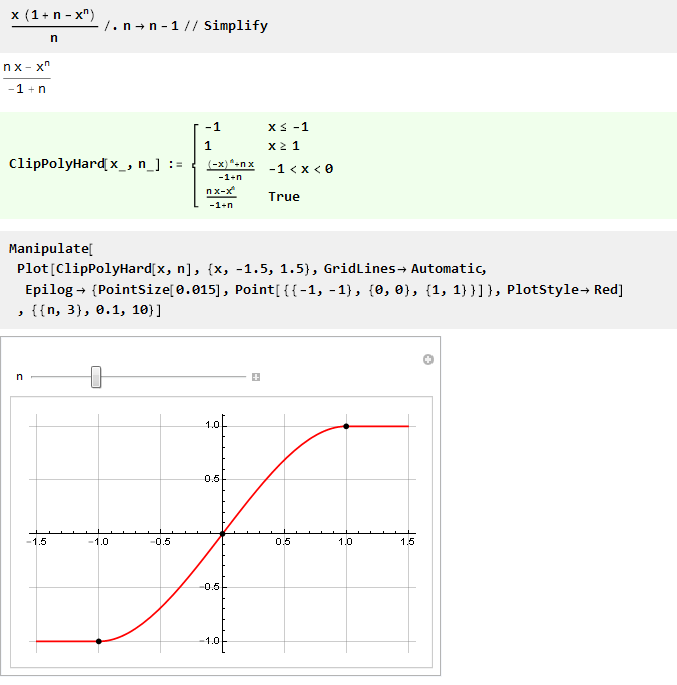
Karena untuk n sama dengan yang kita dapatkan pembagian dengan nol, maka cobalah untuk menemukan batas:

Batas ditemukan, yang berarti bahwa sekarang kita dapat menambahkan
[3] fungsi untuk n ke 1 dan mempertimbangkannya untuk semua n nol besar:
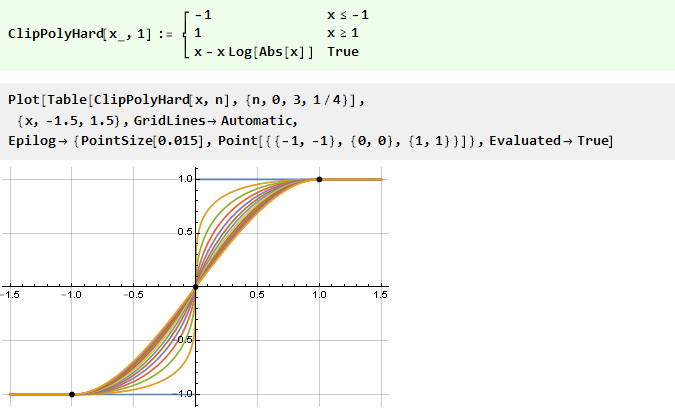
Jika awalnya kami menguak parabola terbalik kami, kami mendapatkan fungsi yang lebih halus:
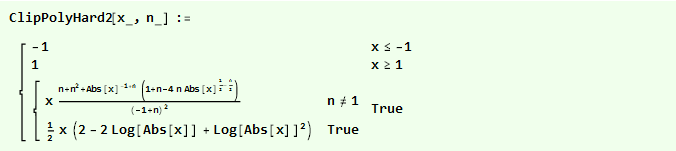
Dan kita dapat membandingkannya pada satu grafik:
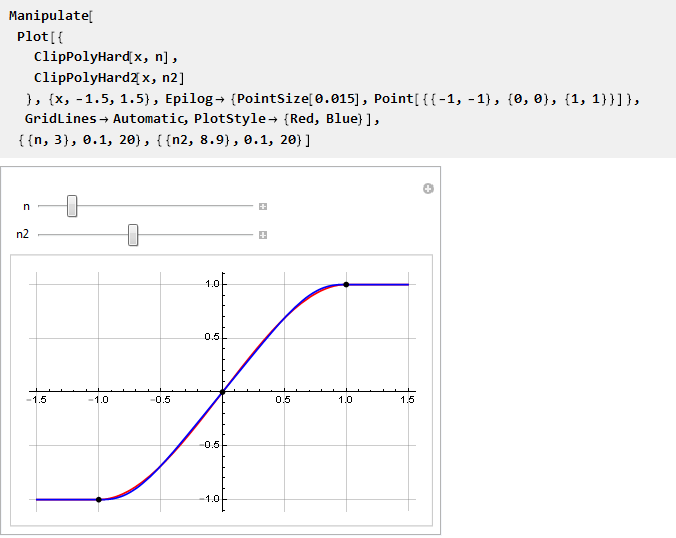
Rampingkan itu
Mari kita lihat fungsi berikut:
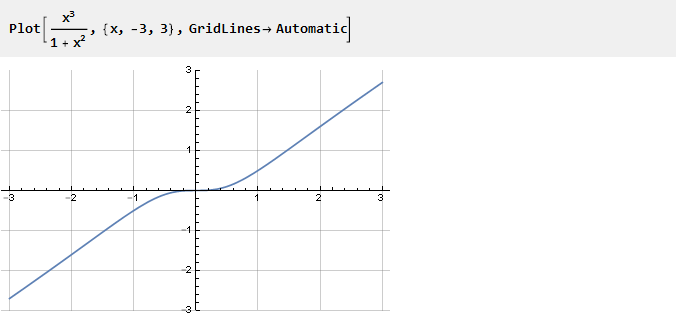
Dia muncul bukan karena kebetulan.
Jika Anda menghapus unit dari itu, x
2 akan berkontraksi dan hanya x akan tetap, yaitu garis miring. Dengan demikian, semakin kecil nilai x, semakin besar pengaruh unit dalam penyebut, menciptakan kelengkungan yang kita butuhkan. Dan mengingat fungsi ini pada skala yang berbeda, Anda dapat mengontrol tingkat kelengkungan ini:

Jadi, kita dapat menulis ulang fungsi sebelumnya dengan kontrol kekakuan hanya menggunakan polinomial 3-urutan yang rasional:
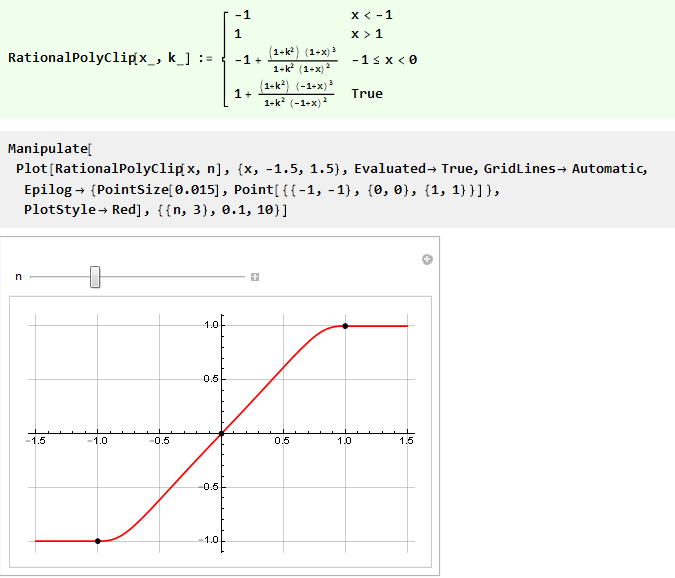
Otomatiskan itu
Agar tidak menentukan fungsi piecewise-continuous setiap kali, kita dapat mendefinisikan fungsi bantu yang akan melakukan ini sendiri, menggunakan fungsi donor sebagai argumen sebagai input.
Jika fungsi kita sudah memiliki simetri diagonal dan disejajarkan dengan pusat koordinat (seperti gelombang sinus), maka kita cukup melakukan
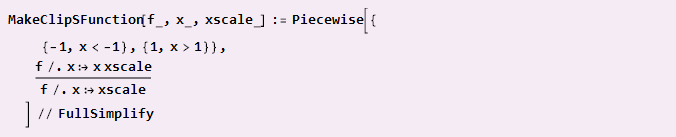
Contoh penggunaan:

Jika Anda perlu mengumpulkan dari potongan-potongan, seperti dalam kasus parabola, dan pusat koordinat menentukan titik docking, rumusnya akan sedikit lebih rumit:
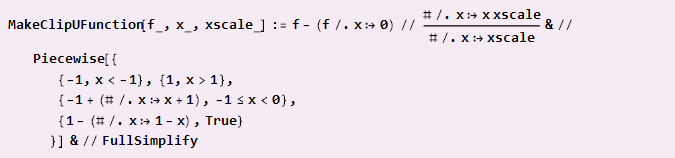
Contoh penggunaan:

Mari kita beralih ke peserta pameran
Benar-benar fungsi apa pun bisa menjadi donor untuk memecahkan masalah ini, Anda hanya perlu menyediakannya dengan titik belok. Ambil, misalnya, eksponen digeser ke bawah oleh satu:
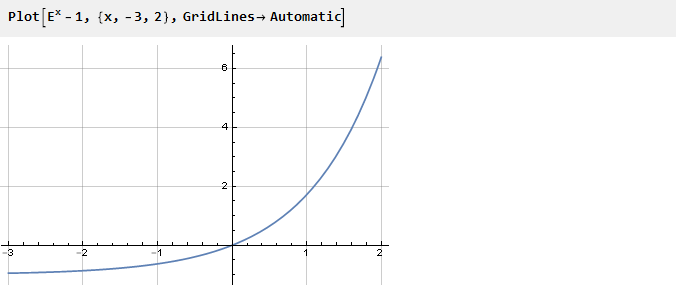
Sebelumnya, untuk memastikan infleksi yang diperlukan pada titik nol, kami mengkuadratkan fungsinya. Tapi Anda bisa pergi ke arah lain - misalnya, meringkas dengan fungsi lain yang turunannya pada titik nol bertanda berlawanan dari turunan eksponen. Misalnya, -x:
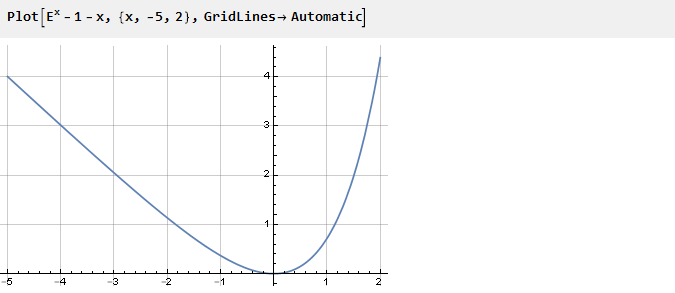
Bergantung pada sisi mana kita akan mengambil kurva, bentuk akhir dari fungsi akan bergantung padanya. Sekarang, menggunakan fungsi bantu yang didefinisikan sebelumnya dan memilih salah satu sisi, kita mendapatkan:

Baik

Dan sekarang kita bisa membandingkannya dalam satu grafik:
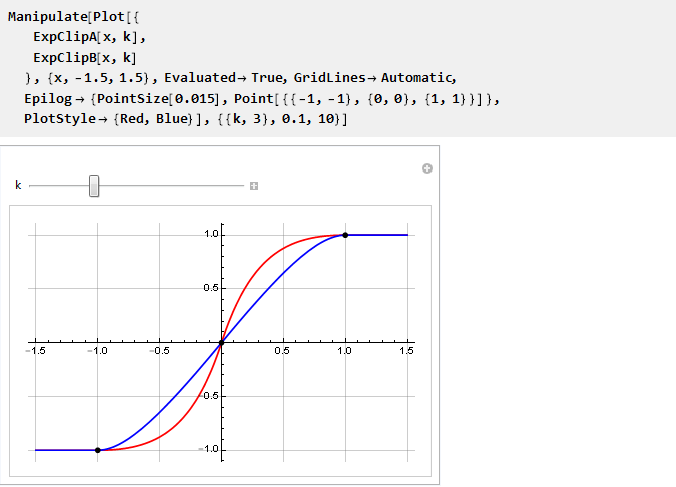
Terlihat bahwa k → 0 mereka cenderung bertepatan; dan karena kami tidak dapat secara langsung menghitung nilainya, karena kami mendapatkan pembagian dengan nol, kami akan menggunakan batas:

Dan mereka mendapatkan fungsi sambungan dari parabola yang sudah kita kenal.
Simetri putus
Sejauh ini, kami telah mempertimbangkan fungsi simetris secara eksklusif. Namun, ada kalanya kita tidak perlu simetri - misalnya, untuk mensimulasikan distorsi dalam suara amplifier tabung.
Ambil eksponen dan kalikan dengan parabola terbalik kuadrat - untuk mendapatkan persimpangan dengan sumbu absis pada titik -1 dan 1, dan pada saat yang sama memastikan kelancaran turunan kedua; parameterisasi dimungkinkan melalui penskalaan argumen eksponen:
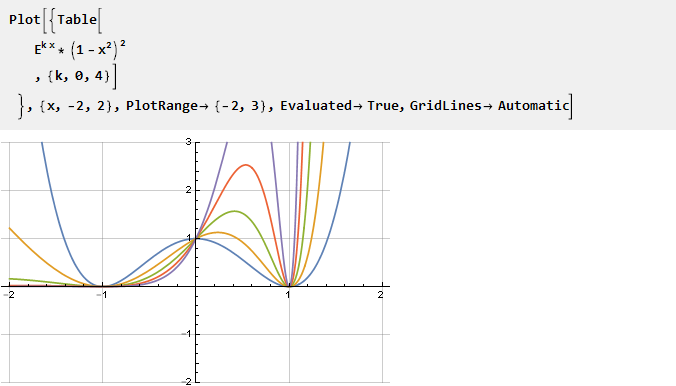
Temukan antiderivatif dan skala:
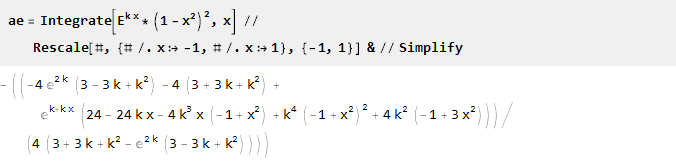
Karena untuk k = 0 kita mendapatkan pembagian dengan nol:

Kemudian kita juga menemukan batasnya,

yang merupakan polinomial halus dari urutan ketiga yang sudah kita ketahui. Menggabungkan semuanya menjadi satu fungsi, kita dapatkan
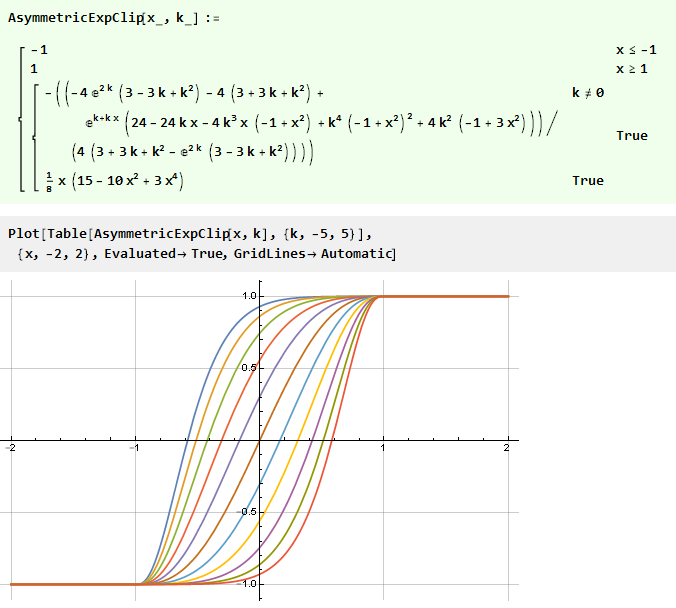
Alih-alih awalnya merancang fungsi asimetris, Anda dapat pergi ke arah lain - gunakan simetris yang sudah jadi, tetapi “tekuk” nilai fungsi ini menggunakan fungsi kurva tambahan yang ditentukan pada interval {-1,1}.
Pertimbangkan, misalnya, hiperbola:
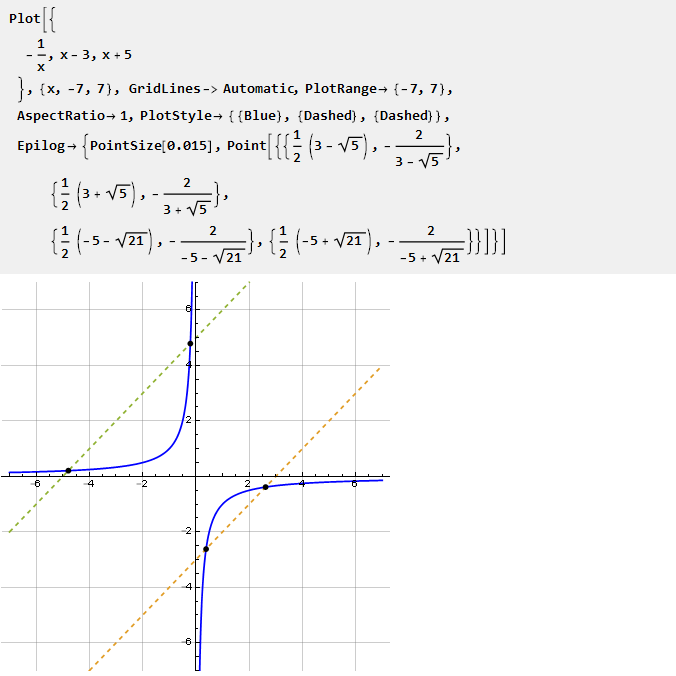
Mengingat segmennya pada skala yang berbeda, Anda dapat menyesuaikan tingkat kelengkungan di kedua arah. Bagaimana cara menemukan segmen ini? Berdasarkan grafik, orang bisa mencari persimpangan hiperbola dengan garis. Namun, karena persimpangan seperti itu tidak selalu ada, ini menciptakan beberapa kesulitan. Karena itu, kita akan pergi ke arah lain.
Pertama, tambahkan faktor penskalaan ke hiperbola:

maka kita akan menyusun sistem persamaan yang mendefinisikan kondisi untuk lewatnya hiperbola melalui poin-poin yang diberikan - dan solusinya akan memberikan koefisien yang menarik bagi kita:

Sekarang gantikan solusi dalam formula asli dan sederhanakan:

Mari kita lihat apa yang kita dapatkan, tergantung pada parameter k:
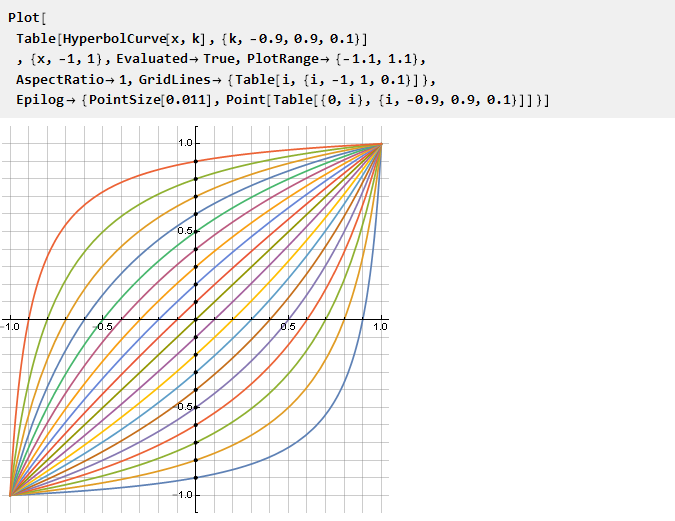
Patut dicatat bahwa untuk k = 0 formula secara alami akan runtuh pada x dan tidak ada situasi khusus yang terjadi - walaupun dengan mengacu pada hiperbola awal ini setara dengan segmen dengan panjang nol, dan dua sekaligus. Tidak kalah luar biasa bahwa fungsi yang dibaliknya sama, tetapi dengan parameter negatif k:

Sekarang kita dapat menggunakannya untuk memodifikasi fungsi kendala sembarang, dan parameter k dengan demikian menetapkan titik persimpangan dengan sumbu ordinasi:
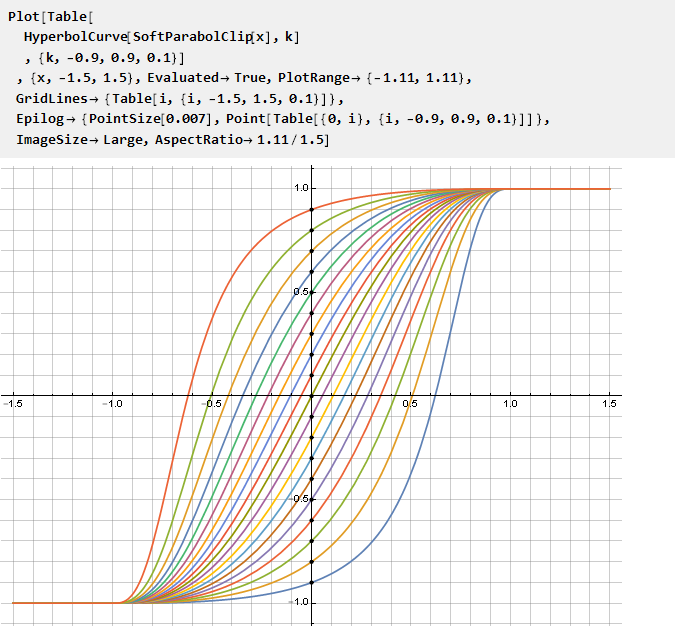
Demikian pula, Anda bisa membuat kurva dari fungsi lain, misalnya, hukum daya dengan basis variabel:
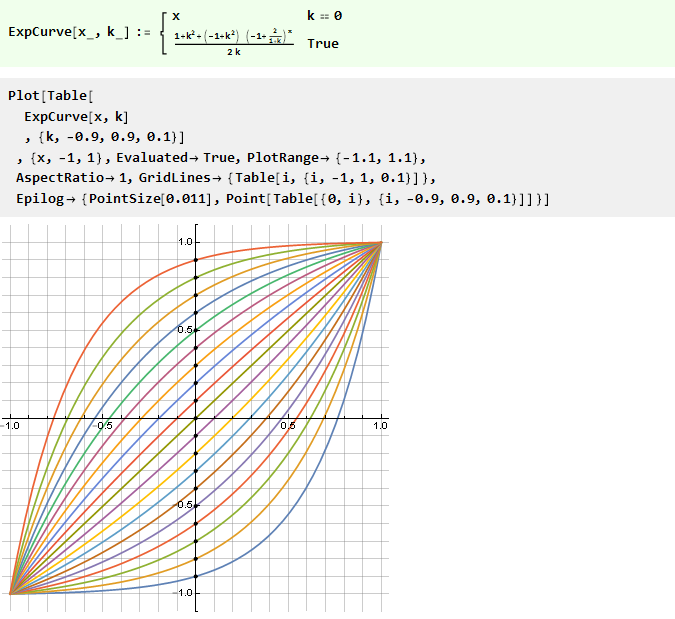
Atau kebalikannya adalah logaritmik:
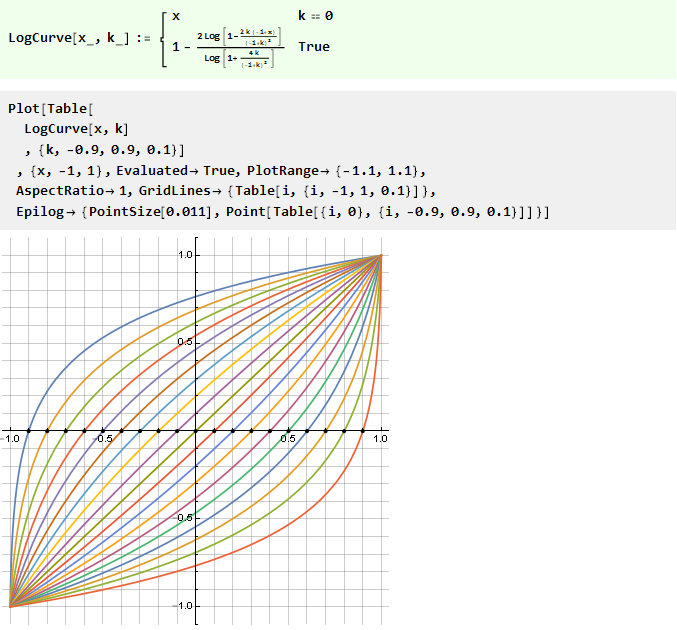
Perlu lebih akurat
Kami mungkin ingin memiliki spasi linear yang dijamin untuk suatu fungsi pada interval tertentu. Ini logis untuk mengatur dengan memperkenalkan garis lurus ke fungsi kontinyu,
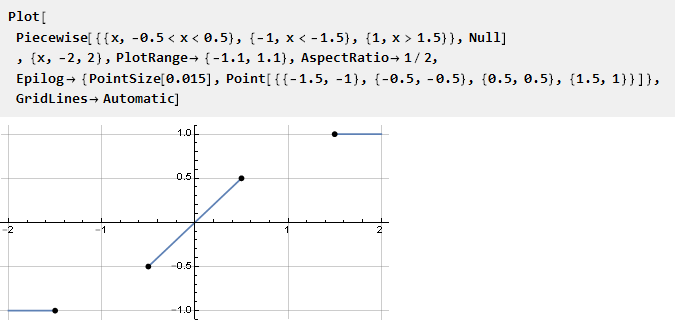
ruang kosong di mana Anda perlu mengisi beberapa fungsi. Jelas, untuk docking yang mulus dengan bagian linier, turunan pertamanya harus sama dengan persatuan; dan semua nol berikutnya (jika mungkin). Agar tidak menyimpulkan fungsi seperti itu lagi, kita dapat mengambil yang sudah jadi dan menyesuaikannya untuk tugas ini. Anda juga dapat memperhatikan bahwa titik-titik ekstrem terletak sedikit lebih jauh dari satu - ini diperlukan untuk menjaga kemiringan bagian linear.
Ambil fungsi PolySoft yang diturunkan sebelumnya dan geser sehingga kami mendapatkannya di pusat koordinat:
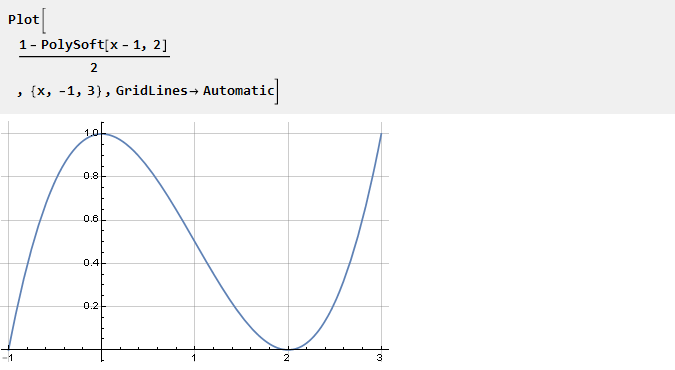
Dari sifat-sifatnya maka n-1 dari turunan berikutnya pada titik 0 dan 2 akan sama dengan nol:
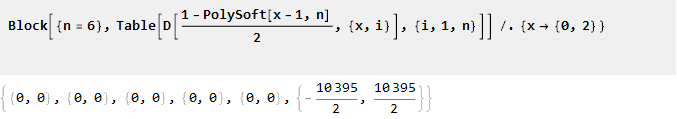
Sekarang integrasikan:
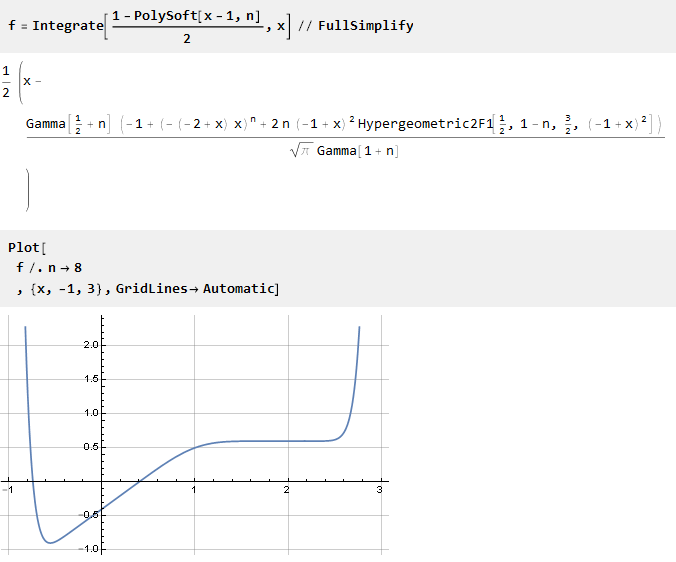
Fungsi itu bergeser ke bawah relatif terhadap sumbu absis. Oleh karena itu, perlu menambahkan konstanta (sama dengan nilai fungsi pada titik 0) untuk menggabungkan pusat koordinat:

Di sini kita memiliki nol dalam derajat n. Itu belum menurun, karena nilai nol dalam derajat nol tidak didefinisikan; kita dapat menghapusnya secara manual, atau, dalam penyederhanaan, kita dapat secara eksplisit menunjukkan bahwa n lebih besar dari nol:

Kami akan memeriksa untuk berjaga-jaga. Nilai pada poin 0 dan 2 untuk semua n:

Derivatif di tepi interval (untuk polinomial urutan 5):

Seperti yang Anda lihat, fungsinya ternyata agak rumit. Agar tidak menyeret dan tidak mempersulit perhitungan, kami akan terus memanipulasi dengan polinomial tertentu, misalnya, urutan ke-4:

Dan sekarang dengan itu Anda dapat mengisi ruang kosong:

Periksa:
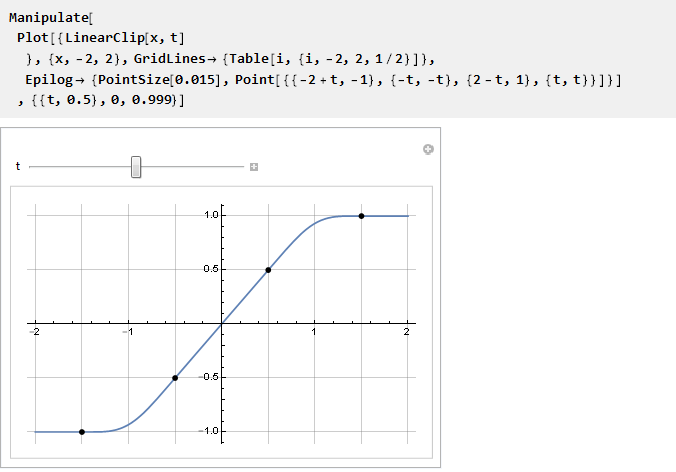
Kami pergi hingga tak terbatas
Terkadang mungkin ada kebutuhan untuk fungsi yang cenderung ke suatu unit tetapi tidak mencapainya. Wikipedia
menyarankan beberapa solusi terkenal:
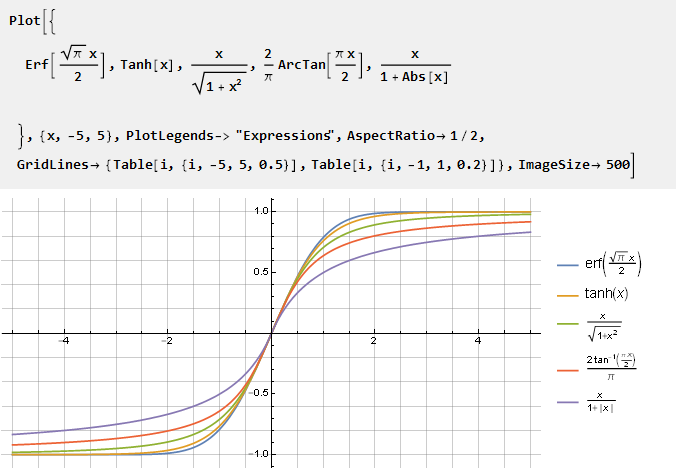
Karena fungsi-fungsi ini tidak mencapai kesatuan, lebih mudah untuk menormalkannya sehubungan dengan turunannya di pusat koordinat.
Kita dapat memodifikasi bentuk fungsi tersebut melalui argumennya menggunakan beberapa fungsi diagonal-simetris, misalnya:
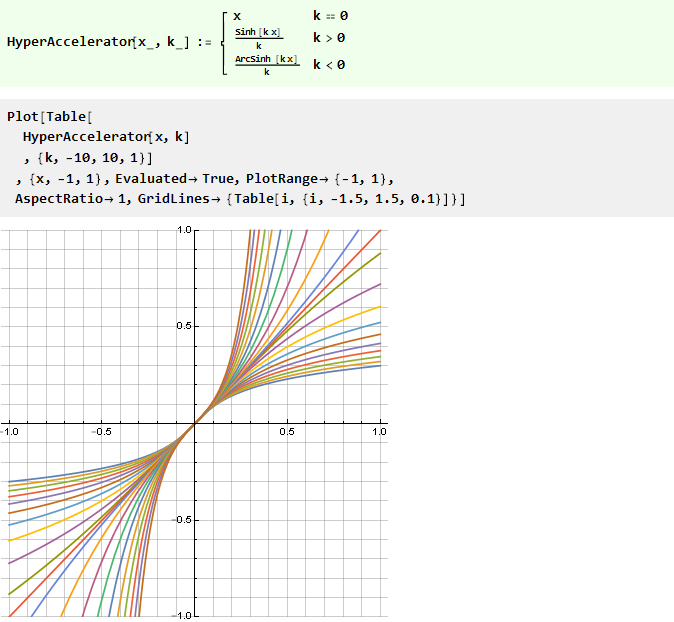
Fungsi ini, omong-omong, juga terbalik dengan dirinya sendiri, yaitu
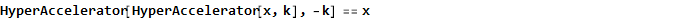
Dan, sebagaimana diterapkan pada arctangent, sebagai contoh, kita dapatkan
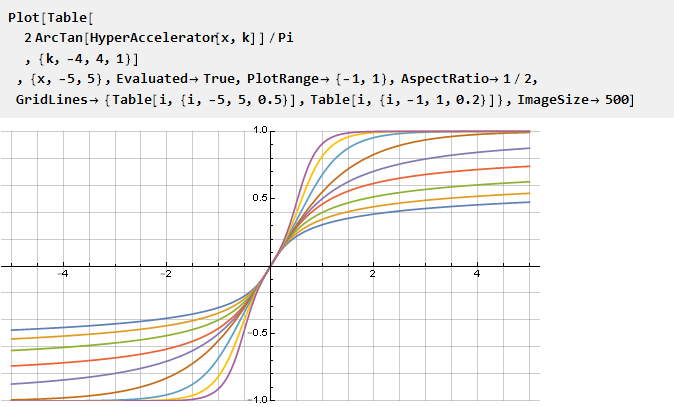
yang, khususnya, dengan parameter k = 1 akan memberi kita
fungsi Guderman .
Seperti yang Anda lihat, dengan pendekatan ini, ketegaran yang tidak diinginkan dapat diperoleh, oleh karena itu lebih disukai untuk mengontrol kekakuan kendala secara langsung melalui properti fungsi itu sendiri. Pertimbangkan beberapa fungsi dengan parameter, yang hasilnya dihilangkan untuk singkatnya.
Dari fungsi daya:
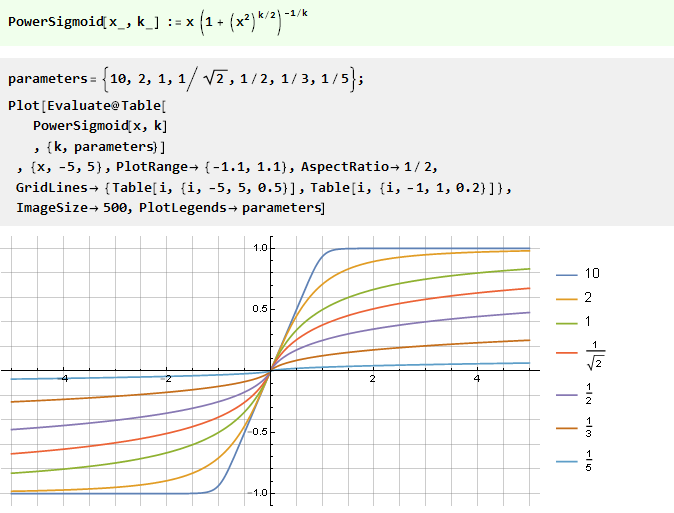
Dari jumlah dua fungsi berbentuk-v dengan offset:
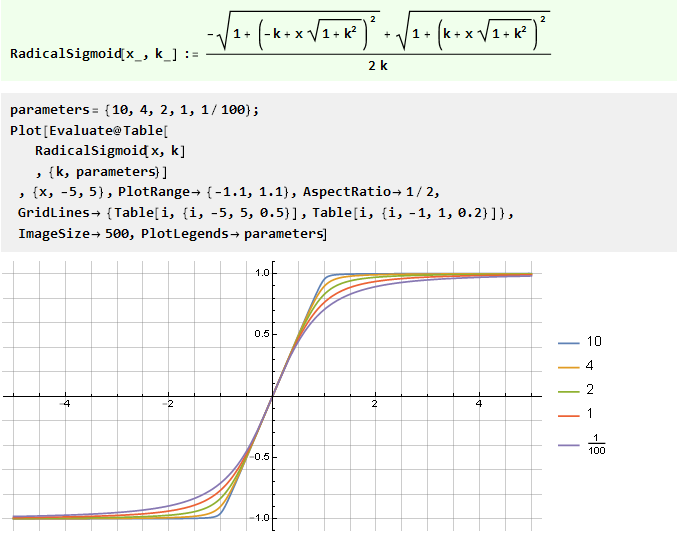
Dari fungsi kesalahan umum:
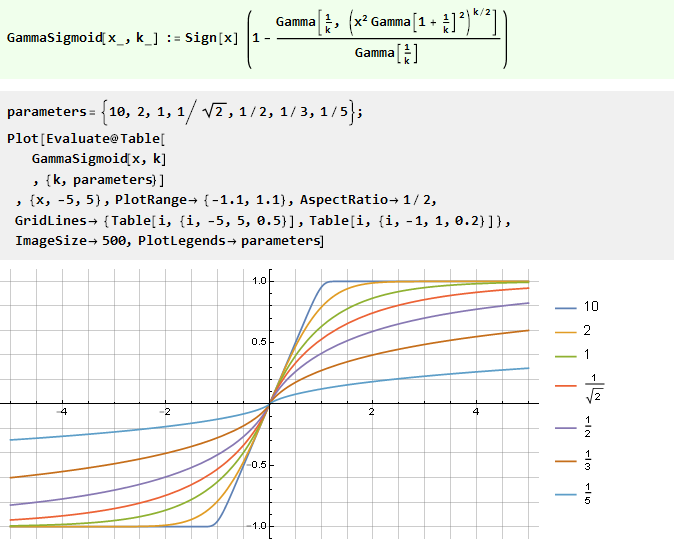
Integrasi polinomial rasional:
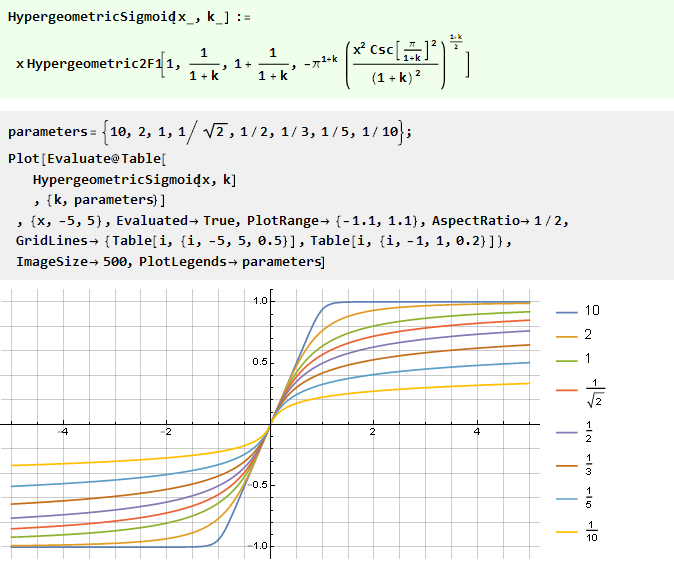
Menariknya, kasus khususnya adalah arctangent:

Kesimpulan
Konstruksi fungsi semacam itu bisa menjadi kegiatan yang menarik, di mana formula sederhana dan kompleks, indah dan tidak terlalu, akan diperoleh. Tampaknya mereka semua sangat mirip satu sama lain dan tidak perlu untuk varietas seperti itu. Ini belum tentu demikian.
Perbedaannya bisa lebih terlihat pada skala lain - misalnya, logaritmik. Selain itu, di samping tugas-tugas yang ditunjukkan dalam header, fungsi serupa dapat digunakan dalam tugas-tugas lain - pencampuran sinyal, ketika pelemahan halus dari satu sinyal dikombinasikan dengan peningkatan halus dari yang lain, atau pembangunan filter akustik - dan kemudian perbedaan akan dirasakan oleh telinga, atau untuk membangun gradien - dan kemudian perbedaan akan dirasakan oleh mata. Selain itu, mereka juga dapat digunakan sebagai donor untuk fungsi lain yang lebih kompleks - misalnya
jendela .
Sebagai kesimpulan, ada baiknya mengklarifikasi beberapa poin lagi.
Semua fungsi di sini didefinisikan dalam rentang dari -1 hingga 1. Jika Anda memerlukan rentang yang berbeda (misalnya, dari 0 hingga 1), dapat dengan mudah dihitung ulang secara manual:
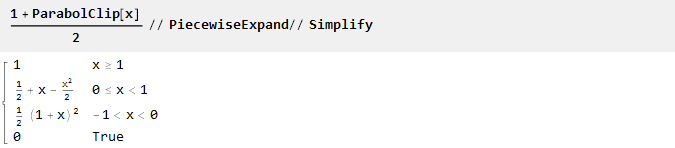
Atau menggunakan fungsi zoom bawaan:

Dan untuk memfasilitasi ekspor formula yang diperoleh ke kode program, fungsi CForm mungkin berguna:
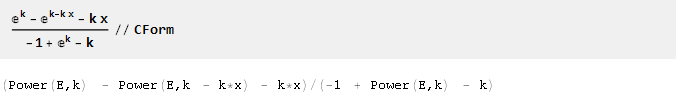
Dokumen sumber Mathematica dapat diunduh di
sini .
Catatan:
[1] Matematikawan sejati pasti dapat membuktikan (atau menyangkal) pernyataan ini dengan seksama.
[2] fungsi hypergeometrik tidak dipertimbangkan dalam kursus standar analisis matematika.
[3] kelebihan ini hanya ditentukan untuk unit karakter; sebuah unit dalam format floating point (misalnya, ketika merencanakan grafik) tidak akan dikenali.