Hai habr.
Tema "kotak ajaib" cukup menarik, karena di satu sisi, mereka telah dikenal sejak jaman dahulu, di sisi lain, perhitungan "kotak ajaib" bahkan hari ini adalah tugas komputasi yang sangat sulit. Ingatlah bahwa untuk membangun "kotak ajaib" NxN, Anda harus memasukkan angka 1..N * N sehingga jumlah horizontalnya, vertikal dan diagonal sama dengan angka yang sama. Jika Anda cukup memilah-milah jumlah semua opsi untuk mengatur angka-angka untuk kuadrat 4x4, kami mendapatkan 16! = 20.922.789.888.000 opsi.
Pertimbangkan bagaimana ini dapat dilakukan dengan lebih efisien.

Untuk mulai dengan, kami mengulangi kondisi masalah. Anda perlu mengatur angka dalam kotak sehingga tidak mengulangi, dan jumlah kontur, vertikal dan diagonal sama dengan angka yang sama.
Mudah untuk membuktikan bahwa jumlah ini selalu sama, dan dihitung dengan rumus untuk setiap n:
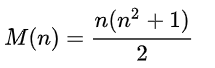
Kami akan mempertimbangkan kotak 4x4, jadi jumlahnya = 34.
Lambangkan semua variabel dengan X, kuadrat kita akan terlihat seperti ini:
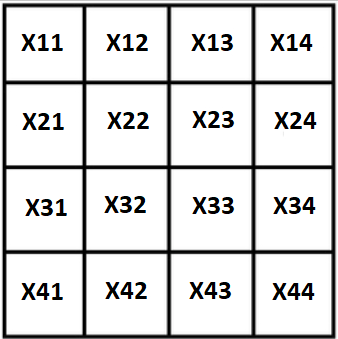
Properti pertama, dan jelas: jumlah kuadrat diketahui, gerobak ekstrem dapat diekspresikan melalui 3 sisanya:
X14 = S - X11 - X12 - X13
X24 = S - X21 - X22 - X23
...
X41 = S - X11 - X21 - X31Dengan demikian, kotak 4x4 sebenarnya berubah menjadi kotak 3x3, yang mengurangi jumlah opsi pencarian dari 16! hingga 9 !, mis. 57 juta kali. Mengetahui hal ini, kita mulai menulis kode, melihat betapa rumitnya pencarian yang melelahkan untuk komputer modern.
C ++ - versi berulir tunggal
Prinsip program ini sangat sederhana. Kami mengambil set angka 1..16 dan untuk loop atas set ini, itu akan menjadi x11. Kemudian kita mengambil set kedua, terdiri dari yang pertama dengan pengecualian angka x11, dan seterusnya.
Perkiraan bentuk program terlihat seperti ini:
int squares = 0; int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); for (int x11 = 1; x11 <= MAX; x11++) { Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; ... int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue;
Teks lengkap program dapat ditemukan di bawah spoiler.
Seluruh Sumber #include <set> #include <stdio.h> #include <ctime> #include "stdafx.h" typedef std::set<int> Set; typedef Set::iterator SetIterator; #define N 4 #define MAX (N*N) #define S 34 int main(int argc, char *argv[]) { // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 const clock_t begin_time = clock(); int squares = 0; int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); for (int x11 = 1; x11 <= MAX; x11++) { Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; Set set21(set13); set21.erase(x13); set21.erase(x14); for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) { int x21 = *it21; Set set22(set21); set22.erase(x21); for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) { int x22 = *it22; Set set23(set22); set23.erase(x22); for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) { int x23 = *it23, x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; Set set31(set23); set31.erase(x23); set31.erase(x24); for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) { int x31 = *it31; Set set32(set31); set32.erase(x31); for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) { int x32 = *it32; Set set33(set32); set33.erase(x32); for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) { int x33 = *it33, x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } } } } } } } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; }
Hasil: total
7040 4x4 "kotak ajaib" ditemukan, dan waktu pencarian adalah
102-an .

Ngomong-ngomong, menarik untuk memeriksa apakah daftar kotak berisi yang sama yang digambarkan pada ukiran Durer. Tentu saja ada, karena program menampilkan
semua kotak 4x4:
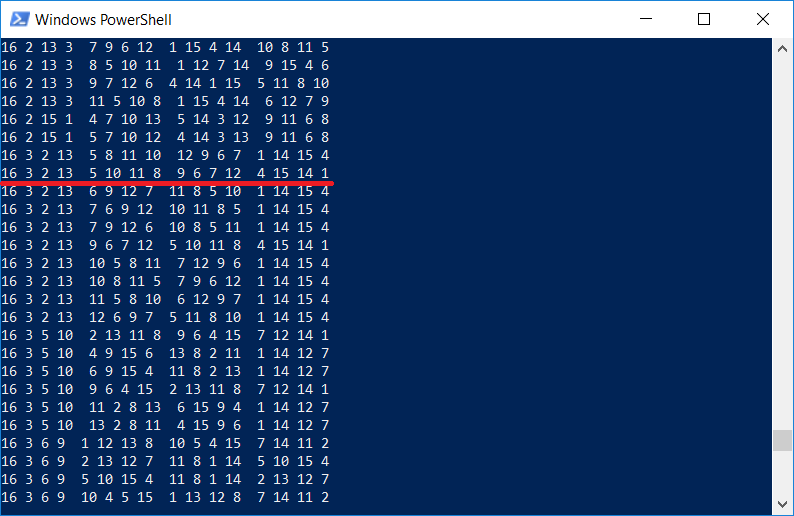
Perlu dicatat bahwa Dürer memasukkan persegi ke dalam gambar karena suatu alasan, angka
1514 juga menunjukkan tahun ukiran.
Seperti yang Anda lihat, program ini berfungsi (kami menandai tugas yang diverifikasi pada 1514 oleh Albrecht Dürer;), namun, waktu eksekusi tidak terlalu kecil untuk komputer dengan prosesor Core i7. Jelas, program berjalan dalam satu utas, dan disarankan untuk menggunakan semua kernel lainnya.
C ++ - versi multi-utas
Menulis ulang sebuah program menggunakan stream pada dasarnya mudah, meskipun agak rumit. Untungnya, ada opsi yang hampir dilupakan saat ini - penggunaan dukungan untuk
OpenMP (Open Multi-Processing). Teknologi ini telah ada sejak tahun 1998, dan memungkinkan arahan prosesor untuk memberitahu kompiler bagian mana dari program untuk berjalan secara paralel. OpenMP juga didukung di Visual Studio, jadi untuk mengubah program menjadi multi-utas, cukup tambahkan satu baris ke kode:
int squares = 0; #pragma omp parallel for reduction(+: squares) for (int x11 = 1; x11 <= MAX; x11++) { ... } printf("CNT: %d\n", squares);
Arahan #pragma omp parallel untuk menunjukkan bahwa loop berikutnya untuk dapat dieksekusi secara paralel, dan kotak parameter tambahan menetapkan nama variabel, yang akan umum untuk thread paralel (tanpa ini, kenaikan tidak berfungsi dengan benar).
Hasilnya jelas: waktu eksekusi telah dikurangi dari 102 menjadi
18-an .

Seluruh Sumber #include <set> #include <stdio.h> #include <ctime> #include "stdafx.h" typedef std::set<int> Set; typedef Set::iterator SetIterator; #define N 4 #define MAX (N*N) #define S 34 int main(int argc, char *argv[]) { // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 const clock_t begin_time = clock(); int squares = 0; #pragma omp parallel for reduction(+: squares) for (int x11 = 1; x11 <= MAX; x11++) { int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; Set set21(set13); set21.erase(x13); set21.erase(x14); for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) { int x21 = *it21; Set set22(set21); set22.erase(x21); for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) { int x22 = *it22; Set set23(set22); set23.erase(x22); for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) { int x23 = *it23, x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; Set set31(set23); set31.erase(x23); set31.erase(x24); for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) { int x31 = *it31; Set set32(set31); set32.erase(x31); for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) { int x32 = *it32; Set set33(set32); set33.erase(x32); for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) { int x33 = *it33, x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } } } } } } } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; }
Ini jauh lebih baik - karena tugasnya hampir sempurna diparalelkan (perhitungan di masing-masing cabang independen satu sama lain), waktu kurang dari jumlah kali sama dengan jumlah inti prosesor. Namun sayangnya, tidak mungkin mendapatkan lebih banyak dari kode ini, meskipun beberapa persen dapat dan dapat dimenangkan oleh beberapa optimasi. Kami lolos ke artileri yang lebih berat, perhitungan pada GPU.
Komputasi dengan NVIDIA CUDA
Jika Anda tidak merinci, maka proses perhitungan yang dilakukan pada kartu video dapat direpresentasikan sebagai beberapa blok perangkat keras paralel (blok), yang masing-masing melakukan beberapa proses (utas).
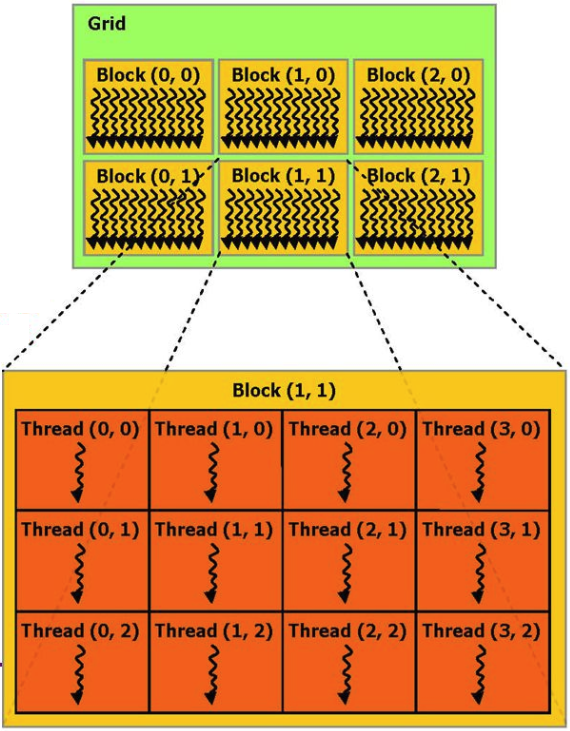
Sebagai contoh, kita dapat memberikan contoh fungsi menambahkan 2 vektor dari dokumentasi CUDA:
__global__ void add(int n, float *x, float *y) { int index = threadIdx.x; int stride = blockDim.x; for (int i = index; i < n; i += stride) y[i] = x[i] + y[i]; }
Array x dan y adalah umum untuk semua blok, dan fungsi itu sendiri dieksekusi secara bersamaan pada beberapa prosesor sekaligus. Kuncinya di sini adalah paralelisme - prosesor kartu video jauh lebih sederhana daripada CPU biasa, tetapi ada banyak dari mereka dan mereka berfokus khusus pada pemrosesan data numerik.
Inilah yang kami butuhkan. Kami memiliki matriks angka X11, X12, .., X44. Mari kita mulai proses 16 blok, yang masing-masing akan menjalankan 16 proses. Nomor blok akan sesuai dengan nomor X11, nomor proses ke nomor X12, dan kode itu sendiri akan menghitung semua kotak yang mungkin dengan untuk X11 dan X12 yang dipilih. Ini sederhana, tetapi ada satu kehalusan - data tidak hanya perlu dihitung, tetapi juga ditransfer dari kartu video kembali, untuk ini kami akan menyimpan jumlah kotak yang ditemukan dalam elemen nol array.
Kode utama sangat sederhana:
#define N 4 #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) int main(int argc,char *argv[]) { const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; }
Kami memilih blok memori pada kartu video menggunakan cudaMalloc, menjalankan fungsi kuadrat, menunjukkan 2 parameter 16.16 (jumlah blok dan jumlah utas) yang sesuai dengan angka 1..16 berulang, lalu menyalin data kembali melalui cudaMemcpy.
Fungsi kotak itu sendiri pada dasarnya mengulangi kode dari bagian sebelumnya, dengan perbedaan bahwa penambahan jumlah kotak yang ditemukan dilakukan menggunakan atomicAdd - ini memastikan bahwa variabel akan berubah dengan benar selama panggilan simultan.
Hasilnya tidak memerlukan komentar - waktu eksekusi adalah
2,7 detik , yang sekitar 30 kali lebih baik daripada versi single-threaded awal:

Seperti yang disarankan dalam komentar, Anda dapat menggunakan lebih banyak blok perangkat keras dari kartu video, sehingga opsi 256 blok telah dicoba. Mengubah kode minimal:
__global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX; ... } squares<<<MAX*MAX, 1>>>(gpu_out);
Ini mengurangi waktu sebanyak 2 kali, menjadi
1,2 detik . Selanjutnya, pada setiap blok, 16 proses dapat dimulai, yang memberikan waktu terbaik
0,44 .
Kode akhir #include <stdio.h> #include <ctime> #define N 4 #define MAX (N*N) #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) #define S 34 // Magic square: // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 __global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX, index3 = threadIdx.x; if (index1 + 1 > MAX || index2 + 1 > MAX || index3 + 1 > MAX) return; const int x11 = index1+1, x12 = index2+1, x13 = index3+1; if (x13 == x11 || x13 == x12) return; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) return; if (x14 == x11 || x14 == x12 || x14 == x13) return; for(int x21=1; x21<=MAX; x21++) { if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14) continue; for(int x22=1; x22<=MAX; x22++) { if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21) continue; for(int x23=1; x23<=MAX; x23++) { int x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; for(int x31=1; x31<=MAX; x31++) { if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 || x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24) continue; for(int x32=1; x32<=MAX; x32++) { if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31) continue; for(int x33=1; x33<=MAX; x33++) { int x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; const int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; // Square found: save in array (MAX numbers for each square) int p = atomicAdd(res_array, 1); if (p >= SQ_MAX) continue; int i = MAX*p + 1; res_array[i] = x11; res_array[i+1] = x12; res_array[i+2] = x13; res_array[i+3] = x14; res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6] = x23; res_array[i+7] = x24; res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34; res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44; // Warning: printf from kernel makes calculation 2-3x slower // printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); } } } } } } } int main(int argc,char *argv[]) { int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX*MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; }
Kemungkinan besar, ini jauh dari ideal, misalnya, Anda dapat menjalankan lebih banyak blok pada GPU, tetapi ini akan membuat kode lebih membingungkan dan sulit dipahami. Dan tentu saja, perhitungannya tidak "gratis" - ketika GPU dimuat, antarmuka Windows mulai melambat secara nyata, dan konsumsi daya komputer hampir dua kali lipat, dari 65 menjadi 130W.
Sunting : ketika pengguna
Bodigrim diminta dalam komentar, kesetaraan lain berlaku untuk kuadrat 4x4: jumlah 4 sel "internal" sama dengan jumlah yang "eksternal", itu juga S.

X22 + X23 + X32 + X33 = X11 + X41 + X14 + X44 = SIni akan memungkinkan untuk mempercepat algoritma dengan mengekspresikan beberapa variabel melalui yang lain dan menghapus 1-2 loop bersarang lainnya, versi terbaru dari kode dapat ditemukan dalam komentar di bawah ini.Kesimpulan
Tugas menemukan "kotak ajaib" ternyata secara teknis sangat menarik, dan pada saat yang sama sulit. Bahkan dengan perhitungan pada GPU, pencarian semua kotak 5x5 dapat memakan waktu beberapa jam, dan optimasi untuk menemukan kotak ajaib 7x7 dan dimensi yang lebih tinggi masih harus dilakukan.Secara matematis dan algoritmik, ada juga beberapa masalah yang belum terselesaikan:- « » N. 22 , 33 8 ( 1, ), 44 , 7040, . .
- , .
- . , NVIDIA Tesla , - , . , . , ;)
Artikel terpisah dapat ditulis tentang analisis dan properti kotak ajaib itu sendiri, jika ada minat.PS: Untuk pertanyaan yang kemungkinan akan mengikuti, "mengapa ini perlu." Dalam hal konsumsi daya, menghitung kotak ajaib tidak lebih baik atau lebih buruk daripada menghitung bitcoin, jadi mengapa tidak? Selain itu, ini adalah latihan yang menarik untuk pikiran dan tugas yang menarik di bidang pemrograman terapan.