Kursus MIT "Keamanan Sistem Komputer". Kuliah 10: Eksekusi Simbolik, Bagian 3

Institut Teknologi Massachusetts. Kursus Kuliah # 6.858. "Keamanan sistem komputer." Nikolai Zeldovich, James Mickens. Tahun 2014

Keamanan Sistem Komputer adalah kursus tentang pengembangan dan implementasi sistem komputer yang aman. Ceramah mencakup model ancaman, serangan yang membahayakan keamanan, dan teknik keamanan berdasarkan pada karya ilmiah baru-baru ini. Topik meliputi keamanan sistem operasi (OS), fitur, manajemen aliran informasi, keamanan bahasa, protokol jaringan, keamanan perangkat keras, dan keamanan aplikasi web.

Kuliah 1: “Pendahuluan: model ancaman” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 2: "Kontrol serangan hacker" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 3: “Buffer Overflows: Exploits and Protection” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 4: “Pemisahan Hak Istimewa” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 5: "Dari mana sistem keamanan berasal?" Bagian 1 / Bagian 2
Kuliah 6: “Peluang” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 7: “Kotak Pasir Klien Asli” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 8: “Model Keamanan Jaringan” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 9: "Keamanan Aplikasi Web" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 10: “Eksekusi simbolik” Bagian 1 / Bagian 2 / Bagian 3

Sekarang, mengikuti cabang ke bawah, kita melihat ekspresi t = y. Karena kami mempertimbangkan satu jalur pada satu waktu, kami tidak harus memperkenalkan variabel baru untuk t. Kita dapat mengatakan bahwa karena t = y, maka t tidak lagi 0.

Kami terus bergerak ke bawah dan sampai ke titik di mana kami sampai ke cabang lain. Apa asumsi baru yang harus kita buat untuk mengikuti jalan ini lebih jauh? Ini adalah asumsi bahwa t <y.

Apa itu t? Jika Anda mencari cabang kanan, kita akan melihat bahwa t = y. Dan di tabel kami, T = y dan Y = y. Secara logis ini mengikuti dari sini bahwa pembatasan kita terlihat seperti y <y, yang tidak mungkin.



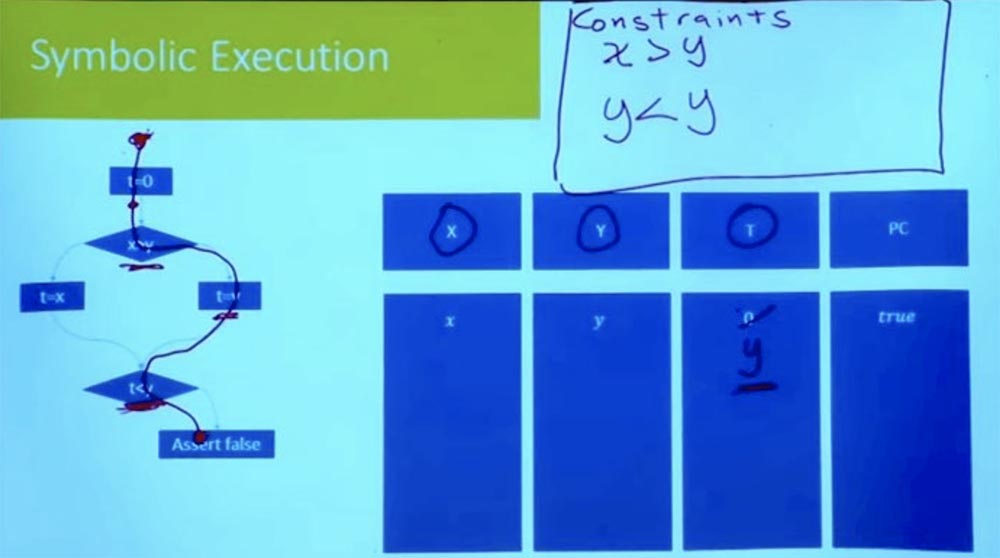
Dengan demikian, kami memiliki semuanya dalam urutan sampai kami mencapai titik ini t <y. Sampai kita sampai pada pernyataan yang salah, kita memiliki semua ketidaksetaraan untuk menjadi benar. Tapi ini tidak berhasil, karena ketika melakukan tugas-tugas cabang kanan, kami memiliki inkonsistensi logis.

Kita memiliki apa yang sering disebut kondisi sang jalan. Kondisi ini harus benar untuk program berjalan seperti ini. Tetapi kita tahu bahwa kondisi ini tidak dapat dipenuhi, oleh karena itu tidak mungkin bagi program untuk pergi seperti ini. Jadi jalan ini sekarang telah sepenuhnya dihilangkan, dan kita tahu bahwa jalan yang benar ini tidak dapat dilalui.

Bagaimana dengan sebaliknya? Mari kita coba melalui cabang kiri dengan cara yang berbeda. Apa yang akan menjadi kondisi untuk jalur ini? Sekali lagi, keadaan simbolis kita dimulai pada t = 0, dan X dan Y sama dengan variabel x dan y.



Seperti apa batasan jalan dalam kasus ini sekarang? Kami menunjukkan cabang kiri sebagai Benar, dan cabang kanan sebagai Salah dan selanjutnya mempertimbangkan nilai t = x. Sebagai hasil dari pemrosesan logis dari kondisi t = x, x> y dan t <y, kita mendapatkan bahwa kita secara bersamaan memiliki apa yang x> y dan x <y.



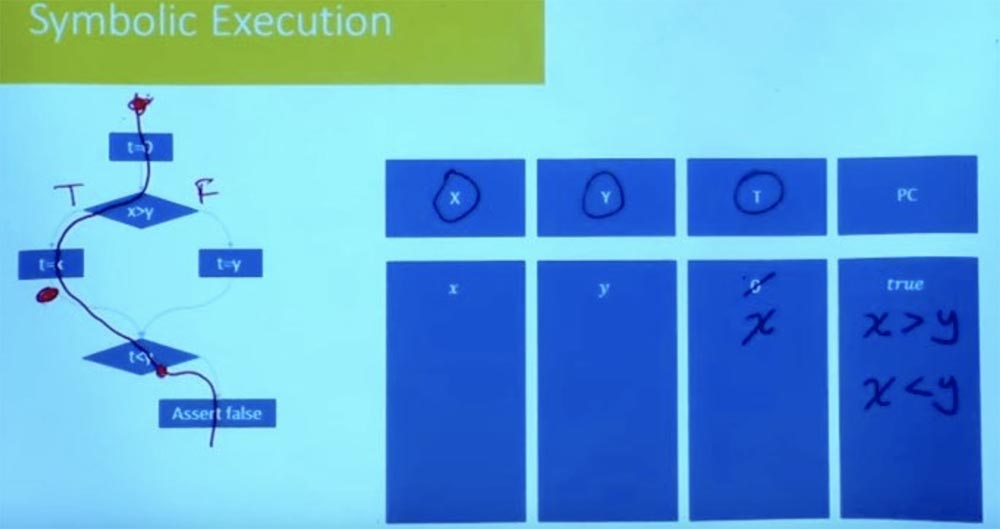
Jelas bahwa kondisi jalan ini tidak memuaskan. Kita tidak dapat memiliki x yang lebih besar dan lebih kecil dari y. Tidak ada tugas untuk variabel X yang memenuhi kedua kendala. Dengan demikian, ini memberitahu kita bahwa cara lain juga tidak memuaskan.

Ternyata pada saat ini kami menjelajahi semua jalur yang mungkin dalam program yang dapat membawa kami ke keadaan ini. Kami benar-benar dapat menetapkan dan memverifikasi bahwa tidak ada cara yang mungkin yang akan membawa kami ke pernyataan yang salah.
Hadirin: Dalam contoh ini, Anda menunjukkan bahwa Anda mempelajari kemajuan suatu program di sepanjang semua cabang yang mungkin. Tetapi salah satu keuntungan dari eksekusi simbolik adalah bahwa kita tidak perlu mempelajari semua jalur eksponensial yang mungkin. Jadi bagaimana cara menghindari ini dalam contoh ini?

Profesor: Ini pertanyaan yang sangat bagus. Dalam hal ini, Anda berkompromi antara eksekusi karakter dan seberapa spesifik Anda inginkan. Jadi dalam kasus ini, kita tidak begitu banyak menggunakan eksekusi simbolis karena pertama kali kita melihat aliran program pada kedua cabang secara bersamaan. Namun berkat ini, keterbatasan kami menjadi sangat, sangat sederhana.

Batasan individu “satu demi satu” sangat sederhana, tetapi Anda harus melakukannya berulang kali, mempelajari semua cabang yang ada, dan secara eksponensial - dan semua cara yang mungkin.
Ada banyak jalur secara eksponensial, tetapi untuk setiap jalur secara keseluruhan, ada juga sejumlah besar data input yang eksponensial yang dapat melewati jalur tersebut. Jadi ini sudah memberi Anda keuntungan besar, karena alih-alih mencoba semua input yang mungkin, Anda mencoba untuk mencoba segala cara yang mungkin. Tetapi bisakah Anda melakukan sesuatu yang lebih baik?

Ini adalah salah satu area di mana banyak percobaan telah dilakukan mengenai eksekusi simbolik, misalnya, eksekusi simultan dari beberapa jalur. Dalam materi kuliah Anda bertemu heuristik dan serangkaian strategi yang digunakan para eksperimen untuk membuat pencarian lebih dapat dipecahkan.

Sebagai contoh, salah satu hal yang mereka lakukan adalah mereka mengeksplorasi satu demi satu, tetapi tidak melakukannya secara membabi buta. Mereka memeriksa kondisi jalan setelah setiap langkah diambil. Misalkan di sini di program kami, alih-alih mengatakan "salah," akan ada pohon program yang kompleks, grafik aliran kontrol.



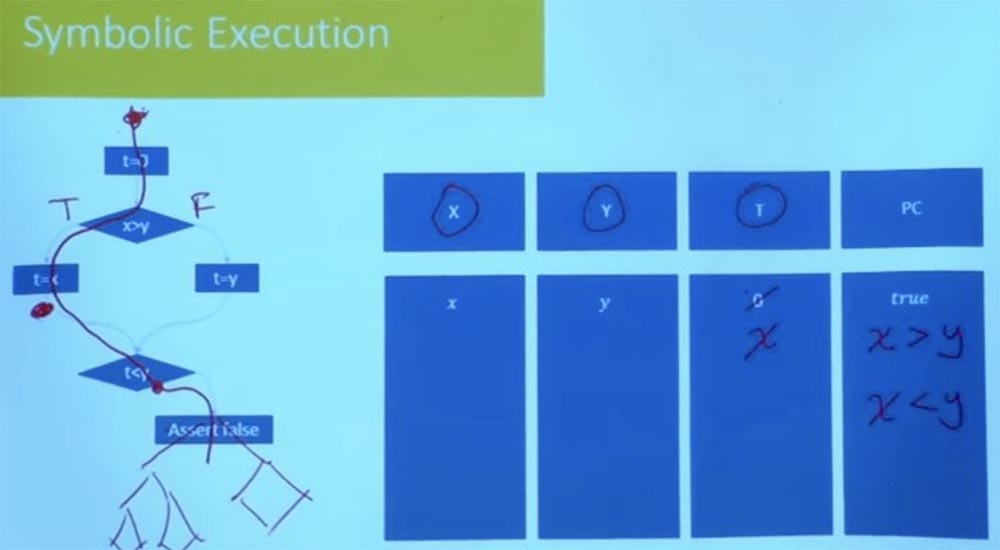
Anda tidak perlu menunggu sampai mencapai akhir untuk memverifikasi bahwa jalur ini layak. Pada saat itu, ketika Anda mencapai kondisi t <y, Anda sudah tahu bahwa jalan ini tidak memuaskan, dan Anda tidak akan pernah pergi ke arah itu. Oleh karena itu, memotong cabang yang salah pada awal program mengurangi jumlah pekerjaan empiris. Eksplorasi jalan yang wajar mencegah kemungkinan kegagalan program di masa depan. Banyak alat praktis yang digunakan saat ini terutama dimulai dengan pengujian acak untuk mendapatkan set jalan awal, setelah itu mereka akan mulai menjelajahi jalan di lingkungan. Mereka memproses banyak opsi untuk kemungkinan eksekusi program untuk masing-masing cabang, bertanya-tanya apa yang terjadi pada jalur ini.

Ini sangat berguna jika kita memiliki serangkaian tes yang baik. Anda menjalankan tes dan menemukan bahwa bagian kode ini tidak dieksekusi. Oleh karena itu, Anda dapat mengambil jalur yang paling dekat dengan implementasi kode dan bertanya apakah jalur ini dapat diubah sehingga berjalan ke arah yang benar?



Tetapi pada saat Anda mencoba untuk membuat semua jalur pada saat yang sama, pembatasan mulai yang menjadi sulit. Oleh karena itu, apa yang dapat Anda lakukan adalah melakukan satu fungsi pada satu waktu, sementara Anda dapat mempelajari semua jalur dalam suatu fungsi bersama. Jika Anda mencoba membuat balok besar, maka secara umum Anda dapat menjelajahi semua cara yang mungkin.

Yang paling penting adalah bahwa untuk setiap cabang Anda memeriksa batasan Anda dan menentukan apakah cabang ini benar-benar berjalan dua arah. Jika dia tidak bisa mengikuti kedua jalan, Anda menghemat waktu dan usaha dengan tidak mengikuti ke arah mana dia tidak bisa pergi. Selain itu, saya tidak ingat strategi khusus yang mereka gunakan untuk menemukan cara yang lebih mungkin menghasilkan hasil yang sangat baik. Tetapi memotong cabang yang salah pada tahap awal sangat penting.

Sampai sekarang, kita telah berbicara terutama tentang "kode mainan", tentang variabel integer, tentang cabang, tentang hal-hal yang sangat sederhana. Tetapi apa yang terjadi ketika Anda memiliki program yang lebih kompleks? Secara khusus, apa yang terjadi ketika Anda memiliki program yang mencakup banyak?



Secara historis, tumpukan pinggul telah menjadi kutukan dari semua analisis perangkat lunak karena hal-hal yang bersih dan elegan dari waktu Fortran meledak sepenuhnya ketika Anda mencoba menjalankannya menggunakan program C di mana Anda mengalokasikan memori kiri dan kanan. Di sana Anda memiliki overlay dan semua kekacauan yang terkait dengan program dengan memori yang dialokasikan dan dengan pointer aritmatika. Ini adalah salah satu bidang di mana eksekusi simbolis memiliki kemampuan luar biasa untuk beralasan tentang program.

Jadi bagaimana kita melakukan ini? Mari kita lupakan ranting-ranting dan kontrol aliran sejenak. Kami punya program sederhana di sini. Ini mengalokasikan sebagian memori, membatalkannya, dan mendapat pointer baru y dari pointer x. Kemudian dia menulis sesuatu ke y dan memeriksa apakah nilai yang disimpan dalam pointer y sama dengan nilai yang disimpan dalam pointer x?

Berdasarkan pengetahuan dasar tentang C, Anda dapat melihat bahwa pemeriksaan ini tidak dilakukan karena x diatur ulang dan y = 25, sehingga x menunjukkan lokasi yang berbeda. Sejauh ini, semuanya baik-baik saja dengan kami.
Cara kami memodelkan heap, dan cara heap dimodelkan pada kebanyakan sistem, menggunakan representasi heap di C, di mana itu hanyalah basis alamat raksasa, array raksasa di mana Anda dapat menempatkan data Anda.
Ini berarti bahwa kami dapat mewakili program kami sebagai dataset global yang sangat besar, yang akan disebut MEM. Ini adalah array yang pada dasarnya akan memetakan alamat ke nilai. Alamat hanya memiliki nilai 64-bit. Dan apa yang akan terjadi setelah Anda membaca sesuatu dari alamat ini? Itu tergantung pada bagaimana Anda memodelkan memori.

Jika Anda memodelkannya pada level byte, Anda mendapatkan byte. Jika Anda memodelkannya di level kata, Anda mendapatkan kata. Tergantung pada jenis kesalahan yang Anda minati, dan tergantung pada apakah Anda khawatir tentang alokasi memori atau tidak, Anda akan memodelkannya sedikit berbeda, tetapi biasanya memori hanyalah sebuah array dari alamat ke nilai.



Jadi alamatnya hanya bilangan bulat. Di satu sisi, tidak masalah apa yang C pikirkan tentang alamat, itu hanya bilangan bulat 64-bit atau 32-bit, tergantung pada mesin Anda. Ini hanyalah nilai yang diindeks dalam memori ini. Dan apa yang dapat Anda masukkan ke dalam memori, Anda dapat membaca dari memori itu.

Oleh karena itu, hal-hal seperti pointer aritmatika menjadi aritmatika integer. Dalam prakteknya, ada beberapa kesulitan, karena di C, pointer aritmatika tahu tentang tipe pointer, dan mereka akan meningkat secara proporsional dengan ukuran. Jadi, sebagai hasilnya, kami mendapatkan baris berikut:

y = x + 10;  sizeof (int)



Tetapi yang terpenting adalah apa yang terjadi ketika Anda menulis dan membaca dari ingatan. Berdasarkan pada penunjuk bahwa 25 harus ditulis dalam y, saya mengambil array memori dan mengindeksnya dengan y. Dan saya menulis 25 ke lokasi memori ini.

Kemudian saya beralih ke pernyataan MEM [y] = MEM [x], membaca nilai dari lokasi y dalam memori, membaca nilai dari lokasi x dalam memori, dan membandingkannya satu sama lain. Jadi saya periksa apakah cocok atau tidak.

Ini adalah asumsi yang sangat sederhana, memungkinkan Anda untuk beralih dari program yang menggunakan heap ke program yang menggunakan array global raksasa yang mewakili memori. Ini berarti bahwa sekarang, ketika berbicara tentang program yang mengelola heap, Anda benar-benar tidak perlu berbicara tentang program yang mengelola heap. Anda akan berhasil berbicara tentang array, dan bukan tentang tumpukan.

Ini pertanyaan sederhana lainnya. Bagaimana dengan fungsi malloc? Anda bisa mengambil dan menggunakan implementasi malloc di C, melacak semua halaman yang disorot, melacak semua yang telah dibebaskan, hanya memiliki daftar gratis, dan itu sudah cukup. Ternyata untuk banyak tujuan dan untuk banyak jenis kesalahan Anda tidak perlu malloc menjadi kompleks.

Bahkan, Anda dapat beralih dari malloc, yang terlihat seperti ini: x = malloc (sizeof (int) * 100), ke malloc semacam ini:

POS = 1
Int malloc (int n) {
rv = POS
POS + = n;
}

Yang hanya mengatakan: "Saya akan menyimpan konter untuk ruang kosong berikutnya dalam memori, dan setiap kali seseorang meminta alamat, saya memberinya lokasi ini dan meningkatkan posisi ini, dan kemudian mengembalikan rv." Dalam hal ini, apa yang malloc dalam pengertian tradisional benar-benar diabaikan.



Dalam hal ini, tidak ada memori yang membebaskan. Fungsi hanya terus bergerak lebih jauh dan lebih jauh dari memori, dan lebih jauh, dan lebih jauh, dan ini adalah di mana ia berakhir tanpa rilis apa pun. Dia juga tidak terlalu peduli bahwa ada area memori di mana itu tidak layak ditulis, karena ada alamat khusus yang sangat penting untuk sistem operasi.

Itu tidak memodelkan apa pun yang membuat penulisan fungsi malloc menjadi rumit, tetapi hanya pada tingkat abstraksi tertentu, ketika Anda mencoba untuk berbicara tentang beberapa jenis kode kompleks yang melakukan manipulasi pointer.

Pada saat yang sama, Anda tidak peduli tentang mengosongkan memori, tetapi Anda khawatir tentang apakah program akan, misalnya, menulis di luar buffer, dalam hal ini fungsi malloc ini bisa sangat baik.



Dan ini sebenarnya terjadi sangat, sangat sering ketika Anda melakukan eksekusi simbolik kode nyata. Langkah yang sangat penting adalah memodelkan fungsi perpustakaan Anda. Cara Anda memodelkan fungsi perpustakaan akan memiliki dampak besar, di satu sisi, pada kinerja dan skalabilitas analisis, tetapi di sisi lain, itu juga akan mempengaruhi akurasi.

Jadi jika Anda memiliki malloc model "mainan", seperti ini, itu akan bertindak sangat cepat, tetapi pada saat yang sama akan ada jenis kesalahan tertentu yang tidak dapat Anda perhatikan. Jadi, misalnya, dalam model ini saya sepenuhnya mengabaikan distribusi, jadi saya mungkin mendapatkan kesalahan jika seseorang mendapatkan akses ke ruang yang tidak terisi. Karena itu, dalam kehidupan nyata, saya tidak akan pernah menggunakan model malloc Mickey Mouse ini.

Jadi selalu ada keseimbangan antara akurasi analisis dan efisiensi. Dan semakin kompleks model fungsi standar, seperti yang didapatkan malloc, semakin kecil skalanya analisisnya. Tetapi untuk beberapa kelas kesalahan Anda perlu model-model sederhana ini. Oleh karena itu, berbagai perpustakaan di C sangat penting, yang diperlukan untuk memahami apa yang sebenarnya dilakukan oleh program semacam itu.

Oleh karena itu, kami mengurangi masalah penalaran tentang tumpukan dengan alasan tentang program dengan array, tetapi saya tidak benar-benar memberitahu Anda bagaimana berbicara tentang program dengan array. Ternyata sebagian besar SMT solver mendukung teori array.



Idenya adalah bahwa jika a adalah array, maka ada beberapa notasi yang memungkinkan Anda untuk mengambil array ini dan membuat array baru, di mana lokasi saya diperbarui ke nilai e. Apakah itu jelas?

Oleh karena itu, jika saya memiliki array a, dan saya melakukan operasi pembaruan ini, dan kemudian mencoba membaca nilai k, maka ini berarti bahwa nilai k akan sama dengan nilai k dalam array a, jika k berbeda dari i, dan itu akan sama dengan e, jika k sama dengan i.

Memperbarui array berarti Anda harus mengambil array lama dan memperbaruinya dengan array baru. Nah, jika Anda memiliki rumus yang mencakup teori array, itu sebabnya saya mulai dengan array nol, yang di mana-mana diwakili hanya oleh nol.



Kemudian saya menulis 5 ke lokasi i dan 7 ke lokasi j, setelah itu saya membaca dari k dan memeriksa apakah 5 atau tidak. Kemudian dapat diperluas menggunakan definisi untuk sesuatu yang mengatakan, misalnya: "jika k adalah i dan k adalah y, sedangkan k berbeda dari j, maka ya, itu akan menjadi 5, jika tidak maka tidak akan menjadi 5 ".

Dan dalam praktiknya, pemecah SMT tidak hanya memperluas ini ke banyak rumus Boolean, mereka menggunakan strategi bolak-balik antara pemecah SAT dan mesin, yang mampu berbicara tentang teori array untuk melakukan pekerjaan ini.

Yang penting adalah bahwa dengan mengandalkan teori array ini, menggunakan strategi yang sama yang kami terapkan untuk menghasilkan rumus untuk bilangan bulat, Anda sebenarnya dapat menghasilkan rumus yang mencakup logika array, pembaruan array, sumbu array, iterasi array. Dan selama Anda memperbaiki jalur Anda, rumus ini sangat mudah untuk dihasilkan.
Jika Anda tidak memperbaiki jalur Anda, tetapi ingin membuat formula yang sesuai dengan bagian dari program di sepanjang semua jalur, maka ini juga relatif mudah. Satu-satunya hal yang harus Anda hadapi adalah jenis loop khusus.

Kamus dan peta juga sangat mudah dimodelkan menggunakan fungsi yang tidak ditentukan. Sebenarnya, teori array itu sendiri hanyalah kasus khusus dari fungsi yang tidak terbatas. Dengan bantuan fungsi seperti itu, hal-hal yang lebih rumit dapat dilakukan. Dalam pemecah SMT modern, ada dukungan bawaan untuk alasan tentang set dan set operasi, yang bisa sangat berguna jika Anda berbicara tentang sebuah program yang mencakup set perhitungan.

Saat merancang salah satu alat ini, fase pemodelan sangat penting. Dan intinya bukan hanya bagaimana Anda memodelkan fungsi program yang kompleks ke teori Anda, misalnya, hal-hal seperti mengurangi tumpukan ke array. Intinya adalah teori dan pemecah mana yang Anda gunakan. Ada sejumlah besar teori dan pemecah masalah dengan hubungan yang berbeda, untuk itu perlu untuk memilih kompromi yang masuk akal antara efisiensi dan biaya.



Sebagian besar alat praktis mematuhi teori vektor bit dan, jika perlu, dapat menggunakan teori array untuk memodelkan tumpukan. Secara umum, alat praktis mencoba menghindari teori yang lebih kompleks, seperti teori himpunan. Ini karena mereka biasanya kurang terukur dalam beberapa kasus, jika Anda tidak berurusan dengan program yang benar-benar membutuhkan alat semacam ini untuk bekerja.

Audiens: selain studi tentang kinerja simbolik, apa yang menjadi fokus pengembang?

: — , . , , , , . , .

, , . , , , , , , , .

, — , , . , , — , JavaScript Python, . , .



, Python. , , : «, , , ». .

, , , , , .
, , , - , , .

, , , . , , Microsoft Word, , , .

, , , , .

, . , , - , - . , , . , .


Versi lengkap dari kursus ini tersedia di sini .

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps hingga Desember secara gratis ketika membayar untuk jangka waktu enam bulan, Anda dapat memesan di sini .

Dell R730xd 2 ? 2 Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 $249 ! . c Dell R730xd 5-2650 v4 9000 ?