Kursus MIT "Keamanan Sistem Komputer". Kuliah 10: Eksekusi Simbolik, Bagian 2

Institut Teknologi Massachusetts. Kursus Kuliah # 6.858. "Keamanan sistem komputer." Nikolai Zeldovich, James Mickens. Tahun 2014

Keamanan Sistem Komputer adalah kursus tentang pengembangan dan implementasi sistem komputer yang aman. Ceramah mencakup model ancaman, serangan yang membahayakan keamanan, dan teknik keamanan berdasarkan pada karya ilmiah baru-baru ini. Topik meliputi keamanan sistem operasi (OS), fitur, manajemen aliran informasi, keamanan bahasa, protokol jaringan, keamanan perangkat keras, dan keamanan aplikasi web.

Kuliah 1: “Pendahuluan: model ancaman” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 2: "Kontrol serangan hacker" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 3: “Buffer Overflows: Exploits and Protection” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 4: “Pemisahan Hak Istimewa” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 5: "Dari mana sistem keamanan berasal?" Bagian 1 / Bagian 2
Kuliah 6: “Peluang” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 7: “Kotak Pasir Klien Asli” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 8: “Model Keamanan Jaringan” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 9: "Keamanan Aplikasi Web" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 10: “Eksekusi simbolik” Bagian 1 / Bagian 2 / Bagian 3

Hadirin: Tampaknya Anda belum membicarakan tentang cara bit digunakan untuk menyimpan integer int.

Profesor: Ini pertanyaan yang sangat bagus. Dan itu benar-benar berkaitan dengan bagaimana Anda mendefinisikan keterbatasan Anda, bukan? Oleh karena itu, jika Anda melihat contoh sederhana kami dari awal, Anda akan melihat bahwa kami mengasumsikan kehadiran bilangan bulat yang kami pelajari di sekolah dasar. Pada saat yang sama, kami sepenuhnya memutuskan untuk mengabaikan kesalahan overflow. Jika Anda peduli tentang kesalahan overflow, dan penting bagi Anda bahwa tidak ada kesalahan seperti itu, maka menggunakan angka integer matematis tidak akan membantu untuk memperbaiki masalah.



Yang Anda butuhkan adalah menyajikan jumlah ini bukan sebagai bilangan bulat, tetapi sebagai vektor bit. Ketika Anda mewakili mereka sebagai vektor bit, Anda harus menggunakan pandangan yang lebih luas. Di sini kita kembali ke pemecah SMT. Aspek teori modular adalah bahwa pemecah itu sendiri dapat diperluas menggunakan teori yang berbeda.

Teori yang paling populer adalah teori vektor bit panjang tetap. Ini berarti bahwa jika Anda menginterpretasikan rumus Anda dalam teori vektor bit panjang tetap, Anda harus terlebih dahulu menetapkan panjang vektor bit. Artinya, Anda harus secara eksplisit menunjukkan bahwa ini akan digunakan untuk vektor bit yang panjangnya 32 bit, atau 8 bit, atau 64 bit.



Ada teori lain yang disebut teori array TOA. Dan kita akan berbicara sedikit tentangnya. Berbeda dengan teori bit vektor, yang dirancang untuk hal-hal dengan panjang tetap, teori array dimaksudkan untuk koleksi yang ukurannya tidak diketahui apriori.

Sekarang, dalam praktiknya, tidak ada yang menggunakan teori array, misalnya, untuk memodelkan bilangan bulat, karena terlalu mahal. Membicarakan masalah jauh lebih mahal ketika Anda tidak tahu batasannya. Oleh karena itu, sebagai suatu peraturan, orang menggunakan teori panjang vektor bit yang tetap dalam diskusi bilangan bulat atau bahkan simbol.

Teori lain yang sangat luas adalah teori aritmatika integer nyata, dan khususnya aritmatika integer linier.



Orang-orang sangat menyukai teori ini karena memberikan argumentasi yang efektif, tetapi tidak terlalu baik ketika Anda berbicara tentang program, karena di sini Anda benar-benar peduli dengan masalah meluap. Namun teori ini banyak digunakan untuk banyak hal.

Teori lain yang sering digunakan adalah teori fungsi yang tidak diinterpretasikan. Apa arti teori ini?



Itu artinya Anda memiliki formula tertentu. Dalam rumus ini, Anda tahu bahwa Anda memanggil suatu fungsi, tetapi Anda tidak tahu apa-apa tentang fungsi ini kecuali kenyataan bahwa jika Anda memasukkan beberapa input ke dalamnya, Anda akan mendapatkan output yang sama.

Ternyata ini sangat berguna ketika beralasan tentang hal-hal seperti menggunakan kode titik mengambang, pemodelan, sinus, cosinus, akar kuadrat. Diskusi terperinci tentang hal-hal seperti itu bisa sangat memakan waktu dan mahal. Tetapi menggunakan teori ini memungkinkan Anda untuk mengatakan: "Dengar, aku tidak terlalu peduli apa fungsi sinus. Saya tidak peduli apa tepatnya yang akan dia berikan. Saya hanya perlu tahu bahwa jika saya memanggil fungsi sinus di berbagai tempat program dengan input spesifik, saya akan mendapatkan data dari jenis yang sama di output. Ini cukup bagi saya untuk beralasan tentang program saya. ”

Dan oleh karena itu, operasi yang paling umum dalam analisis sistem nyata adalah vektor bit yang bekerja dengan integer, log, dan pointer. Bahkan, pointer sering diwakili oleh integer, karena kadang-kadang Anda tidak menetapkan bit vektor pada pointer. Tetapi kadang-kadang Anda harus melakukan ini, dan kemudian Anda tidak bisa lagi menggunakan bilangan bulat.

Jadi, kami memeriksa apa yang dapat dilakukan oleh pemecah SMT untuk Anda. Bagaimana cara kerjanya? Apa yang ada di dalam diri mereka yang membuat mereka bekerja?

Faktanya, pemecah SMT mengandalkan kemampuan kami untuk memecahkan masalah kelayakan rumus SAT Boolean, pada kemampuan untuk mempertimbangkan masalah yang terkait hanya dengan kendala Boolean murni dan variabel Boolean, dan beri tahu kami apakah Anda akan memastikan bahwa program memberikan nilai yang ditetapkan ke variabel Boolean ini atau tidak. .

Ini adalah sesuatu yang selama bertahun-tahun mengajar siswa senior, mengatakan bahwa ini sebenarnya adalah tugas NP-lengkap, dan dalam kasus di mana sesuatu turun ke SAT, Anda tidak boleh melakukan ini. Tetapi ternyata kami memiliki pemecah SAT yang sangat baik.

Jadi, saya akan memberi tahu Anda ide dasar tentang cara kerja pemecah SAT. Itu terletak pada kenyataan bahwa Anda mengambil semua batasan Anda pada variabel Boolean dan memasukkannya ke dalam basis data. Anda mungkin tidak dapat melihat huruf-huruf kecil di layar dengan jelas, tetapi hanya itu yang bisa saya lakukan.



Saya akan berkomentar dan membicarakannya selama aksi, dan kemudian saya akan mempublikasikan slide sehingga Anda dapat melihat apa yang tertulis di sana.

Jadi, di sini dalam tugas SAT kita memiliki semua variabel ini mewakili Boolean tidak diketahui, kan? Kami ingin tahu apakah X mungkin benar pada saat yang sama (X = BENAR), dan Y menjadi benar, dan Z menjadi benar. Ini adalah tidak diketahui kita. Selain itu, semua batasan dalam bentuk konjungtif normal. Ini berarti bahwa semua batasan kami adalah dalam bentuk X1 = true, atau X2 = true, atau X3 = true.



Dalam formulir ini, kami memiliki semua keterbatasan kami, yang mengatakan bahwa X1 benar, atau X2 salah, atau X3 salah. Anda mungkin ingat dari matematika diskrit bahwa rumus Boolean dapat direpresentasikan dalam bentuk ikat normal. Ini berarti bahwa setiap representasi yang Anda gunakan untuk mewakili formula Boolean, Anda dapat dengan mudah mengonversi ke format ini.

Jadi, kami memiliki database dengan banyak batasan dari formulir ini. Pemecah SAT akan memilih salah satu dari variabel-variabel ini secara acak, misalkan X1. Dan dia akan berkata: "mengapa tidak mengatur X1 menjadi kenyataan? Saya tidak tahu apa-apa tentang pembatasan ini, jadi saya bisa berasumsi bahwa ini memang benar. " Dan kemudian terjadi bahwa Anda akan memiliki batasan yang, misalnya, menyatakan bahwa X1 salah atau X7 benar.

Jadi, jika Anda tahu bahwa X1 benar dan Anda tahu bahwa X1 salah atau X7 benar, apa yang Anda ketahui tentang X7?

Hadirin: itu pasti benar!

Profesor: ya, itu pasti benar. Karena kalau tidak maka batasan ini tidak akan dipenuhi. Jadi, sekarang Anda telah mendistribusikan nilai ini dari X1 ke X7. Misalkan Anda sekarang memilih variabel acak lain, seperti X5.



Sekarang anggaplah Anda memiliki batasan yang mengatakan: X7 salah, atau X6 benar, atau X5 salah. Jadi, saya punya X5 = benar dan X7 = benar. Ini berarti bahwa X6 sekarang juga harus benar. Karena kalau tidak maka pembatasan ini akan dilanggar. Jadi, sistem menyimpulkan bahwa X6 harus benar, dan melanjutkan proses, melakukan pemeriksaan yang tersedia dan melihat semua penawaran yang tersedia. Sistem memeriksa apakah ada hal-hal lain yang tersirat oleh cek yang dimilikinya. Dan dia mengikuti makna ini sampai satu dari dua hal terjadi.

Yang pertama adalah Anda terus mengikuti konsekuensi dan mencoba hal-hal acak, dan akhirnya Anda menetapkan nilai untuk setiap variabel tanpa pernah menemui kontradiksi. Jadi Anda melakukan segalanya dengan benar.

Yang kedua - Anda dihadapkan dengan kontradiksi, dan kemudian Anda kembali ke kondisi yang membuat X4 benar, tidak termasuk kondisi yang membuat X4 salah. Tetapi ada satu aturan aljabar Boolean yang harus diketahui semua orang: variabel tidak bisa benar dan salah pada saat yang sama.



Dan dikatakan bahwa Anda dihadapkan dengan kontradiksi, Anda jelas melakukan sesuatu yang salah dalam salah satu tugas acak yang Anda coba selesaikan ini.

Mari kita menganalisis kontradiksi ini dan melihat tugas apa yang menyebabkan kontradiksi ini. Berdasarkan penugasan yang menyebabkan kontradiksi ini, mari kita membuat klausul konflik baru yang merangkum kontradiksi ini.

Apa yang terjadi bahwa X1 salah, dan X5 salah, dan X9 juga salah? Pada dasarnya, ini didasarkan pada apa yang saya pelajari dari tugas acak ini, di mana saya menemukan bahwa salah satu dari hal-hal ini harus benar, bahwa tidak mungkin X1 benar dan X5 benar, dan X9 adalah salah, ini tidak mungkin.

Saya tahu ini tidak dapat terjadi, karena ketika saya mencoba melakukannya, semuanya “meledak”, saya mengakhiri program dengan kontradiksi.

Jadi, pemecah SAT mencoba menyelesaikan tugas acak, memeriksa bagaimana hasilnya. Ketika dia menghadapi kontradiksi, dia menganalisis serangkaian konsekuensi yang mengarah pada kontradiksi ini, dan akhirnya membentuk batasan baru, yang memastikan bahwa pemecah tidak pernah lagi menghadapi kontradiksi khusus ini, masalah khusus ini.
Dengan demikian, kita dapat membayangkan pemecah SAT sebagai "kotak hitam" yang memberikan batasan Boolean dan dapat mengetahui apakah itu memuaskan atau tidak. Solver SMT dibangun di atas solver SAT terbaik. Mereka dapat menggunakan kekuatan pemecah SAT untuk menyelesaikan masalah NP-lengkap dengan alasan berorientasi subjek tentang teori yang didukung.

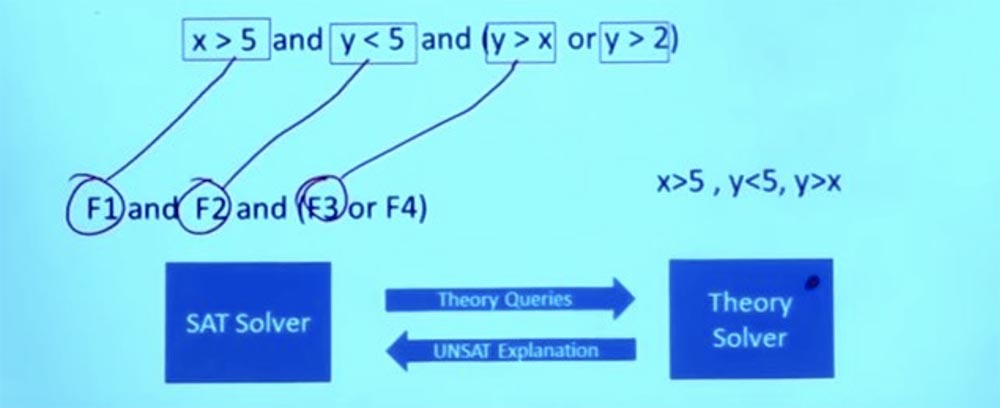
Untuk mendapatkan ide tentang bagaimana ini bekerja, anggaplah Anda memiliki formula seperti itu.



Apakah bisa dilakukan? Bisakah kita menemukan tes yang memuaskan untuknya? Pemecah SMT dapat memisahkan bagian dari rumus ini, yang memerlukan penalaran dalam teori bilangan bulat. Kami menggunakan struktur Boolean untuk memisahkan formula. Jadi kami memiliki rumus F1, F2, F3 dan F4.



Sekarang ini adalah tugas Boolean yang murni logis - dapatkah saya menemukan tugas yang memuaskan untuk ini? Pemecah SAT dapat mengatakan: "Ya, saya dapat menemukan sesuatu yang memuaskan tugas ini dengan melakukan F1 = benar, F2 = benar dan F3 = benar." Ini memenuhi spesifikasi formula Boolean.

\

Jadi, sekarang kita memiliki pertanyaan yang dapat kita tanyakan kepada pemecah untuk area tertentu, dalam hal ini hanya pemecah aritmatika linier. Jadi kita bisa pergi ke pemecah teori Theory dan mengatakan: "Pemecah SAT mengklaim bahwa ini adalah tugas yang masuk akal, dan bahwa jika saya dapat membuat tugas ini berhasil, maka rumus saya akan terpenuhi."

Saya dapat mengatakan bahwa F1 adalah X> 5, F2 adalah Y <5, dan F3 adalah Y> X. Jadi saya dapat bertanya kepada pemecah SAT apakah mungkin untuk mendapatkan X dan Y sehingga X adalah> 5, Y adalah < 5, dan dalam hal ini Y akan menjadi> X? Sekarang ini adalah pertanyaan aritmatika linier murni, tidak ada logika Boolean.

Dan apa jawaban untuk pertanyaan ini? Tidak. Tidak mungkin untuk memenuhi kondisi ini pada saat yang bersamaan.
Jadi, ada metode tradisional untuk memecahkan masalah linier. Anda dapat menggunakan metode simpleks, misalnya, untuk menyelesaikan sistem ketidaksetaraan linear. Ada banyak metode yang dapat digunakan untuk menyelesaikan sistem ketidaksetaraan linear.



Jadi, pemecah SAT mengirim pertanyaan teoretis ke pemecah Teori. Intinya adalah bahwa pemecah teori tahu semua tentang masalah ini dan dapat memberikan jawaban yang akurat untuk pertanyaan apakah kondisi ini akan berhasil.

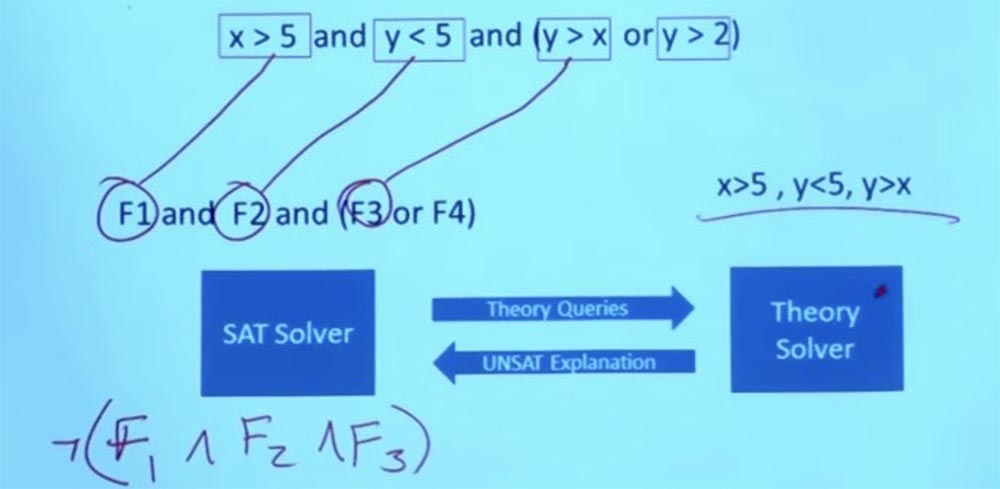
Dalam kasus ini, pemecah teori memproses permintaan, menemukan bahwa penetapan kondisi ini tidak dapat berfungsi, kembali ke pemecah SAT dan berkata: "hal-hal yang Anda lakukan tidak akan berhasil"!

Tetapi dia tidak hanya mengatakan ya atau tidak, tetapi menjelaskan mengapa sesuatu tidak akan berhasil. Dari kenyataan bahwa rumus-rumus ini tidak berfungsi, pemecah Teori menyimpulkan bahwa F1 dan F2 dan F3 tidak dapat ada secara bersamaan, dan memberi tahu pemecah SAT bahwa ketiga rumus ini saling eksklusif.

Jadi sekarang kita memiliki beberapa informasi yang saya dapat kembali ke pemecah SAT dan bertanya kepadanya: "Hei, Anda bisa memberi saya solusi yang memuaskan tidak hanya kendala yang kami miliki di awal, tetapi juga kendala baru yang ditemukan oleh Teori pemecah "?

Apakah ada tujuan lain yang sekarang memenuhi kedua keterbatasan ini?



Jadi, kita membuang batasan awal X> 5, Y <5, Y> X, ini tidak mengganggu kita lagi.



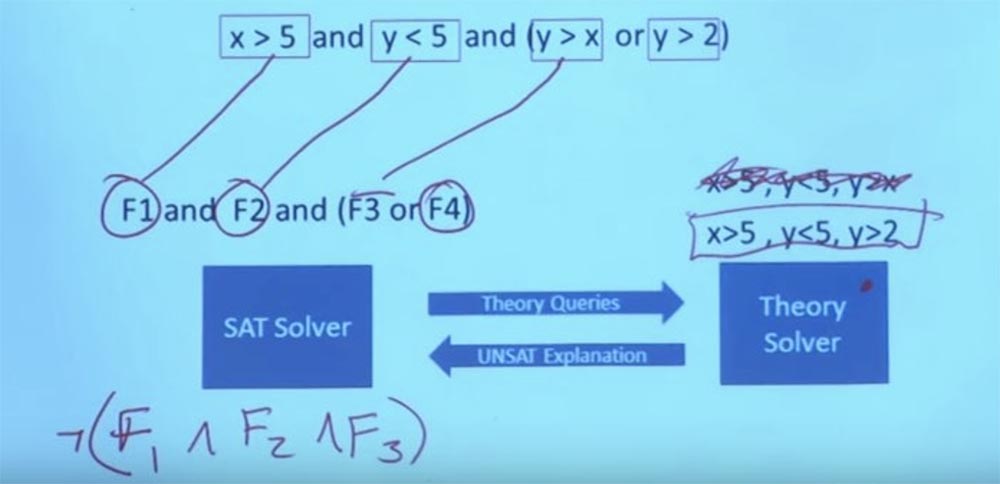
Kami memiliki batasan baru yang dapat kami atur ke pemecah Teori kami - X> 5, Y <5, Y> 2. Kita dapat membuat Y sama dengan 3, dan X sama dengan 6, dan kemudian itu akan bekerja. Sekarang Anda memiliki tugas yang memenuhi formula dalam teori dan memenuhi struktur Boolean dari tujuan ini. Dan dengan itu, sistem dapat kembali dan berkata: "Ya, ini adalah tugas yang memenuhi semua keterbatasan Anda." Ini adalah interaksi antara pemecah Teori dan pemecah SAT. Pada kenyataannya, ini berarti dapat berbicara tentang formula Boolean yang sangat, sangat besar dan sangat kompleks. Inilah yang memungkinkan eksekusi simbolis.

Sekarang kita akan mempertimbangkan pertanyaan berikutnya - bagaimana transisi dari program ke pembatasan yang dapat kami berikan untuk pemecah SMT dilakukan.

Hadirin: Apakah membangun NP SM solver selesai atau tidak?

Profesor: Pemecah SMT pada dasarnya adalah masalah NP-kanonik lengkap. Tetapi kebanyakan pemecah masalah hari ini termasuk dukungan untuk teori-teori tertentu yang benar-benar tidak dapat dipecahkan.

Pemirsa: bagaimana Anda mendekati masalah ini di sistem Anda?

Profesor: baik, pada akhirnya, Anda akan mendapatkan batasan yang dibuat dari program ini. Anda akan memberikannya ke pemecah SMT. Dan fakta bahwa ini adalah tugas-tugas NP-lengkap atau fakta bahwa mereka tidak memuaskan berarti bahwa jika Anda beruntung Anda akan menerima jawaban dalam hitungan detik. Tetapi jika Anda tidak beruntung, maka mungkin butuh waktu lebih lama daripada penciptaan alam semesta.



Audiens: apakah itu terjadi bahwa tugas-tugas sistem linear tidak lulus SAT?

Profesor: ya, itu benar-benar terjadi. Namun, alat-alat teknik yang ada membuatnya kurang umum. Kami tidak memecahkan masalah acak SAT, kami tidak memecahkan masalah vektor bit sepenuhnya acak.

Kami memecahkan masalah yang memiliki struktur tertentu sehingga seseorang dapat melihatnya dan memiliki keyakinan bahwa itu akan berhasil. Kami mencoba membuat beberapa argumen di kepalanya untuk memahami mengapa ini berhasil. Dan pemecah SAT menggunakan struktur ini. Masalah Anda mungkin memiliki sejuta variabel Boolean, tetapi dalam kenyataannya sebagian besar variabel ini sangat bergantung pada nilai masing-masing. Dengan demikian, jumlah derajat kebebasan dalam masalah sebenarnya jauh lebih sedikit daripada yang disarankan jutaan variabel.

Hadirin: Anda mengatakan bahwa ini bukan pertanyaan ujian, tetapi kehidupan nyata. Setelah seseorang membangun sistem ini, itu harus bekerja dan masuk akal. Jadi ini mungkin tidak akan menjadi salah satu teori yang tidak perlu.

Profesor: itu dia. Karena itu, dalam praktiknya, saat Anda menggunakan alat ini, yang selalu Anda lakukan adalah mengatur batas waktu. Secara umum, semuanya terjadi karena eksponensial tidak berarti Anda tidak dapat melakukan ini. Eksponensialitas, yaitu, ketika satu fungsi dibatasi oleh fungsi lain, hanya berarti bahwa ada dinding bata di depannya yang dapat berfungsi, dan mereka akan bekerja dengan sangat cepat. Eksponensialitas bekerja di kedua arah.



Ketika Anda menjauh dari tembok ini, banyak hal tumbuh sangat cepat, tetapi ketika Anda mendekati masalah yang lebih kecil atau lebih sederhana, masalah ini juga berakselerasi dengan sangat, sangat cepat. Ini berarti bahwa banyak masalah berakhir dengan sangat cepat. Dan kemudian masalah timeout terjadi. Intinya adalah untuk merancang hal-hal sehingga di antara masalah yang cepat berakhir adalah mereka yang membawa manfaat praktis. Ini adalah masalah yang mengarahkan Anda ke kerentanan keamanan sistem Anda, kesalahan, ke jalur yang mungkin belum pernah Anda jelajahi sebelumnya, atau untuk masukan yang akan melanggar jalur Anda jika Anda tidak memeriksanya terlebih dahulu.

Jadi, kita tahu bagaimana beralih dari formula, dari serangkaian batasan ke jawaban yang mengatakan: "Ya, formula ini memiliki solusi, dan ini dia, ini solusi." Atau dia akan berkata: "formula ini tidak memuaskan, karena tidak ada input yang memuaskan tugas Anda." Jadi bagaimana kita mendapatkan formula dari program ini?

Saat Anda melakukan eksekusi simbolis, Anda pergi ke cabang dan tidak tahu ke mana arahnya. Ada dua opsi untuk apa yang harus dilakukan dalam kasus ini. — , , , .

, , . , SMT-. . , .

: « , , , , ».

, , . . , .

, . , , . , – , . ? , .



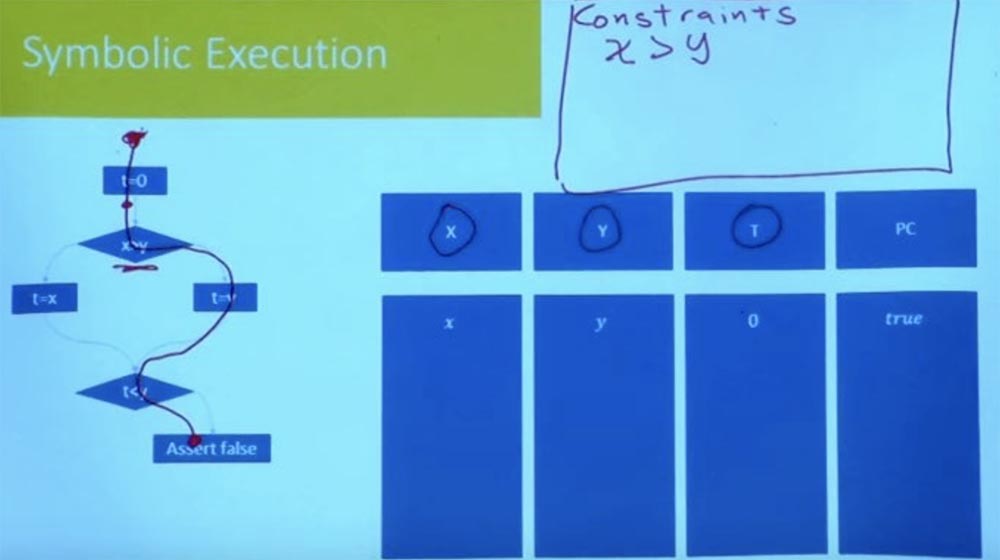
, , t=0 false.



, , ? : , , .

, , , , , , .

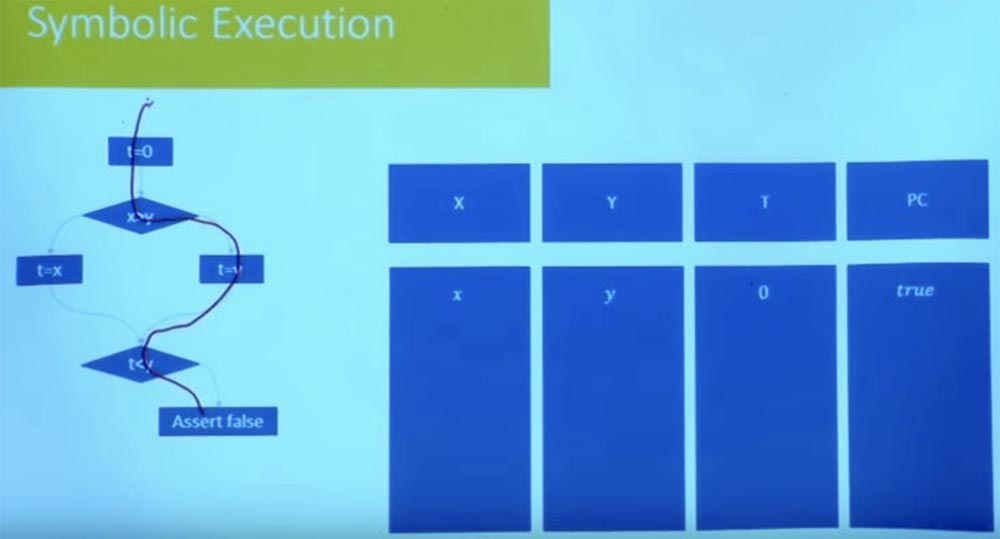
, , t = 0, x, y 0. , . , , X , Y.

, X > Y.



55:00

MIT « ». 10: « », 3


Versi lengkap dari kursus ini tersedia di sini .

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps hingga Desember secara gratis ketika membayar untuk jangka waktu enam bulan, Anda dapat memesan di sini .

Dell R730xd 2 kali lebih murah? Hanya kami yang memiliki 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV dari $ 249 di Belanda dan Amerika Serikat! Baca tentang Cara Membangun Infrastruktur Bldg. kelas menggunakan server Dell R730xd E5-2650 v4 seharga 9.000 euro untuk satu sen?