Game Theory: Pengambilan Keputusan dengan Contoh di Kotlin

Teori permainan adalah disiplin matematika yang mempertimbangkan pemodelan tindakan pemain yang memiliki tujuan, yaitu memilih strategi optimal untuk perilaku dalam suatu konflik. Mengenai Habré, topik ini sudah dibahas , tetapi hari ini kita akan membahas beberapa aspeknya secara lebih rinci dan mempertimbangkan contoh-contoh di Kotlin.

Jadi, strategi adalah seperangkat aturan yang menentukan pilihan tindakan untuk setiap langkah pribadi, tergantung pada situasinya. Strategi pemain yang optimal adalah strategi yang memastikan posisi terbaik dalam permainan yang diberikan, mis. keuntungan maksimum. Jika permainan diulang beberapa kali dan berisi, selain gerakan pribadi, acak, maka strategi optimal memberikan kemenangan rata-rata maksimum.

Tugas teori permainan adalah mengidentifikasi strategi optimal untuk pemain. Asumsi utama atas dasar strategi optimal ditemukan adalah bahwa lawan (atau lawan) tidak kurang cerdas dari pemain itu sendiri dan melakukan segalanya untuk mencapai tujuannya. Perhitungan lawan yang masuk akal hanyalah salah satu posisi potensial dalam konflik, tetapi dalam teori permainan, hal itulah yang diletakkan di dasar.

Ada permainan dengan sifat di mana hanya ada satu peserta yang memaksimalkan keuntungan mereka. Game dengan alam adalah model matematika di mana pilihan solusi tergantung pada realitas objektif. Misalnya, permintaan konsumen, keadaan alam, dll. "Alam" adalah konsep umum dari musuh yang tidak mengejar tujuannya sendiri. Dalam hal ini, beberapa kriteria digunakan untuk memilih strategi optimal.
Ada dua jenis tugas dalam game dengan alam:

1. tugas membuat keputusan dalam kondisi risiko ketika probabilitas yang diterima sifatnya masing-masing negara yang mungkin diketahui;
2. tugas pengambilan keputusan dalam kondisi ketidakpastian, ketika tidak mungkin untuk mendapatkan informasi tentang kemungkinan terjadinya keadaan alamiah.

Secara singkat tentang kriteria ini dijelaskan di sini .

Sekarang kita akan mempertimbangkan kriteria pengambilan keputusan dalam strategi murni, dan pada akhir artikel kita akan menyelesaikan permainan dalam strategi campuran dengan metode analitis.

Pernyataan masalah

Kami akan menganalisis semua kriteria pengambilan keputusan menggunakan contoh melalui. Tugasnya adalah ini: petani perlu menentukan dalam proporsi apa untuk menanam ladangnya dengan tiga tanaman, jika hasil panen ini, dan, oleh karena itu, keuntungannya, tergantung pada bagaimana musim panas akan: dingin dan hujan, normal, atau panas dan kering. Petani menghitung laba bersih dari 1 hektar dari berbagai tanaman tergantung pada cuaca. Permainan ditentukan oleh matriks berikut:



Selanjutnya kami akan menyajikan matriks ini dalam bentuk strategi:

$$

$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$$

Strategi optimal yang diinginkan dilambangkan dengan $$$u_ {opt}$ . Kami akan menyelesaikan permainan menggunakan kriteria Wald, optimisme, pesimisme, Savage, dan Hurwitz dalam kondisi ketidakpastian dan kriteria Bayes dan Laplace dalam kondisi risiko.

Seperti disebutkan di atas, contohnya ada di Kotlin. Saya perhatikan bahwa secara umum ada solusi seperti Gambit (ditulis dalam C), Axelrod dan PyNFG (ditulis dengan Python), tetapi kita akan mengendarai sepeda kita sendiri, berkumpul di lutut, hanya untuk menyodok sedikit gaya, modis dan bahasa pemrograman pemuda.

Untuk mengimplementasikan solusi permainan secara terprogram, kami akan memperkenalkan beberapa kelas. Pertama, kita membutuhkan kelas yang memungkinkan kita untuk mendeskripsikan baris atau kolom dari matriks game. Kelas ini sangat sederhana dan berisi daftar nilai yang mungkin (alternatif atau keadaan alami) dan nama yang sesuai. Bidang key akan digunakan untuk identifikasi, serta untuk perbandingan, dan perbandingan akan diperlukan dalam pelaksanaan dominasi.


Matriks permainan berisi informasi tentang alternatif dan keadaan alami. Selain itu, ia mengimplementasikan beberapa metode, misalnya, menemukan set dominan dan harga bersih game.


Kami menggambarkan antarmuka yang memenuhi kriteria

Pengambilan keputusan di bawah ketidakpastian

Membuat keputusan dalam menghadapi ketidakpastian menunjukkan bahwa pemain tidak ditentang oleh lawan yang masuk akal.

Kriteria Wald

Kriteria Wald memaksimalkan hasil yang paling buruk:

$$

$$u_ {opt} = max_ {i} min_ {j} [U]$$

Menggunakan kriteria mengasuransikan hasil terburuk, tetapi harga dari strategi seperti itu adalah hilangnya kesempatan untuk mendapatkan hasil terbaik.

Pertimbangkan sebuah contoh. Untuk strategi $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ temukan posisi terendah dan dapatkan tiga berikutnya $$$S = (0, 1, -1)$ . Maksimum untuk triple yang ditunjukkan adalah nilai 1, oleh karena itu, menurut kriteria Wald, strategi yang menang adalah strategi $$$U_ {2} = (2,3,1)$ sesuai dengan Budaya Tanam 2.

Implementasi perangkat lunak kriteria Wald sederhana:

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } } 

Demi kejelasan, untuk pertama kalinya saya akan menunjukkan bagaimana solusi akan terlihat seperti tes:


Mudah ditebak bahwa untuk kriteria lain, perbedaannya hanya ada pada penciptaan objek criteria .

Kriteria optimisme

Ketika menggunakan kriteria seorang optimis, pemain memilih solusi yang memberikan hasil terbaik, sementara optimis menganggap bahwa kondisi permainan akan paling menguntungkan baginya:

$$

$$u_ {opt} = max_ {i} max_ {j} [U]$$

Strategi optimis dapat mengakibatkan konsekuensi negatif ketika pasokan maksimum bertepatan dengan permintaan minimum - perusahaan dapat menerima kerugian ketika menghapus produk yang tidak terjual. Pada saat yang sama, strategi optimis memiliki arti tertentu, misalnya, Anda tidak perlu mengurus pelanggan yang tidak puas, karena setiap permintaan yang mungkin selalu dipenuhi, oleh karena itu tidak perlu mempertahankan lokasi pelanggan. Jika permintaan maksimum terwujud, maka strategi optimis memungkinkan Anda untuk mendapatkan utilitas maksimum sementara strategi lain akan menyebabkan hilangnya laba. Ini memberikan keunggulan kompetitif tertentu.

Pertimbangkan sebuah contoh. Untuk strategi $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ temukan, temukan maksimum dan dapatkan tiga berikutnya $$$S = (5, 3, 4)$ . Maksimum untuk triple yang ditunjukkan adalah nilai 5, oleh karena itu, menurut kriteria optimisme, strategi yang menang adalah strategi $$$U_ {1} = (0.2.5)$ sesuai dengan Budaya Tanam 1.

Penerapan kriteria optimisme hampir tidak berbeda dengan kriteria Wald

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } } 

Kriteria pesimisme

Kriteria ini dimaksudkan untuk memilih elemen terkecil dari matriks game dari elemen minimum yang mungkin:

$$

$$u_ {opt} = min_ {i} min_ {j} [U]$$

Kriteria pesimisme menunjukkan bahwa perkembangan acara tidak akan menguntungkan bagi pembuat keputusan. Ketika menggunakan kriteria ini, pembuat keputusan dipandu oleh kemungkinan hilangnya kendali atas situasi, oleh karena itu, ia mencoba untuk mengecualikan risiko potensial dengan memilih opsi dengan profitabilitas minimal.

Pertimbangkan sebuah contoh. Untuk strategi $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ temukan, temukan yang minimum dan dapatkan tiga berikutnya $$$S = (0, 1, -1)$ . Minimum untuk triple yang ditunjukkan adalah nilai -1, oleh karena itu, menurut kriteria pesimisme, strategi yang menang adalah strategi $$$U_ {3} = (4.3, -1)$ sesuai dengan Budaya Tanam 3.

Setelah mengetahui kriteria dan optimisme Wald, mudah untuk menebak bagaimana kelas kriteria pesimisme akan terlihat seperti:

 class PessimismCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val min = mins.minWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == min!!.second } .map { m -> m.first } } } 

Kriteria Savage

Kriteria Savage (kriteria pesimistis pesimis) melibatkan meminimalkan laba yang hilang terbesar, dengan kata lain, penyesalan terbesar atas laba yang hilang diminimalkan:

$$

$$u_ {opt} = min_ {i} max_ {j} [S] \\ s_ {i, j} = (maks \ begin {bmatrix} u_ {1, j} \\ u_ {2, j} \\. .. \\ u_ {n, j} \ end {bmatrix} - u_ {i, j})$$

Dalam hal ini, S adalah matriks penyesalan.

Solusi optimal menurut kriteria Savage harus memberikan penyesalan paling sedikit dari penyesalan yang ditemukan pada langkah sebelumnya. Solusi yang sesuai dengan utilitas yang ditemukan akan optimal.

Fitur dari solusi yang diperoleh termasuk tidak adanya kekecewaan terbesar yang dijamin dan penurunan dijamin dalam kemenangan maksimum yang mungkin dari pemain lain.

Pertimbangkan sebuah contoh. Untuk strategi $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ buat matriks penyesalan:



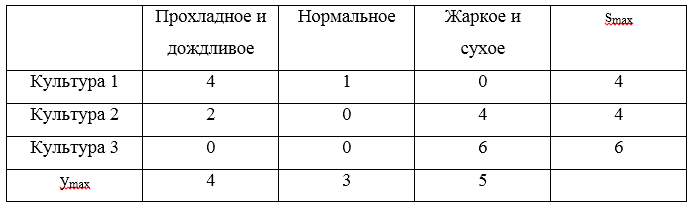
Tiga penyesalan maksimal $$$S = (4,4,6)$ . Nilai minimum risiko ini adalah nilai 4, yang sesuai dengan strategi $$$U_ {1}$ dan $$$U_ {2}$ .

Memprogram tes Savage sedikit lebih sulit:

 class SavageCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.risk(): List<Pair<GameVector, Double?>> { val maxStates = this.natureStates.map { n -> Pair(n, n.values.max()) } .map { n -> n.first.key to n.second }.toMap() var am: MutableList<Pair<GameVector, List<Double>>> = mutableListOf() for (a in this.alternatives) { var v: MutableList<Double> = mutableListOf() for (i in 0..a.values.lastIndex) { val mn = maxStates.get(i) v.add(mn!! - a.values[i]) } am.add(Pair(a, v.toList())) } return am.map { m -> Pair(m.first, m.second.max()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.risk() val minRisk = risk.minWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == minRisk!!.second } .map { m -> m.first } } } 

Kriteria Hurwitz

Kriteria Hurwitz adalah kompromi yang diatur antara pesimisme ekstrem dan optimisme total:

$$

$$u_ {opt} = maks (\ gamma × A (k) + A (0) × (1 - \ gamma))$$

A (0) adalah strategi pesimis ekstrem, A (k) adalah strategi optimis penuh, $$$\ gamma = 1$ - Nilai set koefisien berat: $$$0 \ leq \ gamma \ leq1$ ; $$$\ gamma = 0$ - pesimisme ekstrim, $$$\ gamma = 1$ - optimisme penuh.

Dengan sejumlah kecil strategi tersendiri, atur nilai koefisien bobot yang diinginkan $$$\ gamma$ , dan kemudian bulatkan hasilnya ke nilai terdekat yang mungkin, dengan mempertimbangkan diskritisasi yang dilakukan.

Pertimbangkan sebuah contoh. Untuk strategi $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ . Kami berasumsi bahwa koefisien optimisme $$$\ gamma = $ 0,$ . Sekarang buat tabel:



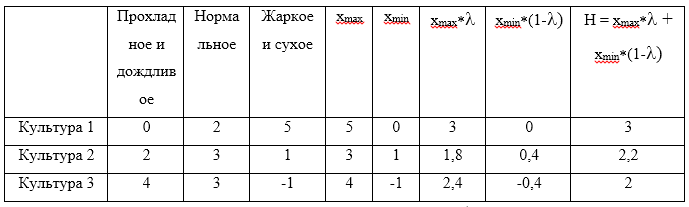
Nilai maksimum dari H yang dihitung akan menjadi nilai 3, yang sesuai dengan strategi $$$U_ {1}$ .

Penerapan kriteria Hurwitz sudah lebih banyak:

 class HurwitzCriteria(gameMatrix: GameMatrix, optimisticKoef: Double) : ICriteria { val gameMatrix: GameMatrix val optimisticKoef: Double init { this.gameMatrix = gameMatrix this.optimisticKoef = optimisticKoef } inner class HurwitzParam(xmax: Double, xmin: Double, optXmax: Double){ val xmax: Double val xmin: Double val optXmax: Double val value: Double init{ this.xmax = xmax this.xmin = xmin this.optXmax = optXmax value = xmax * optXmax + xmin * (1 - optXmax) } } fun GameMatrix.getHurwitzParams(): List<Pair<GameVector, HurwitzParam>> { return this.alternatives.map { a -> Pair(a, HurwitzParam(a.max()!!, a.min()!!, optimisticKoef)) } } override fun optimum(): List<GameVector> { val hpar = gameMatrix.getHurwitzParams() val maxHurw = hpar.maxWith(Comparator { o1, o2 -> o1.second.value.compareTo(o2.second.value) }) return hpar .filter { r -> r.second == maxHurw!!.second } .map { m -> m.first } } } 

Pengambilan keputusan berisiko

Metode pengambilan keputusan dapat mengandalkan kriteria untuk pengambilan keputusan dalam kondisi risiko, tunduk pada kondisi berikut:

• kurangnya informasi yang dapat dipercaya tentang kemungkinan konsekuensi;
• adanya distribusi probabilitas;
• pengetahuan tentang kemungkinan hasil atau konsekuensi untuk setiap keputusan.

Jika keputusan dibuat dalam kondisi risiko, maka biaya keputusan alternatif dijelaskan oleh distribusi probabilitas. Dalam hal ini, keputusan didasarkan pada penggunaan kriteria nilai yang diharapkan, yang menurutnya solusi alternatif dibandingkan dalam hal memaksimalkan keuntungan yang diharapkan atau meminimalkan biaya yang diharapkan.

Kriteria nilai yang diharapkan dapat dikurangi baik untuk memaksimalkan laba (rata-rata) yang diharapkan, atau untuk meminimalkan biaya yang diharapkan. Dalam hal ini, diasumsikan bahwa laba (biaya) yang terkait dengan setiap solusi alternatif adalah variabel acak.

Perumusan tugas-tugas tersebut biasanya sebagai berikut: seseorang memilih tindakan apa pun dalam situasi di mana peristiwa acak memengaruhi hasil tindakan. Tetapi pemain memiliki beberapa pengetahuan tentang probabilitas peristiwa ini dan dapat menghitung kombinasi dan urutan tindakannya yang paling menguntungkan.

Untuk terus memberikan contoh, kami melengkapi matriks game dengan probabilitas:



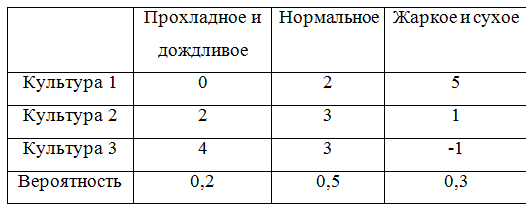
Untuk memperhitungkan probabilitas, kelas yang menggambarkan matriks game harus diulang sedikit. Ternyata, sebenarnya, tidak terlalu elegan, tapi oh well.

Kriteria bayes

Kriteria Bayes (kriteria harapan) digunakan dalam masalah pengambilan keputusan dalam kondisi risiko sebagai penilaian strategi $$$u_ {i}$ ekspektasi matematis dari variabel acak yang sesuai muncul. Menurut aturan ini, strategi pemain optimal $$$u_ {opt}$ ditemukan dari kondisi:

$$

$$u_ {opt} = max_ {1 \ leq i \ leq n} M (u_ {i}) \\ M (u_ {i}) = max_ {1 \ leq i \ leq n} \ sum_ {j = 1} ^ m u_ {i, j} \ cdot y_ {j} ^ 0$$

Dengan kata lain, indikator inefisiensi strategi $$$u_ {i}$ menurut Bayes kriteria mengenai risiko adalah nilai rata-rata (ekspektasi) dari risiko baris ke-i $$$U$ yang probabilitasnya bertepatan dengan probabilitas alam. Kemudian optimal di antara strategi murni dengan kriteria Bayes mengenai risiko adalah strategi $$$u_ {opt}$ memiliki inefisiensi minimal, yaitu risiko rata-rata minimal. Kriteria Bayesian setara dengan sehubungan dengan keuntungan dan relatif terhadap risiko, yaitu jika strateginya $$$u_ {opt}$ optimal dengan kriteria Bayes berkenaan dengan menang, maka optimal dengan kriteria Bayes sehubungan dengan risiko, dan sebaliknya.

Mari kita beralih ke contoh dan menghitung ekspektasi matematis:

$$

$$M_1 = 0 \ cdot0.2 +2 \ cdot0.5 +5 \ cdot0.3 = 2.5; \\ M_2 = 2 \ cdot0.2 +3 \ cdot0.5 +1 \ cdot0.3 = 2.2 ; \\ M_4 = 0 \ cdot0.2 +3 \ cdot0.5 + (- 1) \ cdot0.3 = 2.0;$$

Harapan matematika maksimum adalah $$$M_1$ oleh karena itu, strategi kemenangan adalah strategi $$$U_1$ .

Implementasi perangkat lunak kriteria Bayes:

 class BayesCriteria(gameMatrix: ProbabilityGameMatrix) : ICriteria { val gameMatrix: ProbabilityGameMatrix init { this.gameMatrix = gameMatrix } fun ProbabilityGameMatrix.bayesProbability(): List<Pair<GameVector, Double?>> { var am: MutableList<Pair<GameVector, Double>> = mutableListOf() for (a in this.alternatives) { var alprob: Double = 0.0 for (i in 0..a.values.lastIndex) { alprob += a.values[i] * this.probabilities[i] } am.add(Pair(a, alprob)) } return am.toList(); } override fun optimum(): List<GameVector> { val risk = gameMatrix.bayesProbability() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } } 

Kriteria Laplace

Kriteria Laplace menyajikan maksimalisasi sederhana dari ekspektasi matematis utilitas ketika asumsi probabilitas tingkat permintaan yang sama valid, yang menghilangkan kebutuhan untuk mengumpulkan statistik nyata.

Secara umum, ketika menggunakan kriteria Laplace, matriks utilitas yang diharapkan dan kriteria optimal ditentukan sebagai berikut:

$$

$$u_ {opt} = maks [\ overline {U}] \\ \ overline {U} = \ begin {bmatrix} \ overline {u} _ {1} \\ \ overline {u} _ {2} \\. .. \\ \ overline {u} _ {n} \ end {bmatrix}, \ overline {u} _ {i} = \ frac {1} {n} \ sum_ {j = 1} ^ nu_ {i, j }$$

Pertimbangkan contoh pengambilan keputusan berdasarkan kriteria Laplace. Kami menghitung rata-rata aritmatika untuk setiap strategi:

$$

$$\ overline {u} _ {1} = \ frac {1} {3} \ cdot (0 + 2 + 5) = 2.3 \\ \ overline {u} _ {2} = \ frac {1} { 3} \ cdot (2 + 3 + 1) = 2.0 \\ \ overline {u} _ {3} = \ frac {1} {3} \ cdot (4 + 3-1) = $ 2.$$

Jadi strategi yang menang adalah strategi $$$U_1$ .

Implementasi perangkat lunak dari kriteria Laplace:

 class LaplaceCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.arithemicMean(): List<Pair<GameVector, Double>> { return this.alternatives.map { m -> Pair(m, m.values.average()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.arithemicMean() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second.compareTo(o2.second) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } } 

Strategi campuran. Metode analitik

Metode analitis memungkinkan Anda untuk menyelesaikan permainan dalam berbagai strategi.Untuk merumuskan algoritma untuk menemukan solusi untuk permainan dengan metode analitis, kami mempertimbangkan beberapa konsep tambahan.

Strategi$$U i strategi didominasi$U_{i}$$$U i - 1 , jika semuanya$U_{i-1}$$$$u_{1..n} \in U_{i} \geq u_{1..n} \in U_{i-1}$ .Dengan kata lain, jika dalam satu baris matriks pembayaran semua elemen lebih besar atau sama dengan elemen yang sesuai dari baris lain, maka baris pertama mendominasi yang kedua dan disebut baris dominan. Dan juga jika dalam beberapa kolom matriks pembayaran semua elemen kurang dari atau sama dengan elemen yang sesuai dari kolom lain, maka kolom pertama mendominasi yang kedua dan disebut kolom dominan.

Harga terendah dari gim ini disebut$$$\alpha = max_i min_j u_{ij}$ .
Harga teratas permainan disebut $$$\beta = min_j max_i u_{ij}$ .

Sekarang Anda dapat merumuskan algoritma untuk menyelesaikan permainan dengan metode analitis:

1. Hitung bagian bawah $$α dan atas$\alpha$$$harga game β . Jika$\beta$$$α = β , kemudian tuliskan jawabannya dalam strategi murni, jika tidak, lanjutkan solusinya$\alpha = \beta$
2. Hapus baris dominan kolom. Mungkin ada beberapa. Di tempat mereka dalam strategi optimal, komponen yang sesuai adalah 0
3. Pecahkan permainan matriks dengan pemrograman linier.

Untuk memberikan contoh, Anda perlu memberikan kelas yang menjelaskan solusinya


Dan kelas yang melakukan solusi dengan metode simpleks. Karena saya tidak mengerti matematika, saya menggunakan implementasi yang sudah jadi dari Apache Commons Math


Sekarang kami menjalankan solusi dengan metode analitis. Untuk kejelasan, kami mengambil matriks game lain:

$$

$$\begin{pmatrix} 2& 4& 8& 5 \\ 6& 2& 4& 6\\ 3& 2& 5& 4 \end{pmatrix}$$

Ada set dominan dalam matriks ini:
$$\begin{pmatrix} 2& 4\\ 6& 2\end{pmatrix}$$

Solusi permainan $$( 0 , 33 ; 0 , 67 ; 0 ) dengan harga permainan sama dengan 3,33$(0,33; 0,67; 0)$

Alih-alih sebuah kesimpulan

Saya harap artikel ini akan bermanfaat bagi mereka yang membutuhkan pendekatan pertama dengan solusi game dengan alam. Alih-alih kesimpulan, tautan ke GitHub .

Saya akan berterima kasih atas umpan balik yang membangun!