Halo, Habr! Saya mempersembahkan bagi Anda halaman depan Solving bandit multiarmed: Sebuah perbandingan artikel sampel epsilon-serakah dan Thompson .

Masalah bandit multi-bersenjata

Masalah bandit multi-bersenjata adalah salah satu tugas paling dasar dalam ilmu solusi. Yaitu, ini adalah masalah alokasi sumber daya yang optimal dalam kondisi ketidakpastian. Nama "multi-bersenjata bandit" sendiri berasal dari mesin slot lama yang dikendalikan oleh pegangan. Senapan serbu ini dijuluki "bandit," karena setelah berbicara dengan mereka, orang biasanya merasa dirampok. Sekarang bayangkan ada beberapa mesin seperti itu dan peluang untuk menang melawan mobil yang berbeda berbeda. Karena kami mulai bermain dengan mesin ini, kami ingin menentukan peluang mana yang lebih tinggi dan menggunakan mesin ini lebih sering daripada yang lain.

Masalahnya adalah ini: bagaimana kita paling efisien memahami mesin mana yang paling cocok, dan pada saat yang sama mencoba banyak fitur secara real time? Ini bukan semacam masalah teoretis, ini adalah masalah yang dihadapi bisnis setiap saat. Misalnya, perusahaan memiliki beberapa opsi untuk pesan yang perlu diperlihatkan kepada pengguna (misalnya, pesan menyertakan iklan, situs, gambar) sehingga pesan yang dipilih memaksimalkan tugas bisnis tertentu (konversi, klik, dll.)

Cara khas untuk mengatasi masalah ini adalah dengan menjalankan tes A / B berkali-kali. Yaitu, selama beberapa minggu untuk menunjukkan masing-masing opsi secara merata, dan kemudian, berdasarkan uji statistik, tentukan pilihan mana yang lebih baik. Metode ini cocok ketika ada beberapa opsi, katakanlah, 2 atau 4. Tetapi ketika ada banyak opsi, pendekatan ini menjadi tidak efektif - baik dalam waktu yang hilang maupun laba yang hilang.

Dari mana waktu yang hilang berasal harus mudah dimengerti. Lebih banyak opsi - lebih banyak tes A / B dibutuhkan - lebih banyak waktu diperlukan untuk membuat keputusan. Terjadinya laba yang hilang tidak begitu jelas. Kehilangan peluang (opportunity cost) - biaya yang terkait dengan fakta bahwa alih-alih satu tindakan kami melakukan yang lain, yaitu, secara sederhana, inilah yang kami hilangkan dengan berinvestasi di A, bukannya B. Berinvestasi dalam B adalah laba yang hilang dari investasi di A. Sama dengan opsi memeriksa. Tes A / B tidak boleh diganggu sampai selesai. Ini berarti bahwa eksperimen tidak tahu opsi mana yang lebih baik sampai pengujian selesai. Namun, masih diyakini bahwa satu opsi akan lebih baik daripada yang lain. Ini berarti bahwa dengan memperpanjang tes A / B, kami tidak menunjukkan opsi terbaik untuk jumlah pengunjung yang cukup besar (meskipun kami tidak tahu opsi mana yang bukan yang terbaik), sehingga kehilangan keuntungan kami. Ini adalah manfaat yang hilang dari pengujian A / B. Jika hanya ada satu tes A / B, maka mungkin untung yang hilang sama sekali tidak bagus. Sejumlah besar tes A / B berarti bahwa untuk waktu yang lama kami harus menunjukkan kepada pelanggan banyak pilihan bukan yang terbaik. Akan lebih baik jika Anda dapat dengan cepat membuang opsi yang buruk secara real time, dan hanya kemudian, ketika ada beberapa pilihan yang tersisa, gunakan tes A / B untuk mereka.

Pengambil sampel atau agen adalah cara untuk menguji dan mengoptimalkan distribusi opsi dengan cepat. Pada artikel ini, saya akan memperkenalkan Anda pada pengambilan sampel Thompson dan propertinya. Saya juga akan membandingkan pengambilan sampel Thompson dengan algoritma epsilon-serakah, pilihan populer lainnya untuk masalah bandit multi-bersenjata. Semuanya akan diimplementasikan dalam Python dari awal - semua kode dapat ditemukan di sini .

Kamus Singkat Konsep

Agent, sampler, bandit ( agent, sampler, bandit ) - sebuah algoritma yang membuat keputusan tentang opsi mana yang akan ditampilkan.
Varian - varian berbeda dari pesan yang dilihat pengunjung.
Tindakan - tindakan yang dipilih algoritma (opsi untuk ditampilkan).
Gunakan ( exploit ) - buat pilihan untuk memaksimalkan total hadiah berdasarkan data yang tersedia.
Jelajahi, jelajahi - buat pilihan untuk lebih memahami pengembalian untuk setiap opsi.
Penghargaan, poin ( skor, hadiah ) - tugas bisnis, misalnya konversi atau clickability. Untuk kesederhanaan, kami percaya bahwa itu didistribusikan secara biner dan sama dengan 1 atau 0 - diklik atau tidak.
Lingkungan - konteks di mana agen beroperasi - opsi dan "pengembalian" tersembunyi untuk pengguna.
Payback, probabilitas keberhasilan ( payout rate ) - variabel tersembunyi sama dengan probabilitas mendapatkan skor = 1, untuk setiap opsi berbeda. Tetapi pengguna tidak melihatnya.
Coba ( uji coba ) - pengguna mengunjungi halaman.
Penyesalan adalah perbedaan antara apa yang akan menjadi hasil terbaik dari semua opsi yang tersedia dan apa hasil dari opsi yang tersedia dalam upaya saat ini. Semakin menyesali tindakan yang sudah dilakukan, semakin baik.
Pesan ( pesan ) - spanduk, opsi halaman, dan banyak lagi, versi berbeda yang ingin kami coba.
Sampling - pembuatan sampel dari distribusi yang diberikan.

Jelajahi dan eksploitasi

Agen adalah algoritma yang mencari pendekatan untuk pengambilan keputusan real-time untuk mencapai keseimbangan antara menjelajahi ruang opsi dan menggunakan opsi terbaik. Keseimbangan ini sangat penting. Ruang opsi harus diselidiki untuk memiliki gagasan tentang opsi mana yang terbaik. Jika kami pertama kali menemukan opsi yang paling optimal ini, dan kemudian menggunakannya sepanjang waktu, kami akan memaksimalkan total hadiah yang tersedia bagi kami dari lingkungan. Di sisi lain, kami juga ingin menjelajahi opsi lain yang mungkin - bagaimana jika mereka akan berubah menjadi lebih baik di masa depan, tetapi kami belum tahu? Dengan kata lain, kami ingin memastikan kemungkinan kerugian, mencoba bereksperimen sedikit dengan opsi suboptimal untuk mengklarifikasi sendiri pengembalian mereka. Jika pengembalian mereka sebenarnya lebih tinggi, mereka dapat ditampilkan lebih sering. Kelebihan lainnya dari meneliti opsi adalah bahwa kita dapat lebih memahami tidak hanya pengembalian rata-rata, tetapi juga bagaimana kira-kira pembayaran dikembalikan, yaitu kita dapat memperkirakan ketidakpastian dengan lebih baik.
Masalah utama, oleh karena itu, adalah untuk memecahkan - apa jalan keluar terbaik dari dilema antara eksplorasi dan eksploitasi (tradeoff eksplorasi-eksploitasi).

Algoritma Epsilon-serakah

Jalan keluar khas dari dilema ini adalah algoritma epsilon-serakah. "Serakah" berarti apa yang Anda pikirkan. Setelah beberapa periode awal, ketika kita secara tidak sengaja melakukan upaya - katakan, 1000 kali, algoritme dengan penuh semangat memilih opsi terbaik k dalam setiap persen upaya. Misalnya, jika e = 0,05, algoritma 95% dari waktu memilih opsi terbaik, dan sisanya 5% dari waktu itu memilih upaya acak. Sebenarnya, ini adalah algoritma yang agak efektif, namun, mungkin tidak cukup untuk menjelajahi ruang pilihan, dan oleh karena itu, tidak akan cukup baik untuk mengevaluasi opsi mana yang terbaik, untuk terjebak pada opsi yang kurang optimal. Mari kita tunjukkan dalam kode bagaimana algoritma ini bekerja.

Tapi pertama-tama, beberapa ketergantungan. Kita harus mendefinisikan lingkungan. Ini adalah konteks di mana algoritma akan berjalan. Dalam hal ini, konteksnya sangat sederhana. Dia memanggil agen sehingga agen memutuskan tindakan mana yang harus dipilih, kemudian konteks meluncurkan tindakan ini dan mengembalikan poin yang diterima untuk kembali ke agen (yang entah bagaimana memperbarui keadaannya).

class Environment: def __init__(self, variants, payouts, n_trials, variance=False): self.variants = variants if variance: self.payouts = np.clip(payouts + np.random.normal(0, 0.04, size=len(variants)), 0, .2) else: self.payouts = payouts #self.payouts[5] = self.payouts[5] if i < n_trials/2 else 0.1 self.n_trials = n_trials self.total_reward = 0 self.n_k = len(variants) self.shape = (self.n_k, n_trials) def run(self, agent): """Run the simulation with the agent. agent must be a class with choose_k and update methods.""" for i in range(self.n_trials): # agent makes a choice x_chosen = agent.choose_k() # Environment returns reward reward = np.random.binomial(1, p=self.payouts[x_chosen]) # agent learns of reward agent.reward = reward # agent updates parameters based on the data agent.update() self.total_reward += reward agent.collect_data() return self.total_reward

Poin didistribusikan secara biner dengan probabilitas p tergantung pada jumlah tindakan (sama seperti mereka dapat didistribusikan terus menerus, esensi tidak akan berubah). Saya juga akan mendefinisikan kelas BaseSampler - diperlukan hanya untuk menyimpan log dan berbagai atribut.

 class BaseSampler: def __init__(self, env, n_samples=None, n_learning=None, e=0.05): self.env = env self.shape = (env.n_k, n_samples) self.variants = env.variants self.n_trials = env.n_trials self.payouts = env.payouts self.ad_i = np.zeros(env.n_trials) self.r_i = np.zeros(env.n_trials) self.thetas = np.zeros(self.n_trials) self.regret_i = np.zeros(env.n_trials) self.thetaregret = np.zeros(self.n_trials) self.a = np.ones(env.n_k) self.b = np.ones(env.n_k) self.theta = np.zeros(env.n_k) self.data = None self.reward = 0 self.total_reward = 0 self.k = 0 self.i = 0 self.n_samples = n_samples self.n_learning = n_learning self.e = e self.ep = np.random.uniform(0, 1, size=env.n_trials) self.exploit = (1 - e) def collect_data(self): self.data = pd.DataFrame(dict(ad=self.ad_i, reward=self.r_i, regret=self.regret_i))

Di bawah ini kami menetapkan 10 opsi dan pembayaran untuk masing-masing. Opsi terbaik adalah opsi 9 dengan pengembalian 0,11%.

 variants = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] payouts = [0.023, 0.03, 0.029, 0.001, 0.05, 0.06, 0.0234, 0.035, 0.01, 0.11]

Untuk membangun sesuatu, kami juga mendefinisikan kelas RandomSampler. Kelas ini diperlukan sebagai model dasar. Dia hanya secara acak memilih opsi pada setiap upaya dan tidak memperbarui parameternya.

 class RandomSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): self.k = np.random.choice(self.variants) return self.k def update(self): # nothing to update #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.thetaregret) - self.theta[self.k] #self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.theta) - self.theta[self.k] self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

Model-model lain memiliki struktur sebagai berikut. Semua memiliki select_k dan memperbarui metode. select_k mengimplementasikan metode dimana agen memilih opsi. perbarui memperbarui parameter agen - metode ini mencirikan bagaimana kemampuan agen untuk memilih perubahan opsi (dengan RandomSampler kemampuan ini tidak berubah dengan cara apa pun). Kami menjalankan agen di lingkungan menggunakan pola berikut.

 en0 = Environment(machines, payouts, n_trials=10000) rs = RandomSampler(env=en0) en0.run(agent=rs)

Inti dari algoritma epsilon-serakah adalah sebagai berikut.

Pilih secara acak k untuk n percobaan.
Pada setiap percobaan, untuk setiap opsi, evaluasi keuntungan.
Setelah semua n upaya:
Dengan probabilitas 1 - e pilih k dengan gain tertinggi;
Dengan probabilitas e pilih K secara acak.

Kode Epsilon-serakah:

 class eGreedy(BaseSampler): def __init__(self, env, n_learning, e): super().__init__(env, n_learning, e) def choose_k(self): # e% of the time take a random draw from machines # random k for n learning trials, then the machine with highest theta self.k = np.random.choice(self.variants) if self.i < self.n_learning else np.argmax(self.theta) # with 1 - e probability take a random sample (explore) otherwise exploit self.k = np.random.choice(self.variants) if self.ep[self.i] > self.exploit else self.k return self.k # every 100 trials update the successes # update the count of successes for the chosen machine def update(self): # update the probability of payout for each machine self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b #self.total_reward += self.reward #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] #self.thetaregret[self.i] = self.thetaregret[self.i] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

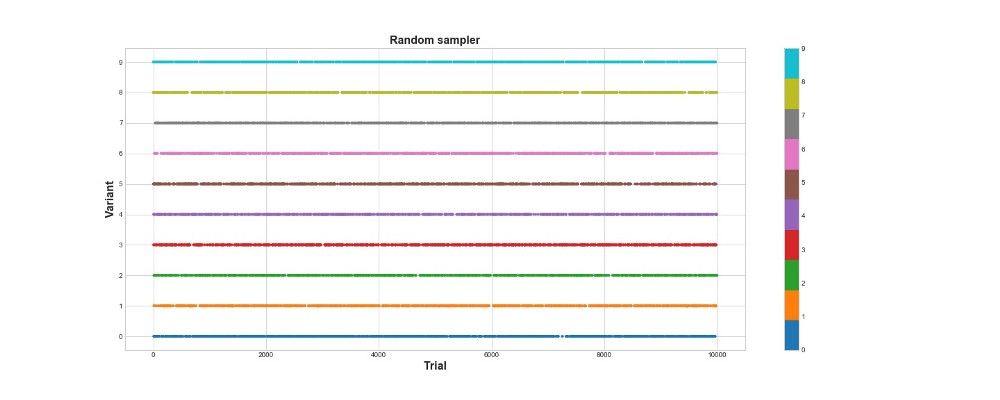
Di bawah ini pada grafik, Anda dapat melihat hasil dari sampel acak murni, yaitu, dengan kata lain, tidak ada model di sini. Grafik menunjukkan pilihan algoritma yang dibuat pada setiap upaya, jika ada 10 ribu upaya. Algoritma hanya mencoba, tetapi tidak belajar. Secara total, ia mencetak 418 poin.

Mari kita lihat bagaimana algoritma epsilon-serakah berperilaku di lingkungan yang sama. Jalankan algoritme untuk 10 ribu upaya dengan e = 0,1 dan n_learning = 500 (agen cukup mencoba 500 upaya pertama, kemudian mencoba dengan probabilitas e = 0,1). Mari kita evaluasi algoritme berdasarkan jumlah total poin yang dihasilkannya dalam lingkungan.

 en1 = Environment(machines, payouts, n_trials) eg = eGreedy(env=en1, n_learning=500, e=0.1) en1.run(agent=eg)

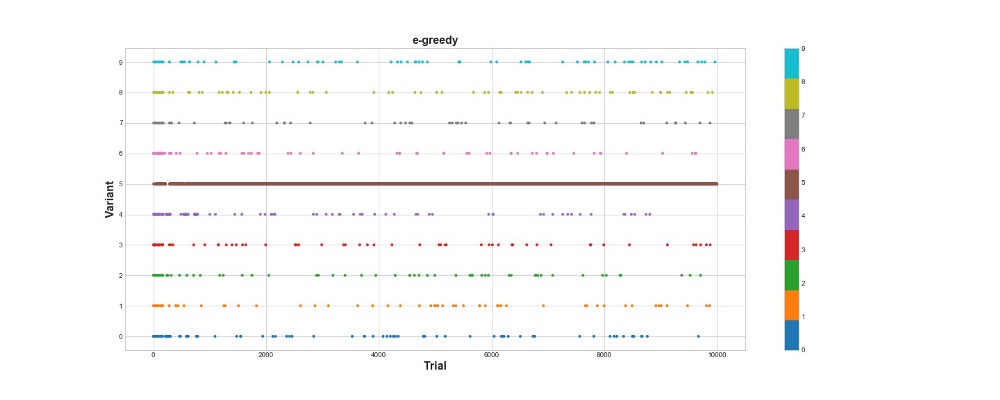
Algoritma Epsilon-serakah mencetak 788 poin, hampir 2 kali lebih baik daripada algoritma acak - super! Grafik kedua menjelaskan algoritma ini dengan cukup baik. Kita melihat bahwa untuk 500 langkah pertama aksi didistribusikan secara merata dan K dipilih secara acak. Namun, kemudian mulai sangat mengeksploitasi opsi 5 - ini adalah opsi yang cukup kuat, tetapi bukan yang terbaik. Kami juga melihat bahwa agen masih secara acak memilih 10% dari waktu.

Ini cukup keren - kami hanya menulis beberapa baris kode, dan sekarang kami sudah memiliki algoritma yang cukup kuat yang dapat menjelajahi ruang pilihan dan membuat keputusan yang mendekati optimal. Di sisi lain, algoritma tidak menemukan opsi terbaik. Ya, kami dapat meningkatkan jumlah langkah untuk belajar, tetapi dengan cara ini kami akan menghabiskan lebih banyak waktu untuk pencarian acak, semakin memperburuk hasil akhir. Juga, keacakan dijahit ke dalam proses ini secara default - algoritma terbaik mungkin tidak ditemukan.

Nanti saya akan menjalankan masing-masing algoritma berkali-kali sehingga kita dapat membandingkannya relatif satu sama lain. Tetapi untuk sekarang, mari kita lihat pengambilan sampel Thompson dan mengujinya di lingkungan yang sama.

Sampling Thompson

Sampling Thompson pada dasarnya berbeda dari algoritma epsilon-serakah oleh tiga poin utama:

Itu tidak serakah.
Itu membuat upaya dengan cara yang lebih canggih.
Itu adalah Bayesian.

Poin utamanya adalah paragraf 3, paragraf 1 dan 2 ikuti darinya.

Inti dari algoritma ini adalah:

Tetapkan distribusi beta awal antara 0 dan 1 untuk pengembalian setiap opsi.
Cicipi pilihan dari distribusi ini, pilih parameter Theta maksimum.
Pilih opsi k yang dikaitkan dengan theta terbesar.
Lihat berapa banyak poin yang telah dicetak, perbarui parameter distribusi.

Baca lebih lanjut tentang distribusi beta di sini .
Dan tentang penggunaannya dalam Python - di sini .

Kode Algoritma:

  class ThompsonSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): # sample from posterior (this is the thompson sampling approach) # this leads to more exploration because machines with > uncertainty can then be selected as the machine self.theta = np.random.beta(self.a, self.b) # select machine with highest posterior p of payout self.k = self.variants[np.argmax(self.theta)] #self.k = np.argmax(self.a/(self.a + self.b)) return self.k def update(self): #update dist (a, b) = (a, b) + (r, 1 - r) self.a[self.k] += self.reward self.b[self.k] += 1 - self.reward # ie only increment b when it's a swing and a miss. 1 - 0 = 1, 1 - 1 = 0 #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

Notasi formal dari algoritma terlihat seperti ini.

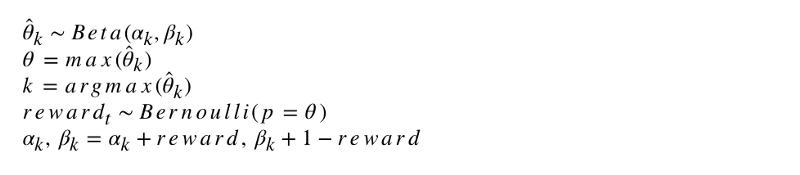
Mari kita programkan algoritma ini. Seperti agen lainnya, ThompsonSampler mewarisi dari BaseSampler dan menentukan select_k dan memperbarui metode sendiri. Sekarang luncurkan agen baru kami.

  en2 = Environment(machines, payouts, n_trials) tsa = ThompsonSampler(env=en2) en2.run(agent=tsa)

Seperti yang Anda lihat, dia mencetak lebih dari algoritma epsilon-serakah. Hebat! Mari kita lihat grafik pemilihan usaha. Dua hal menarik terlihat di sana. Pertama, agen dengan benar menemukan opsi terbaik (opsi 9) dan menggunakannya secara maksimal. Kedua, agen menggunakan opsi lain, tetapi dengan cara yang lebih sulit - setelah sekitar 1000 upaya, agen, selain opsi utama, terutama menggunakan opsi yang paling kuat di antara yang lain. Dengan kata lain, dia tidak memilih secara acak, tetapi lebih kompeten.

Mengapa ini bekerja? Sederhana - ketidakpastian dalam distribusi posterior dari manfaat yang diharapkan untuk setiap opsi berarti bahwa setiap opsi dipilih dengan probabilitas yang kira-kira sebanding dengan bentuknya, ditentukan oleh parameter alfa dan beta. Dengan kata lain, pada setiap percobaan, pengambilan sampel Thompson memicu pilihan sesuai dengan probabilitas posterior bahwa itu memiliki manfaat maksimal. Secara kasar, setelah dari informasi distribusi tentang ketidakpastian, agen memutuskan kapan untuk memeriksa lingkungan dan kapan menggunakan informasi tersebut. Sebagai contoh, opsi lemah dengan ketidakpastian posterior tinggi mungkin membayar paling untuk upaya ini. Tetapi untuk sebagian besar upaya, semakin kuat distribusi posteriornya, semakin besar rata-rata dan semakin sedikit standar deviasinya, dan karenanya, semakin besar peluang untuk memilihnya.

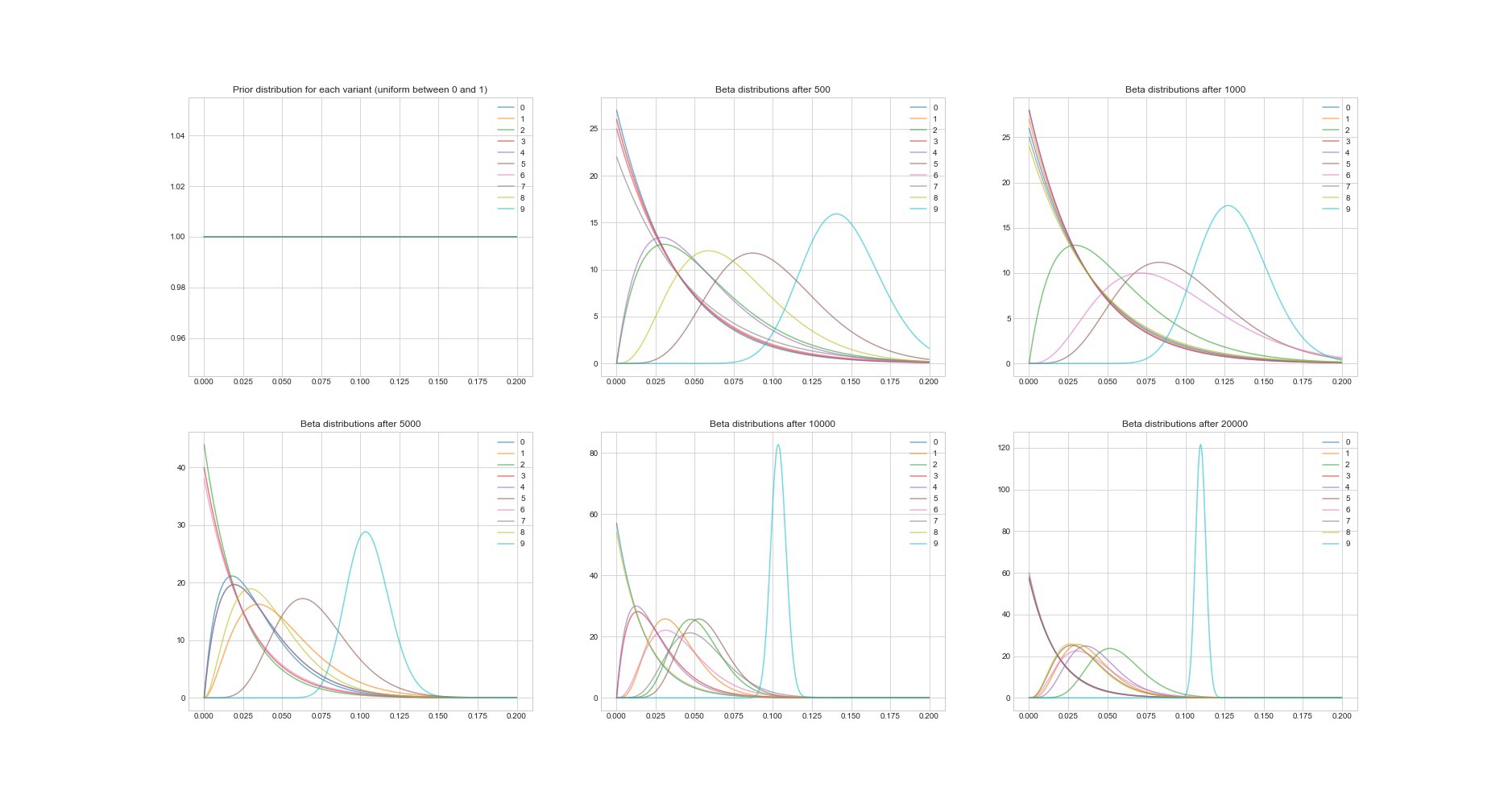
Properti luar biasa lainnya dari algoritma Thompson: karena ini adalah Bayesian, kita dapat memperkirakan ketidakpastian dalam estimasi pengembalian untuk setiap opsi menggunakan parameternya. Grafik di bawah ini menunjukkan distribusi posterior pada 6 titik berbeda dan dalam 20.000 upaya. Anda melihat bagaimana distribusi secara bertahap mulai menyatu dengan opsi dengan pengembalian terbaik.

Sekarang bandingkan ketiga agen dalam 100 simulasi. 1 simulasi adalah peluncuran agen pada 10.000 upaya.

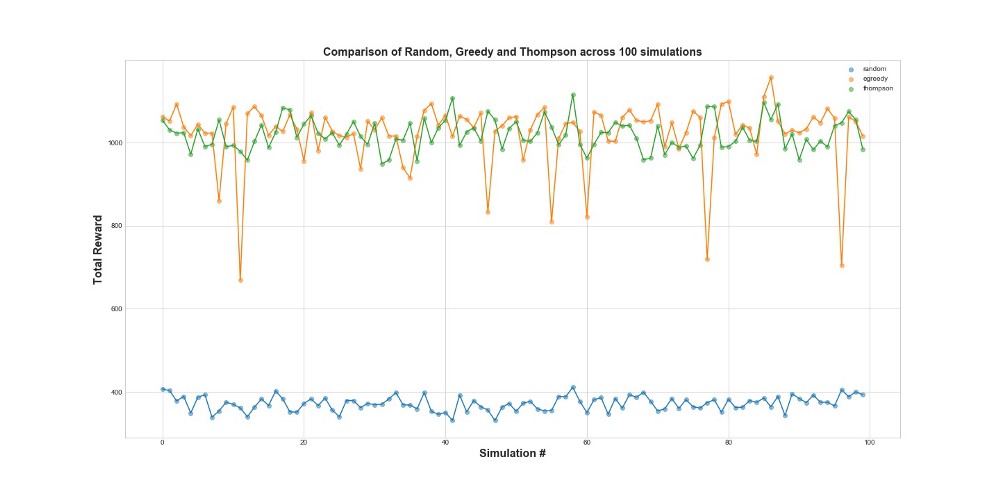
Seperti yang dapat Anda lihat dari grafik, baik strategi epsilon-serakah dan pengambilan sampel Thompson jauh lebih baik daripada pengambilan sampel acak. Anda mungkin terkejut bahwa strategi epsilon-serakah dan pengambilan sampel Thompson sebenarnya sebanding dalam hal kinerja mereka. Strategi Epsilon-serakah bisa sangat efektif, tetapi lebih berisiko, karena bisa terjebak pada opsi suboptimal - ini dapat dilihat pada kegagalan dalam grafik. Tapi pengambilan sampel Thompson tidak bisa, karena itu membuat pilihan dalam ruang pilihan dengan cara yang lebih kompleks.

Menyesal

Cara lain untuk mengevaluasi seberapa baik algoritma bekerja adalah untuk mengevaluasi penyesalan. Secara kasar, semakin kecil, dalam kaitannya dengan tindakan yang telah diambil, semakin baik. Di bawah ini adalah grafik dari total penyesalan dan penyesalan atas kesalahan. Sekali lagi - semakin sedikit penyesalan, semakin baik.

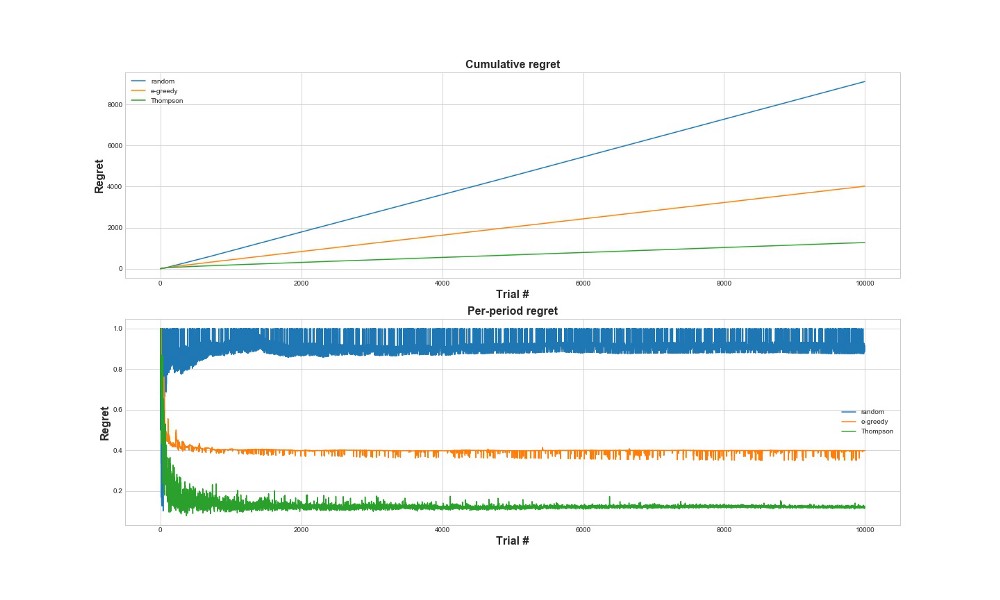
Pada grafik atas, kita melihat penyesalan total, dan pada penyesalan yang lebih rendah upaya. Seperti dapat dilihat dari grafik, sampling Thompson konvergen ke penyesalan minimal jauh lebih cepat daripada strategi epsilon-serakah. Dan itu konvergen ke level yang lebih rendah. Dengan pengambilan sampel Thompson, agen tersebut menyesal lebih sedikit karena ia dapat lebih baik mendeteksi opsi terbaik dan mencoba opsi yang paling menjanjikan dengan lebih baik - sehingga pengambilan sampel Thompson sangat cocok untuk kasus penggunaan yang lebih maju, seperti model statistik atau jaringan saraf untuk memilih k.

Kesimpulan

Ini adalah posting teknis yang cukup panjang. Sebagai rangkuman, kita dapat menggunakan metode pengambilan sampel yang cukup canggih jika kita memiliki banyak opsi yang ingin kita uji secara real time. Salah satu fitur yang sangat baik dari pengambilan sampel Thompson adalah menyeimbangkan penggunaan dan eksplorasi dengan cara yang agak rumit. Artinya, kita bisa membiarkannya mengoptimalkan distribusi opsi solusi secara real time. Ini adalah algoritma yang keren, dan harus lebih berguna untuk bisnis daripada tes A / B.

Penting! Sampling Thompson tidak berarti Anda tidak perlu melakukan tes A / B. Biasanya, mereka pertama kali menemukan opsi terbaik dengan bantuannya, dan kemudian melakukan tes A / B pada mereka.

Masalah Bandit Multi-Senjata - Bandingkan Strategi Epsilon-Greedy dan Thompson Sampling