👨‍🏫 🔀 🔚 Solusi simbolik dari persamaan diferensial linear dan sistem dengan metode transformasi Laplace menggunakan SymPy 👩🏿‍🤝‍👨🏽 👨🏾‍🎤 👩🏽‍🏭

Implementasi algoritma dalam Python menggunakan perhitungan simbolik sangat nyaman untuk memecahkan masalah pemodelan matematika objek yang didefinisikan oleh persamaan diferensial. Untuk menyelesaikan persamaan tersebut, Transformasi Laplace banyak digunakan, yang, dalam istilah yang disederhanakan, memungkinkan untuk mengurangi masalah untuk menyelesaikan persamaan aljabar sederhana.

Dalam publikasi ini, saya mengusulkan untuk mempertimbangkan fungsi transformasi Laplace langsung dan terbalik dari perpustakaan SymPy, yang memungkinkan Anda untuk menggunakan metode Laplace untuk menyelesaikan persamaan diferensial dan sistem menggunakan Python.

Metode Laplace itu sendiri dan keuntungannya dalam menyelesaikan persamaan dan sistem diferensial linear secara luas dibahas dalam literatur, misalnya, dalam publikasi populer [1]. Dalam buku ini, metode Laplace disajikan untuk implementasi dalam paket perangkat lunak berlisensi Mathematica, Maple dan MATLAB (yang menyiratkan pembelian perangkat lunak ini oleh lembaga pendidikan) menggunakan contoh-contoh yang dipilih oleh penulis.

Hari ini kami akan mencoba untuk mempertimbangkan bukan contoh terpisah untuk memecahkan masalah pembelajaran menggunakan Python, tetapi metode umum untuk menyelesaikan persamaan dan sistem diferensial linear menggunakan fungsi transformasi Laplace langsung dan terbalik. Pada saat yang sama, kita akan menghemat momen pembelajaran: sisi kiri persamaan diferensial linier dengan kondisi Cauchy akan dibentuk oleh siswa sendiri, dan bagian rutin dari tugas, yang terdiri dari transformasi Laplace langsung dari sisi kanan persamaan, akan dilakukan menggunakan fungsi laplace_transform () .

Kisah kepenulisan Laplace berubah

Transformasi Laplace (gambar Laplace) memiliki riwayat yang menarik. Untuk pertama kalinya, integral dalam definisi transformasi Laplace muncul dalam salah satu karya L. Euler. Namun, umumnya diterima dalam matematika untuk memanggil metodologi atau teorema nama ahli matematika yang menemukannya setelah Euler. Kalau tidak, akan ada beberapa ratus teorema Euler yang berbeda.

Dalam kasus ini, Euler berikutnya adalah ahli matematika Prancis Pierre Simon de Laplace (Pierre Simon de Laplace (1749-1827)). Dialah yang menggunakan integral seperti itu dalam karyanya pada teori probabilitas. Laplace sendiri tidak menerapkan apa yang disebut "metode operasional" untuk menemukan solusi persamaan diferensial berdasarkan transformasi Laplace (gambar Laplace). Metode ini sebenarnya ditemukan dan dipopulerkan oleh insinyur praktis, terutama insinyur listrik Inggris Oliver Heaviside (1850-1925). Jauh sebelum validitas metode-metode ini dibuktikan dengan teliti, kalkulus operasional telah berhasil dan digunakan secara luas, meskipun legitimasinya dipertanyakan sebagian besar bahkan pada awal abad ke-20, dan ada perdebatan yang sangat sengit mengenai topik ini.

Fungsi transformasi Laplace langsung dan terbalik

Fungsi Transformasi Langsung Laplace:
sympy.integrals.transforms. laplace_transform (t, s, ** hints).
Fungsi laplace_transform () melakukan transformasi Laplace dari fungsi f (t) dari variabel real ke dalam fungsi F (s) dari variabel kompleks, sehingga:
$F (s) = \ int_ {0} ^ {∞} f (t) e ^ {- st} dt.$

Fungsi ini mengembalikan (F, a, cond) , di mana F (s) adalah Transformasi Laplace dari fungsi f (t) , a <Re (s) adalah setengah-bidang di mana F (s) didefinisikan, dan cond adalah kondisi tambahan untuk konvergensi integral.
Jika integral tidak dapat dihitung dalam bentuk tertutup, fungsi ini mengembalikan objek LaplaceTransform yang tidak dikomputasi .
Jika Anda mengatur opsi noconds = True , fungsi hanya mengembalikan F (s) .
Fungsi transformasi Laplace terbalik:

sympy.integrals.transforms. inverse_laplace_transform (F, s, t, plane = Tidak ada, petunjuk **).

Fungsi inverse_laplace_transform () melakukan transformasi Laplace terbalik dari fungsi variabel kompleks F (s) ke dalam fungsi f (t) dari variabel nyata, sehingga:
$f (t) = \ frac {1} {2 \ pi i} \ int_ {c-∞ \ cdot i} ^ {c + ∞ \ cdot i} e ^ {st} F (s) ds$

Jika integral tidak dapat dihitung dalam bentuk tertutup, fungsi ini mengembalikan objek InverseLaplaceTransform yang tidak dikomputasi .

Transformasi Laplace terbalik pada contoh menentukan karakteristik transisi dari regulator

Fungsi transfer pengontrol PID memiliki bentuk [2]:

$W (s) = (1+ \ frac {K_ {d} \ cdot T_ {d} \ cdot s} {1 + T_ {d} \ cdot s}) \ cdot K_ {p} \ cdot (1+ \ frac {1} {T_ {i} \ cdot s}) \ cdot \ frac {1} {s}.$

Kami akan menulis sebuah program untuk mendapatkan persamaan untuk karakteristik transien dari pengontrol PID dan PI untuk fungsi transfer yang dikurangi, dan juga menambah waktu yang dihabiskan untuk transformasi Laplace visual terbalik.

Teks program

#   : from sympy import * import time import matplotlib.pyplot as plt import numpy as np start = time.time() #   : var('s Kp Ti Kd Td') #      : var('t', positive=True) Kp = 2 Ti = 2 Kd = 4 Td = Rational(1, 2) #   -   s: fp = (1 + (Kd * Td * s) / (1 + Td*s)) * Kp * (1 + 1/(Ti*s)) * (1/s) #   -, #     : ht = inverse_laplace_transform(fp, s, t) Kd = 0 #   - (Kd = 0)   s: fpp = (1 + (Kd * Td * s) / (1 + Td*s)) * Kp * (1 + 1/(Ti*s)) * (1/s) #   -, #     : htt = inverse_laplace_transform(fpp, s, t) stop = time.time() print ('     : %ss' % N((stop-start), 3)) #      : f = lambdify(t, ht, 'numpy') F = lambdify(t, htt, 'numpy') tt = np.arange(0.01, 20, 0.05) #  : plt.title('   \n   : \n  - W(s)=%s \n  - W(s)=%s' % (fp, fpp)) plt.plot(tt, f(tt), color='r', linewidth=2, label='-: h(t)=%s' % ht) plt.plot(tt, F(tt), color='b', linewidth=2, label='-: h(t)=%s' % htt) plt.grid(True) plt.legend(loc='best') plt.show()

Kami mendapatkan:

Membalikkan Waktu Transformasi Laplace Visual: 2,68 dtk

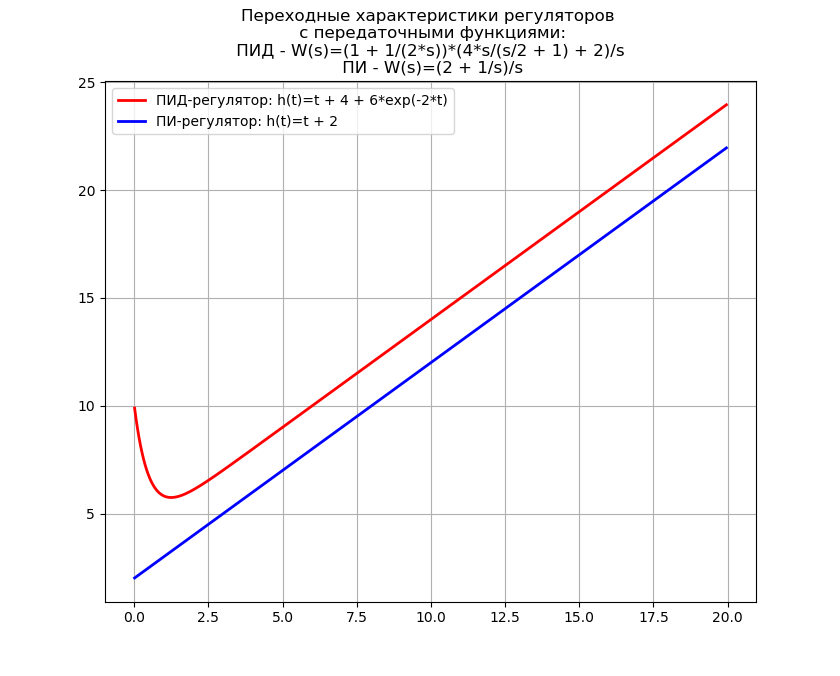
Transformasi invers Laplace sering digunakan dalam sintesis senjata self-propelled, di mana Python dapat menggantikan "monster" perangkat lunak yang mahal seperti MathCAD, sehingga penggunaan invers transform di atas sangat penting secara praktis.

Transformasi Laplace dari turunan dari pesanan yang lebih tinggi untuk menyelesaikan masalah Cauchy

Diskusi kami akan melanjutkan dengan penerapan transformasi Laplace (gambar Laplace) untuk mencari solusi persamaan diferensial linier dengan koefisien bentuk konstan:

$a \ cdot x '' (t) + b \ cdot x '(t) + c \ cdot x (t) = f (t). (1)$

Jika a dan b adalah konstanta, maka

L \ kiri \ {a \ cdot f (t) + b \ cdot q (t) \ kanan \} = a \ cdot L \ kiri \ {f (t) \ kanan \} + b \ cdot L \ kiri \ {q (t) \ kanan \} (2)

$L \ kiri \ {a \ cdot f (t) + b \ cdot q (t) \ kanan \} = a \ cdot L \ kiri \ {f (t) \ kanan \} + b \ cdot L \ kiri \ {q (t) \ kanan \} (2)$

untuk semua s sehingga Transformasi Laplace (gambar Laplace) dari fungsi f (t) dan q (t) ada.

Mari kita memverifikasi linearitas transformasi Laplace langsung dan terbalik menggunakan fungsi yang sebelumnya dianggap laplace_transform () dan inverse_laplace_transform () . Untuk ini, kita ambil f (t) = sin (3t) , q (t) = cos (7t) , a = 5 , b = 7 sebagai contoh, dan gunakan program berikut.

Teks program

 from sympy import* var('sa b') var('t', positive=True) a = 5 f = sin(3*t) b = 7 q = cos(7*t) #   a*L{f(t)}: L1 = a * laplace_transform(f, t, s, noconds=True) #   b*L{q(t)}: L2 = b*laplace_transform(q, t, s, noconds=True) #  a*L{f(t)}+b*L{q(t)}: L = factor(L1 + L2) print (L) #   L{a*f(t)+b*q(t)}: LS = factor(laplace_transform(a*f + b*q, t, s, noconds=True)) print (LS) print (LS == L) #   a* L^-1{f(t)}: L_1 = a * inverse_laplace_transform(L1/a, s, t) #   b* L^-1{q(t)} L_2 = b * inverse_laplace_transform(L2/b, s, t) # a* L^-1{f(t)}+b* L^-1{q(t)}: L_S = L_1 + L_2 print (L_S) #   L^-1{a*f(t)+b*q(t)}: L_1_2 = inverse_laplace_transform(L1 + L2, s, t) print (L_1_2) print (L_1_2 == L_S)

Kami mendapatkan:

(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
Benar
5 * dosa (3 * t) + 7 * cos (7 * t)
5 * dosa (3 * t) + 7 * cos (7 * t)

Kode di atas juga menunjukkan keunikan dari transformasi Laplace terbalik.

Dengan asumsi itu

$q (t) = f '(t)$ memenuhi syarat-syarat teorema pertama, maka dari teorema ini akan mengikuti bahwa:

L \ kiri \ {f '' (t) \ kanan \} = L \ kiri \ {q '(t) \ kanan \} = sL \ kiri \ {q (t) \ kanan \} - q (0) = sL \ kiri \ {f '(t) \ kanan \} - f' (0) = s \ kiri [sL \ kiri \ {f (t) -f (0) \ kanan \} \ kanan],

$L \ kiri \ {f '' (t) \ kanan \} = L \ kiri \ {q '(t) \ kanan \} = sL \ kiri \ {q (t) \ kanan \} - q (0) = sL \ kiri \ {f '(t) \ kanan \} - f' (0) = s \ kiri [sL \ kiri \ {f (t) -f (0) \ kanan \} \ kanan],$

dan karenanya

L \ kiri \ {f '' (t) \ kanan \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f '(0).

$L \ kiri \ {f '' (t) \ kanan \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f '(0).$

Mengulangi perhitungan ini memberi

L \ kiri \ {f '' '(t) \ kanan \} = sL \ kiri \ {f' '(t) \ kanan \} - f' '(0) = s ^ {3} F (s) -s ^ {2} f (0) -sf '(0) -f' '(0).

$L \ kiri \ {f '' '(t) \ kanan \} = sL \ kiri \ {f' '(t) \ kanan \} - f' '(0) = s ^ {3} F (s) -s ^ {2} f (0) -sf '(0) -f' '(0).$

Setelah sejumlah langkah tersebut, kami memperoleh generalisasi teorema pertama berikut:

L \ kiri \ {f ^ {(n)} (t) \ kanan \} = s ^ {n} L \ kiri \ {f (t) \ kanan \} - s ^ {n-1} f (0 ) -s ^ {n-2} f '(0) - \ cdot \ cdot \ cdot -f ^ {(n-1)} (0) =

$L \ kiri \ {f ^ {(n)} (t) \ kanan \} = s ^ {n} L \ kiri \ {f (t) \ kanan \} - s ^ {n-1} f (0 ) -s ^ {n-2} f '(0) - \ cdot \ cdot \ cdot -f ^ {(n-1)} (0) =$

$= s ^ {n} F (s) -s ^ {n-1} f (0) - \ cdot \ cdot \ cdot -sf ^ {(n-2)} (0) -f ^ {(n- 1)} (0). (3)$

Menerapkan relasi (3), yang berisi turunan Laplace-transformed dari fungsi yang diinginkan dengan kondisi awal, ke persamaan (1), kita dapat memperoleh solusinya sesuai dengan metode yang dikembangkan secara khusus di departemen kami dengan dukungan aktif Scorobey untuk perpustakaan SymPy.

Metode untuk menyelesaikan persamaan diferensial linear dan sistem persamaan berdasarkan transformasi Laplace menggunakan perpustakaan SymPy

Untuk menunjukkan metode ini, kami menggunakan persamaan diferensial sederhana yang menggambarkan gerakan sistem yang terdiri dari titik material dari massa yang diberikan, dipasang pada pegas yang digunakan gaya eksternal. Persamaan diferensial dan kondisi awal untuk sistem tersebut memiliki bentuk:

$x '' + 4x = \ sin (3t); x (0) = 1.2; x '(0) = 1, (4)$

dimana

$x (0)$ - Mengurangi posisi awal massa,

$x '(0)$ - Mengurangi kecepatan massa awal.

Model fisik yang disederhanakan didefinisikan oleh persamaan (4) dengan kondisi awal yang tidak nol [1]:

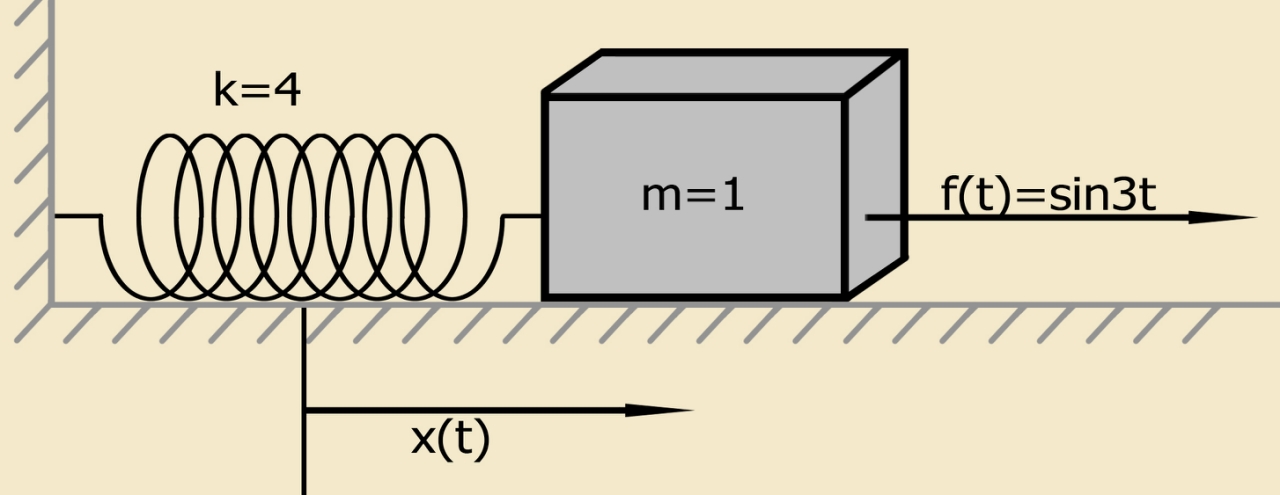
Suatu sistem yang terdiri dari titik material dari massa yang diberikan pada pegas memenuhi masalah Cauchy (masalah dengan kondisi awal). Titik material dari suatu massa pada awalnya diam pada posisi setimbangnya.

Untuk menyelesaikan ini dan persamaan diferensial linear lainnya dengan metode transformasi Laplace, akan lebih mudah untuk menggunakan sistem berikut yang diperoleh dari relasi (3):

L \ kiri \ {f ^ {IV} (t) \ kanan \} = s ^ {4} \ cdot F (s) -s ^ {3} \ cdot f (0) -s ^ {2} \ cdot f ^ {I} (0) -s \ cdot f ^ {II} (0) -f ^ {III} (0),

$L \ kiri \ {f ^ {IV} (t) \ kanan \} = s ^ {4} \ cdot F (s) -s ^ {3} \ cdot f (0) -s ^ {2} \ cdot f ^ {I} (0) -s \ cdot f ^ {II} (0) -f ^ {III} (0),$

L \ kiri \ {f ^ {III} (t) \ kanan \} = s ^ {3} \ cdot f (s) -s ^ {2} \ cdot f (0) -s \ cdot f ^ {I } (0) -f ^ {II} (0),

$L \ kiri \ {f ^ {III} (t) \ kanan \} = s ^ {3} \ cdot f (s) -s ^ {2} \ cdot f (0) -s \ cdot f ^ {I } (0) -f ^ {II} (0),$

L \ kiri \ {f ^ {II} (t) \ kanan \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f ^ {I} (0),

$L \ kiri \ {f ^ {II} (t) \ kanan \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f ^ {I} (0),$

L \ kiri \ {f ^ {I} (t) \ kanan \} = s \ cdot F (s) -f (0), L \ kiri \ {f (t) \ kanan \} = F (s) .

$L \ kiri \ {f ^ {I} (t) \ kanan \} = s \ cdot F (s) -f (0), L \ kiri \ {f (t) \ kanan \} = F (s) .$

L \ kiri \ {f (t) \ kanan \} = F (s). (5)

$L \ kiri \ {f (t) \ kanan \} = F (s). (5)$

Urutan solusi menggunakan SymPy adalah sebagai berikut:

memuat modul yang diperlukan dan secara eksplisit mendefinisikan variabel simbolik:

 from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)

tentukan versi sympy library untuk memperhitungkan fitur-fiturnya. Untuk melakukan ini, masukkan baris berikut:
```
 import SymPy print ('  sympy – %' % (sympy._version_)) 
```
sesuai dengan makna fisik masalah, variabel waktu ditentukan untuk suatu wilayah termasuk nol dan angka positif. Kami menetapkan kondisi awal dan fungsi di sisi kanan persamaan (4) dengan transformasi Laplace berikutnya. Untuk kondisi awal, Anda harus menggunakan fungsi Rasional, karena menggunakan pembulatan desimal menghasilkan kesalahan.
```
 #    : x0 = Rational(6, 5) #   : x01 = Rational(1, 1) g = sin(3*t) Lg = laplace_transform(g, t, s, noconds=True) 
```
menggunakan (5), kami menulis ulang turunan yang dikonversi Laplace yang termasuk dalam sisi kiri persamaan (4), membentuk sisi kiri persamaan ini dari mereka, dan membandingkan hasilnya dengan sisi kanannya:
```
 d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg) 
```
kita memecahkan persamaan aljabar yang diperoleh untuk transformasi X (s) dan melakukan transformasi Laplace terbalik:
```
 rez = solve(de, X(s))[0] soln = inverse_laplace_transform(rez, s, t) 
```
Kami mentransfer dari kantor di perpustakaan SymPy ke perpustakaan NumPy:
```
 f = lambdify(t, soln, 'numpy') 
```

kami memplot metode Python yang biasa:

 x = np.linspace(0, 6*np.pi, 100) plt.title(',     \n  :\n  (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()

Teks lengkap program:

 from sympy import * import numpy as np import matplotlib.pyplot as plt import sympy var('s') var('t', positive=True) var('X', cls=Function) print ("  sympy – %s" % (sympy.__version__)) #       : x0 = Rational(6, 5) #       : x01 = Rational(1, 1) g = sin(3*t) #   : Lg = laplace_transform(g, t, s, noconds=True) d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg) #   : rez = solve(de, X(s))[0] #   : soln = inverse_laplace_transform(rez, s, t) f = lambdify(t, soln, "numpy") x = np.linspace(0, 6*np.pi, 100) plt.title(',     \n  :\n  (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()

Kami mendapatkan:
Versi perpustakaan Sympy - 1.3

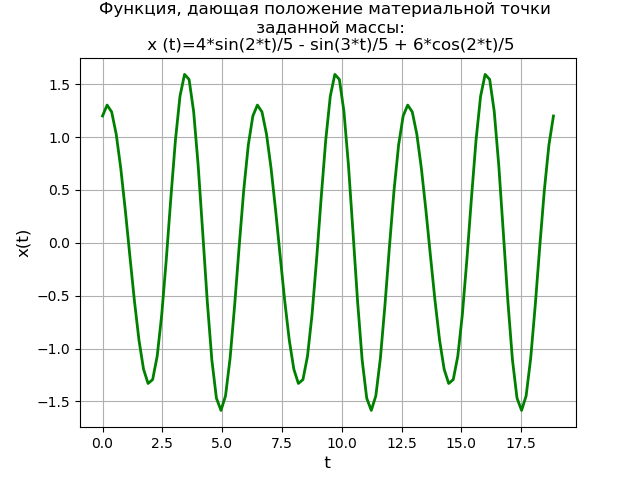
Grafik fungsi periodik yang memberikan posisi titik material dari massa yang diberikan diperoleh. Metode transformasi Laplace menggunakan perpustakaan SymPy memberikan solusi tidak hanya tanpa perlu terlebih dahulu menemukan solusi umum untuk persamaan homogen dan solusi khusus untuk persamaan diferensial heterogen awal, tetapi juga tanpa perlu menggunakan metode fraksi dasar dan tabel Laplace.

Pada saat yang sama, nilai pendidikan dari metode solusi dipertahankan karena kebutuhan untuk menggunakan sistem (5) dan pergi ke NumPy untuk mempelajari solusi menggunakan metode yang lebih produktif.

Untuk mendemonstrasikan metode lebih lanjut, kami memecahkan sistem persamaan diferensial:

$\ begin {cases} 2x '' + 6x-2 = 0, \\ y '' - 2x + 2y = 40 \ cdot \ sin (3t), \ end {cases} (6)$
dengan kondisi awal

$x (0) = y (0) = y '(0) = 0.$

Model fisik yang disederhanakan didefinisikan oleh sistem persamaan (6) di bawah nol kondisi awal:

Dengan demikian, gaya f (t) tiba - tiba diterapkan pada titik material kedua dari massa yang diberikan pada waktu t = 0 , ketika sistem diam pada posisi setimbangnya.

Solusi dari sistem persamaan identik dengan solusi persamaan diferensial yang dipertimbangkan sebelumnya (4), oleh karena itu, saya memberikan teks program tanpa penjelasan.

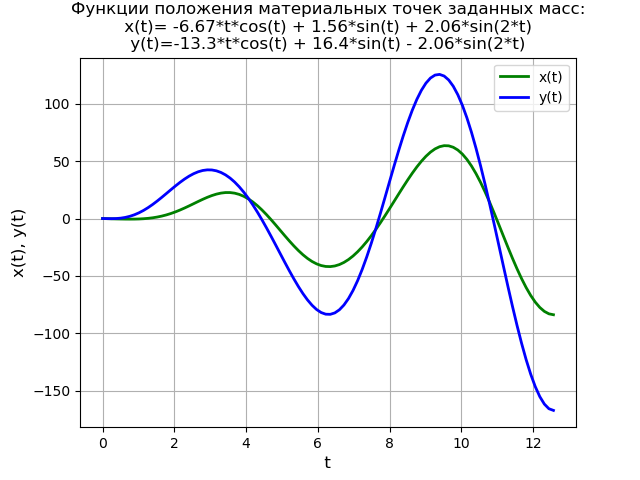
Teks program

 from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t ', positive=True) var('X Y', cls=Function) x0 = 0 x01 = 0 y0 = 0 y01 = 0 g = 40 * sin(3*t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = inverse_laplace_transform(rezX, s, t) rezY = expand(rez[Y(s)]) solnY = inverse_laplace_transform(rezY, s, t) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title('     :\nx(t)=%s\ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()

Kami mendapatkan: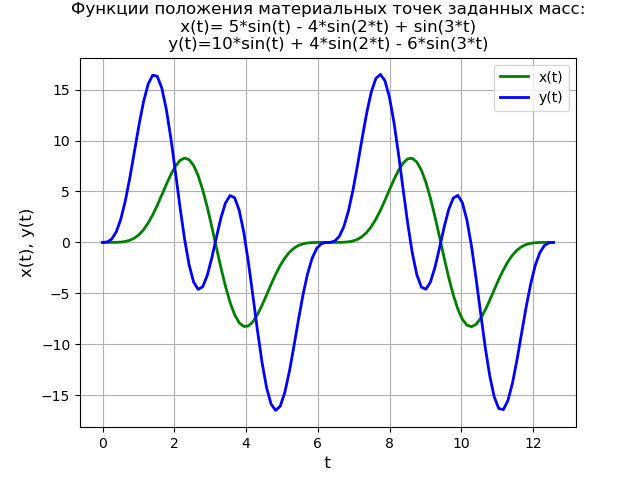

Untuk kondisi awal yang tidak nol, teks program dan grafik fungsi akan berbentuk:

Teks program

 from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X Y', cls=Function) x0 = 0 x01 = -1 y0 = 0 y01 = -1 g = 40 * sin(t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = (inverse_laplace_transform(rezX, s, t)).evalf().n(3) rezY = expand(rez[Y(s)]) solnY = (inverse_laplace_transform(rezY, s, t)).evalf().n(3) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title('     :\nx(t)= %s \ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()

Pertimbangkan solusi persamaan diferensial linear orde keempat dengan nol kondisi awal:

$x ^ {(4)} + 2 \ cdot x '' + x = 4 \ cdot t \ cdot e ^ {t};$

$x (0) = x '(0) = x' '(0) = x ^ {(3)} (0) = 0.$

Teks program:

 from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function) #  : x0 = 0 x01 = 0 x02 = 0 x03 = 0 g = 4*t*exp(t) #   : Lg = laplace_transform(g, t, s, noconds=True) d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03 d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = factor(d4 + 2*d2 + d0) de = Eq(d, Lg) #   : rez = solve(de, X(s))[0] #   : soln = inverse_laplace_transform(rez, s, t) f = lambdify(t, soln, "numpy") x = np.linspace(0, 6*np.pi, 100) plt.title(':\n  (t)=%s\n' % soln, fontsize=11) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()

Jadwal Keputusan:

Kami memecahkan persamaan diferensial linear orde keempat:

$x ^ {(4)} + 13x '' + 36x = 0;$
dengan kondisi awal

$x (0) = x '' (0) = 0$ ,

$x '(0) = 2$ ,

$x ^ {(3)} (0) = - 13$ .

Teks program:

 from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function) #  : x0 = 0 x01 = 2 x02 = 0 x03 = -13 d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03 d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = factor(d4 + 13*d2 + 36*d0) de = Eq(d, 0) #   : rez = solve(de, X(s))[0] #   : soln = inverse_laplace_transform(rez, s, t) f = lambdify(t, soln, "numpy") x = np.linspace(0, 6*np.pi, 100) plt.title(':\n  (t)=%s\n' % soln, fontsize=11) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()

Jadwal Keputusan: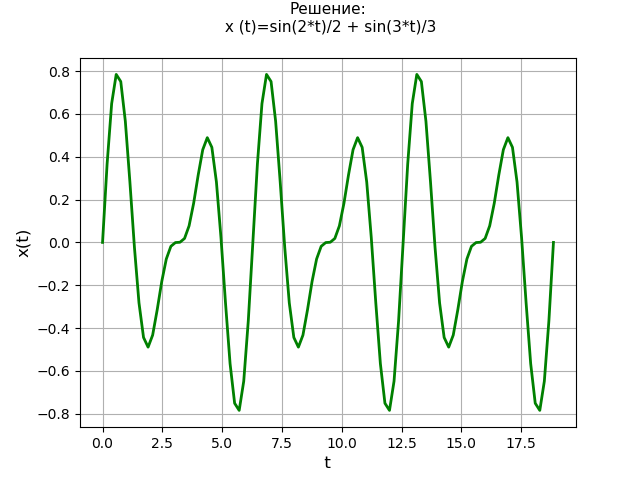

Fungsi untuk memecahkan ODE

Untuk sistem ODE dan ODE dengan solusi analitis, fungsi dsolve () digunakan:
sympy.solvers.ode. dsolve (eq, func = None, hint = 'default', simplify = True, ics = None, xi = None, eta = None, x0 = 0, n = 6, ** kwargs)

Mari kita bandingkan kinerja fungsi dsolve () dengan metode Laplace. Misalnya, ambil persamaan diferensial derajat keempat berikut dengan nol kondisi awal:

$x ^ {(IV)} (t) = 3 \ cdot x '' '(t) -x (t) = 4 \ cdot t \ cdot \ exp (t);$

$x (0) = x '(0) = x' '(0) = x' '' (0) = 0.$

Program yang menggunakan fungsi dsolve ():

 from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('t C1 C2 C3 C4') u = Function("u")(t) #   : de = Eq(u.diff(t, t, t, t) - 3*u.diff(t, t, t) + 3*u.diff(t, t) - u.diff(t), 4*t*exp(t)) #   : des = dsolve(de, u) #  : eq1 = des.rhs.subs(t, 0) eq2 = des.rhs.diff(t).subs(t, 0) eq3 = des.rhs.diff(t, t).subs(t, 0) eq4 = des.rhs.diff(t, t, t).subs(t, 0) #       : seq = solve([eq1, eq2-1, eq3-2, eq4-3], C1, C2, C3, C4) rez = des.rhs.subs([(C1, seq[C1]), (C2, seq[C2]), (C3, seq[C3]), (C4, seq[C4])]) def F(t): return rez f = lambdify(t, rez, 'numpy') x = np.linspace(0, 6*np.pi, 100) stop = time.time() print ('      dsolve(): %ss' % round((stop-start), 3)) plt.title('    dsolve():\n  (t)=%s\n' % rez, fontsize=11) plt.grid(True) plt.xlabel('Time t seconds', fontsize=12) plt.ylabel('f(t)', fontsize=16) plt.plot(x, f(x), color='#008000', linewidth=3) plt.show()

Kami mendapatkan:

Waktu persamaan menggunakan fungsi dsolve (): 1.437 dtk

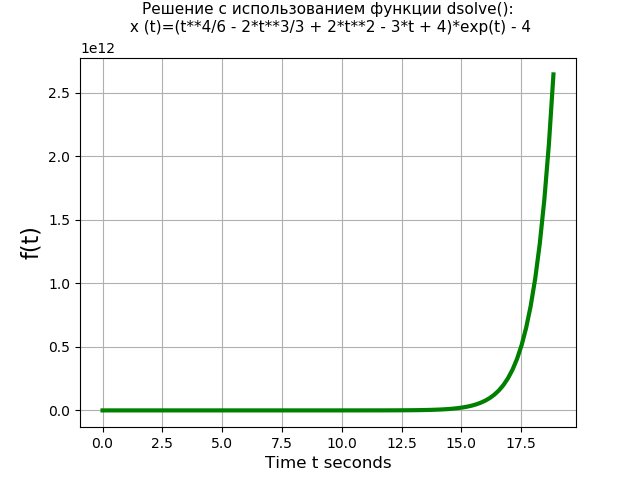
Program menggunakan transformasi Laplace:

 from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('s') var('t', positive=True) var('X', cls=Function) #  : x0 = 0 x01 = 0 x02 = 0 x03 = 0 #     : g = 4*t*exp(t) #   : Lg = laplace_transform(g, t, s, noconds=True) d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03 d3 = s**3*X(s) - s**2*x0 - s*x01 - x02 d2 = s**2*X(s) - s*x0 - x01 d1 = s*X(s) - x0 d0 = X(s) #     : d = factor(d4 - 3*d3 + 3*d2 - d1) de = Eq(d, Lg) #   : rez = solve(de, X(s))[0] #   : soln = collect(inverse_laplace_transform(rez, s, t), t) f = lambdify(t, soln, 'numpy') x = np.linspace(0, 6*np.pi, 100) stop = time.time() print ('      : %ss' % round((stop-start), 3)) plt.title('    :\n  (t)=%s\n' % soln, fontsize=11) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()

Kami mendapatkan:

Waktu persamaan menggunakan Transformasi Laplace: 3.274 dtk

Jadi, fungsi dsolve () (1,437 dtk) memecahkan persamaan urutan keempat lebih cepat daripada memecahkan dengan metode transformasi Laplace (3,274 dtk) lebih dari dua kali. Namun, perlu dicatat bahwa fungsi dsolve () tidak menyelesaikan sistem persamaan diferensial orde kedua, misalnya, ketika menyelesaikan sistem (6) menggunakan fungsi dsolve (), kesalahan terjadi:

 from sympy import* t = symbols('t') x, y = symbols('x, y', Function=True) eq = (Eq(Derivative(x(t), t, 2), -3*x(t) + y(t)), Eq(Derivative(y(t), t, 2), 2*x(t) - 2*y(t) + 40*sin(3*t))) rez = dsolve(eq) print (list(rez))

Kami mendapatkan:

meningkatkanNotImplementedError
NotImplementedError

Kesalahan ini berarti bahwa solusi dari sistem persamaan diferensial menggunakan fungsi dsolve () tidak dapat direpresentasikan secara simbolis. Sedangkan dengan bantuan transformasi Laplace kami mendapat representasi simbolis dari solusi, dan ini membuktikan efektivitas metode yang diusulkan.

Catatan

Untuk menemukan metode yang diperlukan untuk menyelesaikan persamaan diferensial menggunakan fungsi dsolve () , Anda perlu menggunakan classify_ode (eq, f (x)) , misalnya:

 from sympy import * from IPython.display import * import matplotlib.pyplot as plt init_printing(use_latex=True) x = Symbol('x') f = Function('f') eq = Eq(f(x).diff(x, x) + f(x), 0) print (dsolve(eq, f(x))) print (classify_ode(eq, f(x))) eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) print (classify_ode(eq, f(x))) rez = dsolve(eq, hint='almost_linear_Integral') print (rez)

Kami mendapatkan:

Persamaan (f (x), C1 * sin (x) + C2 * cos (x))
('nth_linear_constant_coeff_homogeneous', '2nd_power_series_ordinary')
('dapat dipisahkan', '1st_exact', 'hampir_linear', '1st_power_series', 'lie_group', 'separable_Integral', '1st_exact_Integral', 'almost_linear_Integral')
[Eq (f (x), -acos ((C1 + Integral (0, x)) * exp (-Integral (-tan (x), x))) + 2 * pi), Eq (f (x), acos ((C1 + Integral (0, x)) * exp (-Integral (-tan (x), x)))]]]

Jadi, untuk persamaan eq = Eq (f (x) .diff (x, x) + f (x), 0) , semua metode dari daftar pertama berfungsi:

nth_linear_constant_coeff_homogeneous,
2nd_power_series_ Biasa

Untuk persamaan eq = sin (x) * cos (f (x)) + cos (x) * sin (f (x)) * f (x) .diff (x) , semua metode dari daftar kedua berfungsi:

dipisahkan, 1st_exact, hampir_linear,
1st_power_series, lie_group, separable_Integral,
1st_exact_Integral, almost_linear_Integral

Untuk menggunakan metode yang dipilih, entri fungsi dsolve () akan berbentuk, misalnya:

 rez = dsolve(eq, hint='almost_linear_Integral')

Kesimpulan:

Artikel ini bertujuan untuk menunjukkan bagaimana menggunakan alat perpustakaan SciPy dan NumPy pada contoh pemecahan sistem ODE linier menggunakan metode operator. Dengan demikian, metode solusi simbolik dari persamaan diferensial linear dan sistem persamaan dengan metode Laplace dipertimbangkan. Analisis kinerja metode ini dan metode yang diterapkan dalam fungsi dsolve () dilakukan.

Referensi:

Persamaan diferensial dan masalah nilai batas: pemodelan dan perhitungan menggunakan Mathematica, Maple dan MATLAB. Edisi ke-3: Per. dari bahasa inggris - M.: LLC “Saya. Williams, 2008. - 1104 p .: Ill. - Paral. dada. Bahasa inggris
Menggunakan transformasi Laplace terbalik untuk menganalisis tautan dinamis sistem kontrol

Solusi simbolik dari persamaan diferensial linear dan sistem dengan metode transformasi Laplace menggunakan SymPy

Kisah kepenulisan Laplace berubah

Fungsi transformasi Laplace langsung dan terbalik

Transformasi Laplace terbalik pada contoh menentukan karakteristik transisi dari regulator

Transformasi Laplace dari turunan dari pesanan yang lebih tinggi untuk menyelesaikan masalah Cauchy

Metode untuk menyelesaikan persamaan diferensial linear dan sistem persamaan berdasarkan transformasi Laplace menggunakan perpustakaan SymPy

Fungsi untuk memecahkan ODE

Kesimpulan:

More articles: