Pelajari OpenGL. Pelajaran 6.1. PBR atau Rendering yang Tepat Secara Fisik. Teori

Rendering yang Tepat Secara Fisik

PBR, atau rendering berbasis fisik, adalah seperangkat teknik visualisasi yang didasarkan pada teori yang setuju dengan teori propagasi cahaya yang sebenarnya. Karena tujuan PBR adalah simulasi cahaya yang andal secara fisik, ia tampak jauh lebih realistis dibandingkan dengan model pencahayaan Phong dan Blinn-Fong yang kami gunakan sebelumnya. Itu tidak hanya terlihat lebih baik, tetapi juga memberikan perkiraan yang baik untuk fisika nyata, yang memungkinkan kita (dan seniman khususnya) untuk membuat bahan berdasarkan sifat fisik permukaan tanpa menggunakan trik murah untuk membuat pencahayaan terlihat realistis. Keuntungan utama dari pendekatan ini adalah bahwa bahan yang kami buat akan terlihat seperti yang direncanakan terlepas dari kondisi pencahayaan, yang tidak dapat dikatakan tentang pendekatan lain, bukan PBR.

Namun, PBR masih merupakan perkiraan realitas (berdasarkan hukum fisika), oleh karena itu disebut rendering yang benar secara fisik daripada rendering fisik. Agar model pencahayaan dapat disebut benar secara fisik, harus memenuhi 3 kondisi (jangan khawatir, kita akan segera mendapatkannya):

• Berdasarkan model segi mikro reflektif
• Patuhi hukum kekekalan energi
• Gunakan fungsi distribusi reflektansi berkas-ganda (BRDF)

Dalam seri tutorial ini, kami akan fokus pada pendekatan PBR, yang awalnya dikembangkan di Disney dan diadaptasi untuk visualisasi waktu nyata oleh Epic Games. Pendekatan mereka, berdasarkan alur kerja logam-dielektrik ( Alur kerja logam, tidak dapat menemukan terjemahan yang lebih baik - kira-kira. Ed. ), Didokumentasikan dengan baik, diterima secara luas di banyak mesin populer dan terlihat luar biasa. Di akhir bagian ini, kami mendapatkan sesuatu yang mirip dengan ini:

Ingatlah bahwa artikel di bagian ini cukup canggih, sehingga Anda disarankan untuk memiliki pemahaman yang baik tentang OpenGL dan pencahayaan shader. Berikut adalah beberapa pengetahuan yang Anda perlukan untuk mempelajari bagian ini: frame buffer , peta kubik , koreksi gamma , HDR, dan peta normal . Kita juga akan masuk sedikit ke dalam matematika, tetapi saya berjanji untuk melakukan segala yang mungkin untuk menjelaskan semuanya sejelas mungkin.

Model segi mikro reflektif

Semua teknik PBR didasarkan pada teori wajah mikro. Teori ini mengatakan bahwa setiap permukaan dengan perbesaran tinggi dapat direpresentasikan sebagai satu set cermin mikroskopis yang disebut muka mikro . Karena kekasaran permukaan, cermin mikro ini dapat diorientasikan ke arah yang berbeda:

Semakin kasar permukaannya, semakin acak wajah mikronya. Hasil dari pengaturan cermin-cermin kecil ini adalah (khususnya ketika menyangkut flare dan pantulan specular) bahwa sinar datang tersebar di berbagai arah pada permukaan kasar, yang mengarah pada flare specular yang lebih luas. Dan sebaliknya: pada permukaan yang halus, sinar datang lebih cenderung tercermin dalam satu arah, yang akan memberikan silau yang lebih kecil dan lebih tajam:

Pada tingkat mikroskopis, tidak ada permukaan yang benar-benar halus, tetapi mengingat bahwa permukaan mikro cukup kecil dan kami tidak dapat membedakannya dalam ruang piksel kami, kami secara statistik memperkirakan kekasaran permukaan dengan memperkenalkan koefisien kekasaran . Dengan menggunakan koefisien ini, kita dapat menghitung fraksi wajah mikro yang berorientasi ke arah vektor tertentu $$$h$ . Vektor ini $$$h$ tidak lebih dari vektor median yang terletak di tengah-tengah antara arah cahaya yang datang $$$l$ dan arah pengamat $$$v$ . Kami membicarakannya sebelumnya dalam pelajaran tentang pencahayaan tingkat lanjut , di mana kami mendefinisikannya sebagai rasio jumlah vektor $$$l$ dan $$$v$ dengan panjang vektor yang dihasilkan:

$$

$$h = \ frac {l + v} {|| l + v ||}$$

Semakin banyak wajah mikro yang berorientasi ke arah vektor median, sorot specular akan semakin tajam dan cerah. Karena koefisien kekasaran, yang terletak antara 0 dan 1, kami dapat memperkirakan secara statistik orientasi wajah mikro:

Seperti yang Anda lihat, nilai yang lebih tinggi dari koefisien kekasaran memberikan titik flare cermin dengan ukuran yang lebih besar, dibandingkan dengan titik kecil dan tajam pada permukaan halus.

Konservasi energi.

Menggunakan perkiraan dengan memperhitungkan permukaan mikro sudah membawa bentuk tertentu dari konservasi energi: energi cahaya yang dipantulkan tidak akan pernah melebihi energi cahaya yang datang (jika permukaan tidak bersinar dengan sendirinya). Melihat gambar di atas, kita melihat bahwa dengan peningkatan kekasaran permukaan, titik cahaya yang dipantulkan meningkat, tetapi pada saat yang sama kecerahannya menurun. Jika intensitas cahaya yang dipantulkan sama untuk semua piksel, terlepas dari ukuran tempat, maka permukaan yang lebih kasar akan memancarkan lebih banyak energi, yang akan melanggar hukum kekekalan energi. Oleh karena itu, pantulan specular lebih cerah pada permukaan yang halus dan redup pada permukaan yang kasar.

Agar energi dapat dilestarikan, kita harus membuat pemisahan yang jelas antara komponen difus dan cermin. Pada saat itu, ketika sinar cahaya mencapai permukaan, ia dibagi menjadi komponen yang dipantulkan dan dibiaskan . Komponen yang dipantulkan adalah cahaya yang dipantulkan langsung dan tidak menembus permukaan, kita tahu itu sebagai komponen cermin cahaya. Komponen yang dibiaskan adalah cahaya yang menembus permukaan dan diserap olehnya - diketahui oleh kita sebagai komponen cahaya yang menyebar.

Tetapi ada beberapa nuansa yang terkait dengan penyerapan cahaya - itu tidak terjadi secara instan, begitu cahaya menyentuh permukaan. Dari arah fisika, kita tahu bahwa cahaya dapat digambarkan sebagai seberkas foton dengan energi yang bergerak dalam garis lurus hingga kehilangan semua energi sebagai akibat tabrakan dengan rintangan. Setiap bahan terdiri dari partikel mikro yang dapat berinteraksi dengan sinar cahaya, seperti yang ditunjukkan pada gambar di bawah ini. Partikel-partikel ini menyerap sebagian atau seluruh energi cahaya di setiap tabrakan, mengubahnya menjadi panas.

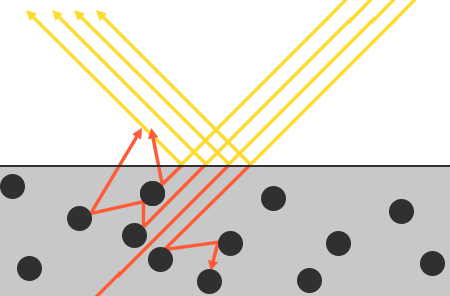
Dalam kasus umum, tidak semua energi diserap, dan cahaya terus menyebar ke arah (terutama) acak, di mana ia kembali bertabrakan dengan partikel lain sampai kehabisan energi atau meninggalkan permukaan lagi. Dengan demikian, permukaan mulai memancarkan kembali sinar cahaya, membuat kontribusi dalam bentuk warna permukaan yang diamati (difus). Menggunakan PBR, kami membuat asumsi yang disederhanakan bahwa semua cahaya yang dibiaskan diserap dan tersebar di area pengaruh yang kecil, mengabaikan efek cahaya yang tersebar yang meninggalkan permukaan pada jarak dari area ini. Teknik shader khusus yang memperhitungkan hal ini, dikenal sebagai teknik hamburan di bawah permukaan , sangat meningkatkan kualitas visual dari bahan-bahan seperti kulit, marmer, lilin, tetapi mahal dalam hal kinerja.

Kehalusan tambahan muncul ketika cahaya dibiaskan dan dipantulkan pada permukaan logam . Permukaan logam berinteraksi secara berbeda dengan cahaya dibandingkan non-logam (mis., Dielektrik). Mereka mematuhi hukum pembiasan dan refleksi yang sama, dengan satu pengecualian: semua cahaya yang dibiaskan diserap oleh permukaan tanpa hamburan, hanya cahaya yang dipantulkan cermin yang tersisa; dengan kata lain, permukaan logam tidak memiliki warna difus. Karena perbedaan yang jelas antara logam dan dielektrik ini, mereka akan diproses secara berbeda dalam konveyor PBR di mana kita akan melangkah lebih jauh dalam perjalanan artikel ini.

Perbedaan antara cahaya yang dipantulkan dan dibiaskan ini membawa kita ke pengamatan lain mengenai konservasi energi: nilainya saling eksklusif. Energi cahaya yang dipantulkan tidak dapat diserap oleh material. Oleh karena itu, energi yang diserap oleh permukaan dalam bentuk cahaya yang dibiaskan adalah energi yang tersisa setelah memperhitungkan cahaya yang dipantulkan.
Kami menggunakan rasio ini, menghitung pertama bagian yang dipantulkan sebagai persentase energi dari sinar yang dipantulkan oleh permukaan, dan kemudian fraksi cahaya yang dibiaskan langsung dari pantulan, sebagai:

float kS = calculateSpecularComponent(...); // /  float kD = 1.0 - kS; // /  

Dengan cara ini kita mempelajari makna dari bagian yang dipantulkan dan dibiaskan berkat hukum kekekalan energi. Dengan pendekatan ini, baik bagian yang dibiaskan (difus) maupun yang dipantulkan tidak akan melebihi 1,0, memastikan bahwa total energi mereka tidak melebihi nilai energi cahaya yang terjadi, yang tidak dapat kami perhitungkan dalam pelajaran sebelumnya.

Persamaan refleksi

Di atas membawa kita ke apa yang disebut persamaan rendering : persamaan kompleks yang diciptakan oleh orang-orang yang sangat pintar, dan hari ini adalah model terbaik untuk mensimulasikan pencahayaan. PBR secara ketat mengikuti versi yang lebih spesifik dari persamaan ini, yang dikenal sebagai persamaan refleksi . Untuk memahami PBR dengan baik, penting untuk terlebih dahulu memiliki pemahaman yang lengkap tentang persamaan refleksi:

$$

$$L_o (p, \ omega_o) = \ int \ limit_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

Pada awalnya itu terlihat menakutkan, tetapi kami akan membukanya secara bertahap, dalam beberapa bagian, dan Anda akan melihat betapa lambatnya itu akan mulai masuk akal. Untuk memahami persamaan ini kita harus sedikit lebih dalam ke radiometri. Radiometri adalah ilmu untuk mengukur radiasi elektromagnetik (termasuk cahaya tampak). Ada beberapa jumlah radiometrik yang dapat kita gunakan untuk mengukur iluminasi, tetapi kita hanya akan menggunakan satu yang berhubungan dengan persamaan refleksi, yang dikenal sebagai Energy Luminance (bahasa Inggris bercahaya) dan ditunjuk di sini oleh huruf L. EI digunakan untuk mengukur besarnya atau intensitas cahaya, datang dari arah tertentu. EJ, pada gilirannya, adalah kombinasi dari beberapa kuantitas fisik, dan agar lebih mudah bagi kita untuk membayangkannya, kita akan fokus pada masing-masing secara individual.

Radiasi Fluks

Fluks radiasi ( $$$\ Phi$ ) adalah kekuatan energi cahaya yang ditransmisikan, diukur dalam watt. Energi total cahaya terdiri dari banyak istilah untuk panjang gelombang yang berbeda, yang masing-masing sesuai dengan warna spektrumnya sendiri. Energi yang dipancarkan oleh sumber cahaya, dalam hal ini, dapat direpresentasikan sebagai fungsi dari semua panjang gelombang ini. Panjang gelombang dari 390nm hingga 700nm membentuk bagian spektrum yang terlihat, yaitu radiasi dalam kisaran ini dapat dirasakan oleh mata manusia. Pada gambar di bawah ini Anda dapat melihat nilai-nilai energi untuk panjang gelombang berbeda yang membentuk siang hari:

Fluks radiasi sesuai dengan area di bawah grafik fungsi ini untuk semua panjang gelombang. Penggunaan langsung dari panjang gelombang cahaya sebagai input dalam grafik komputer tidak praktis, jadi kami menggunakan representasi sederhana dari fluks radiasi, alih-alih menggunakan fungsi dari semua panjang gelombang, triplet warna, dikenal sebagai RGB (atau, seperti biasa kita sebut, warna pencahayaan). Pandangan seperti itu menyebabkan hilangnya informasi, tetapi secara keseluruhan itu akan sedikit mempengaruhi gambaran akhir.

Sudut yang solid

Sudut padat dilambangkan dengan $$$\ omega$ memberi kita ukuran atau luas gambar yang diproyeksikan ke unit sphere. Anda dapat membayangkannya sebagai arah yang memiliki volume:

Bayangkan Anda berada di tengah bola dan melihat ke arah gambar itu. Ukuran siluet yang dihasilkan akan menjadi sudut yang solid.

Intensitas radiasi

Kekuatan radiasi mengukur jumlah fluks radiasi per sudut padat, atau kekuatan sumber cahaya per satuan luas yang ditentukan oleh sudut padat. Misalnya, untuk sumber cahaya omnidirectional yang sama-sama memancarkan ke segala arah, gaya radiasi berarti energi cahaya per area tertentu (sudut padat):

Persamaan yang menggambarkan kekuatan radiasi terlihat seperti ini:

$$

$$I = \ frac {d \ Phi} {d \ omega}$$

, di mana I adalah fluks radiasi per sudut padat $$${d \ omega}$

Mengetahui fluks radiasi, gaya, dan sudut solid, kita dapat menggambarkan persamaan kecerahan energi yang menggambarkan total energi yang diamati di area A, dibatasi oleh sudut padat O untuk cahaya dengan gaya. $$$\ Phi$

$$

$$L = \ frac {d ^ 2 \ Phi} {dA d \ omega \ cos \ theta}$$

Kecerahan energi adalah kuantitas radiometrik cahaya di area yang bergantung pada sudut cahaya yang datang. $$$\ theta$ (sudut antara arah cahaya dan normal ke permukaan) melalui $$$cos \ theta$ : Cahaya lebih lemah ketika dipancarkan di sepanjang permukaan dan lebih kuat ketika tegak lurus terhadapnya. Ini mirip dengan perhitungan kami untuk cahaya difus dalam tutorial tentang dasar-dasar pencahayaan sejak itu $$$cos \ theta$ tidak lebih dari produk skalar antara arah cahaya dan vektor normal ke permukaan:

 float cosTheta = dot(lightDir, N); 

Persamaan kecerahan energi sangat berguna bagi kita, karena mengandung sebagian besar jumlah fisik yang menarik bagi kita. Jika kita mengasumsikan bahwa sudut padat ω dan area A sangat kecil, kita dapat menggunakan EE untuk mengukur fluks satu sinar cahaya per satu titik dalam ruang. Ini akan memungkinkan kita untuk menghitung EI dari sinar tunggal yang bekerja pada satu titik (fragmen); kami benar-benar menerjemahkan sudut yang solid $$$\ omega$ dalam vektor arah $$$\ omega$ dan $$$A$ to the point $$$p$ . Dengan demikian, kita dapat langsung menggunakan EI di shader kami untuk menghitung kontribusi sinar cahaya tunggal untuk setiap fragmen.

Bahkan, ketika datang ke EE, kita biasanya tertarik pada semua insiden cahaya yang masuk pada titik p, yang merupakan jumlah dari seluruh EE, dan dikenal sebagai irradiansi. Mengetahui EI dan iradiasi, kita dapat kembali ke persamaan refleksi:

$$

$$L_o (p, \ omega_o) = \ int \ limit_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

Sekarang kita tahu itu $$$L$ dalam persamaan render adalah EI untuk beberapa titik pada permukaan p dan beberapa sudut padat kecil dari cahaya yang masuk $$$\ omega_i$ , yang dapat dianggap sebagai vektor arah input $$$\ omega_i$ . Ingatlah bahwa energi dikalikan dengan $$$cos \ theta$ - sudut antara arah timbulnya cahaya dan normal ke permukaan, yang dinyatakan dalam persamaan refleksi oleh produk $$$n \ cdot \ omega_i$ . Persamaan refleksi menghitung jumlah EI yang direfleksikan $$$L_o (p, \ omega_o)$ poin $$$p$ menuju $$$ω_o$ , yang merupakan arah keluar ke pengamat. Atau yang lain: $$$L_o$ mengukur irradiansi pantulan suatu titik $$$p$ jika dilihat dari $$$\ omega_o$ .

Karena persamaan refleksi didasarkan pada iradiasi, yang merupakan jumlah dari semua radiasi yang masuk, kami mengukur cahaya tidak hanya dari satu arah cahaya yang masuk, tetapi dari semua arah cahaya yang masuk dalam belahan bumi. $$$\ Omega$ berpusat di $$$p$ . Ini dapat digambarkan sebagai setengah bola yang berorientasi sepanjang permukaan normal $$$n$ :

Untuk menghitung jumlah semua nilai di dalam wilayah, atau, dalam kasus belahan bumi, volume, kami mengintegrasikan persamaan di semua arah yang masuk $$$d \ omega_i$ dalam belahan bumi $$$\ Omega$ . Karena tidak ada solusi analitik untuk persamaan render dan persamaan refleksi, kami akan menyelesaikan integralnya secara numerik. Ini berarti bahwa kita akan memperoleh hasil untuk langkah-langkah diskrit kecil dari persamaan refleksi belahan bumi $$$\ Omega$ dan rata-rata di atas ukuran langkah. Ini disebut jumlah Riemann , yang secara kasar dapat kita wakili dengan kode berikut:

 int steps = 100; float sum = 0.0f; vec3 P = ...; vec3 Wo = ...; vec3 N = ...; float dW = 1.0f / steps; for(int i = 0; i < steps; ++i) { vec3 Wi = getNextIncomingLightDir(i); sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW; } 

dW untuk setiap langkah diskrit dapat dianggap sebagai $$$d \ omega_i$ dalam persamaan refleksi. Secara matematis $$$d \ omega_i$ adalah diferensial dengan mana kita menghitung integral, dan meskipun tidak sama dengan dW dalam kode (karena ini adalah langkah terpisah dari jumlah Riemann), kita dapat mempertimbangkannya untuk kemudahan perhitungan. Perlu diingat bahwa menggunakan langkah-langkah terpisah akan selalu memberi kami jumlah perkiraan, bukan nilai yang tepat dari integral. Pembaca yang penuh perhatian akan memperhatikan bahwa kita dapat meningkatkan akurasi jumlah Riemann dengan meningkatkan jumlah langkah.

Persamaan refleksi menjumlahkan radiasi dari semua arah cahaya yang masuk $$$\ omega_i$ belahan bumi $$$\ Omega$ yang mencapai titik $$$p$ dan mengembalikan jumlah cahaya yang dipantulkan $$$L_o$ menuju pemirsa. Radiasi yang masuk dapat berasal dari sumber cahaya yang sudah kita kenal, atau dari peta lingkungan yang menentukan EI dari setiap arah yang masuk, yang akan kita bicarakan dalam tutorial IBL.

Sekarang satu-satunya yang tidak diketahui di sebelah kiri adalah simbol $$$f_r$ , yang dikenal sebagai fungsi BRDF atau fungsi reflektansi dua-balok , yang mengukur (atau menimbang) nilai radiasi yang masuk berdasarkan sifat-sifat material permukaan.

BRDF

BRDF adalah fungsi yang menerima arah cahaya insiden. $$$\ omega_i$ , arah ke pengamat $$$\ omega_o$ normal ke permukaan $$$n$ dan parameter $$$a$ , Yang merupakan kekasaran permukaan. BRDF memperkirakan seberapa besar masing-masing berkas cahaya individu $$$\ omega_i$ berkontribusi terhadap cahaya pantulan terakhir dari permukaan buram, dengan mempertimbangkan sifat materialnya. Misalnya, jika permukaan benar-benar halus (hampir seperti cermin), fungsi BRDF akan mengembalikan 0,0 untuk semua sinar cahaya yang masuk $$$\ omega_i$ kecuali satu memiliki sudut yang sama (setelah refleksi) sebagai balok $$$\ omega_o$ yang fungsinya akan mengembalikan 1.0.

BRDF mendekati sifat reflektif dan bias dari bahan berdasarkan teori yang disebutkan sebelumnya tentang permukaan mikro. Agar BRDF masuk akal secara fisik, ia harus mematuhi hukum kekekalan energi, yaitu, total energi dari cahaya yang dipantulkan tidak boleh melebihi energi dari cahaya yang terjadi. Secara teknis, model Blinn-Fong dianggap sebagai BRDF yang menerima hal yang sama $$$\ omega_i$ dan $$$\ omega_o$ di pintu masuk. Namun, model Blinn-Fong tidak dianggap benar secara fisik, karena tidak menjamin kepatuhan terhadap hukum konservasi energi. Ada beberapa BRDF yang benar secara fisik untuk memperkirakan respons permukaan terhadap pencahayaan. Namun, hampir semua pipa grafis real-time menggunakan BRDF, yang dikenal sebagai Cook-Torrance BRDF .

Cook-Torrens BRDF mengandung bagian difus dan cermin:

$$

$$f_r = k_df_ {lambert} + k_sf_ {cook - torrance}$$

disini $$$k_d$ - Fraksi refraksi dari energi cahaya yang masuk, $$$k_s$ - tercermin. Sisi kiri BRDF berisi bagian difus dari persamaan, dilambangkan di sini sebagai $$$f_ {lambert}$ . Inilah yang disebut hamburan Lambert. Ini mirip dengan apa yang kami gunakan untuk pencahayaan difus, dan konstan:

$$

$$f_ {lambert} = \ frac {c} {\ pi}$$

dimana $$$c$ - Albedo atau warna permukaan (tekstur permukaan difus). Divisi oleh $$$\ pi$ diperlukan untuk menormalkan cahaya yang tersebar, karena integral yang sebelumnya ditunjukkan mengandung BRDF dikalikan dengan $$$\ pi$ (kita akan membahas ini dalam tutorial IBL).

Anda mungkin terkejut melihat bagaimana hamburan Lambertian ini menyerupai ekspresi untuk pencahayaan difus yang kami gunakan sebelumnya: warna permukaan dikalikan dengan produk skalar antara permukaan normal dan arah cahaya. Produk skalar masih ada, tetapi disimpulkan dari BRDF, karena sudah ada $$$n \ cdot \ omega_i$ dalam integral $$$L_o$ .

Ada berbagai persamaan untuk bagian difus BRDF yang terlihat lebih realistis, tetapi mereka lebih mahal dalam hal kinerja. Selain itu, seperti yang disimpulkan Epic Games: Hamburan Lambertian cukup untuk sebagian besar keperluan rendering waktu-nyata.

Bagian cermin dari Cook-Torrens BRDF sedikit ditingkatkan dan digambarkan sebagai:

$$

$$f_ {cook - torrance} = \ frac {DFG} {4 (\ omega_o \ cdot n) (\ omega_i \ cdot n)}$$

Ini terdiri dari tiga fungsi dan koefisien standardisasi dalam penyebut. Setiap huruf D, F, dan G mewakili tipe fungsi tertentu yang mendekati bagian tertentu dari sifat reflektif permukaan. Mereka dikenal sebagai fungsi distribusi normal (NDF), persamaan Fresnel, dan fungsi Geometri:

• Fungsi distribusi normal: mendekati jumlah permukaan mikro yang berorientasi sepanjang vektor median, berdasarkan kekasaran permukaan; Ini adalah fungsi utama yang mendekati permukaan mikro.
• Fungsi geometri: menggambarkan properti bayangan wajah mikro. Ketika permukaan agak kasar, beberapa permukaan mikro dari permukaan dapat tumpang tindih dengan yang lain, sehingga mengurangi jumlah cahaya yang dipantulkan oleh permukaan.
• Persamaan Fresnel: menggambarkan koefisien pantulan permukaan pada sudut yang berbeda.

Masing-masing fungsi ini merupakan perkiraan ekuivalen fisiknya, dan bagi mereka ada berbagai implementasi yang ditujukan pada perkiraan yang lebih akurat terhadap model fisik yang mendasarinya; beberapa memberikan hasil yang lebih realistis, yang lain lebih efektif dalam hal kinerja. Brian Caris dari Epic Games telah melakukan banyak penelitian tentang berbagai jenis pendekatan, yang dapat Anda pelajari lebih lanjut di sini . Kami akan menggunakan fungsi yang sama seperti di Unreal Engine 4 dari Epic Games, yaitu: Trowbridge-Reitz GGX untuk D, perkiraan Fresnel-Schlick untuk F dan Smith's Schlick-GGX untuk G.

Fungsi distribusi normal

Fungsi distribusi normal D secara statistik mendekati luas permukaan relatif dari permukaan mikro yang secara tepat berorientasi sepanjang vektor median $$$h$ . Ada banyak NDF yang menentukan perkiraan statistik dari keselarasan muka mikro secara keseluruhan dengan mempertimbangkan beberapa parameter kekasaran. Kami akan menggunakan yang dikenal sebagai Trowbridge-Reitz GGX:

$$

$$NDF_ {GGXTR} (n, h, \ alpha) = \ frac {\ alpha ^ 2} {\ pi ((n \ cdot h) ^ 2 (\ alpha ^ 2−1) +1) ^ 2}$$

disini $$$h$ Apakah vektor median, $$$\ alpha$ - nilai kekasaran permukaan. Jika kita memilih $$$h$ sebagai vektor median antara normal ke permukaan dan arah cahaya, kemudian mengubah parameter kekasaran, kita mendapatkan gambar berikut:

Ketika kekasaran kecil (mis., Permukaan halus), permukaan mikro yang berorientasi ke arah vektor median terkonsentrasi dalam radius kecil. Karena konsentrasi tinggi ini, NDF memberikan titik yang sangat cerah. Pada permukaan kasar, di mana wajah mikro berorientasi ke arah yang lebih acak, Anda akan menemukan lebih banyak wajah mikro yang berorientasi pada arah vektor median $$$h$ tetapi terletak di radius yang lebih besar, yang membuat warna spot lebih abu-abu.

Dalam kode GLSL, fungsi distribusi normal Trowbridge-Reitz GGX akan terlihat seperti ini:

 float DistributionGGX(vec3 N, vec3 H, float a) { float a2 = a*a; float NdotH = max(dot(N, H), 0.0); float NdotH2 = NdotH*NdotH; float nom = a2; float denom = (NdotH2 * (a2 - 1.0) + 1.0); denom = PI * denom * denom; return nom / denom; } 

Fungsi geometri

Fungsi geometri secara statistik mendekati luas permukaan relatif, di mana penyimpangan mikroskopisnya tumpang tindih, yang mencegah sinar cahaya menembus.

Seperti dalam kasus NDF, fungsi geometri menerima koefisien kekasaran permukaan sebagai input, yang dalam hal ini berarti sebagai berikut: permukaan yang lebih kasar akan memiliki kemungkinan lebih tinggi untuk naungan muka mikro. Fungsi geometri yang akan kita gunakan adalah kombinasi dari pendekatan GGX dan Schlick-Beckmann, dan dikenal sebagai Schlick-GGX:

$$

$$G_ {SchlickGGX} (n, v, k) = \ frac {n \ cdot v} {(n \ cdot v) (1 - k) + k}$$

Di sini $$$k$ adalah desain ulang $$$\ alpha$ tergantung pada apakah kita menggunakan fungsi geometri untuk penerangan langsung atau pencahayaan IBL:

$$

$$k_ {direct} = \ frac {(\ alpha + 1) ^ 2} {8}$$

$$

$$k_ {IBL} = \ frac {\ alpha ^ 2} {2}$$

Harap diperhatikan bahwa nilainya $$$\ alpha$ dapat bervariasi tergantung pada bagaimana mesin Anda menerjemahkan kekasaran $$$\ alpha$ . Dalam pelajaran berikut kita akan membahas secara rinci bagaimana dan di mana penugasan kembali ini menjadi relevan.

Untuk memperkirakan geometri secara efektif, kita harus memperhitungkan arah pandangan (geometri yang tumpang tindih) dan vektor arah cahaya (bayangan geometri sendiri). Kami dapat mempertimbangkan kedua kasus menggunakan metode Smith :

$$

$$G (n, v, l, k) = G_ {sub} (n, v, k) G_ {sub} (n, l, k)$$

Menggunakan Metode Smith dengan Schlick-GGX sebagai $$$G_ {sub}$ memberikan gambar berikut dengan kekasaran yang berbeda R:

Fungsi geometri adalah faktor antara [0,0, 1.0], di mana putih (atau 1.0) berarti tidak ada naungan pada permukaan mikro, dan hitam (atau 0,0) berarti naungan penuh pada permukaan mikro.

Dalam GLSL, fungsi geometri dikonversi ke kode berikut:

 float GeometrySchlickGGX(float NdotV, float k) { float nom = NdotV; float denom = NdotV * (1.0 - k) + k; return nom / denom; } float GeometrySmith(vec3 N, vec3 V, vec3 L, float k) { float NdotV = max(dot(N, V), 0.0); float NdotL = max(dot(N, L), 0.0); float ggx1 = GeometrySchlickGGX(NdotV, k); float ggx2 = GeometrySchlickGGX(NdotL, k); return ggx1 * ggx2; } 

Persamaan Fresnel

Persamaan Fresnel menggambarkan rasio cahaya yang dipantulkan dan dibiaskan, yang tergantung pada sudut di mana kita melihat permukaan. Ketika cahaya menyentuh permukaan, persamaan Fresnel memberi kita persentase cahaya yang dipantulkan berdasarkan sudut di mana kita melihat permukaan ini. Dari rasio refleksi dan hukum kekekalan energi ini, kita dapat langsung memperoleh bagian cahaya yang dibiaskan, yang akan sama dengan energi yang tersisa.

Setiap permukaan atau bahan memiliki tingkat reflektifitas dasar , diamati ketika melihat permukaan secara langsung, tetapi jika Anda melihat permukaan secara miring, semua pantulan menjadi lebih terlihat. Anda dapat memverifikasinya sendiri dengan melihat meja kayu atau logam Anda terlebih dahulu secara tegak lurus dan kemudian pada sudut mendekati 90 derajat. Anda akan melihat bahwa refleksi menjadi jauh lebih terlihat. Semua permukaan, secara teoritis, sepenuhnya memantulkan cahaya jika dilihat dari mereka pada sudut ideal 90 derajat. Efek ini dinamai Fresnel dan dijelaskan oleh persamaan Fresnel .

Persamaan Fresnel cukup kompleks, tetapi, untungnya, dapat disederhanakan menggunakan pendekatan Fresnel-Schlick :

$$

$$F_ {Schlick} (j, v, F_0) = F_0 + (1 - F_0) (1− (h \ cdot v)) ^ 5$$

$$$F_0$ mewakili reflektifitas dasar permukaan, yang kita hitung menggunakan sesuatu yang disebut indeks bias atau IOR (indeks bias), dan, seperti yang dapat Anda lihat pada permukaan bola, semakin dekat arah penglihatan ke batas bola yang terlihat (sudut antara arah penglihatan dan median) 90 ), , , :

, . , - . (), , . , ( $$$F_0$ ) ( 0 , ) -, , .

. , , :

: 0.17, , , ( ) 0.5 1.0. , “”, $$$F_0$ RGB ( ).

, metallic workflow: , (metalness), , .

: , ; , . , 0.0 1.0. - , , , . , .

$$$F_0$ , , - , , . :

 vec3 F0 = vec3(0.04); F0 = mix(F0, surfaceColor.rgb, metalness); 

, . , $$$F_0$ . 0.04 . , , , F0 . , , .

- :

 vec3 fresnelSchlick(float cosTheta, vec3 F0) { return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0); } 

cosTheta .

-

BRDF - :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+k_s\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

. , , F . $$$k_s$ , , $$$k_s$ . , :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

, PBR. , , . , , .

PBR

, PBR, , , PBR. , PBR, . , : , .

, PBR, :

: , . , . , ; .

: , , . , , .

: . , PBR-, , : .

: , . . , . PBR- , , (1.0 — ) .

AO (ambient occlusion) : AO . , , . AO , . . , 3D-.

. PBR, , . , PBR, PBR-, , , .

• Background: Physics and Math of Shading by Naty Hoffmann: , , ; PBR, must-read .
• Real shading in Unreal Engine 4 : PBR, Epic Games Unreal Engine 4. PBR, , .
• Marmoset: PBR Theory : PBR. , , , .
• Coding Labs: Physically based rendering : , PBR.
• Coding Labs: Physically Based Rendering — Cook–Torrance : BRDF -
• Wolfire Games — Physically based rendering : PBR Lukas Orsvärn.
• [SH17C] Physically Based Shading : shadertoy (: ) Krzysztof Narkowi, PBR.