Prinsip tindakan paling tidak. Bagian 2

Terakhir kali kami memeriksa secara singkat salah satu prinsip fisik yang paling luar biasa - prinsip tindakan paling tidak, dan mengambil contoh yang, tampaknya, bertentangan dengan itu. Dalam artikel ini, kita akan membahas prinsip ini lebih terinci dan melihat apa yang terjadi dalam contoh ini.

Kali ini kita perlu sedikit matematika lagi. Namun, saya akan mencoba untuk mengatur bagian utama artikel lagi di tingkat dasar. Saya akan menyoroti poin yang sedikit lebih ketat dan kompleks, mereka dapat dilewati tanpa mengurangi pemahaman dasar artikel.

Kondisi batas

Kita akan mulai dengan objek paling sederhana - bola bergerak bebas di ruang angkasa, di mana tidak ada gaya yang bekerja. Bola seperti itu, seperti diketahui, bergerak secara seragam dan lurus. Untuk kesederhanaan, anggap itu bergerak di sepanjang sumbu $$$x$ :

Untuk menggambarkan gerakannya secara akurat, sebagai aturan, kondisi awal ditentukan. Misalnya, ditentukan pada saat awal waktu $$$t_A$ bola ada di suatu titik $$$A$ dengan koordinat $$$x_A$ dan memiliki kecepatan $$$v_A$ . Setelah menetapkan kondisi awal dalam formulir ini, kami secara unik menentukan pergerakan bola lebih lanjut - bola akan bergerak dengan kecepatan konstan, dan posisinya pada saat itu $$$t$ akan sama dengan posisi awal ditambah kecepatan dikalikan dengan waktu yang telah berlalu: $$$x (t) = x_A + v_A \ cdot (t-t_A)$ . Cara mengatur kondisi awal ini sangat alami dan akrab secara intuitif. Kami menanyakan semua informasi yang diperlukan tentang gerakan bola pada saat awal, dan kemudian gerakannya ditentukan oleh hukum Newton.

Namun, ini bukan satu-satunya cara untuk menentukan pergerakan bola. Cara alternatif lain adalah mengatur posisi bola pada dua titik waktu yang berbeda. $$$t_A$ dan $$$t_B$ . Yaitu tanyakan itu:

1) tepat waktu $$$t_A$ bola ada di suatu titik $$$A$ (dengan koordinat $$$x_A$ );
2) tepat waktu $$$t_B$ bola ada di suatu titik $$$B$ (dengan koordinat $$$x_B$ )

Ekspresi "pada suatu titik $$$A$ "Tidak berarti bola beristirahat pada suatu titik $$$A$ . Tepat waktu $$$t_A$ dia bisa terbang di suatu titik $$$A$ . Artinya posisinya tepat waktu $$$t_A$ bertepatan dengan titik $$$A$ . Hal yang sama berlaku pada intinya $$$B$ .

Kedua kondisi ini juga secara unik menentukan pergerakan bola. Gerakannya mudah dihitung. Untuk memenuhi kedua kondisi, kecepatan bola jelas harus $$$(x_B-x_A) / (t_B-t_A)$ . Posisi bola tepat waktu $$$t$ lagi akan sama dengan posisi awal ditambah kecepatan dikalikan dengan waktu yang telah berlalu:

$$

$$x (t) = x_A + ((x_B-x_A) / (t_B-t_A)) \ cdot (t-t_A)$$

Perhatikan bahwa dalam kondisi masalah kita tidak perlu mengatur kecepatan awal. Ini ditentukan secara unik dari kondisi 1) dan 2).

Pengaturan kondisi dengan cara kedua terlihat tidak biasa. Mungkin tidak jelas mengapa secara umum mungkin perlu untuk meminta mereka dalam formulir ini. Namun, dalam prinsip tindakan paling tidak, justru kondisi dalam bentuk 1) dan 2) yang digunakan, dan bukan dalam bentuk pengaturan posisi awal dan kecepatan awal.

Lintasan aksi terkecil

Sekarang mari kita sedikit menyimpang dari gerakan bebas bola yang sebenarnya dan pertimbangkan masalah matematika murni berikut ini. Misalkan kita memiliki bola yang bisa kita gerakkan secara manual dengan cara apa pun yang kita inginkan. Dalam hal ini, kita perlu memenuhi ketentuan 1) dan 2). Yaitu di antara keduanya $$$t_A$ dan $$$t_B$ kita harus memindahkannya dari titik $$$A$ to the point $$$B$ . Ini dapat dilakukan dengan cara yang sangat berbeda. Setiap metode tersebut akan disebut lintasan bola dan dapat dijelaskan oleh fungsi dari posisi bola $$$x (t)$ . Mari kita tunda beberapa lintasan ini pada grafik ketergantungan posisi bola tepat waktu:

Misalnya, kita bisa memindahkan bola dengan kecepatan yang sama dengan $$$(x_B-x_A) / (t_B-t_A)$ (jalur hijau). Atau kita bisa menyimpannya di setengah titik $$$A$ dan kemudian gandakan kecepatan untuk pindah ke titik $$$B$ (lintasan biru). Pertama-tama Anda dapat memindahkannya ke arah yang berlawanan. $$$B$ samping dan kemudian sudah pindah ke $$$B$ (lintasan coklat). Anda bisa memindahkannya bolak-balik (lintasan merah). Secara umum, Anda dapat memindahkannya sesuka Anda, jika hanya kondisi 1) dan 2) yang diamati.

Untuk setiap lintasan seperti itu, kami dapat mencocokkan nomor. Dalam contoh kita, mis. dengan tidak adanya kekuatan yang bekerja pada bola, jumlah ini sama dengan total energi kinetik yang terakumulasi untuk seluruh waktu pergerakannya dalam interval antara $$$t_A$ dan $$$t_B$ dan disebut tindakan.

Dalam hal ini, kata "akumulasi" energi kinetik tidak secara akurat menyampaikan artinya. Pada kenyataannya, energi kinetik tidak menumpuk di mana pun, akumulasi hanya digunakan untuk menghitung tindakan lintasan. Dalam matematika, untuk akumulasi seperti itu ada konsep yang sangat bagus - integral:

$$

$$S = \ int \ limit_ {t_A} ^ {t_B} Tdt$$

Tindakan biasanya ditunjukkan oleh surat itu $$$S$ . Simbol $$$T$ berarti energi kinetik. Integral ini berarti bahwa tindakannya sama dengan akumulasi energi kinetik bola selama periode waktu dari $$$t_A$ sebelumnya $$$t_B$ .

Sebagai contoh, mari kita ambil bola seberat 1 kg., Tetapkan beberapa kondisi batas dan hitung aksi untuk dua lintasan yang berbeda. Biarkan intinya $$$B$ berjarak 1 meter dari titik tersebut $$$A$ dan waktu $$$t_B$ jauh dari waktu $$$t_A$ selama 1 detik. Yaitu kita harus menggerakkan bola yang pada saat awal berada di titik $$$A$ , dalam satu detik pada jarak 1 m di sepanjang sumbu $$$x$ .

Pada contoh pertama (lintasan hijau) kami menggerakkan bola secara merata, mis. dengan kecepatan yang sama, yang, jelas, harus sama dengan: $$$v = 1$ m / s Energi kinetik bola pada setiap saat waktu sama dengan: $$$T = mv ^ 2/2$ = 1/2 J. Dalam satu detik, 1/2 J akan menumpuk $$$\ cdot$ dengan energi kinetik. Yaitu valid untuk lintasan tersebut adalah: $$$S = 1/2$ J $$$\ cdot$ s

Sekarang jangan langsung mentransfer bola dari titik $$$A$ to the point $$$Ke$ , dan tahan pada satu titik selama setengah detik $$$A$ , dan kemudian, untuk sisa waktu, kami mentransfernya secara merata ke titik $$$B$ . Di babak pertama kedua, bola diam dan energi kinetiknya nol. Oleh karena itu, kontribusi pada aksi bagian lintasan ini juga sama dengan nol. Untuk babak kedua kami mentransfer bola dengan kecepatan ganda: $$$v = 2$ m / s Energi kinetik akan sama dengan $$$T = mv ^ 2/2$ = 2 J. Kontribusi periode waktu ini untuk tindakan akan 2 J dikalikan setengah detik, yaitu 1 J $$$\ cdot$ s Oleh karena itu, tindakan umum untuk lintasan tersebut sama dengan $$$S = 1$ J $$$\ cdot$ s

Demikian pula, lintasan lain dengan kondisi batas yang ditentukan 1) dan 2) sesuai dengan angka tertentu yang sama dengan tindakan untuk lintasan yang diberikan. Di antara semua lintasan tersebut, ada lintasan di mana tindakannya adalah yang paling sedikit. Dapat dibuktikan bahwa lintasan ini adalah lintasan hijau, yaitu pergerakan bola yang seragam. Untuk lintasan lain, tidak peduli seberapa rumitnya, tindakannya akan lebih dari 1/2.

Dalam matematika, perbandingan semacam itu untuk setiap fungsi dari angka tertentu disebut fungsional. Cukup sering dalam fisika dan matematika, tugas-tugas seperti kita muncul, yaitu untuk menemukan fungsi yang nilai fungsional tertentu minimal. Sebagai contoh, salah satu tugas sejarah yang sangat penting untuk pengembangan matematika adalah masalah bachistochrone . Yaitu menemukan kurva di mana bola menggulung tercepat. Sekali lagi, setiap kurva dapat diwakili oleh fungsi h (x), dan setiap fungsi dapat diberi nomor, dalam hal ini waktu pengguliran bola. Sekali lagi, masalahnya bermula untuk menemukan fungsi yang nilai fungsionalnya minimal. Area matematika yang berurusan dengan masalah seperti itu disebut kalkulus variasi.

Prinsip tindakan paling tidak

Dalam contoh yang dibahas di atas, kami memiliki dua lintasan khusus yang diperoleh dengan dua cara berbeda.

Lintasan pertama diperoleh dari hukum fisika dan sesuai dengan lintasan nyata bola bebas, yang tidak terpengaruh oleh gaya apa pun dan yang syarat batasnya diberikan dalam bentuk 1) dan 2).

Lintasan kedua diperoleh dari masalah matematika untuk menemukan lintasan dengan syarat batas 1) dan 2), yang tindakannya minimal.

Prinsip tindakan paling tidak menyatakan bahwa kedua lintasan ini harus bersamaan. Dengan kata lain, jika diketahui bahwa bola bergerak sedemikian rupa sehingga kondisi batas 1) dan 2) terpenuhi, maka bola tersebut harus bergerak di sepanjang jalan yang tindakannya minimal dibandingkan dengan jalur lain dengan kondisi batas yang sama.

Orang mungkin menganggap ini hanya kebetulan. Ada banyak masalah di mana lintasan seragam dan garis lurus muncul. Namun, prinsip aksi paling tidak adalah prinsip yang sangat umum, berlaku dalam situasi lain, misalnya, untuk pergerakan bola dalam medan gravitasi yang seragam. Untuk melakukan ini, Anda hanya perlu mengganti energi kinetik dengan perbedaan energi kinetik dan potensial. Perbedaan ini disebut fungsi Lagrangian atau Lagrange dan tindakan sekarang menjadi sama dengan total akumulasi Lagrangian. Bahkan, fungsi Lagrange berisi semua informasi yang diperlukan tentang sifat dinamis sistem.

Jika kita meluncurkan bola di medan gravitasi yang seragam sehingga melewati titik $$$A$ pada waktu $$$t_A$ dan terbang ke titik $$$B$ pada waktu $$$t_B$ , maka dia, menurut hukum Newton, akan menerbangkan parabola. Parabola inilah yang bertepatan dengan lintasan yang tindakannya minimal.

Jadi, untuk benda yang bergerak di medan potensial, misalnya, di medan gravitasi Bumi, fungsi Lagrange sama dengan: $$$L = T (v) -V (x, y, z)$ . Energi kinetik $$$T$ tergantung pada kecepatan tubuh, dan potensi - pada posisinya, mis. koordinat $$$x, y, z$ . Dalam mekanika analitik, seluruh rangkaian koordinat yang menentukan posisi suatu sistem biasanya dilambangkan dengan satu huruf $$$q$ . Untuk bola yang bergerak bebas di medan gravitasi, $$$q$ berarti koordinat $$$x$ , $$$y$ dan $$$z$ .

Untuk menunjukkan tingkat perubahan kuantitas, dalam fisika sangat sering mereka hanya mengakhiri kuantitas ini. Sebagai contoh $$$\ dot x$ menunjukkan tingkat perubahan koordinat $$$x$ , atau, dengan kata lain, kecepatan tubuh dalam arah $$$x$ . Menggunakan konvensi ini, kecepatan bola kami dalam mekanika analitik dilambangkan sebagai $$$\ dot q$ . Yaitu $$$\ dot q$ komponen kecepatan rata-rata $$$v_x, v_y, v_z$ .

Karena fungsi Lagrange tergantung pada kecepatan dan koordinat, itu juga dapat secara eksplisit tergantung pada waktu (secara eksplisit tergantung pada waktu berarti bahwa nilai $$$L$ pada titik yang berbeda dalam waktu, berbeda, pada kecepatan dan posisi bola yang sama) maka aksi dalam bentuk umum ditulis sebagai

$$

$$S = \ int \ limit_ {t_A} ^ {t_B} L (\ dot q, q, t) dt$$

Tidak selalu minimal

Namun, pada akhir bagian sebelumnya, kami melihat contoh di mana prinsip tindakan paling tidak jelas tidak bekerja. Untuk melakukan ini, kami kembali mengambil bola gratis, yang tidak terpengaruh oleh kekuatan apa pun, dan menempatkan dinding pegas di sebelahnya.
Kami mengatur kondisi batas sedemikian rupa sehingga titik $$$A$ dan $$$B$ cocok Yaitu dan tepat waktu $$$t_A$ dan tepat waktu $$$t_B$ bola harus berada di titik yang sama $$$A$ . Salah satu lintasan yang mungkin adalah berdiri bola di tempat. Yaitu sepanjang waktu antara $$$t_A$ dan $$$t_B$ dia akan berdiri pada suatu titik $$$A$ . Energi kinetik dan potensial dalam hal ini akan sama dengan nol, oleh karena itu aksi lintasan seperti itu juga akan sama dengan nol.

Sebenarnya, energi potensial dapat diambil tidak sama dengan nol, tetapi untuk jumlah berapa pun, karena perbedaan energi potensial pada titik-titik berbeda dalam ruang adalah penting. Namun, perubahan nilai energi potensial tidak memengaruhi pencarian lintasan dengan tindakan minimal. Hanya saja untuk semua lintasan nilai tindakan akan berubah dengan angka yang sama, dan lintasan dengan tindakan minimal akan tetap lintasan dengan tindakan minimal. Untuk kenyamanan, untuk bola kami, kami akan memilih energi potensial yang sama dengan nol.

Lintasan fisik lain yang mungkin dengan kondisi batas yang sama adalah lintasan di mana bola pertama kali terbang ke kanan, melewati titik $$$A$ pada waktu $$$t_A$ . Kemudian ia bertabrakan dengan pegas, mengompresnya, pegas, meluruskan, mendorong bola kembali, dan sekali lagi ia terbang melewati titik $$$A$ . Anda dapat memilih kecepatan bola sehingga, memantul dari dinding, terbang satu poin $$$A$ tepat pada saat ini $$$t_B$ . Tindakan dengan lintasan ini pada dasarnya akan sama dengan akumulasi energi kinetik selama penerbangan antara titik $$$A$ dan dinding dan kembali. Akan ada periode waktu tertentu ketika bola menekan pegas dan energi potensinya meningkat, dan selama periode waktu ini energi potensial akan memberikan kontribusi negatif pada aksi. Tetapi jangka waktu seperti itu tidak akan terlalu besar dan tindakannya tidak akan banyak berkurang.



Angka tersebut menunjukkan lintasan bola yang mungkin secara fisik mungkin. Jalur hijau sesuai dengan bola saat istirahat, sedangkan biru sesuai dengan bola memantul dari dinding pegas.

Namun, hanya satu dari mereka yang memiliki efek minimal, yaitu yang pertama! Lintasan kedua memiliki lebih banyak aksi. Ternyata dalam masalah ini ada dua lintasan yang mungkin secara fisik dan hanya satu dengan tindakan minimal. Yaitu dalam hal ini, prinsip tindakan paling tidak tidak berhasil.

Poin stasioner

Untuk memahami apa yang terjadi di sini, mari kita menyimpang dari prinsip tindakan paling tidak untuk saat ini dan menjalankan fungsi yang biasa. Mari kita fungsi $$$y (x)$ dan menggambar jadwalnya:

Pada grafik, saya menandai empat titik khusus berwarna hijau. Apa yang umum pada poin-poin ini? Bayangkan bahwa grafik fungsi adalah slide nyata tempat bola bisa bergulir. Keempat titik yang ditandai istimewa karena jika Anda memasang bola tepat pada titik ini, ia tidak akan menggelinding ke mana pun. Di semua titik lain, misalnya, titik E, ia tidak akan dapat tetap di tempatnya dan akan mulai meluncur ke bawah. Poin seperti itu disebut stasioner. Menemukan poin seperti itu adalah tugas yang bermanfaat, karena maksimum atau minimum dari fungsi, jika tidak memiliki ketajaman tajam, harus menjadi titik stasioner.

Jika kita lebih akurat mengklasifikasikan titik-titik ini, maka titik A adalah minimum absolut dari fungsi, yaitu nilainya kurang dari nilai fungsi lainnya. Titik B - tidak maksimum atau minimum dan disebut titik pelana. Titik C disebut maksimum lokal, mis. nilai di dalamnya lebih besar dari pada titik-titik tetangga dari fungsi. Dan titik D adalah minimum lokal, mis. nilai di dalamnya kurang dari pada titik-titik tetangga dari fungsi.

Pencarian untuk titik-titik tersebut dilakukan oleh cabang matematika yang disebut analisis matematika. Dengan cara lain, kadang-kadang disebut analisis infinitesimal, karena ia tahu cara bekerja dengan jumlah yang sangat kecil. Dari sudut pandang analisis matematis, titik-titik stasioner memiliki satu sifat khusus, terima kasih yang dapat ditemukan. Untuk memahami properti ini, kita perlu memahami seperti apa fungsi itu pada jarak yang sangat kecil dari titik-titik ini. Untuk melakukan ini, kami mengambil mikroskop dan melihatnya pada titik kami. Gambar tersebut menunjukkan seperti apa fungsi di sekitar berbagai titik pada perbesaran berbeda.

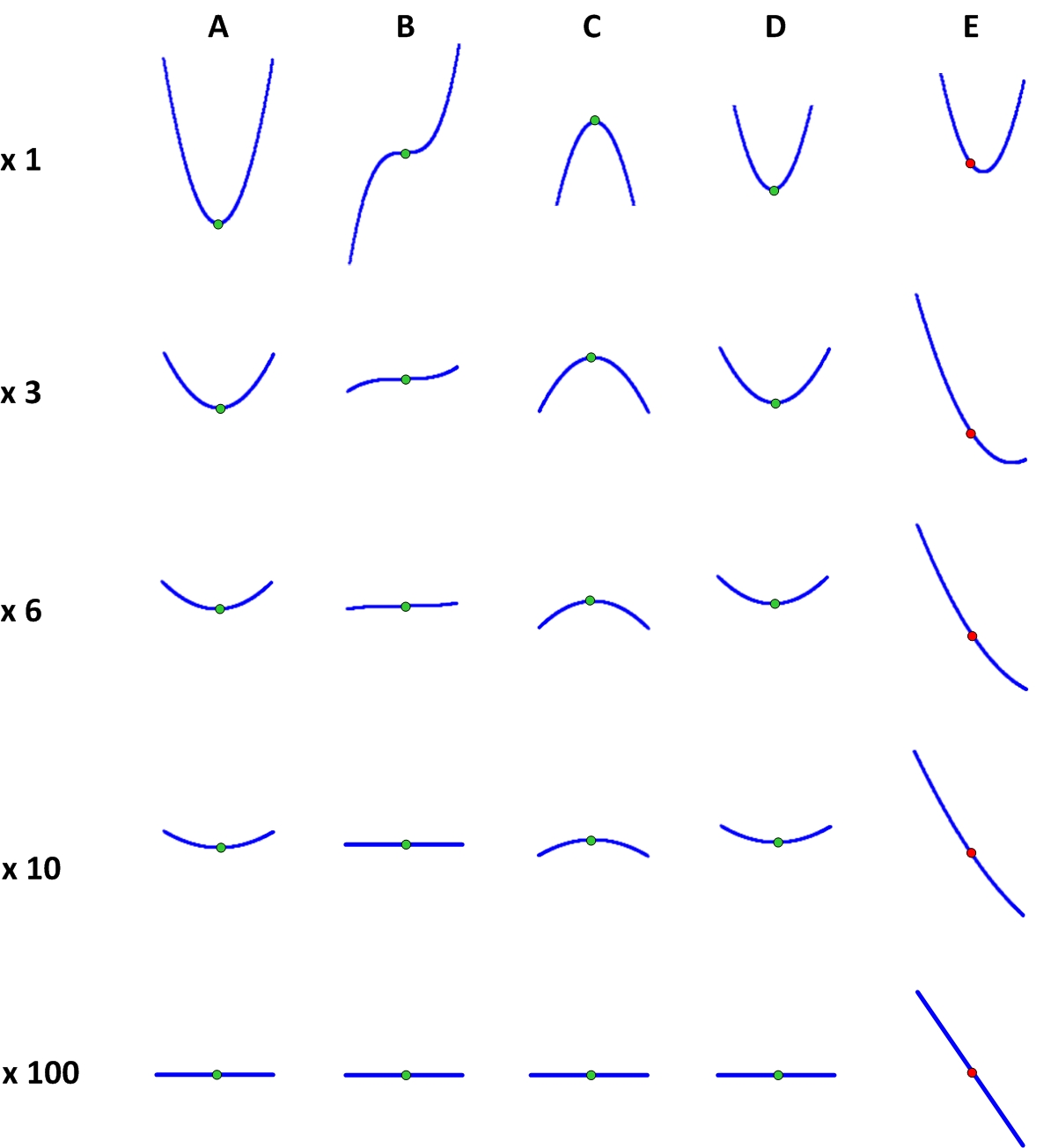
Dapat dilihat bahwa pada perbesaran yang sangat besar (mis., Pada penyimpangan yang sangat kecil x), titik-titik diam tampak persis sama dan sangat berbeda dari titik tidak-diam. Sangat mudah untuk memahami apa perbedaan ini: grafik fungsi pada titik stasioner dengan kenaikan menjadi garis horizontal yang ketat, dan pada non stasioner ia menjadi garis miring. Itulah sebabnya bola yang dipasang pada titik diam tidak akan berguling.

Horisontalitas fungsi pada titik stasioner dapat diekspresikan secara berbeda: fungsi pada titik stasioner secara praktis tidak berubah dengan perubahan yang sangat kecil dalam argumennya. $$$x$ , bahkan dibandingkan dengan argumen itu sendiri. Fungsi ini pada titik non-stasioner dengan perubahan kecil $$$x$ bervariasi sesuai proporsi $$$x$ . Dan semakin besar sudut fungsi, semakin kuat fungsinya berubah saat berubah $$$x$ . Bahkan, fungsi dengan ukuran bertambah menjadi lebih dan lebih mirip dengan garis singgung ke grafik pada titik tersebut.

Dalam bahasa matematika yang ketat, ungkapan “fungsi praktis tidak berubah pada suatu titik $$$x_0$ dengan sedikit perubahan $$$x$ "Berarti rasio perubahan fungsi dan perubahan argumennya $$$Δy / Δx$ cenderung 0 pada $$$∆x$ cenderung ke 0:

$$$$ menampilkan $$ \ lim_ {Δx \ hingga 0} \ frac {Δy (x_0)} {Δx} = \ lim_ {x \ hingga 0} \ frac {y (x_0 + Δx) -y (x_0) } {∆x} = 0 $$ tampilkan $$

Untuk titik non-stasioner, rasio ini cenderung ke angka bukan nol, yang sama dengan kemiringan fungsi pada titik ini. Angka yang sama disebut turunan dari fungsi pada titik tertentu. Turunan dari fungsi menunjukkan seberapa cepat fungsi berubah di dekat titik tertentu dengan sedikit perubahan dalam argumennya $$$x$ . Dengan demikian, titik stasioner adalah titik di mana turunan dari fungsi adalah 0.

Lintasan stasioner

Dengan analogi dengan titik-titik stasioner, konsep lintasan stasioner dapat diperkenalkan. Ingatlah bahwa setiap lintasan sesuai dengan nilai tindakan tertentu, mis. beberapa nomor. Kemudian bisa ada lintasan yang sedemikian sehingga untuk lintasan yang dekat dengannya dengan kondisi batas yang sama, nilai tindakan yang sesuai praktis tidak akan berbeda dari tindakan untuk lintasan stasioner itu sendiri. Lintasan seperti itu disebut stasioner. Dengan kata lain, lintasan apa pun yang dekat dengan stasioner akan memiliki nilai tindakan yang sedikit berbeda dari aksi lintasan stasioner ini.

Sekali lagi, dalam bahasa matematika "sedikit berbeda" memiliki arti yang tepat sebagai berikut. Katakanlah kita memiliki fungsional $$$S (x (t))$ untuk fungsi dengan syarat batas yang disyaratkan 1) dan 2), yaitu $$$x (t_A) = A$ dan $$$x (t_B) = B$ . Asumsikan bahwa lintasan $$$x (t)$ - stasioner.

Kita dapat mengambil fungsi lainnya. $$$g (t)$ sedemikian rupa sehingga pada akhirnya dibutuhkan nilai nol, yaitu $$$g (t_A)$ = $$$g (t_B)$ = 0. Juga ambil variabelnya $$$ε$ yang akan kita lakukan semakin sedikit. Dari kedua fungsi dan variabel ini $$$ε$ kita bisa membuat fungsi ketiga $$$x '(t) = x (t) + εg (t)$ , $$$f'(t_A)=A$ dan $$$f'(t_B)=B$ . $$$ε$ , $$$x'(t)$ , $$$x(t)$ .

$$$ε$ $$$x'(t)$ $$$x(t)$ $$$ε$ . Yaitu

$$

$$\lim_{ε \to 0} \frac {S(x'(t))-S(x(t))}ε=\lim_{ε \to 0} \frac {S(x(t)+εg(t))-S(x(t))}ε = 0$$

$$$g(t)$ , $$$g(t_A)$ = $$$g(t_B)$ = 0.

(, , ) $$$δS$ . «» « ».

$$$δS=0$ .

Metode menemukan fungsi stasioner (tidak hanya untuk prinsip aksi terkecil, tetapi juga untuk banyak masalah lainnya) ditemukan oleh dua ahli matematika - Euler dan Lagrange. Ternyata fungsi stasioner, yang fungsionalnya dinyatakan oleh integral mirip dengan aksi integral, harus memenuhi persamaan tertentu, yang sekarang disebut persamaan Euler-Lagrange.

Prinsip stasioner

Situasi dengan tindakan minimum untuk lintasan mirip dengan situasi dengan minimum untuk fungsi. Agar lintasan memiliki efek paling kecil, lintasan itu harus lintasan stasioner. Namun, tidak semua lintasan stasioner adalah lintasan dengan tindakan minimal. Misalnya, lintasan stasioner dapat memiliki tindakan minimal secara lokal. Yaituaksinya akan kurang dari lintasan lain yang berdekatan. Namun, di suatu tempat yang jauh mungkin ada lintasan lain yang tindakannya akan lebih sedikit.

Ternyata tubuh nyata mungkin tidak harus bergerak sepanjang lintasan dengan aksi paling sedikit. Mereka dapat bergerak di sepanjang rangkaian lintasan khusus yang lebih luas, yaitu lintasan stasioner. Yaitulintasan tubuh yang sebenarnya akan selalu diam. Karena itu, prinsip tindakan paling tidak lebih tepat disebut prinsip tindakan diam. Namun, menurut tradisi yang sudah ada, sering disebut prinsip tindakan paling tidak, yang menyiratkan tidak hanya minimalitas ini, tetapi juga stasioneritas lintasan.

Sekarang kita dapat menuliskan prinsip tindakan stasioner dalam bahasa matematika, seperti yang biasanya ditulis dalam buku teks:

$$

$$δS=δ\int\limits_{t_A}^{t_B} L(\dot q,q,t)dt = 0$$

.

Di sini $$$q$Apakah koordinat yang digeneralisasi, mis. satu set variabel yang secara unik menentukan posisi sistem.
$$$\dot q$ - laju perubahan koordinat umum.
$$$L(\dot q,q,t)$ - fungsi Lagrange, yang tergantung pada koordinat umum, kecepatannya dan, mungkin, waktu.
$$$S$ - tindakan yang tergantung pada lintasan spesifik sistem (mis. $$$q(t)$ )

Lintasan sebenarnya dari sistem adalah stasioner, mis. bagi mereka variasi tindakan$$$δS=0$ .

Jika kita kembali ke contoh dengan bola dan dinding elastis, maka penjelasan tentang situasi ini sekarang menjadi sangat sederhana. Mengingat syarat batas bahwa bola juga harus selama$$$t_A$ dan selama $$$t_B$ langsung ke intinya $$$A$ . . , . , , . .

( ) , .