Game menggunakan grafik matematika, bukan grafik

Di tangkapan layar ini, Anda disuguhkan permainan yang tampak biasa dengan grafis piksel. Namun, tidak semuanya begitu sederhana.

Relief bumi di tempat menyerupai sinusoid, dan peluru mirip dengan dua grafik simetris dari akar x.

Faktanya, segala sesuatu yang Anda lihat di layar dalam satu atau lain cara berkaitan dengan matematika, kurva matematika dan grafik.

Latar belakang

Suatu ketika, saat menonton video Saluran "Numberphile", saya menemukan materi video yang sangat menarik yang disebut "The Formula of Everything" .

Dalam video ini, rumus referensial mandiri Tapper disajikan, yang, dengan nilai k tertentu, menciptakan kembali gambarnya pada grafik. Rumus ini terlihat seperti ini:

$$

$$\ frac {1} {2} <\ lfloor mod (\ lfloor \ frac {y} {17} \ rfloor 2 ^ {-17 \ lfloor x \ rfloor - mod (\ lfloor y \ rfloor, 17)}, 2 ) \ rfloor$$

Formula ini sangat menarik minat saya, dan saya punya ide:

"Dan bagaimana jika kamu membuat game di mana alih-alih tekstur biasa yang disimpan dalam berbagai file dalam format .png dan .jpg, grafik dan kurva matematika akan digunakan?"

Gagasan ini bagi saya agak menarik dan sulit diterapkan.

Tugasnya

Saya menghadapi tugas-tugas berikut:

• Munculkan arti game, gameplay
• Rumus yang diturunkan, grafik yang akan menjadi siluet karakter, peluru, permukaan yang saya butuhkan
• Terapkan semua ini dalam game

Gameplay dan makna permainan

Gameplay dan arti dari game berubah beberapa kali selama pengembangan game ini. Ini semua karena ada beberapa kesulitan, khususnya, dengan derivasi formula untuk siluet tertentu. Tetapi secara umum, game ini adalah tentang piring terbang kesepian yang terbang di sekitar planet, menjelajahi mereka dan membunuh musuh yang menghalangi jalannya.

Rumus dan implementasi selanjutnya dalam permainan

Saya telah menggabungkan dua paragraf berikut ke dalam satu subpos, karena tidak praktis untuk "melewati" antara satu formula dan implementasinya.

Untuk membuat game, bahasa pemrograman c ++ dan perpustakaan SFML dipilih untuk membuat windows dan menggambar sesuatu di atasnya.

Karena saya di sekolah dan baru-baru ini tahu apa itu sinusoid dan bagaimana tampilannya, saya punya masalah besar dalam menurunkan berbagai formula. Paling sering, ini berakhir dengan seleksi sederhana.

Di akhir artikel akan ada tautan ke GitHub, tempat semua kode diposting. Dalam artikel tersebut, hanya potongan kecil kode yang akan diberikan agar tidak membuang sampah sembarangan.

Permukaan planet

Untuk permukaan planet ini, saya memperoleh rumus berikut:

$$

$$f (x) = | sin (x) |$$

Formula yang cukup sederhana, tetapi ketika diimplementasikan, ada kebutuhan untuk mengontrol tinggi dan panjang sinusoid yang diberikan. Juga, untuk menghindari lengkungan relief, x dikalikan dengan π. Oleh karena itu, kode akhir terlihat seperti ini:

int groundC = ceil(abs(sin(((i+1)*groundScale*M_PI)))*groundHeight); 

Tekstur planet di ruang angkasa

Tekstur planet ini terdiri dari lingkaran dan pola di atasnya. Gim ini memiliki 4 formula untuk membuat pola dan 12 tekstur planet dengan pola yang berbeda. Bergantung pada "langkah" rumus, berbagai pola dibuat. Juga, saat membuat planet, diatur secara acak untuk warna, ukuran, dan posisi di ruang angkasa.

Peluru

Gambar peluru dari game. Peluru berbalik.

Untuk peluru, formula yang sangat sederhana dipilih:

$$

$$\ sqrt {x}$$

Alur formula ini dicerminkan pada absis.

Protagonis

Jadi kami sampai pada formula yang paling rumit.

Saya menyimpulkan formula protagonis dengan susah payah. Ini terlihat seperti ini:

$$

$$\ sqrt {x ^ {\ frac {1} {2.8}} + x ^ {10.9-x ^ {9.3-x}}}} - 0,3$$

Ya, formula yang sangat bengkok, sangat jelek. Tetapi yang utama bukanlah formula, hasil utamanya.

Untuk mencapai hasilnya, pada awalnya saya hanya ingin bergerak di sepanjang sumbu x dengan langkah tertentu, menuliskan koordinat y, dan kemudian menghubungkan semua titik ini, sehingga mendapatkan piring kami. Tapi kemudian, aku tidak sengaja mengambil langkah yang terlalu kecil, dan seluruh piringku dengan indahnya terkecuali dengan dua titik akhir, yang akhirnya terhubung. Hasilnya, pelat terlihat seperti ini:



Selanjutnya, kami membutuhkan tekstur protagonis di ruang angkasa. Ini terlihat seperti ini:



Itu didasarkan pada lingkaran. Kabin utama dibuat menggunakan rumus berikut:

$$

$$(x ^ {7-x}) ^ {\ frac {0.8} {x}}$$

Grafik formula ini dicerminkan di sepanjang sumbu ordinat.

Beginilah rumus ini terlihat di c ++:

 int x = round(pow(pow(i, 7 - i), 0.8 / i)); 

Musuh dan petelur mereka

Di sebelah kanan dalam gambar adalah spawner biru, benda merah adalah musuh.

Spauner adalah planet biasa dengan pola yang tidak biasa. Pola ini adalah grafik rumus:

$$

$$sin (x) * x ^ {0,8}$$

Formula Tekstur Musuh:

$$

$$(x ^ {3-x}) ^ {\ frac {1} {x}}$$

Pohon

Saya akui, saya tidak bisa mendapatkan atau memilih formula untuk membuat siluet pohon. Tapi, agar tidak melanggar konsep dasar seluruh permainan dan aturan untuk tidak menggunakan file berformat .png dan .jpg, saya menggunakan satu trik. Saya menggunakan fraktal untuk membuat pohon.


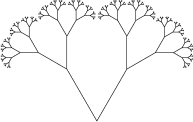Contoh pohon fraktal

Kemungkinan besar Anda akan setuju bahwa pohon fraktal sendiri terlihat cukup membosankan. Jika Anda menambahkan beberapa elemen keacakan, misalnya, 2 cabang mungkin tidak selalu tumbuh, tetapi juga 3 atau 1, atau tidak sama sekali. Juga, tidak mungkin membuat sudut kemiringan yang sama di mana-mana.

Tentu saja, orang bisa membuat pseudorand mesin biasa, yang didasarkan pada kutu komputer, tetapi ide berikut menurut saya lebih menarik:

"Dan bagaimana jika setiap pohon diberi nomor tertentu (benih) dari mana angka pseudo-acak akan dihitung yang mempengaruhi parameter pohon?"

Untungnya, c ++ memiliki pseudorandum library yang terpisah.

Akibatnya, pohon yang dihasilkan terlihat seperti ini:



Di sebelah kiri adalah pohon dengan biji 13, dan di sebelah kanan - 22

Dan kode yang menghasilkan pohon-pohon ini adalah:

 Branch Branch::createNewBranch(Branch cur, Tree* parent, float angleMultiplier, int level) { Vector2f sp(cur.startPoint.x, cur.startPoint.y); float randomAngle = ((*parent).getRand() * 15) - 5; float t = cur.thickness * 0.75; float l = cur.length * 0.67; float a = cur.angle + 30*angleMultiplier + randomAngle; sp.y -= (cos((cur.angle-180)*3.1415926 / 180) * cur.length); sp.x += (sin((cur.angle-180)*3.1415926 / 180) * cur.length); Branch gen(sp, t, l, a, level); if (level > 0) { int count = 100 * (*parent).getRand(); if (count >= 25 && count < 80) { //     ,      && count < 80,        ,  . , -          20%  10%,  ,    count<90 (*parent).addBranch(gen.createNewBranch(gen, parent, 1, level - 1)); (*parent).addBranch(gen.createNewBranch(gen, parent, -1, level - 1)); } if (count >= 80) { //    ,    count >= 90 if (count % 2 == 0) { (*parent).addBranch(gen.createNewBranch(gen, parent, -1, level - 1)); } else { (*parent).addBranch(gen.createNewBranch(gen, parent, 1, level - 1)); } } } return gen; } 

Catatan Ya, saya tahu saya “hardcoded” beberapa variabel, tapi tolong jangan salahkan saya untuk ini. Saya pikir tidak masuk akal untuk membuat variabel konstan yang terpisah, yang pada prinsipnya hanya memengaruhi peluang membuat cabang baru.

Beberapa kode lagi

Di atas, saya memberikan kode hanya untuk menghasilkan tekstur. Dalam subtitle ini, saya akan menjelaskan kode permainan itu sendiri. Semua kode ada di GitHub, tautan ke proyek sudah selesai.

Pemain

Pemain memiliki dua metode pembaruan yang berbeda - spaceUpdate dan planetUpdate. Dengan demikian, spaceUpdate memperbarui pemain saat berada di luar angkasa, planetUpdate - saat berada di planet ini. Di planet ini, akselerasi dan kecepatan pemain dihitung. Bergantung pada akselerasi horizontal, sudut kemiringan plat berubah dari 30 derajat ke -30. Mendekati penghalang, kecepatan pemain berkurang. Hambatan semacam itu ada untuk sumbu x (0; mapSize.x) dan untuk sumbu y. Untuk sumbu y, segalanya sedikit lebih rumit. Ada ketinggian minimum, yang dihitung sebagai berikut: ketinggian minimum bumi diambil, ditambahkan ke ketinggian gelombang sinus dan ketinggian pohon ditambahkan. Ketinggian pohon dihitung dengan cara yang sangat sederhana - panjang awal cabang dikalikan dengan jumlah siklus yang dilakukan selama generasi pohon. Tidak ada batas atas - terbang keluar dari peta dari atas, pemain beralih ke spaceUpdate dan ruang ditarik.

SpaceUpdate beroperasi sebagai berikut: akselerasi dan kecepatan pemain dihitung. Selanjutnya, sudut rotasi pemain dihitung. Sudut dihitung sebagai berikut: jika akselerasi adalah nol, maka sudut dihitung relatif terhadap kecepatan pemain, jika tidak, relatif terhadap akselerasi. Selain itu, di ruang angkasa, pemain memiliki kemungkinan menembak. Pemotretan terjadi sebagai berikut - peluru dibuat dengan rotasi seperti pemain dan ditambahkan ke daftar. Saat memperbarui pemain di luar angkasa, setiap peluru dalam daftar ini juga diperbarui. Saat merender pemain, peluru juga ditarik. Juga, di ruang, hal-hal sedikit lebih rumit dengan penghalang. Ruang dibagi menjadi beberapa sektor, di setiap sektor 4 planet, total - 1 000 planet dan 25 000 sektor. Setiap sektor memiliki id unik. Jika sisa saat membagi 500 sama dengan 0 - ada penghalang kiri, jika sisanya 499 benar, jika ketika membagi 500 hasilnya 0 - batas atas hadir, jika 499 adalah yang atas. Jika tidak ada penghalang, maka saat terbang keluar dari frame pemain bergerak ke sektor yang sesuai.

Ruang

Saya sudah menguraikan sebagian besar, tetapi masih ada beberapa hal yang masih ada. Di masing-masing sektor ruang ada 4 planet. Ketika seorang pemain menekan tombol E, jika ia berjarak radius dari planet ini, maka pemain tersebut pindah ke planet ini.

Musuh

AI musuh sangat bodoh - jika ada pemain dalam radius visibilitas mereka, maka mereka cenderung menabraknya, dan ada sedikit kesalahan, sehingga jalur mereka cukup melengkung. Jika tidak ada pemain dalam radius visibilitas mereka, maka mereka akan dikirim ke petelur mereka.

Spawner

Di setiap sektor ruang ada 1 spawner. Spauners bisa berukuran berbeda. Ukuran memengaruhi visibilitas pemain. Jika pemain berada di zona visibilitas mereka, spawner menciptakan musuh setiap 5 detik, tetapi jumlah musuh tidak dapat melebihi 10.

Kesimpulan

Setelah menghabiskan sekitar satu minggu, saya membuat game yang tidak menggunakan file .png atau .jpg.

Tautan ke proyek di GitHub

Bagi mereka yang terlalu malas untuk mengunduh proyek dan menjalankan gim, video pendek tentang gim: