
Kami melanjutkan kenalan kami dengan bahasa pemrograman Julia yang sangat muda, namun luar biasa indah dan kuat. Beta enam tahun akhirnya berakhir, jadi sekarang Anda tidak perlu takut dengan perubahan sintaksis. Dan sementara semua orang berdebat apakah baik atau buruk untuk mulai mengindeks dari satu, komunitas gelisah secara aktif mengacaukan: perpustakaan baru keluar, yang lama sedang diperbarui, proyek-proyek serius mulai, dan siswa secara aktif mengajar bahasa ini di universitas. Jadi jangan ditinggalkan! Kami membuat teh lebih kuat, karena kami akan membuat kode malam ini!
Persiapan untuk bekerja
Di sini ada review kecil dalam bahasa Rusia, juga di hub ada kenalan dengan bahasa dan instruksi instalasi . Sekali lagi, dengan berfokus pada perlunya Kerangka Kerja Manajemen Windows , akan ada masalah dengan mengunduh paket.
Setelah memutakhirkan, JuliaPRO sekarang hanya mencakup Juno . Tapi saya pribadi lebih suka Jupyter : tidak ada masalah dengan itu di laptop, ditambah lagi nyaman untuk bekerja di browser dan segera membuat catatan dan formula, secara umum, ideal untuk membuat laporan, slide atau manual.
Menikah dengan Jupyter dan Julia 1.0.1 Ada beberapa paket untuk Julia, yang paling sukses di antaranya termasuk dalam Plot sebagai backend. Plots.jl - Plots.jl of Plots.jl : yaitu antarmuka untuk berbagai perpustakaan charting. Jadi, Plots.jl sebenarnya hanya menginterpretasikan perintah Anda dan kemudian membuat grafik menggunakan semacam perpustakaan grafik. Pustaka grafis latar belakang ini disebut backend. Bagian terbaiknya adalah Anda dapat menggunakan banyak pustaka grafik yang berbeda dengan sintaks Plots.jl , dan kita juga akan melihat bahwa Plots.jl menambahkan fitur baru ke masing-masing pustaka ini!
Instal paket grafikUntuk menginstal paket, jalankan perintah di REPL, Juno, atau Jupyter:
# Pkg.add("Plots") # 0.7.0 julia>] pkg>add Plots pkg>add GR pkg>add PyPlot pkg>add Gadfly pkg>add PlotlyJS pkg>add UnicodePlots
Anda tidak perlu menginstal semua paket, tetapi Anda harus tahu bahwa masing-masing memiliki karakteristik sendiri. Saya lebih suka plotlyjs () : meskipun tidak berbeda dalam kecepatan, ini sangat interaktif. Ada zoom, bergerak di sepanjang pesawat, serta kemampuan untuk menyimpan file, dan jika Anda menyimpan dokumen Jupyter sebagai html, semua fitur akan disimpan. Jadi, Anda dapat menambahkan ke situs atau membuat presentasi interaktif. Informasi lebih lanjut tentang halaman: Plot , Gadfly
Pola prima tak berujung
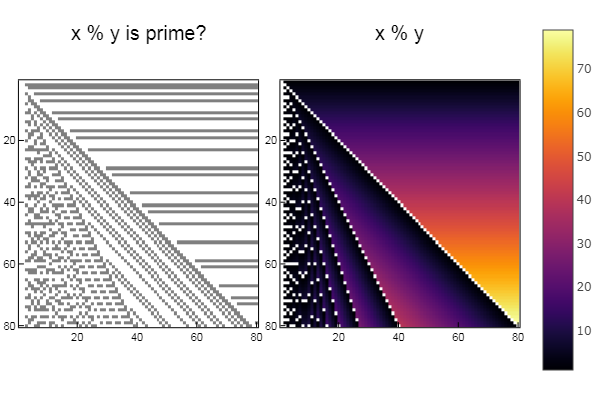
Menerapkan gagasan artikel tentang Habr . Dalam beberapa kata: bagaimana jika kita mengambil titik koordinat dan menggunakan operasi, katakanlah, XOR atau bitwise AND antara absis dan ordinat, dan kemudian periksa nomornya untuk kesederhanaan atau milik nomor Fibonacci, dan jika jawabannya ya, isi poin dengan satu warna, dan dengan yang negatif di yang lain? Periksa:
Untuk operasi% using Plots plotlyjs() function eratosphen(n, lst) # ar = [i for i=1:n] ar[1] = 0 for i = 1:n if ar[i] != 0 push!(lst, ar[i]) for j = i:i:n ar[j] = 0 end end end end ertsfn = [] eratosphen(1000, ertsfn) # print(ertsfn) # print( size(ertsfn) ) # -> 168 N = 80 M = 80 W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x % y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y is prime?") p2 = spy(W2, title = "x % y") plot(p1, p2, layout=(2),legend=false)
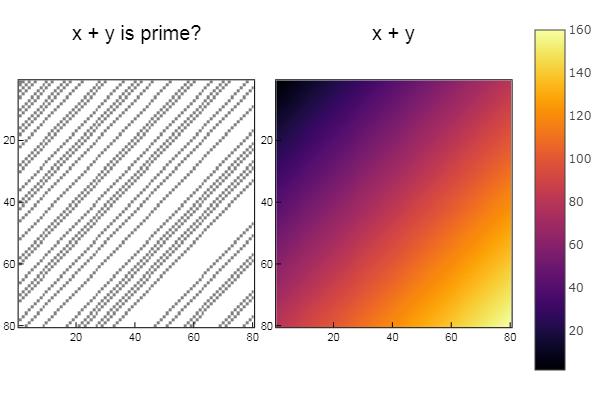
Untuk operasi + W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x + y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x + y is prime?") p2 = spy(W2, title = "x + y") plot(p1, p2, layout=(2),legend=false)
Untuk operasi | W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x | y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x | y is prime?") p2 = spy(W2, title = "x | y") plot(p1, p2, layout=(2),legend=false)

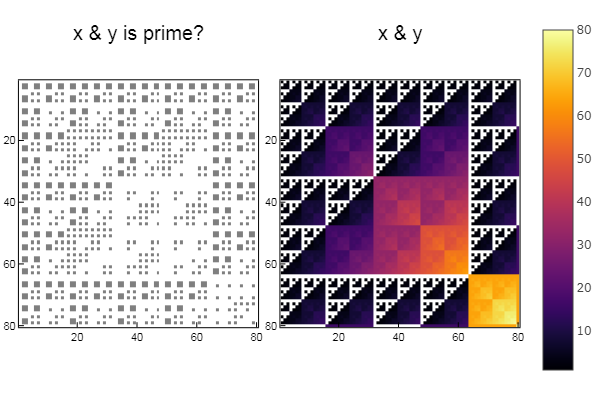
Untuk operasi & W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x & y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x & y is prime?") p2 = spy(W2, title = "x & y") plot(p1, p2, layout=(2),legend=false)
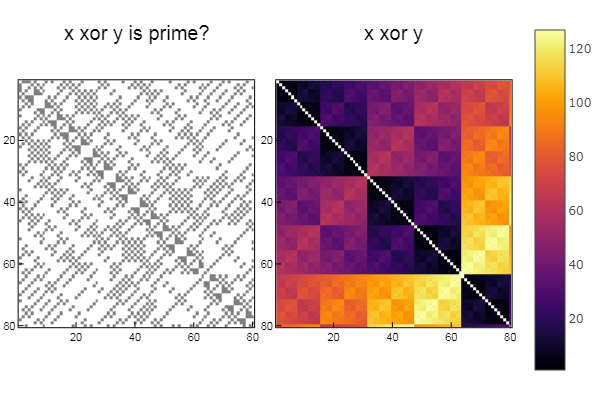
Untuk operasi xor W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M]; W2 = [xor(x, y) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y is prime?") p2 = spy(W2, title = "x xor y") plot(p1, p2, layout=(2),legend=false)
Dan sekarang semuanya sama, tetapi untuk angka FibonacciAnda dapat membuat seri seperti biasa dengan sesuatu seperti:
function fib(n) a = 0 b = 1 for i = 1:n a, b = b, a + b end return a end fbncc = fib.( [i for i=1:10] )
Tapi mari kita gunakan representasi matriks ( lebih terinci ):
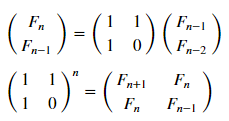
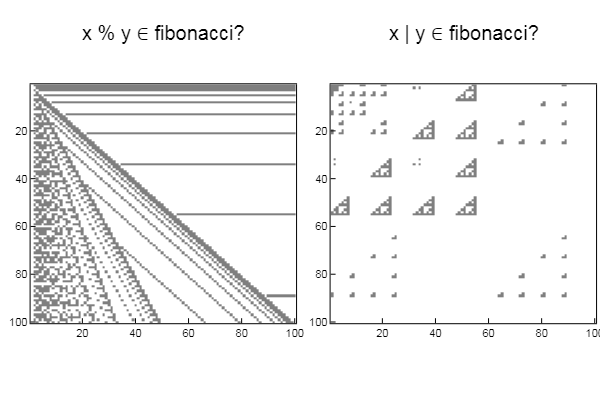
matr_fib = n -> [1 1; 1 0]^(n-1) # , n-1 mfbnc = [ matr_fib( i )[1,1] for i=1:17]; # 1,1 n- N = 100 M = N W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y ∈ fibonacci?") p2 = spy(W2, title = "x | y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
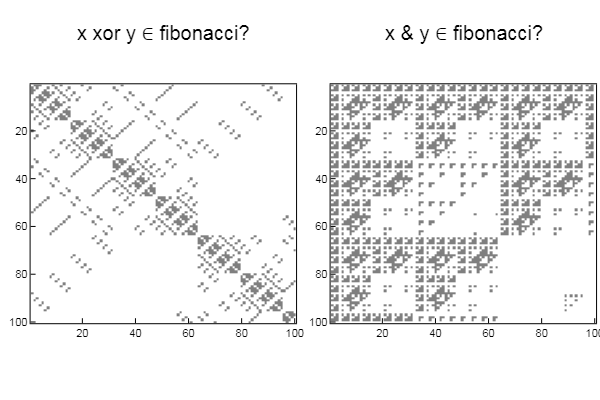
W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y ∈ fibonacci?") p2 = spy(W2, title = "x & y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
Refleksi sosok yang relatif lurus
Jenis tampilan ini ditentukan oleh matriks:
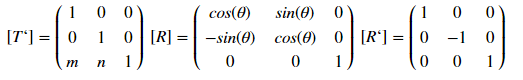
di mana [T '], [R] dan [R'], masing-masing, matriks perpindahan, rotasi dan refleksi. Bagaimana cara kerjanya? Mari kita analisis contoh offset - untuk titik dengan koordinat (x, y), offset oleh m demi x dan oleh n oleh game akan ditentukan oleh transformasi:
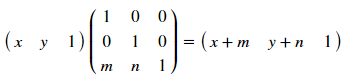
Matriks ini memungkinkan transformasi untuk berbagai poligon, yang utama adalah mencatat koordinat satu sama lain dan tidak melupakan kolom unit pada akhirnya. Jadi [T]:
- menggeser garis di titik asal bersamaan dengan poligon yang ditransformasikan
- putar untuk bertepatan dengan sumbu X
- mencerminkan semua titik poligon sehubungan dengan X
- diikuti oleh rotasi terbalik dan transfer
Topik ini dijelaskan lebih rinci dalam buku Rogers D., Adams J. Yayasan Matematika Grafik Komputer
Sekarang kode itu!
using Plots plotlyjs() f = x -> 0.4x + 2 # # X = [2 4 2 2]' Y = [4 6 6 4]' xs = [-2; 7] # ys = f(xs) inptmtrx = [ XY ones( size(X, 1), 1 ) ] # m = 0 n = -f(0) # Y displacement = [1 0 0; 0 1 0; mn 1] a = (ys[2]-ys[1]) / (xs[2]-xs[1]) # θ = -atan(a) rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1] reflection = [1 0 0; 0 -1 0; 0 0 1] T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) # outptmtrx = inptmtrx * T plot( X, Y) plot!( xs, ys ) plot!( outptmtrx[:,1], outptmtrx[:,2] )
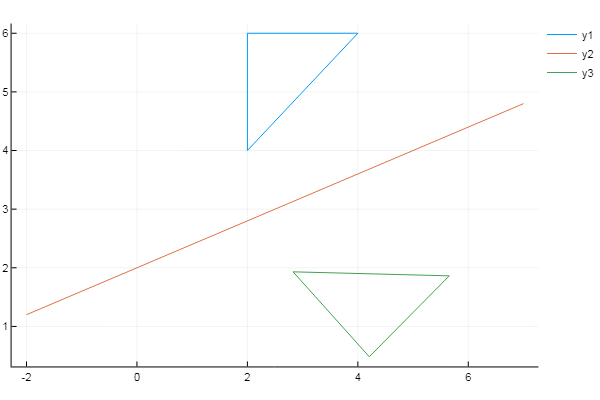
Fakta menarik: jika Anda menyingkirkan karakter Yunani dan ganti baris pertama dengan
function y=f(x,t) y=0.4*x + 2 endfunction,
Karena tanda kurung [] membingkai indeks array pada () , dan rakit pada plot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) ) , maka kode ini cukup banyak berjalan di Scilab .
Bekerja dengan grafik tiga dimensi
Beberapa paket ini mendukung pembuatan grafik tiga dimensi. Tapi saya ingin secara terpisah menyebutkan alat visualisasi Makie yang lebih kuat, yang bekerja bersama dengan paket GLFW dan GLAbstraction yang mengimplementasikan fitur OpenGL di julia. Informasi lebih lanjut tentang Makie . Kami menyembunyikan persetujuannya di bawah
spoiler using Makie N = 51 x = linspace(-2, 2, N) y = x z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4 scene = wireframe(x, y, z) xm, ym, zm = minimum(scene.limits[]) scene = surface!(scene, x, y, z) contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm)) scene
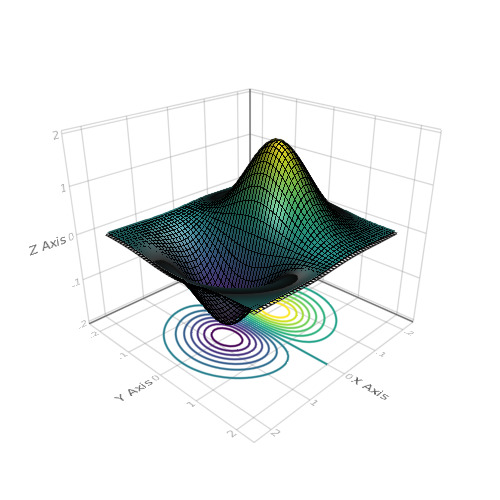
wireframe(Makie.loadasset("cat.obj"))

using FileIO scene = Scene(resolution = (500, 500)) catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh) mesh(catmesh, color = Makie.loadasset("diffusemap.tga"))

x = Makie.loadasset("cat.obj") mesh(x, color = :black) pos = map(x.vertices, x.normals) do p, n p => p .+ (normalize(n) .* 0.05f0) end linesegments!(pos, color = :blue)
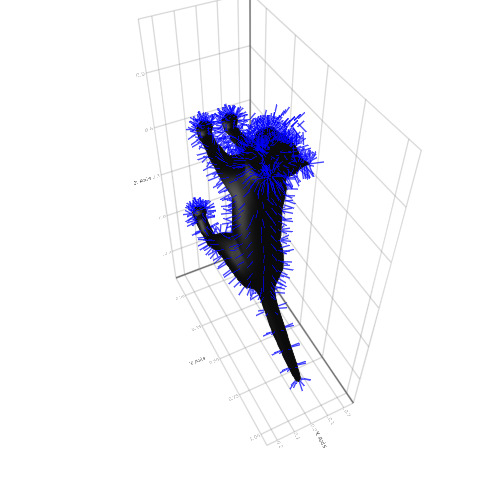
Itu semua dengan grafis. Interaktivitas, animasi, 3d, data besar atau pembuatan grafik sederhana yang cepat - paket yang terus berkembang akan memuaskan hampir semua selera dan kebutuhan, selain itu, semuanya sangat mudah dipelajari. Silakan mengunduh latihan praktis dan terus memahami Julia!
UPD: Semua daftar di atas dibuat di Jupyter dengan julia 0.6.4. Sayangnya, beberapa fungsi paket meta Plot dihapus atau diganti namanya, jadi kami terus memantau pembaruan, tetapi untuk saat ini mata-mata sepenuhnya diganti:
julia> using GR julia> Z = [x | y for x = 1:40, y = 1:40]; julia> heatmap(Z)