Membangun fungsi di konsol. Bagian 2 (Jadwal)

Mulai, dimulai



Terakhir kali saya memutuskan untuk membangun tabel nilai fungsi. Waktunya telah tiba untuk melanjutkan ke pembuatan jadwal itu sendiri, untuk mana semua ini, pada kenyataannya, dimulai.

Jadi, ide utamanya adalah sebagai berikut. Putar sumbu koordinat 90 derajat searah jarum jam. Ini diperlukan untuk menyederhanakan konstruksi tanpa menyimpan data tentang setiap titik di setiap lembar.

Selanjutnya, kami membatasi sumbu koordinat game menjadi 82 karakter untuk keterbacaan grafik yang lebih baik. Jelas bahwa dalam melakukannya kita kehilangan akurasi dan jadwal akan lebih skematis (terlalu ketat), terutama untuk fungsi "keren", tapi tetap saja.

Setelah itu, kita menghitung posisi sumbu x relatif terhadap sumbu pemain, yaitu, kita mencari di tempat mana kita akan memiliki titik (x, 0). Nah, maka kita akan menetapkan baris-demi-baris x nilai fungsi y1 pada titik ini.

Ayo pergi

Pertama, kita membutuhkan rumus berikut:

$$

$$rasio = (maks (y1) - min (y1)) / (80)$$

Kami akan menetapkan 80 posisi untuk jadwal itu sendiri, dua tempat yang tersisa akan murni dekoratif. Dengan rumus ini, kami menemukan rentang nilai mana yang sesuai dengan satu posisi di bagan kami. Kemudian kita dapat menandai titik saat ini dengan benar.

Gagasan utama diuraikan, jadi mari kita beralih ke kode itu sendiri

dial_length = 12 label = "  y1 = x**3 - 2*x**2 + 4*x - 8" print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 82, 'y' , 82*'-'])); 

Termasuk berkat komentar pada bagian pertama, saya belajar tentang hal seperti format . Bagiku itu terasa lebih nyaman daripada tarianku dengan rebana, jadi sepotong besar kode dari penghitungan indentasi berubah menjadi beberapa baris

 print("{1:>{0}}".format(len(label) + dial_length, label), '\n') 

Unit ini bertanggung jawab atas jumlah elemen yang diteruskan sebagai argumen ke fungsi format, yaitu, itu adalah "tautan" (tidak secara harfiah) ke variabel label, yang sebenarnya kami tampilkan di layar. Penomoran berjalan persis sama seperti di lembaran - dari awal.

Sepasang karakter :> digunakan untuk menyelaraskan teks yang ditampilkan di sisi kanan. Nah, {0} setelah karakter > diperlukan untuk menentukan jumlah posisi garis yang Anda butuhkan.

Yaitu, dalam hal ini, kami mencadangkan len label (label) + posisi dial_length, dan label itu sendiri hanya mengambil len (label), dan kami menyelaraskan teks di sisi kanan di dalam set posisi ini.

 print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print(dial_length*' ' + label, '\n') 

garis-garis ini setara


Ya, untuk string, mungkin lebih mudah menggunakan opsi kedua, tetapi menerapkan yang pertama untuk pengembangan umum tidak akan merugikan)

 print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 82, 'y' , 82*'-'])); 

Bahkan array tipe r_value (dalam C ++) dapat dijejalkan ke dalam format, yaitu, dibuat langsung ketika melewati argumen.

Kami memperbaiki variabel yang konstan dengan kami, yaitu, mereka tidak bergantung pada nilai fungsi saat ini.

Dalam python tidak ada konstanta kondisional untuk menunjuk konstanta, jadi sudah lazim untuk memanggil variabel-variabel semacam itu dalam huruf kapital dan tidak mengubahnya.

 MAX_Y1_VALUE_DIFFERENCE = (max_y1_value - min_y1_value) + \ (max_y1_value == min_y1_value) RATIO = MAX_Y1_VALUE_DIFFERENCE / 80 AXIS_X_POS = abs(int((- min_y1_value) / RATIO)) if (AXIS_X_POS > 80): AXIS_X_POS = 81 

Karena RATIO karena alasan yang jelas tidak boleh sama dengan 0, MAX_Y1_VALUE_DIFFERENCE harus berupa angka positif. Itulah mengapa istilah kedua ada di sisi kanan penugasan.

Posisi sumbu x yang kita hitung dengan rumus

$$

$$80 * (y1 (x) - min (y1)) / (maks (y1) - min (y1))$$

Dari mana formula ini berasal? Kami cukup menghitung rasio segmen (pada sumbu permainan) dari awal sumbu (min (y1)) ke nilai fungsi saat ini (y1 (x)) dan segmen dari awal sumbu hingga akhirnya (maks (y1)). Nah, kami mengalikan rasio ini dengan 80 untuk menemukan jarak dari awal sumbu ke nilai saat ini dalam spasi (oleh karena itu, Anda hanya dapat menggunakan bilangan bulat), yang akan mencerminkan rumus rasio pada grafik.

Karena kami tertarik pada posisi di y1 (x) = 0, kami mengganti nilai yang diperlukan dan voila ke dalam rumus.

Sekarang Anda dapat langsung menuju nilai pencetakan

 while (is_sequence_decreasing and from_x >= to_x) or \ (not is_sequence_decreasing and from_x <= to_x): y1_cur_value = y1(from_x) cur_y1_value_and_min_difference = (y1_cur_value - min_y1_value) + \ (y1_cur_value == min_y1_value) * \ ((max_y1_value == min_y1_value)) pos_of_y = int(cur_y1_value_and_min_difference * 80 / \ MAX_Y1_VALUE_DIFFERENCE) 

Siklusnya sudah tidak asing lagi bagi kita. Kita harus menghitung setiap nilai fungsi untuk kedua kalinya, agar tidak menyimpannya dalam lembar atau sesuatu yang lain.

Posisi permainan dihitung dengan rumus di atas.

Kita harus memperbaiki perbedaan atas dari rumus, menyediakan untuk kasus ketika dalam rumus kita mendapatkan ketidakpastian bentuk nol dengan nol. Jika ketidakpastian seperti itu muncul, itu berarti bahwa nilai saat ini adalah y1 (x) = maks (y1), yang berarti bahwa nilai saat ini dari permainan akan bertepatan dengan akhir sumbu y.

  print("{1:^{0}.6g}".format(dial_length, from_x), end='') if (negative_value_exists): if y1_cur_value <= 0 - RATIO / 2: req_aux = AXIS_X_POS - pos_of_y if (req_aux != 0): print(pos_of_y * ' ' + '*' + (req_aux - 1) * ' ' + '|') else: print((AXIS_X_POS - 1) * ' ' + '*' + '|') elif y1_cur_value >= 0 + RATIO / 2: req_aux = pos_of_y - AXIS_X_POS if (req_aux != 0): print(AXIS_X_POS * ' ' + '|' + (req_aux - 1) * ' ' + '*') else: print((AXIS_X_POS) * ' ' + '|*') else: print(AXIS_X_POS * ' ' + '*') else: print('|' + pos_of_y* ' ' + '*') AXIS_X_POS = 0 from_x += pace_x print((dial_length + AXIS_X_POS) * ' ' + '|\n', (dial_length + AXIS_X_POS - 3) * ' ' + 'x V') 

Bagian kode ini bertanggung jawab langsung untuk mencetak grafik itu sendiri.

 print("{1:^{0}.6g}".format(dial_length, from_x), end='') 

Di sini, formatnya sangat berguna dan menyederhanakan kode. ^ memungkinkan kita untuk menyelaraskan angka di tengah area yang dipilih (dalam hal ini, 12 posisi). g bertanggung jawab atas angka - jika mereka tidak memiliki bagian pecahan, maka tidak akan dicetak (angka sebagai int), jika tidak - 6 tempat desimal

Karena grafik kita terbatas pada spasi 80 karakter di sepanjang sumbu y, pada grafik kita nilai fungsi pada titik tersebut akan bertepatan dengan sumbu x tidak hanya dalam kasus y1 (x) = 0, tetapi juga di sekitarnya [0 - RATIO / 2, 0 + RATIO / 2].

Secara total, kami memiliki tiga kasus lokasi tanda bintang (yaitu, titik) dan tongkat vertikal (yaitu, sumbu x): '* |' (y1 (x) <= 0 - RATIO / 2), '*' (0 - RATIO / 2 <y1 (x) <0 + RATIO / 2), '| *' (y1 (x)> = 0 + RATIO / 2), kami akan mempertimbangkan tiga kasus ini.

1. y1 (x) <= 0 - RATIO / 2
   Dalam hal ini, titik tersebut terletak pada sumbu x, jadi kami mencari jarak dari titik ke sumbu dalam spasi. Karena pembulatan angka, mungkin terjadi bahwa nilai-nilai variabel AXIS_X_POS dan pos_of_y mungkin bertepatan. Tetapi ini tidak mungkin, karena dalam kasus ini kita akan berada dalam kasus ketiga. Dalam kasus kami, titik tidak sesuai dengan sumbu x, oleh karena itu diperlukan kondisi tambahan, yang akan mengurangi 1 variabel pos_of_y dalam kasus kesetaraan.
2. y (x)> = 0 + RASIO / 2
   Kasing identik dengan kasing pertama, hanya titik yang akan terletak di sisi lain dari sumbu x dan semua tindakan di atas disesuaikan untuk ini
3. sisanya
   Kasing paling sederhana - cukup cetak tanda bintang di tempat aksis

Itu jika kita memiliki nilai negatif (y1 (x) <0). Jika tidak, ketikkan saja '|' dan menentukan posisi titik.

Baiklah, kita akhiri program dengan sumbu x tambahan.

Jadi, kode yang berakhir:

 dial_length = 12 label = "  y1 = x**3 - 2*x**2 + 4*x - 8" print("{1:^{0}.6f}".format(dial_length, x_copy)) print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 81, 'y' , 82*'-']), end=''); MAX_Y1_VALUE_DIFFERENCE = (max_y1_value - min_y1_value) + \ (max_y1_value == min_y1_value) RATIO = MAX_Y1_VALUE_DIFFERENCE / 80 AXIS_X_POS = abs(int((- min_y1_value) / RATIO)) if (AXIS_X_POS > 80): AXIS_X_POS = 81 while (is_sequence_decreasing and from_x >= to_x) or \ (not is_sequence_decreasing and from_x <= to_x): y1_cur_value = y1(from_x) cur_y1_value_and_min_difference = (y1_cur_value - min_y1_value) + \ (y1_cur_value == min_y1_value) * \ ((max_y1_value == min_y1_value)) pos_of_y = int(cur_y1_value_and_min_difference * 80 / \ MAX_Y1_VALUE_DIFFERENCE) print("{1:^{0}.6g}".format(dial_length, from_x), end='') if (negative_value_exists): if y1_cur_value <= 0 - RATIO / 2: req_aux = AXIS_X_POS - pos_of_y if (req_aux != 0): print(pos_of_y * ' ' + '*' + (req_aux - 1) * ' ' + '|') else: print((AXIS_X_POS - 1) * ' ' + '*' + '|') elif y1_cur_value >= 0 + RATIO / 2: req_aux = pos_of_y - AXIS_X_POS if (req_aux != 0): print(AXIS_X_POS * ' ' + '|' + (req_aux - 1) * ' ' + '*') else: print((AXIS_X_POS) * ' ' + '|*') else: print(AXIS_X_POS * ' ' + '*') else: print('|' + pos_of_y* ' ' + '*') AXIS_X_POS = 0 from_x += pace_x print((dial_length + AXIS_X_POS) * ' ' + '|\n', (dial_length + AXIS_X_POS - 3) * ' ' + 'x V') 

Jalankan program pada beberapa tes






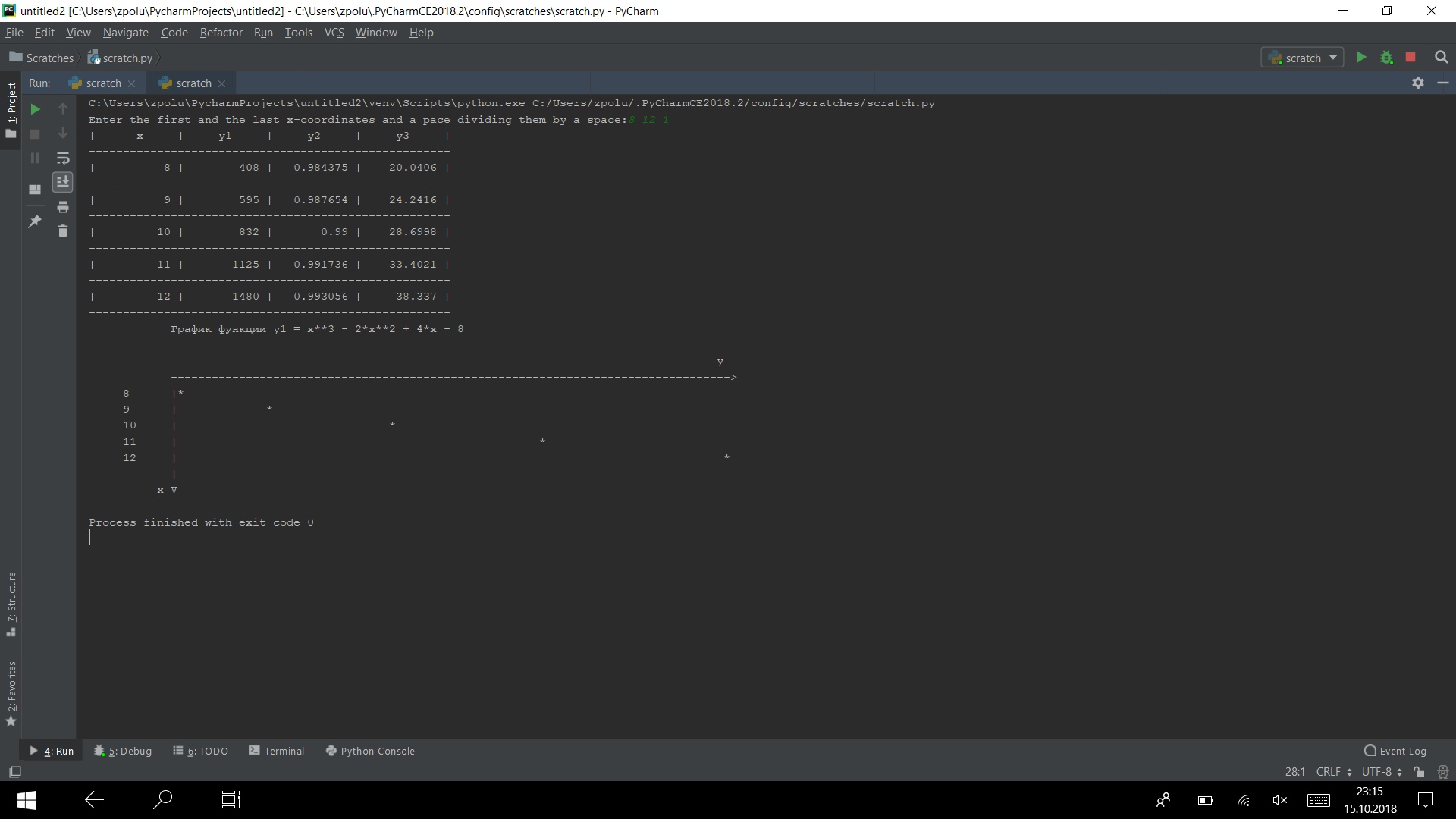
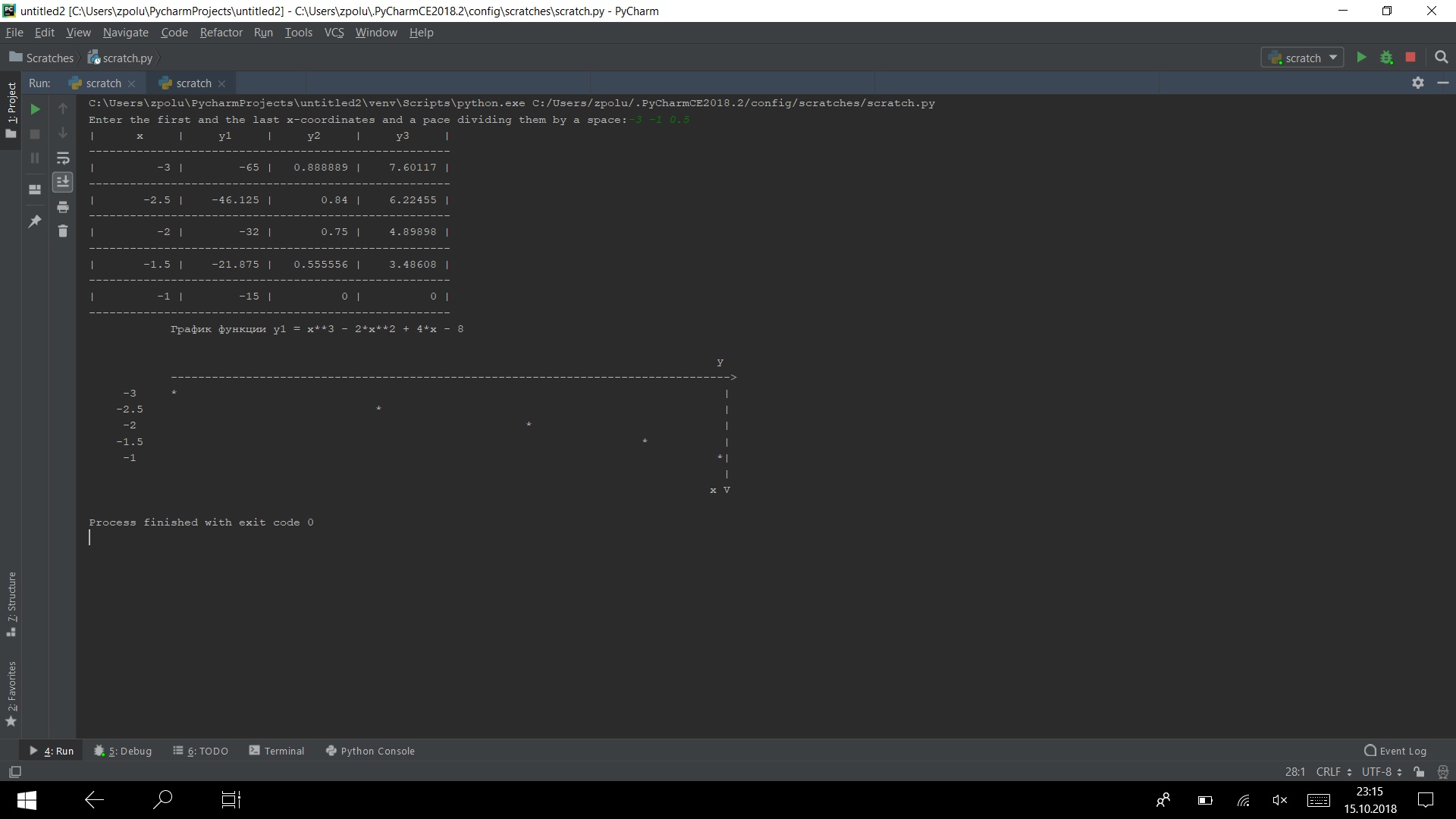
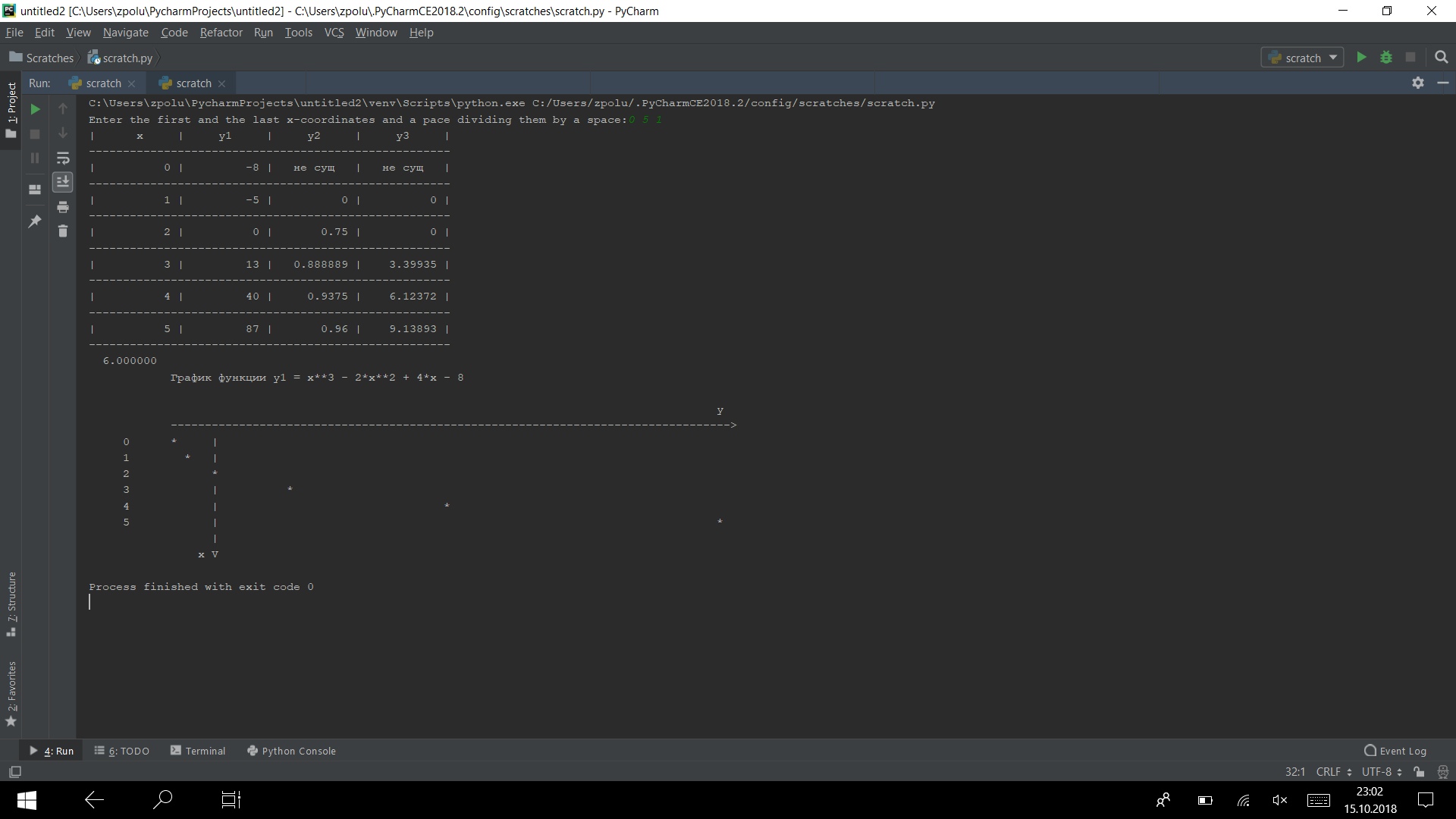
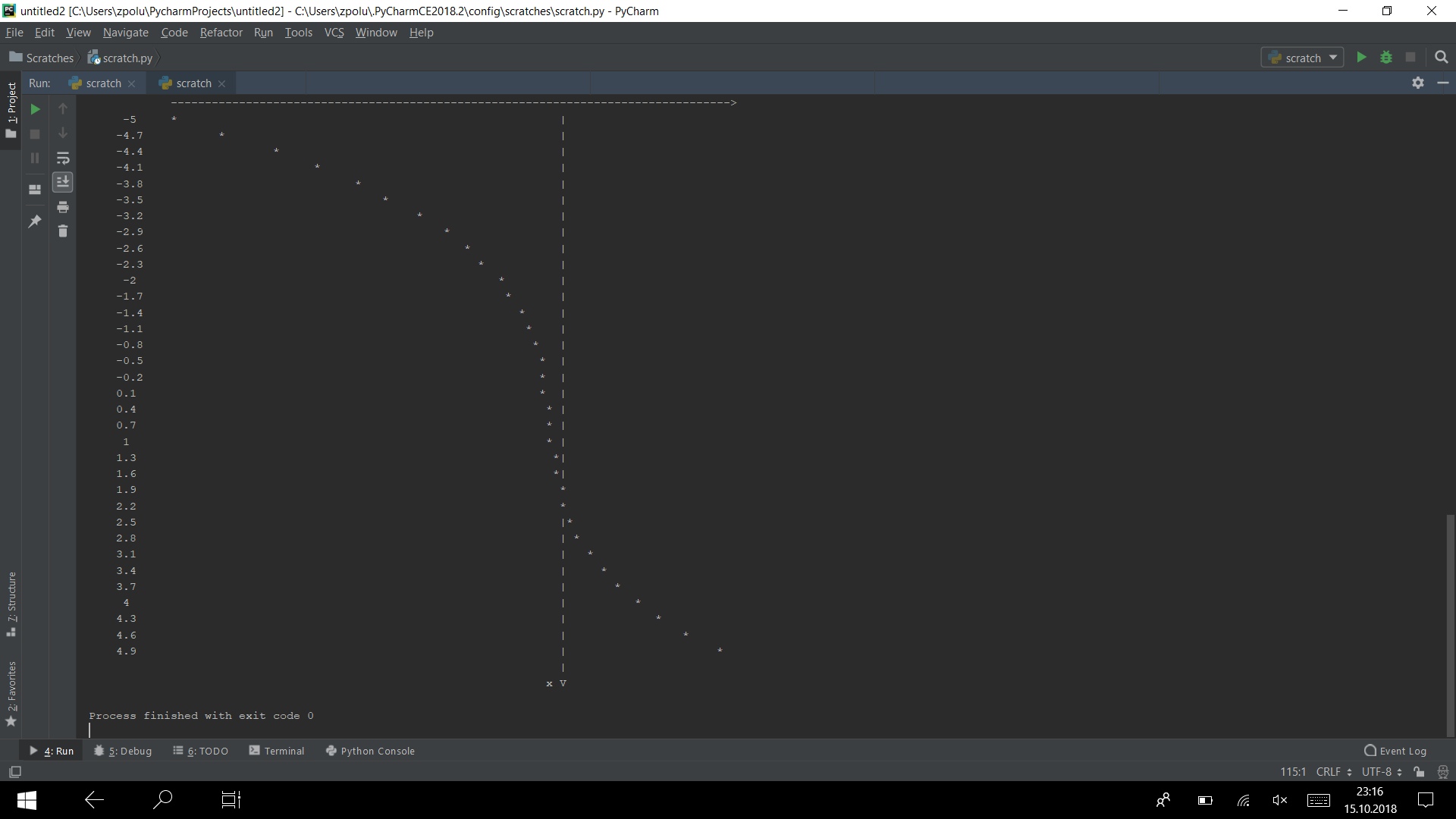
Ini bekerja)