Spiral berputar: matematika dan halusinasi

Ketika mencoba membayangkan halusinasi yang disebabkan oleh zat narkotika, berputar-putar, bentuk-bentuk spiral psychedelic segera menyerupai penglihatan terowongan datang ke pikiran. Tetapi struktur geometris seperti itu dapat menyebabkan tidak hanya obat-obatan halusinogen seperti LSD, kanabis atau mescaline . Orang-orang berbicara tentang terjadinya penglihatan seperti itu pada saat mereka berada di kematian, selama kondisi yang menyakitkan seperti epilepsi dan skizofrenia, sebagai akibat dari kekurangan sensorik , atau bahkan setelah tekanan sederhana pada bola mata. Halusinasi geometris sedemikian luasnya sehingga selama abad terakhir, para ilmuwan mulai bertanya-tanya apakah mereka dapat memberi tahu kita sesuatu yang mendasar tentang struktur otak kita. Dan, rupanya begitu.


Bentuk konstanta yang dibuat di komputer. Dua gambar teratas meniru corong dan spiral yang terjadi setelah menerima LSD. Kiri bawah adalah sarang madu yang dibuat oleh ganja. Kanan bawah adalah web.

Halusinasi geometris sistematis pertama kali mulai diselidiki pada 1920-an oleh seorang psikolog Amerika-Jerman, Heinrich Kluver . Ketertarikan Kluver pada persepsi visual akhirnya membuatnya bereksperimen dengan peyote , kaktus, dirayakan oleh Carlos Castaneda , yang bahan psikoaktifnya, mescaline, memainkan peran penting dalam ritual perdukunan dari banyak suku Amerika Tengah. Mescaline terkenal karena menyebabkan halusinasi visual yang jelas. Menggunakan peyote di laboratorium dengan asisten, Kluver memperhatikan pengulangan bentuk geometris dalam halusinasi yang disebabkan oleh mescaline, dan membaginya menjadi empat jenis, menyebutnya sebagai konstanta : terowongan dan corong, spiral, kisi, yang meliputi sarang lebah dan segitiga, dan sarang laba-laba.

Pada 1970-an, ahli matematika Jack Cowan dan Bard Ermentraut menggunakan klasifikasi Kluver untuk membuat teori yang menggambarkan apa yang terjadi di otak ketika itu membuat kita percaya bahwa kita melihat pola geometris. Teori mereka dikembangkan lebih lanjut oleh ilmuwan lain, termasuk Paul Breslov, seorang profesor matematika dan neurobiologi komputasi di Oxford Center for Collaborative Applied Mathematics.

Di mana potongan-potongan dari korteks serebral *

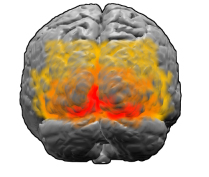Korteks visual. Area bertanda merah V1

[ * Rujukan ke dongeng Vietnam "Di mana harimau berasal dari strip" / sekitar. perev. ]

Area pertama korteks visual otak yang memproses gambar pada manusia dan mamalia adalah area yang dikenal sebagai V1. Bukti eksperimental, seperti gambar fMRI , menunjukkan bahwa pola Kluver juga sebagian besar berasal dari V1, dan tidak muncul kemudian di suatu tempat dalam sistem visual. Seperti bagian otak lainnya, V1 memiliki struktur yang kompleks, berkerut, terlipat - namun, ada cara yang sangat mudah untuk menerjemahkan apa yang kita lihat di bidang penglihatan kita ke dalam aktivitas neuron di V1. "Bayangkan kita sedang menyebarkan V1," kata Breslov. - Dapat dibayangkan sebagai jaringan saraf setebal beberapa milimeter, dengan berbagai lapisan neuron. Dalam perkiraan pertama, neuron sepanjang kedalaman korteks berperilaku serupa, jadi jika Anda meratakannya, Anda dapat membayangkan V1 sebagai lembaran dua dimensi. "

Objek atau pemandangan dunia visual diproyeksikan dalam bentuk gambar dua dimensi ke retina setiap mata, sehingga apa yang kita lihat juga dapat dianggap sebagai lembaran datar: bidang pandang. Setiap titik pada lembar ini dapat ditunjuk oleh dua koordinat, seperti titik pada peta, atau titik pada model datar V1. Area terang dan gelap yang berselang-seling yang membentuk halusinasi geometris disebabkan oleh area bergantian aktivitas neuron tinggi dan rendah di V1 - area di mana neuron diaktifkan dengan sangat cepat, dan area di mana kebalikannya benar.

Untuk menerjemahkan pola visual ke dalam aktivitas neuron, kisi-kisi koordinat diperlukan - suatu aturan yang dengannya setiap titik bidang pandang dihubungkan dengan titik model pesawat V1. Pada 1970-an, para ilmuwan, termasuk Cowen, membuat kisi-kisi semacam itu berdasarkan pengetahuan anatomi interaksi neuron retina dengan neuron di V1. Untuk setiap bagian terang atau gelap dari bidang pandang, pemetaan mendefinisikan sebagian aktivitas neuron tinggi atau rendah di V1.

Bagaimana pencitraan retina dan korteks ini mengubah pola geometri Kluver? Ternyata halusinasi, yang menyebabkan spiral, lingkaran, dan sinar yang berasal dari pusat, berhubungan dengan strip aktivitas neuron dalam V1 yang lewat pada sudut tertentu. Kisi-kisi seperti sarang lebah atau sel berhubungan dengan pola aktivitas heksagonal di V1. Ini sendiri mungkin tidak begitu menarik, tetapi ada satu preseden: itu adalah garis-garis dan segi enam yang diamati oleh para ilmuwan ketika memodelkan contoh-contoh lain dari pembentukan pola, misalnya, konveksi cairan, atau, yang lebih mengejutkan, munculnya bintik-bintik dan garis-garis pada kulit binatang. Matematika yang mengatur pembentukan pola-pola ini sudah dikenal luas, dan juga mengusulkan mekanisme untuk memodelkan fungsi korteks visual.

Dari bidang pandang ke korteks visual

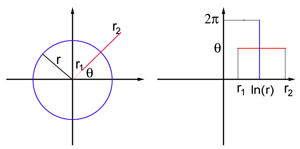
Bayangkan bidang pandang dalam bentuk lembaran datar dengan koordinat kutub: setiap titik P didefinisikan oleh dua angka, (r, θ), di mana r adalah jarak ke titik asal, dan θ adalah sudut antara segmen OP dan sumbu x. Titik referensi sesuai dengan pusat bidang tampilan. V1 juga dimodelkan sebagai lembaran datar, tetapi kali ini memiliki koordinat Cartesian (x, y). Tampilan koordinat yang tepat dari bidang tampilan dan model bidang V1 terlalu rumit untuk artikel ini, tetapi untuk poin yang cukup jauh dari pusat bidang tampilan (yaitu, untuk r yang cukup besar) itu menyerupai peta logaritmik:

$$

$$x = \ ln {r} \\ y = \ theta$$

Pemetaan menerjemahkan lingkaran jari-jari r dalam bidang pandang menjadi segmen vertikal lurus dengan x = ln r, dan sinar yang berasal dari asal koordinat O pada sudut θ ke dalam segmen horizontal lurus dengan y = θ

Di mana tempat macan tutul

Model pertama untuk membentuk pola kulit binatang berasal dari Alan Turing , yang lebih dikenal sebagai bapak ilmu komputer modern dan seorang hacker dari Bletchley Park yang memecahkan kode. Turing tertarik pada bagaimana sistem spasial yang homogen seperti bola sel yang seragam, yang merupakan embrio hewan, dapat membuat pola spasial yang tidak homogen, tetapi statis, seperti garis-garis zebra.

Turing menyarankan bahwa pola-pola ini muncul sebagai hasil dari proses difusi reaksi . Bayangkan embrio hewan yang kulitnya dua senyawa kimia hidup. Salah satunya adalah inhibitor yang menekan produksi baik itu sendiri maupun bahan kimia lainnya. Yang lainnya adalah katalis yang menyebabkan produksi kedua zat.

Pada saat awal model Turing, dua bahan kimia idealnya saling menyeimbangkan - mereka berada dalam kesetimbangan, dan konsentrasi mereka pada titik yang berbeda pada embrio tidak berubah seiring waktu. Sekarang bayangkan bahwa untuk beberapa alasan, pada satu titik, konsentrasi katalis sedikit meningkat. Gangguan kecil ini membuat seluruh sistem bergerak. Peningkatan konsentrasi lokal dari katalis berarti bahwa lebih banyak katalis dan inhibitor diproduksi di sana. Namun, kedua senyawa juga berdifusi pada kulit embrio, menghambat dan mengkatalisasi produksi mereka di tempat lain.

Misalnya, jika inhibitor berdifusi lebih cepat dari katalis, ia akan dengan cepat mengelilingi titik gangguan dan mengurangi konsentrasi katalis di dalamnya. Sebagai hasilnya, kami mendapatkan bagian dengan katalis konsentrasi tinggi, dikelilingi oleh inhibitor konsentrasi tinggi - dengan kata lain, titik katalis pada latar belakang inhibitor. Tergantung pada tingkat difusi dari dua senyawa, ada kemungkinan bahwa pola yang terlihat seperti itu muncul di seluruh kulit embrio, dan akhirnya stabil.

Thuring menuliskan sistem persamaan diferensial yang menggambarkan persaingan antara dua senyawa - Anda dapat membiarkannya berkembang dalam waktu dan melihat apakah pola muncul. Persamaan ini bergantung pada parameter yang menggambarkan laju difusi dua senyawa: jika Anda memilihnya dengan benar, sistem akhirnya akan stabil, membentuk pola tertentu yang dapat diubah dengan mengubah parameter. Tautan menyediakan applet di Jawa , di mana Anda dapat bermain-main dengan parameter dan melihat pola yang dihasilkan.

Persamaan Pola Hewan

Untuk kesederhanaan, bayangkan embrio dalam bentuk garis satu dimensi. Kapan saja t dan pada setiap titik x embrio, konsentrasi katalis (aktivator) dan inhibitor (inhibitor) ditentukan oleh fungsi A (x, t) dan I (x, t). Mereka berubah seiring waktu sesuai dengan aturan berikut:

$$

$$\ frac {\ partial A} {\ partial t} = f (A, I) + \ frac {\ partial ^ 2 A} {\ partial x ^ 2} \\ \ frac {\ partial I} {\ partial t } = g (A, I) + d \ frac {\ partial ^ 2 I} {\ partial x ^ 2}$$

Istilah pertama di sebelah kanan setiap persamaan menggambarkan jumlah produksi katalis dan penghambat. Mereka adalah fungsi konsentrasi katalis dan inhibitor, karena keduanya mempengaruhi laju reaksi.

Istilah kedua di sebelah kanan setiap persamaan adalah turunan kedua, yang menggambarkan laju perubahan gradien katalis dan inhibitor. Mereka mengatur laju difusi.

Istilah tambahan d di sisi kanan persamaan kedua adalah koefisien difusi, yang menunjukkan seberapa besar inhibitor berdifusi lebih cepat daripada katalis. Turing telah menunjukkan bahwa keunggulan dalam kecepatan inhibitor adalah parameter penting untuk pembuatan noda.

Pola otak

Aktivitas neuron di otak bukanlah proses reaksi-difus, namun memiliki analogi dengan model Turing. "Neuron saling mengirim sinyal melalui saluran keluaran data yang disebut akson," kata Breslov. Neuron bereaksi terhadap sinyal satu sama lain, inilah reaksinya. "Sinyal bergerak sangat cepat dibandingkan dengan proses pola sehingga mereka dapat disalahartikan sebagai interaksi instan." Karena itu, alih-alih difusi, proses lokal, kami memiliki interaksi instan di kejauhan. Peran katalis dan inhibitor dimainkan oleh dua kelas neuron yang berbeda. “Ada neuron-neuron rangsang - yang meningkatkan kemungkinan neuron-neuron lain menjadi aktif - dan ada neuron-neuron penghambat yang mengurangi kemungkinan ini,” kata Breslov. "Persaingan antara dua kelas neuron analog dengan mekanisme katalis-inhibitor dalam model Turing."


Pola garis, heksagonal, dan persegi panjang dari aktivitas saraf pada V1 dihasilkan oleh model matematika

Terinspirasi oleh analogi proses Turing, Cowan dan Ermentraout menciptakan model aktivitas saraf di V1 menggunakan seperangkat persamaan yang dirumuskan oleh Cowan dan Hugh Wilson. Meskipun persamaan ternyata lebih rumit daripada Turing, Anda masih bisa memainkan permainan yang sama, membiarkan sistem berkembang dari waktu ke waktu dan melihat apakah pola aktivitas saraf berkembang. "Anda dapat menemukan bahwa dalam kondisi tertentu, jika Anda meningkatkan parameter, mewakili, misalnya, efek obat pada korteks, ini akan mengarah pada pertumbuhan pola periodik," kata Breslov.

Model Cowan dan Ermentraut menunjukkan bahwa halusinasi geometris dihasilkan dari ketidakstabilan di V1: sesuatu, misalnya, keberadaan obat, menghilangkan jaringan saraf dari keadaan seimbang, memulai proses interaksi pertumbuhan bola salju antara neuron yang menarik dan menekan, yang kemudian menstabilkan. dalam bentuk pola bergaris atau heksagonal aktivitas saraf di V1. Kemudian kita "mengamati" pola ini dalam bentuk struktur geometris yang dijelaskan oleh Kluver di bidang pandang.

Simetri di otak

Faktanya, semuanya tidak sesederhana dalam model Cowan dan Ermentraut, karena neuron merespons tidak hanya pada gambar terang dan gelap. Dengan ketebalan V1, neuron berbaris dalam kolom yang dikenal sebagai hypercolumns , yang masing-masing kira-kira merespons sebagian kecil dari bidang visual. Tetapi tidak semua neuron dalam hypercolumn adalah sama: selain mengenali area terang dan gelap, setiap neuron berspesialisasi dalam mengenali wajah lokal - garis yang memisahkan area terang dan gelap dalam satu bagian gambar - orientasi tertentu. Beberapa mengenali wajah horisontal, yang lain - vertikal, yang lain - wajah yang terletak pada sudut 45 °, dan seterusnya. Setiap hypercolumn berisi kolom neuron dari semua orientasi yang disukai, oleh karena itu, hypercolumn dapat menanggapi wajah semua orientasi di area tertentu dari bidang visual. Ini adalah komposisi hypercolumns dan preferensi orientasi yang memungkinkan kita mengenali kontur, permukaan, dan tekstur dunia visual.


Koneksi di V1: Neuron dalam hypercolumn berinteraksi dengan sebagian besar neuron lainnya. Tetapi mereka bereaksi dengan neuron dalam hypercolumns lain hanya jika kolom berada di arah orientasi mereka, dan neuron memiliki preferensi orientasi yang sama.

Dalam beberapa tahun terakhir, cukup banyak bukti anatomi yang telah dikumpulkan tentang bagaimana neuron berinteraksi satu sama lain dengan preferensi orientasi yang berbeda. Di dalam geo-kolom mereka, neuron berinteraksi dengan sebagian besar neuron lain, terlepas dari preferensi mereka. Tetapi, untuk neuron-hyperon kolom lainnya, mereka bertindak lebih selektif, hanya berinteraksi dengan neuron-neuron dengan preferensi yang serupa, sehingga dapat menjamin kita kemampuan untuk mengenali kontur kontinu dalam dunia visual.

Breslov, bersama-sama dengan Cowan, ahli matematika Martin Golubitsky dan ilmuwan lainnya, menggeneralisasi model asli Cowen dan Ermentraut untuk memperhitungkan bukti anatomi baru ini. Mereka kembali menggunakan pesawat sebagai dasar model V1: setiap hypercolumn diwakili di pesawat dengan titik (x, y), dan setiap titik (x, y) sesuai dengan hypercolumn. Neuron dengan preferensi yang diberikan untuk orientasi θ (di mana θ adalah sudut antara 0 dan π ditunjukkan oleh posisi hypercolumn (x, y) bersama dengan sudut θ - yaitu, mereka ditunjukkan oleh tiga unit informasi, (x, y, θ). Model V1 bukan pesawat, tetapi pesawat dengan set orientasi penuh untuk setiap titik.


Jika dua elemen, (x, y, θ) dan (s, t, θ) berinteraksi, maka elemen lain dengan orientasi yang sama berinteraksi pada titik (x + a, y + b) dan (s + a, t + b ), dan elemen dengan orientasi -θ pada titik (x, -y) dan (s, -t).

Untuk mematuhi bukti anatomi, Breslov dan rekannya menyarankan bahwa neuron yang ditunjukkan oleh titik (x ₀ , y ₀ , θ ₀ ) berinteraksi dengan semua neuron lain dalam hypercolumn yang sama (x ₀ , y ₀ ). Tapi dia berinteraksi dengan neuron dari hypercolumns lain hanya jika mereka terletak pada orientasi pilihannya θ ₀ : di pesawat, Anda perlu menggambar garis melalui titik (x ₀ , y ₀ ) pada sudut θ ₀ . Kemudian neuron yang dilambangkan dengan titik (x ₀ , y ₀ , θ ₀ ) berinteraksi hanya dengan neuron hypercolumns yang terletak pada garis yang sama, yaitu, memiliki orientasi pilihan yang sama θ ₀ .

Skema interaksi ini sangat simetris. Misalnya, itu tidak berubah ketika pesawat bergeser ke arah mana pun dengan jarak apa pun: jika dua elemen, (x ₀ , y ₀ , θ ₀ ) dan (s ₀ , t ₀ , φ ₀ ), berinteraksi, maka elemen-elemen yang diperoleh oleh shift, (x ₀ + a, y ₀ + b, θ ₀ ) dan (s ₀ + a, t ₀ + b, φ ₀ ) untuk beberapa a dan b, berinteraksi dengan cara yang sama. Dengan prinsip yang sama, skema ini tidak berubah dalam hal rotasi dan refleksi pesawat.


Halusinasi kisi yang diciptakan oleh model matematika. Ini sangat menyerupai halusinasi yang terjadi ketika mengambil ganja.

Breslov dan rekannya menggunakan versi umum persamaan dari model asli untuk memungkinkan sistem untuk berkembang. Hasilnya adalah model yang tidak hanya lebih akurat dalam hal anatomi V1, tetapi juga mampu menghasilkan pola-pola geometris di bidang pandang bahwa model asli tidak mampu. Ini termasuk terowongan kisi, sarang lebah dan sarang laba-laba, orientasi kontur yang mencirikan mereka lebih baik daripada daerah kontras terang dan gelap.

Selain itu, model ini peka terhadap simetri skema interaksi neuron: matematikawan telah menunjukkan bahwa simetri inilah yang menghasilkan pembentukan pola periodik aktivitas saraf. Oleh karena itu, model ini mengasumsikan bahwa halusinasi menimbulkan pengaturan hypercolumns dan preferensi orientasi, yaitu, mekanisme yang membantu kita mengenali wajah, kontur, permukaan dan tekstur dunia visual. Ketika mekanisme ini kehilangan stabilitas, misalnya, sebagai akibat dari paparan obat, pola aktivitas muncul yang berubah menjadi halusinasi visual.

Di luar halusinasi

Model Breslov tidak hanya memungkinkan seseorang untuk mendapatkan wawasan tentang mekanisme yang menghasilkan halusinasi visual, tetapi juga memberikan petunjuk tentang arsitektur otak dalam arti yang lebih luas. Bersama dengan istrinya, seorang ahli neurobiologi eksperimental, Breslov mempelajari kontur koneksi hypercolumn dengan penglihatan normal untuk memahami bagaimana gambar visual diproses. “Orang-orang terbiasa percaya bahwa neuron dalam V1 hanya mengidentifikasi wajah-wajah lokal, dan bahwa seseorang perlu pergi ke tingkat otak yang lebih tinggi untuk mengumpulkan wajah-wajah ini dan mengenali hal-hal yang lebih kompleks seperti kontur dan permukaan. Tetapi dari pekerjaan kami dengan istri saya, jelas bahwa struktur-struktur di V1 ini benar-benar memungkinkan korteks visual untuk mengenali kontur pada tahap awal dan melakukan pemrosesan yang lebih global. Dipercayai bahwa kita memproses aspek gambar yang semakin kompleks, naik lebih tinggi dalam hierarki otak. Sekarang menjadi jelas bahwa ada umpan balik aktif antara bagian atas dan bawah dari korteks."Ini bukan proses hierarkis sederhana, tetapi sistem yang sangat kompleks dan aktif, yang akan membutuhkan waktu bertahun-tahun untuk memahami."

Di antara aplikasi praktis dari pekerjaan ini adalah visi komputer - ilmuwan komputer sudah membangun struktur dengan koneksi internal yang dimainkan oleh Breslov dan rekannya untuk membangun model untuk mengajarkan komputer bagaimana mendefinisikan kontur dan tekstur. Jika Anda menunjukkan sedikit imajinasi, Anda dapat membayangkan bahwa studi ini suatu hari nanti akan dapat membantu mengembalikan visi kepada para penyandang cacat. "Pertanyaannya adalah apakah mungkin untuk merangsang bagian dari korteks visual, memotong mata, dan menggunakannya untuk mengarahkan orang buta," kata Breslov. "Jika Anda memahami bagaimana korteks terstruktur dan bagaimana reaksinya terhadap stimulasi, mungkin kemudian akan mungkin untuk menemukan metode terbaik untuk stimulasi yang benar."

Bahkan ada area aplikasi yang sama sekali tidak terhubung dengan otak. Breslov menerapkan ide-ide yang diperoleh melalui karyanya ke situasi lain di mana benda-benda terletak di ruang dengan orientasi tertentu, misalnya, fibroblast dari jaringan manusia dan hewan. Dia menunjukkan bahwa dalam kondisi tertentu, sel dan molekul yang berinteraksi ini dapat berbaris dan menghasilkan pola yang mirip dengan yang muncul pada V1.

Orang-orang berbicara tentang melihat halusinasi sejak awal waktu, dan di hampir semua budaya - gambar halusinasi bahkan dapat ditemukan dalam petroglyphsdan lukisan gua. Dalam tradisi dukun di seluruh dunia mereka diperlakukan sebagai pesan dari dunia roh. Beberapa ahli ilmu saraf modern akan setuju dengan keterlibatan roh dalam hal ini, tetapi sebagai pembawa pesan dari dunia tersembunyi - kali ini, dunia otak kita yang tersembunyi - halusinasi ini tidak kehilangan potensi mereka.