Neurotic Bikes: Genesis

Suatu hari, Youtube berpikir bahwa saya akan merasa menarik untuk menonton video berjudul "AI Belajar bermain Hill Climb Racing." Lucu sekali, karena beberapa menit sebelumnya saya telah melakukan perubahan berikutnya pada proyek, di mana kolega saya dan saya, di sela-sela pekerjaan dan kerja, menyelesaikan masalah ini. Benar, tidak ada "AI" dalam video itu - penulis menghibur penonton dengan mengumbar Box2D dan menenangkannya. Namun demikian, saya mengusulkan untuk mempertimbangkan fakta ini sebagai bukti yang meyakinkan tentang relevansi topik dan membongkar perangkat mainan kami.

Secara singkat tentang tugas: kendaraan - dalam kasus kami adalah Alien, atau mesin jahit Singer di atas roda, sebut saja "agen" - harus berkendara di sepanjang bukit pasir dengan kebisingan nama yang sama dari awal hingga selesai. Seperti inilah bentuk agen di kotak pasirnya:



Seorang agen yang menyentuh bagian belakang trek atau tidak menunjukkan semangat yang tepat dalam bergerak menuju tujuan dihapus dari trek.

Kami akan memecahkan masalah menggunakan jaringan saraf, tetapi dioptimalkan oleh algoritma genetika (GA) - proses semacam itu disebut neuroevolution . Kami menggunakan metode NEAT (NeuroEvolution of Augmenting Topologies) yang ditemukan oleh Kenneth Stanley dan Risto Miikkulainen pada awal abad ini [1] : pertama, ia bekerja dengan baik dalam masalah - masalah penting bagi perekonomian nasional, dan kedua, kami mulai mengerjakan proyek tersebut sudah memiliki kerangka kerja sendiri menerapkan NEAT. Jadi, terus terang, kami tidak memilih metode solusi - melainkan, kami memilih tugas di mana Anda dapat mengarahkan apa yang sudah siap.

Gambar tersebut menunjukkan skema perkiraan algoritma genetika:



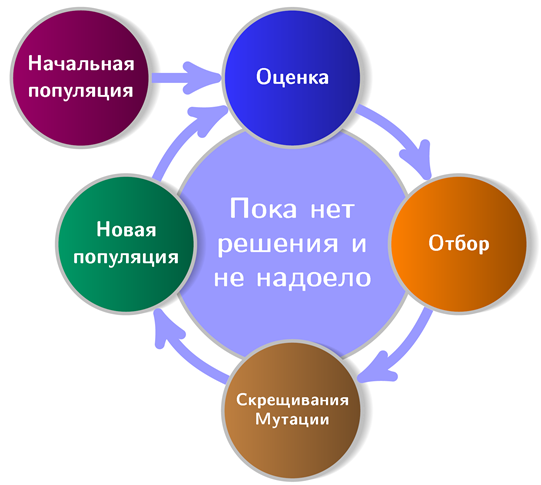
Dapat dilihat bahwa GA yang layak dimulai dari populasi awal ( populasi adalah sekumpulan solusi potensial). Kami akan terlibat dalam penciptaannya dan pada saat yang sama berkenalan dengan prinsip pertama NEAT . Menurut prinsip ini, semua agen dalam populasi awal harus memiliki topologi jaringan saraf "minimal" yang paling sederhana. Apa hubungan topologi dengan itu? Faktanya adalah bahwa dalam NEAT bersama dengan optimasi bobot koneksi, arsitektur jaringan juga berkembang. Omong-omong, ini menghilangkan kebutuhan akan desainnya untuk tugas itu. Beralih dari arsitektur sederhana ke kompleks tidak hanya logis, tetapi juga praktis (ada lebih sedikit ruang pencarian), jadi Anda harus mulai dengan topologi minimum yang mungkin - ini adalah alasan penulis metode ini beralasan.

Untuk kasus kami dan semua kasus serupa, topologi minimal ini berasal dari pertimbangan berikut. Untuk melakukan sesuatu yang berarti, agen perlu:

• memiliki informasi tentang lingkungan dan kondisinya,
• memproses informasi ini
• berinteraksi dengan duniamu.

Peran pertama dimainkan oleh sensor - neuron pada lapisan input, yang akan kami berikan informasi yang berguna bagi agen. Neuron lapisan keluaran akan memproses data dari sensor. Aktor - perangkat yang melakukan tindakan mekanis sebagai respons terhadap sinyal dari neuron "mereka" pada lapisan keluaran - bertanggung jawab untuk berinteraksi dengan lingkungan. Dengan demikian, prinsip umum membangun konfigurasi awal adalah sebagai berikut: kami menentukan dengan sensor dan aktuator, mulai satu neuron per aktuator, kami menghubungkan semua sensor dan satu lagi neuron khusus - neuron perpindahan ( bias , tentang hal itu di bawah) dengan bobot acak ke semua neuron lapisan output. Sesuatu seperti ini:



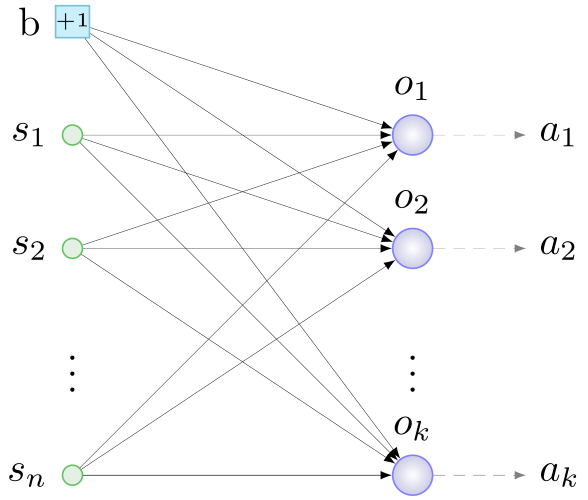b - bias, s - sensor, o - neuron pada lapisan keluaran, a - aktuator, n - jumlah sensor, k - jumlah aktuator

Dan di sini adalah NS minimum untuk tugas kami:



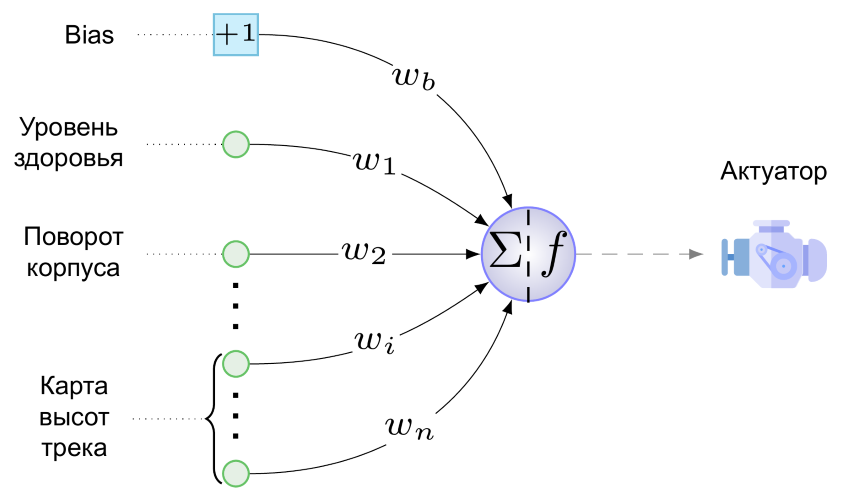
Kami hanya memiliki satu aktuator - ini adalah mesin kreasi beroda kami. Belum tahu cara menembak, melompat dan memainkan pipa. Nilai berikut dipasok ke mesin dari neuron tunggal pada lapisan keluaran (sayang rasanya menyebutnya lapisan):


Di sini wb adalah nilai bobot koneksi yang bergerak dari bias ke neuron output, dikalikan dengan fakta bahwa bias apa pun "menghasilkan", yaitu. +1, s _i adalah nilai yang dinormalisasi ke kisaran [0,1] pada sensor ke-i, w _i adalah nilai bobot koneksi dari sensor ke-ke sensor neuron keluaran, dan f adalah fungsi aktivasi.

Sebagai fungsi aktivasi, kami menggunakan fantasi softsign ini:


- Dia mendemonstrasikan kinerja terbaik dalam tes seorang neuro-evolusionis terkenal di kalangan sempit [2] . Dan tidak masuk akal untuk membandingkan kelembutan tikungan dan simetri grafik fungsi ini dengan Leaky ReLU yang bengkok dengan sudut:



Gambar ini menunjukkan reaksi agen terhadap nilai yang berbeda dari fungsi aktivasi. Pada nilai yang mendekati satu, mesin memutar roda searah jarum jam, mempercepat agen ke depan dan memiringkan housing dengan kuat ke belakang, sehingga orang yang lemah, tetapi berani, dengan cepat membalikkan punggung dan mati. Dengan nilai mendekati 0, kebalikannya benar, dan dengan nilai 0,5, motor agen tidak bekerja.

Gambar yang sama menunjukkan peran neuron bias - bobot ikatan yang berpindah dari neuron ke neuron pada lapisan output bertanggung jawab, sebagai berikut dari (1), untuk besarnya dan arah bias f (x) di sepanjang abscissa. Garis putus-putus pada gambar menunjukkan grafik fungsi aktivasi pada w _b = -1. Ternyata bahkan tanpa adanya sinyal pada sensor, agen dengan koneksi semacam itu akan dengan cepat kembali: f (x) = f (-1 + 0) ≈0.083 <0,5. Secara umum, menggeser nilai fungsi secara horizontal memungkinkan penyimpangan koneksi secara halus (baik atau tebal, tergantung pada bobot) menyesuaikan reaksi mesin terhadap semua nilai sensor dan bobot koneksi mereka sekaligus. Tampaknya dimensi baru telah ditambahkan ke ruang pencarian (nilai "benar" untuk wb harus ditemukan), tetapi manfaat dalam bentuk tingkat kebebasan tambahan lebih besar daripada kemungkinan perpindahan seperti itu.

Yah, kami mempresentasikan jaringan saraf agen dari populasi awal masa depan. Tetapi NEAT adalah algoritma genetika, dan ia bekerja dengan genotipe - struktur dari mana jaringan terbentuk atau, lebih umum, fenotipe dalam proses penguraian kode. Karena kami mulai dengan fenotip, kami akan melakukan semuanya mundur: mencoba menyandikan jaringan yang disajikan di atas dalam genotipe. Di sini Anda tidak dapat melakukannya tanpa prinsip NEAT kedua , esensi utamanya adalah sebagai berikut: dalam genotipe, di samping struktur jaringan saraf dan bobot koneksinya, informasi disimpan pada sejarah asal-usul semua elemennya. Dengan pengecualian dari aspek historis ini, fenotip dikodekan dalam genotipe hampir "satu lawan satu", oleh karena itu, kami akan menggambarkan prinsip kedua dengan potongan-potongan jaringan saraf.

Nilai dari prinsip ini sulit untuk ditaksir terlalu tinggi - ini memberi agen kemungkinan reproduksi seksual. Topiknya agak rumit, jadi pertama-tama kita akan mempertimbangkan reproduksi aseksual . Itu terjadi seperti ini: salinan semua gen agen dibuat, salah satu dari beberapa jenis perubahan dibuat atas mereka - mutasi . Dalam versi NEAT kami, mutasi berikut dimungkinkan:

• perubahan berat koneksi
• batalkan tautan
• tambahkan tautan
• insersi neuron.

Tiga jenis mutasi pertama adalah sederhana dan dapat dimengerti tanpa penjelasan lebih lanjut. Penyisipan neuron ditunjukkan pada gambar di bawah, selalu terjadi di tempat koneksi yang ada, koneksi dihapus, dan dua yang baru muncul di tempatnya:



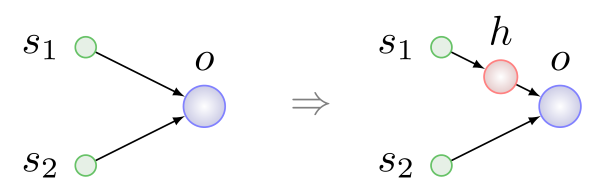
Di sini h adalah neuron tersembunyi .

Dua agen terlibat dalam reproduksi seksual atau kawin silang - orang tua, dan akibatnya sepertiga muncul - seorang anak. Dalam proses pembentukan genotipe anak, terjadi pertukaran, katakanlah, gen atau kelompok gen orang tua yang memiliki makna yang identik. Prinsip kedua adalah apa yang Anda butuhkan untuk mencari gen dengan makna yang sama.

Bayangkan kita ingin melakukan lintas agen dengan genotipe yang telah mengalami serangkaian mutasi berbeda dari daftar di atas:



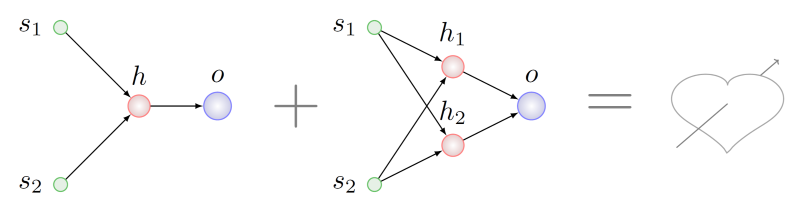
Tampaknya logis untuk mencari beberapa fragmen yang umum dalam hal topologi pada kedua orang tua dan mengambil sepotong fragmen ini untuk genotipe anak yang belum lahir. Akan sulit untuk melakukan ini, bahkan NP sulit dalam kasus umum, tetapi anggaplah kita berhasil. Dalam hal ini, kami menemukan bahwa di induk di sebelah kanan ada dua subgraf isomorfik ke grafik induk kiri. Pada gambar di bawah ini, busur dari subgraf ini disorot dalam berbagai warna:



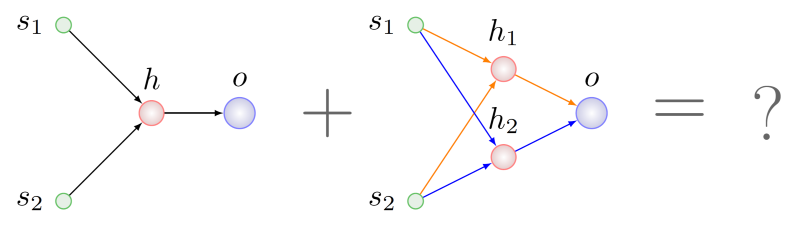
Yang mana yang akan dipilih untuk rekombinasi dengan gen induk kiri?

Mari kita beralih ke sejarah kemunculan genotipe ini:



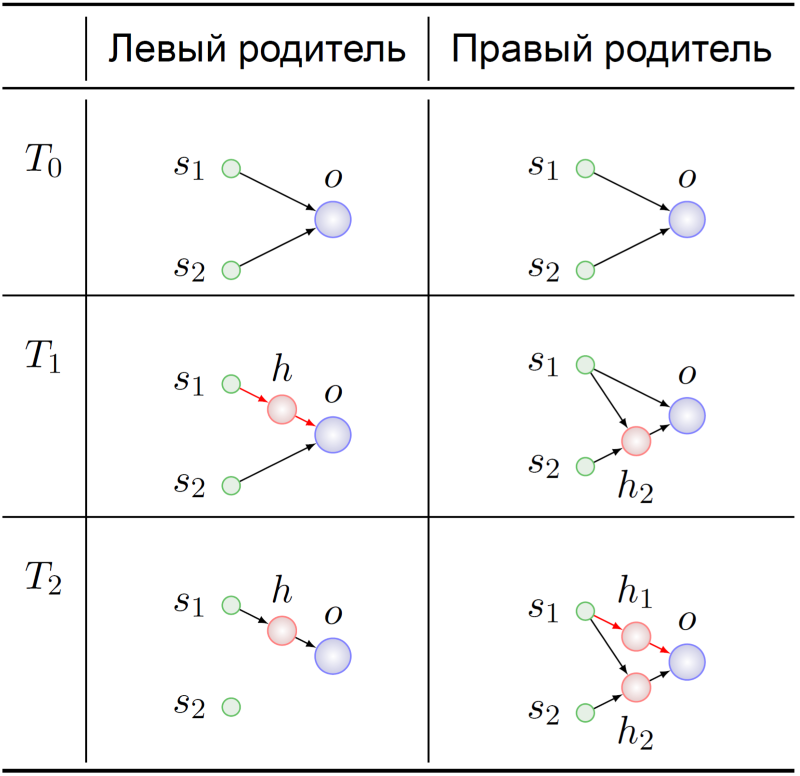
Kedua leluhur dari agen induk mulai, seperti yang diharapkan, dengan NS minimal (T0). Genom mereka bermutasi entah bagaimana di sana, dan pada saat waktu T1 pada leluhur dari orang tua kiri ada penyisipan neuron tersembunyi dalam koneksi s ₁ -> o. Pada saat dramatis ini, gen-gen yang menyandikan ikatan ₁ -> h dan h -> o menemukan maknanya dalam leluhur orangtua kiri: substitusi dari tautan ₁ -> o .
Gen-gen s ₁ -> h ₁ dan h ₁ -> o dalam genotipe induk yang tepat pada saat T ₂ memiliki arti yang persis sama. Nasib lebih lanjut dari nenek moyang kita bukanlah hal yang menarik bagi kita - kita sudah tahu harus bergaul dengan apa:



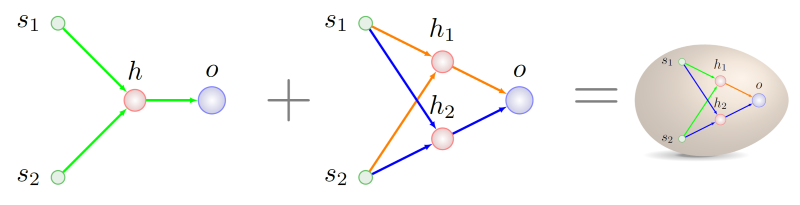
Cara menulis sejarah genetik dengan benar, adalah mungkin untuk melihat waktu berikutnya, terutama karena kami memiliki beberapa temuan kecil di bidang ini, mereka terkait dengan adaptasi teknik asli ke skema reproduksi yang stabil.

Saatnya untuk mengakhiri. Artikel dimulai dengan Youtube - dan kami akan melengkapinya. Dalam versi sebelumnya dari simulator, seorang kolega yang menulis kode untuk menghasilkan lintasan mengakhirinya tanpa apa-apa, jurang maut. Reaksi jaringan saraf yang telah berevolusi untuk waktu yang lama di hadapan cakrawala bumi di bawah roda ke desain alam semesta kecil seperti itu mungkin bisa disebut "templat patah":


Kumpulan luas cerita anekdot lain dari kehidupan cybernaturalists dapat ditemukan di [3] .

Sumber

[1] KO Stanley dan R. Miikkulainen, Evolving Neural Networks melalui Augmenting Topology Evolutionary Computation, vol. 10, tidak. 2, hlm. 99-127, 2002.
[2] C. Green, "Tinjauan Fungsi Aktivasi di SharpNEAT," 19 Juni 2017.
[3] J. Lehman et al, “Kreativitas Yang Mengejutkan dari Evolusi Digital: Kumpulan Anekdot dari Komunitas Evolusi dan Riset Kehidupan Buatan,” arXiv: Neural and Evolutionary Computing, 2018.