
"Blur" pada masyarakat umum adalah efek blur dalam pemrosesan gambar digital. Ini bisa sangat efektif dalam dirinya sendiri, dan sebagai komponen animasi antarmuka, atau efek turunan yang lebih kompleks (bloom / focusBlur / motionBlur). Dengan semua ini, blues jujur di dahi agak lambat. Dan seringkali implementasi yang dibangun pada platform target meninggalkan banyak hal yang diinginkan. Entah kecepatannya menyedihkan, artefaknya melukai mata. Situasi ini menimbulkan banyak implementasi kompromi yang lebih baik atau lebih buruk cocok untuk kondisi tertentu. Implementasi orisinal dengan kualitas keandalan yang baik dan kecepatan tertinggi, sedangkan ketergantungan terendah pada perangkat keras sedang menunggu Anda. Bon appetit!
(Laplace Blur - Nama Algoritma Asli yang Diusulkan)
Hari ini, demoscene internal saya menendang saya dan memaksa saya untuk menulis artikel yang harus ditulis enam bulan lalu. Sebagai seorang amatir, pada waktu luang, untuk mengembangkan algoritma efek asli, saya ingin menawarkan kepada publik algoritma "hampir Gausian blurah", yang ditandai dengan penggunaan instruksi prosesor yang sangat cepat (shift dan masker), dan karenanya dapat diakses untuk implementasi hingga mikrokontroler (sangat cepat dalam lingkungan terbatas).
Menurut tradisi saya menulis artikel tentang Habr, saya akan memberikan contoh dalam JS sebagai bahasa yang paling populer, dan percaya atau tidak, itu sangat nyaman untuk keperluan prototipe algoritma yang cepat. Selain itu, kemampuan untuk mengimplementasikan ini secara efektif pada JS datang dengan mengetik array. Pada laptop saya yang tidak terlalu kuat, gambar layar penuh diproses pada kecepatan 30fps (multithreading pekerja tidak terlibat).
Penafian untuk Matematika KerenSaya akan segera mengatakan bahwa saya melepas topi saya karena saya menganggap diri saya tidak cukup mahir dalam matematika dasar. Namun, saya selalu dibimbing oleh semangat umum dari pendekatan fundamental. Oleh karena itu, sebelum Anda menyontek pendekatan "observasional" saya terhadap aproksimasi, berhati-hatilah dalam menghitung kompleksitas bit dari algoritma, yang, seperti yang Anda pikirkan, dapat diperoleh dengan metode pendekatan polinomial klasik. Saya menebak dengan benar? Anda ingin memperkirakan mereka dengan cepat? Mengingat bahwa mereka membutuhkan aritmatika mengambang, mereka akan secara signifikan lebih lambat daripada satu bit shift, yang akan saya jelaskan pada akhirnya. Singkatnya, jangan terburu-buru ke fundamentalisme teoretis, dan jangan lupa tentang konteks di mana saya memecahkan masalah.
Deskripsi ini hadir di sini bukan untuk menjelaskan jalan pikiran dan dugaan saya yang membawa saya ke hasilnya. Bagi mereka yang tertarik:
Fungsi Gauss asli:
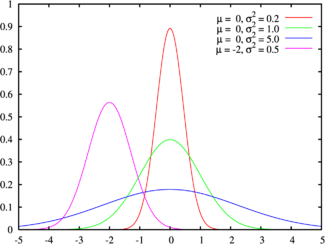
g (x) = a * e ** (- ((xb) ** 2) / c), di mana
a adalah amplitudo (jika kita memiliki delapan bit warna per saluran, maka itu = 256)
e adalah konstanta Euler ~ 2.7
b - pergeseran grafik dalam x (kita tidak perlu = 0)
c - parameter yang mempengaruhi lebar grafik yang terkait dengannya ~ w / 2.35
Fungsi pribadi kami (minus dari eksponen dihapus dengan penggantian perkalian dengan pembagian):
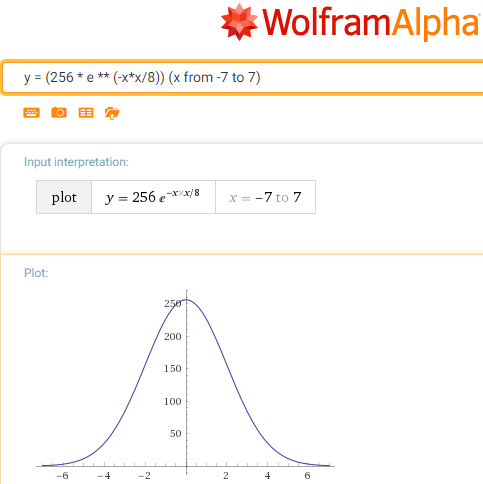
g (x) = 256 / e ** (x * x / c)
Biarkan tindakan perkiraan kotor dimulai:
Perhatikan bahwa parameter c sangat dekat dengan setengah-lebar dan atur 8 (ini disebabkan oleh berapa langkah Anda dapat menggeser satu saluran 8-bit masing-masing).
Kami juga secara kasar mengganti e dengan 2, namun, mencatat bahwa ini mempengaruhi lengkungan "lonceng" lebih dari batasnya. Sebenarnya, ini mempengaruhi 2 / e kali, tetapi yang mengejutkan adalah bahwa kesalahan ini mengkompensasi parameter c, sehingga kondisi batas masih teratur, dan kesalahan hanya muncul dalam "distribusi normal" yang sedikit salah, untuk grafik algoritma, ini akan mempengaruhi dinamika transisi warna gradien, tetapi hampir tidak mungkin untuk dilihat dengan mata.
Jadi sekarang fungsi kita adalah sebagai berikut:
gg (x) = 256/2 ** (x * x / 8) atau gg (x) = 2 ** (8 - x * x / 8)
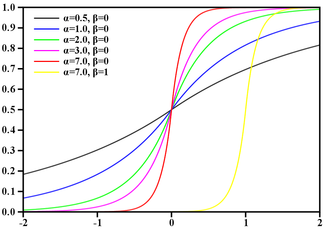
Perhatikan bahwa eksponen (x * x / 8) memiliki kisaran nilai yang sama [0-8] seperti fungsi abs orde lebih rendah (x), oleh karena itu yang terakhir adalah kandidat untuk penggantian. Kami akan segera memeriksa tebakan dengan melihat bagaimana grafik berubah dengannya gg (x) = 256 / (2 ** abs (x)):
GaussBlur vs LaplasBlur:
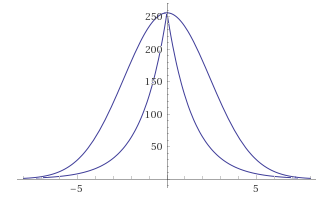
Penyimpangan tampaknya terlalu besar, apalagi fungsinya, setelah kehilangan kelancarannya, kini memiliki puncak. Tapi hei.
Pertama, jangan lupa bahwa kelancaran gradien yang diperoleh dengan blurring tidak tergantung pada fungsi kepadatan probabilitas (yang merupakan fungsi Gauss), tetapi pada integralnya - fungsi distribusi. Pada saat itu, saya tidak tahu fakta ini, tetapi pada kenyataannya, setelah melakukan pendekatan "destruktif" sehubungan dengan fungsi kepadatan probabilitas (Gauss), fungsi distribusi tetap sangat mirip.
Itu:
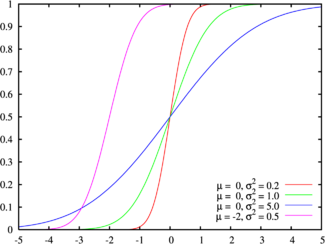
Itu menjadi:
Bukti, diambil dari algoritma yang sudah jadi, bertepatan:
(Ke depan, saya akan mengatakan bahwa kesalahan blur algoritme saya relatif terhadap Gausian x5 hanya 3%).
Jadi, kami telah mendekati fungsi distribusi Laplace. Siapa sangka, tetapi mereka dapat mencuci gambar 97% tidak lebih buruk.
Bukti, perbedaan Gausian blura x5 dan "Laplace blura" x7:

(ini bukan gambar hitam! Anda bisa belajar di editor)
Asumsi transformasi ini memungkinkan kami untuk beralih ke ide untuk mendapatkan nilai dengan penyaringan berulang, yang saya rencanakan untuk dikurangi pada awalnya.
Sebelum memberi tahu algoritma tertentu, akan jujur jika saya berlari ke depan dan segera menggambarkan satu-satunya kelemahannya (meskipun implementasinya dapat diperbaiki dengan kehilangan kecepatan). Tetapi algoritma ini diimplementasikan menggunakan shear arithmetic, dan kekuatan 2 adalah keterbatasannya. Jadi aslinya dibuat untuk mengaburkan x7 (yang dalam tes terdekat dengan Gausian x5). Keterbatasan implementasi ini disebabkan oleh fakta bahwa dengan warna delapan-bit, menggeser nilai dalam drive filter dengan satu bit per langkah, setiap tindakan dari titik berakhir dalam maksimum 8 langkah. Saya juga menerapkan versi yang sedikit lebih lambat melalui proporsi dan tambahan tambahan, yang mengimplementasikan pembagian cepat sebesar 1,5 (menghasilkan radius x15). Tetapi dengan aplikasi lebih lanjut dari pendekatan ini, kesalahan meningkat, dan kecepatan turun, yang tidak memungkinkan untuk digunakan seperti itu. Di sisi lain, perlu dicatat bahwa x15 sudah cukup sehingga tidak memperhatikan perbedaan, hasilnya diperoleh dari aslinya atau dari gambar sampel bawah. Jadi metode ini sangat cocok jika Anda membutuhkan kecepatan luar biasa di lingkungan terbatas.
Jadi, inti dari algoritma ini sederhana, empat lintasan dengan tipe yang sama dilakukan:
1. Setengah dari nilai drive t (awalnya sama dengan nol) ditambahkan ke setengah nilai piksel berikutnya, hasilnya ditugaskan untuk itu. Lanjutkan cara ini ke akhir baris gambar. Untuk semua lini.
Setelah menyelesaikan lintasan pertama, gambar kabur dalam satu arah.
2. Dengan melewati kedua kita melakukan hal yang sama di arah yang berlawanan untuk semua baris.
Kami mendapatkan gambar yang sepenuhnya kabur secara horizontal.
3-4. Sekarang lakukan hal yang sama secara vertikal.
Selesai!
Awalnya, saya menggunakan algoritma dua-pass dengan implementasi back-blur melalui stack, tetapi sulit dimengerti, tidak anggun, dan ternyata lebih lambat pada arsitektur saat ini. Mungkin algoritma one-pass akan lebih cepat pada mikrokontroler, ditambah kemampuan untuk menampilkan hasil secara progresif juga akan menjadi nilai tambah.
Metode implementasi empat arah saat ini, saya melihat Habré dari guru sebelumnya tentang algoritma blur.
habr.com/post/151157 Saya mengambil kesempatan ini untuk mengekspresikan solidaritas dan rasa terima kasih yang mendalam kepadanya.
Tapi peretasan itu tidak berakhir di situ. Sekarang tentang cara menghitung ketiga saluran warna dalam satu instruksi prosesor! Faktanya adalah bahwa bit shift yang digunakan sebagai pembagian oleh dua memungkinkan Anda untuk mengontrol posisi bit hasil dengan sangat baik. Satu-satunya masalah adalah bahwa bit yang lebih rendah dari saluran meluncur ke tetangga yang lebih tinggi, tetapi Anda dapat dengan mudah mengatur ulang, daripada memperbaiki masalah, dengan beberapa kehilangan akurasi. Dan menurut rumus filter yang dijelaskan, penambahan setengah nilai drive dan setengah nilai sel berikutnya (dikenakan pengaturan ulang bit yang dibuang) tidak pernah menyebabkan meluap, jadi Anda tidak perlu khawatir tentang hal itu. Dan rumus filter untuk perhitungan simultan dari semua digit menjadi ini:
buf32 [i] = t = (((t >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F);
Namun, satu tambahan lagi diperlukan: secara eksperimen ditemukan bahwa kehilangan keakuratan dalam rumus ini terlalu signifikan, kecerahan gambar secara visual melonjak secara signifikan. Menjadi jelas bahwa bit yang hilang perlu dibulatkan ke keseluruhan terdekat, dan tidak dibuang. Cara mudah untuk melakukan ini dalam bilangan bulat aritmatika adalah dengan menambahkan setengah pembagi sebelum pembagian. Pembagi kami adalah dua, jadi Anda harus menambahkan satu, dalam semua digit, - konstanta 0x010101. Tetapi dengan tambahan apa pun, seseorang harus waspada mendapatkan luapan. Jadi kita tidak bisa menggunakan koreksi semacam itu untuk menghitung setengah nilai sel berikutnya. (Jika ada warna putih, kami akan mendapatkan overflow, oleh karena itu kami tidak akan memperbaikinya). Tapi ternyata kesalahan utama dibuat oleh beberapa divisi drive, yang bisa kita perbaiki. Karena, pada kenyataannya, bahkan dengan koreksi seperti itu, nilai dalam drive tidak akan naik di atas 254. Tetapi ketika ditambahkan ke 0x010101, overflow tidak akan dijamin. Dan rumus filter dengan koreksi mengambil bentuk:
buf32 [i] = t = ((((((0x010101 + t) >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F);
Bahkan, rumus melakukan koreksi dengan cukup baik, jadi ketika Anda berulang kali menerapkan algoritme ini pada gambar, artefak mulai terlihat hanya dalam sepuluh lintasan kedua. (bukan fakta bahwa mengulang blura Gausian tidak akan menghasilkan artefak seperti itu).
Selain itu, ada properti indah dengan banyak tiket masuk. (Ini bukan karena algoritma saya, tetapi karena "normalitas" dari distribusi normal). Sudah di pass kedua Laplace Blura, fungsi kepadatan probabilitas (jika saya pikir semuanya benar) akan terlihat seperti ini:
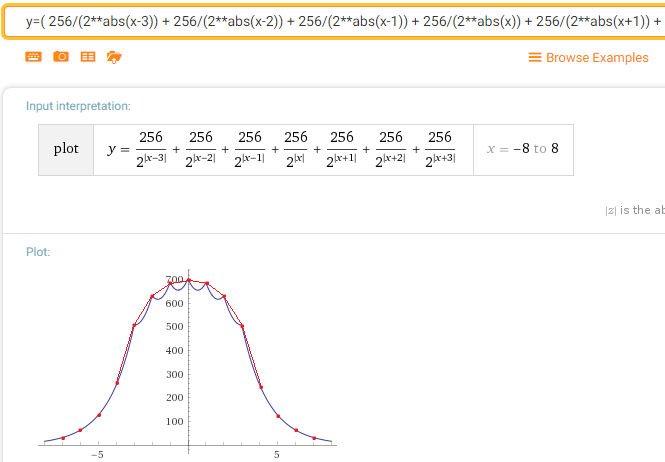
Yang, Anda lihat, sudah sangat dekat dengan Gaussian.
Secara empiris, saya menemukan bahwa menggunakan modifikasi dengan radius besar diperbolehkan berpasangan, karena properti yang dijelaskan di atas mengkompensasi kesalahan jika pass terakhir lebih akurat (yang paling akurat adalah algoritma blur x7 yang dijelaskan di sini).
demorapcodpenDaya tarik untuk ahli matematika keren:
Apa yang menarik untuk mengetahui seberapa benar menggunakan filter secara terpisah, saya tidak yakin apakah ada gambar distribusi simetris. Meskipun heterogenitas mata tidak terlihat.
upd: Di sini saya akan meningkatkan tautan yang bermanfaat, yang disajikan dengan baik oleh komentator, dan ditemukan dari Khabrovit lainnya.
1. Cara kerja master intel, dengan mengandalkan kekuatan SSE -
software.intel.com/en-us/articles/iir-gaussian-blur-filter-implementation-using-intel-advanced-vector-extensions (terima kasih
vladimirovich )
2. Basis teoretis pada topik "Konvolusi gambar cepat" + beberapa aplikasi khusus sehubungan dengan Gaussian bluer yang jujur -
blog.ivank.net/fastest-gaussian-blur.html (terima kasih
Grox )
Saran, komentar, kritik konstruktif dipersilahkan!