Verifikasi numerik hipotesis abc (ya, yang itu)

Hai, Habr.

Sudah ada beberapa artikel tentang hipotesis abc di Geektimes Habr (misalnya, pada 2013 dan 2018 ). Cerita itu sendiri tentang sebuah teorema yang pada awalnya tidak dapat dibuktikan selama bertahun-tahun, dan kemudian tidak dapat diverifikasi untuk jumlah tahun yang sama, tentu layak setidaknya film layar lebar. Tetapi dalam bayang-bayang kisah yang indah ini, teorema itu sendiri dianggap terlalu dangkal, meskipun tidak kalah menarik. Setidaknya dengan fakta bahwa hipotesis abc adalah salah satu dari beberapa masalah sains modern yang tidak terpecahkan, pernyataan masalah yang bahkan dapat dipahami oleh siswa kelas lima. Jika hipotesis ini benar, maka dengan mudah mengikuti dari bukti teorema penting lainnya, misalnya, bukti teorema Fermat .

Tanpa mengklaim kemenangan Motizuki, saya juga memutuskan untuk mencoba dan memutuskan untuk memeriksa dengan komputer berapa banyak persamaan yang dijanjikan dalam hipotesis terpenuhi. Sebenarnya, mengapa tidak - prosesor modern tidak hanya untuk bermain game - mengapa tidak menggunakan komputer untuk tujuan utama (menghitung) ...

Siapa peduli apa yang terjadi, tolong, di bawah kucing.

Pernyataan masalah

Mari kita mulai dari awal. Tentang apa teorema itu? Seperti yang dikatakan Wikipedia (kata-kata dalam versi bahasa Inggris sedikit lebih jelas), untuk saling sederhana (tidak memiliki pembagi umum) angka a, b dan c sedemikian sehingga a + b = c, untuk setiap ε> 0 ada jumlah triples a + b yang terbatas = c, sedemikian rupa sehingga:



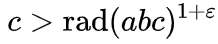
Fungsi rad disebut radikal , dan menunjukkan produk dari faktor prima suatu bilangan. Misalnya, rad (16) = rad (2 * 2 * 2 * 2) = 2, rad (17) = 17 (17 adalah bilangan prima), rad (18) = rad (2 * 3 * 3) = 2 * 3 = 6, rad (1.000.000) = rad (2 ^ 6 ⋅ 5 ^ 6) = 2 * 5 = 10.

Sebenarnya, inti dari teorema ini adalah bahwa jumlah tiga kali lipat semacam itu cukup kecil. Sebagai contoh, jika kita mengambil secara acak ε = 0,2 dan persamaan 100 + 27 = 127: rad (100) = rad (2 * 2 * 5 * 5) = 10, rad (27) = rad (3 * 3 * 3) = 3, rad (127) = 127, rad (a * b * c) = rad (a) * rad (b) * rad (c) = 3810, 3810 ^ 1.2 jelas lebih besar dari 127, ketidaksetaraan tidak berlaku. Tetapi ada pengecualian, misalnya, untuk kesetaraan 49 + 576 = 625, kondisi teorema terpenuhi (mereka yang ingin dapat memeriksa sendiri).

Momen kunci berikutnya bagi kita adalah sejumlah persamaan ini, menurut teorema. Yaitu ini berarti Anda bisa mencoba memilah semuanya di komputer. Sebagai hasilnya, ini memberi kita Hadiah Nobel tugas pemrograman yang cukup menarik.

Jadi mari kita mulai.

Kode sumber

Versi pertama ditulis dalam Python, dan meskipun bahasa ini terlalu lambat untuk perhitungan seperti itu, menulis kode di atasnya mudah dan sederhana, yang nyaman untuk pembuatan prototipe.

Mendapatkan radikal : kami menguraikan angka menjadi faktor prima, lalu menghapus pengulangan, mengubah array menjadi satu set. Kemudian dapatkan produk dari semua elemen.

def prime_factors(n): factors = [] # Print the number of two's that divide n while n % 2 == 0: factors.append(int(2)) n = n / 2 # n must be odd at this point so a skip of 2 ( i = i + 2) can be used for i in range(3, int(math.sqrt(n)) + 1, 2): # while i divides n , print i ad divide n while n % i == 0: factors.append(int(i)) n = n / i # Condition if n is a prime number greater than 2 if n > 2: factors.append(int(n)) return set(factors) def rad(n): result = 1 for num in prime_factors(n): result *= num return result 

Bilangan prima yang saling menguntungkan : faktor-faktor angka, dan cukup periksa persimpangan set.

 def not_mutual_primes(a,b,c): fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c) return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0 

Periksa : kami menggunakan fungsi yang sudah dibuat, semuanya sederhana di sini.

 def check(a,b,c): S = 1.2 # Eps=0.2 if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c): print("{} + {} = {} - PASSED".format(a, b, c)) else: print("{} + {} = {} - FAILED".format(a, b, c)) check(10, 17, 27) check(49, 576, 625) 

Mereka yang ingin dapat bereksperimen secara mandiri dengan menyalin kode di atas ke editor bahasa Python online. Tentu saja, kode berjalan seperti yang diharapkan, dan menghitung semua tiga kali lipat untuk setidaknya satu juta akan terlalu lama. Di bawah spoiler ada versi yang dioptimalkan, disarankan untuk menggunakannya.

Versi terakhir ditulis ulang dalam C ++ menggunakan multithreading dan beberapa optimasi (bekerja di C dengan set berpotongan akan terlalu hardcore, meskipun mungkin lebih cepat). Kode sumber berada di bawah spoiler, dapat dikompilasi dalam kompiler g ++ gratis, kode tersebut bekerja di bawah Windows, OSX dan bahkan pada Raspberry Pi.


Bagi mereka yang terlalu malas untuk menginstal kompiler C ++, disediakan versi Python yang sedikit dioptimalkan, yang dapat dijalankan di editor online mana pun (saya menggunakan https://repl.it/languages/python ).

Hasil

Tiga kali lipat a, b, c benar-benar sangat sedikit.

Beberapa hasil diberikan di bawah ini:
N = 10 : 1 “tiga”, lead time <0,001c
1 + 8 = 9

N = 100 : 2 “tiga kali lipat”, runtime <0,001c
1 + 8 = 9
1 + 80 = 81

N = 1000 : 8 "tiga kali lipat", runtime <0,01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625

N = 10.000 : 23 "tiga kali lipat", runtime 2s


N = 100000 : 53 tiga kali lipat, runtime 50c


Dengan N = 1.000.000, kami hanya memiliki 102 "tiga kali lipat", daftar lengkap diberikan di bawah spoiler.


Sayangnya, program masih berjalan lambat, saya tidak menunggu hasil untuk N = 10.000000, waktu perhitungan lebih dari satu jam (mungkin saya membuat kesalahan dengan optimasi algoritma di suatu tempat, dan saya bisa melakukan yang lebih baik).

Yang lebih menarik untuk melihat hasilnya secara grafis:



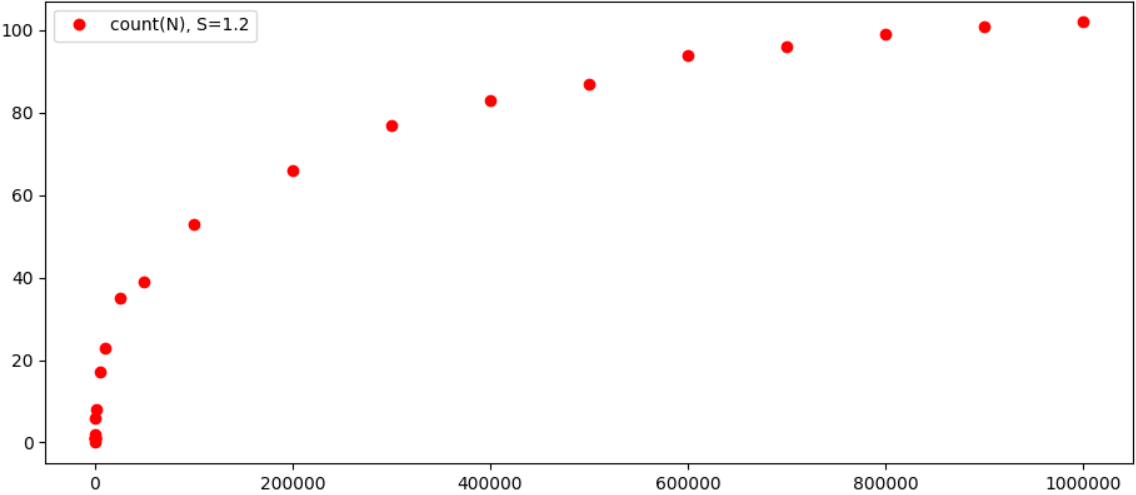
Pada prinsipnya, sangat jelas bahwa ketergantungan dari jumlah tiga kali lipat yang mungkin pada N tumbuh terasa lebih lambat daripada N itu sendiri, dan kemungkinan hasilnya akan konvergen ke beberapa nomor tertentu untuk setiap ε. Ngomong-ngomong, dengan peningkatan ε, jumlah "tiga kali lipat" menurun secara nyata, misalnya, untuk ε = 0,4 kita hanya memiliki 2 persamaan untuk N <100000 (1 + 4374 = 4375 dan 343 + 59049 = 59392). Jadi secara umum, tampaknya teorema itu benar-benar berlaku (well, dan mungkin itu sudah diuji pada komputer yang lebih kuat, dan mungkin semua ini sudah lama dihitung).

Mereka yang ingin dapat bereksperimen sendiri, jika ada yang memiliki hasil untuk angka 10.000.000 dan lebih tinggi, saya akan dengan senang hati menambahkannya ke artikel. Tentu saja, akan menarik untuk "menghitung" sampai saat ketika set "tiga kali lipat" benar-benar berhenti tumbuh, tetapi bisa memakan waktu yang sangat lama, kecepatan perhitungan tampaknya tergantung pada N sebagai N * N (atau mungkin N ^ 3), dan prosesnya sangat panjang Namun demikian, hal yang luar biasa ada di dekatnya, dan mereka yang berharap dapat bergabung dengan pencarian.

Sunting: seperti yang disarankan dalam komentar, Wikipedia sudah memiliki tabel dengan hasil - dalam kisaran N hingga 10 ^ 18 jumlah "tiga kali lipat" masih terus bertambah, sehingga "akhir" set belum ditemukan. Semua lebih menarik - intriknya masih dipertahankan.