Pada bulan Maret 2016, Robert J. Lemke-Oliver dan Kannan Sundararajan dari Stanford University
membuka pola baru dalam distribusi bilangan prima. Ternyata bilangan prima secara
khusus didistribusikan melalui ruang angka. Untuk lebih jelasnya lihat terjemahan artikel
"Struktur dan keacakan bilangan prima" di Habré.
Para ahli dari bidang lain, termasuk kimia, bergabung dalam studi topik. Dan berhasil. Profesor Kimia Teoritis
Salvatore Torcuato, bersama dengan ahli teori bilangan
Matthew de Courcy-Irlandia, menemukan
pola baru dalam distribusi bilangan prima yang sebelumnya tidak diketahui. Ternyata distribusi bilangan prima membentuk pola difraksi seperti fraktal, agak mirip dengan pola difraksi kristal kuasi eksotis.
Profesor Torcuato mengkhususkan diri dalam studi pola dalam struktur sistem fisik, seperti kristal dan koloid. Cara standar untuk mempelajari struktur adalah difraksi sinar-X. Molekul acak dalam cairan atau gas memantulkan sinar ke segala arah tanpa menciptakan pola yang nyata. Tetapi atom-atom yang terletak secara simetris dalam kristal secara serempak memantulkan gelombang cahaya, menciptakan titik terang periodik difraksi yang diucapkan (
puncak Bragg ). Analisis puncak Bragg memungkinkan untuk memahami struktur internal kristal atau bahan lain yang menciptakan gambar seperti itu.
Jadi, dalam artikel ilmiah baru oleh Torkuato dan lain-lain (
1 ,
2 ,
3 ) ditunjukkan bahwa struktur terurut yang ditemukan dalam distribusi bilangan prima tidak lebih dari pola difraksi seperti fraktal, mirip dengan kristal quasicrystals.
Gambar puncak Bragg pada kisi bilangan prima mirip dengan kristal kuasi, tetapi masih berbeda dari mereka. Torcuato
mengatakan bahwa bilangan prima sebagai sistem fisik "adalah kategori struktur yang sama sekali baru." Para peneliti menyebut pola fraktal seperti baru ini "batas-periodisitas efektif".
Angka tersebut terdiri dari urutan periodik puncak terang yang mencerminkan interval bilangan prima yang paling umum: semuanya aneh (kecuali 2), banyak yang bersebelahan. Puncak yang paling terang (pasangan dipisahkan oleh dua digit) bergantian secara berkala dengan puncak yang kurang cerah, yang mencerminkan bilangan prima yang dipisahkan oleh enam digit. Di antara mereka ada puncak yang lebih redup yang berhubungan dengan pasangan bilangan prima yang lebih jauh, dll. Semua ini adalah jumlah puncak Bragg yang tak terbatas yang ditempatkan di dalam satu sama lain.
Struktur serupa dari puncak Bragg diamati sebelumnya - dalam pola difraksi kristal quasicry.
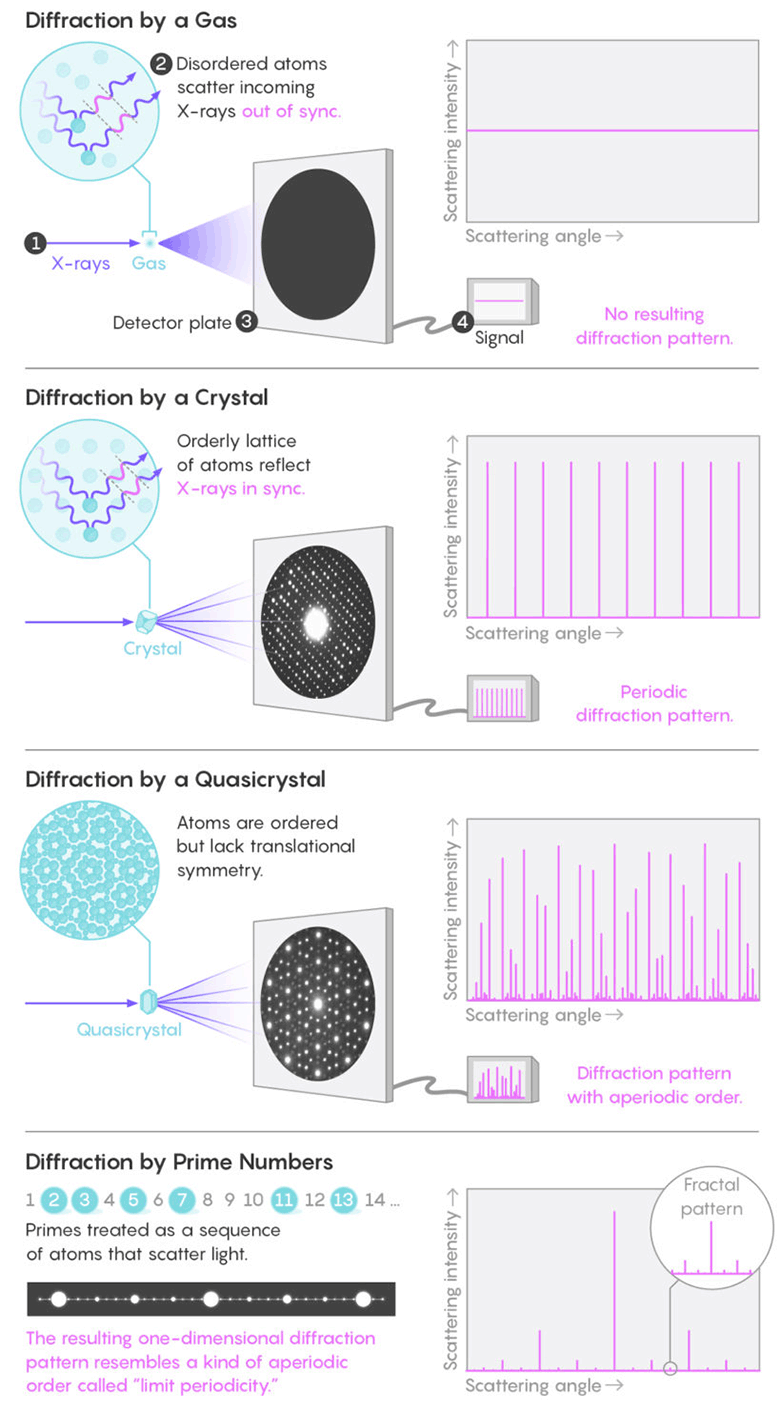Molekul acak dalam cairan atau gas memantulkan sinar ke segala arah tanpa menciptakan pola yang nyata. Tetapi atom-atom yang terletak secara simetris dalam kristal secara serempak memantulkan gelombang cahaya, menciptakan bintik-bintik terang periodik dari difraksi yang diucapkan. Ternyata, pola distribusi bilangan prima membentuk pola difraksi fraktal, mirip dengan quasicrystalsQuasicrystals adalah bahan aneh yang ditemukan pada 1980-an. Mereka dicirikan oleh simetri terlarang dalam kristalografi klasik dan adanya keteraturan jarak jauh. Mosaik aperiodik dari jenis
mosaik Penrose yang terkenal adalah model matematika kristal quasicry. Dalam mosaik ini, simetri translasi tidak ada, pengulangan dan quasicrystallinity hadir (simetri urutan kelima).
Fragmen Penrose mosaik tipe P1 (dari ubin enam jenis)Dalam kasus bilangan prima, jarak antara puncak sebanding satu sama lain, berbeda dengan puncak Bragg spasi quasicrystals yang tidak beraturan. "Bilangan prima sebenarnya menyiratkan keadaan posisi partikel yang sama sekali berbeda, mirip dengan kristal kuasi, tetapi tidak seperti kristal kuasi,"
kata Torcuato.
Penemuan pola difraksi tidak dapat disebut penemuan terobosan untuk teori bilangan, karena sebagian besar dari pola-pola ini telah dijelaskan sebelumnya, hanya dengan metode matematika lainnya (bukan melalui difraksi kristal quasicrystals). Jadi, dengan menggunakan pola difraksi, dimungkinkan untuk memprediksi "ganda" dari tipe 17 dan 19 - ini adalah persamaan matematika dari
hipotesis Hardy - Littlewood pertama mengenai keberadaan tupel bilangan prima pada segmen tertentu dari garis bilangan. Salah satu aturan melarang kembar tiga dari angka ganjil berturut-turut setelah {3, 5, 7}. Ini juga menjelaskan mengapa puncak Bragg paling terang berikutnya dalam pola difraksi sesuai dengan angka yang dipisahkan oleh enam digit daripada empat.
Sebuah karya ilmiah baru hanyalah pandangan baru pada masalah distribusi prima yang seragam dan cara yang lebih mudah untuk memperoleh "hukum tunggal" tertentu untuk mereka. Selain itu, ini adalah cara yang tidak biasa menganalisis masalah matematika dari sudut pandang kristalografi, yaitu dari sudut pandang bidang penelitian yang relatif muda yang disebut "urutan aperiodik", yang mempelajari model yang tidak berulang dan terletak di persimpangan kristalografi, sistem dinamis, analisis harmonik, dan geometri diskrit. Cabang ilmu pengetahuan ini tumbuh setelah penemuan kristal kuasi, ketika menjadi jelas bahwa metode lama tidak bekerja di sini.
Distribusi bilangan prima menyerupai tatanan aperiodik khusus, yang dikenal sejak 1950-an. Ini disebut batas periodisitas. Dalam sistem seperti itu, interval periodik bersarang dalam hierarki yang tak terbatas, sehingga dalam setiap interval, sistem berisi bagian dari pola yang diulang hanya dalam interval yang lebih besar, seperti pada ubin Taylor-Sokolar.
Taylor-Sokolar TilePerhitungan teoritis menunjukkan bahwa fase periodik maksimum suatu zat harus dapat terbentuk di alam, dan sistem tersebut mungkin memiliki sifat yang tidak biasa. Tetapi tidak ada yang menduga untuk menghubungkan periodisitas pembatas dengan bilangan prima. Sekarang kita tahu bahwa ada koneksi seperti itu, dan bilangan prima menunjukkan jenis baru periodisitas batas - periodisitas "efektif" batas, karena sinkronisasi dalam jarak antara bilangan prima di seluruh sistem hanya diamati secara statistik.
Timbul pertanyaan: bagaimana bisa pola dalam distribusi bilangan prima mempengaruhi kekuatan algoritma kriptografi?
“Saya mendapatkan banyak sekali surat tentang hal ini. Meskipun ini adalah studi yang menarik, itu tidak ada hubungannya dengan kriptografi, ”
tulis ahli kriptografi terkenal Bruce Schneier di blog-nya. - Cryptographers tidak tertarik untuk mencari bilangan prima atau bahkan distribusinya. Kegigihan algoritma kriptografi kunci publik tipe RSA dikaitkan dengan kesulitan memfaktorkan bilangan komposit besar, yang merupakan produk dari bilangan prima. Dan ini adalah masalah yang sangat berbeda. "
Jadi, meskipun ada kemajuan dalam mempelajari distribusi bilangan prima, tidak perlu khawatir tentang kekuatan kode kriptografi.
