Masalah penulisan teks matematika modern

Dalam sebuah artikel baru-baru ini, kawan KvanTTT mengajukan pertanyaan :

Bisakah Anda menjelaskan apa yang tidak Anda sukai tentang rumus modern (pernyataan matematika dan) dan bagaimana hal itu dapat diperbaiki?

Saya mencoba menjawab dalam satu komentar, tetapi ukuran bidang teks tidak memungkinkan saya untuk menyelesaikan perhitungan. Artikel ini adalah jawaban yang terlalu rinci.

Saya harus mengatakan, materinya holivarny. Sebagian terlalu emosional. Sangat kontroversial. Terlalu pribadi - seringkali berdasarkan pengalaman pribadi, tidak kaya, meski beragam. Pos tersebut berkaitan dengan buku teks sekolah dan universitas: literatur "profesional" memiliki kekhususannya sendiri, audiensnya sendiri. Tidak ada solusi untuk masalah dalam realitas saat ini. Pada saat yang sama, beberapa pengamatan saya jauh sebelum saya diungkapkan oleh otoritas seperti Knut dan Hamming; orang yang sedikit kurang populer bahkan membasuh instruksi " Cara membaca matematika ".

Jadi, menurut pendapat saya, keluhan utama adalah tidak banyak menulis formula untuk presentasi materi . Apalagi untuk penyajian materi di hampir semua jenjang pendidikan, mulai dari sekolah dan diakhiri dengan ilmu yang maju. Awal dari situasi saat ini diletakkan oleh Euclid, yang menyatakan tidak adanya jalan kerajaan dalam matematika. Jalan kerajaan belum diaspal sejauh ini. Euclid melakukannya, dan kita bisa.

Masalah pertama adalah pentingnya tidak ditampilkan . Hadiah lain dari Euclid: "Beri penny satu sen dolar jika dia mencari manfaat, bukan matematika." Para penulis mulai memperkenalkan definisi, membuktikan teorema, dan melakukan matematika lain tanpa menjelaskan mengapa itu diperlukan sama sekali. Contoh: buku teks tentang analisis matematika dari Fichtenholtz . Baca bab pertama: "dari kursus sekolah Anda tahu tentang bilangan rasional, tetapi kebutuhan matematika memaksa kita untuk memperkenalkan bilangan real ..." dan itu dimulai. Apa saja kebutuhan, matematika macam apa, mengapa rasional tidak bahagia - ya, anjing mengenalnya. "Jelas sekali."

Atau contoh lain dari tutorial yang sama. "Angka konstan a disebut batas opsi $$ jika untuk setiap positif $$ tidak peduli seberapa kecilnya, ada angka N sehingga semua nilainya $$ di mana angka n> N memenuhi kesetaraan $$ . "

Sebagian besar siswa tidak mengerti definisi di atas, tetapi setelah enam bulan mereka terbiasa. Bahkan lebih banyak siswa, bahkan menjelang akhir studi mereka, tidak menyadari mengapa mereka membutuhkan konsep batas urutan. Demikian pula untuk fungsi, integral, seri ... Fichtenholtz menjelaskan beberapa objek matematika, terkadang memberikan contoh-contoh khusus - dan itu saja. Nah, ya, sekarang saya mengerti bahwa batasan diperlukan, misalnya, untuk deskripsi yang benar dari jumlah atas / bawah ketika memperkenalkan integral, tetapi sebelum integral dua semester lagi!

Atau penentu yang didefinisikan sebagai fungsi multilinear miring-simetris. Kawan, apa kamu serius? Satu-satunya tanggapan yang memadai dari siswa tahun pertama terhadap definisi "jadi apa"? Apa manfaat dari definisi ini? Saya tidak berdebat, ada manfaatnya, tetapi bisakah mahasiswa baru menyadarinya?

Solusi salah untuk masalah : latar belakang. Itu muncul di semua jenis konferensi. "Masalahnya ditimbulkan oleh Yakub, diperiksa oleh muridnya Habel, dan murid Kain murid, dan seratus lima ratus inkarnasi Wisnu." Apa esensi dari masalah, mengapa diselesaikan oleh penulis asli, mengapa begitu penting untuk membunuh jam profesor di dalamnya - dihilangkan.

Masalah selanjutnya - penulis tidak menimbulkan masalah nyata

Pada prinsipnya, ini mirip dengan yang sebelumnya. Ingat jalannya teori probabilitas. Tugas apa yang ada di sana? "Ada 25 bola hitam dan 10 bola putih di keranjang ..." Contoh kasino, kartu, D & D, ekonomi - tidak, tidak terdengar. Kami akan menggunakan contoh yang paling benar secara politis, meskipun teori probabilitas telah tumbuh dari penelitian dadu.

Tentang contoh langsung baru-baru ini menulis Free_Mic_RS


Matematika dimulai dengan tugas. Dan tugas sepihak yang mati meninggalkan kesan bahwa teori itu hanya bekerja dengan mereka. Niat penulis baik: untuk memberi contoh, dan kemudian beralih ke umum. Abstrak dari contoh. Tetapi beberapa contoh "hidup" akan membuat transisi ke abstraksi jauh lebih bermanfaat. Setidaknya, saya sangat percaya bahwa proses sebaliknya (transisi dari abstrak ke khusus) akan jauh lebih mudah.

Masalah: keringkasan dan ketidakkonsistenan yang berlebihan

Ingat sekolah? Bagaimana dengan formula diskriminan? Dan bagaimana itu dibuktikan / diturunkan? Salah satu caranya: murni aljabar . Kami mengambil persamaan $$ , “Kalikan setiap bagian dengan $$ dan tambahkan $$ "( Mengapa tepatnya nilai-nilai ini? ), Beberapa transformasi lagi - dan Anda selesai. Setelah diskriminan, siswa diberikan diskriminan-untuk-genap b. Dan kemudian formula Vieta. Dan juga kotak penuh. Dan banyak contoh. Dan jauh dari selalu menjelaskan mengapa semua metode ini diperlukan.

Sekarang bayangkan situasinya, siswa diberi tahu: “hari ini kita akan belajar bagaimana menyelesaikan persamaan $$ . Apa saja. ” Dan serangkaian contoh dimulai dengan komplikasi.

$$

Banyak contoh yang secara organik mengarah pada solusi persamaan melalui kuadrat penuh. Kemudian Anda dapat memasukkan diskriminan (sebagai algoritme sederhana untuk menyelesaikan persamaan ketika siswa bosan menyoroti kuadrat penuh), dan Viet dengan diskriminan yang bahkan sebagai "tahu-bagaimana."

Pendekatan serupa digunakan dalam buku pelajaran. Sayangnya, tidak semuanya. Dan tidak di mana-mana urutan yang jelas terlihat. Menurut rumor, beberapa penulis kehilangan draft sheet dalam trem, dan kemudian mengganti potongan yang hilang dengan ekspresi seperti "mudah untuk menunjukkan itu ...". Akibatnya, alih-alih tenang melompat dari contoh ke contoh, siswa dipaksa untuk melompati jurang. Berapa banyak orang yang putus sekolah dan masih istirahat selama 10 + 6 tahun sekolah / universitas?

Contoh pribadi (diminta di pos asli). Pada tahun pertama matan, saya menderita. Diam-diam memecahkan contoh, dia tidak belajar teori sama sekali. Saya meminta bantuan teman sekelas untuk menghitung panjang kurva melalui integral. Dia mengambil sebotol bir, menggambar lengkungan acak, meluruskannya dengan segmen yang sangat kecil, memilih satu segmen seperti itu, membangunnya hingga segitiga dl, dx, dy, dan bertanya: "Apakah Anda ingat teorema Pythagoras"? Kemudian semuanya sederhana.



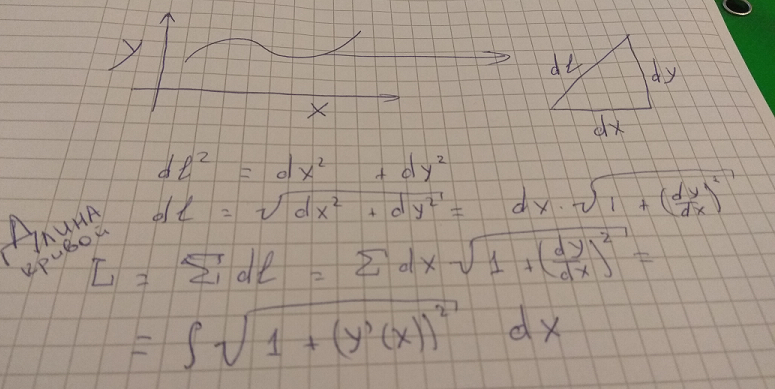
Saya bertanya kepadanya: mengapa ini tidak ditampilkan secara berpasangan / dalam buku teks? Dia menunjukkan beberapa contoh tandingan, menjelaskan mengapa formalisme diperlukan dalam matan - dan saya menjadi macet. Saya baru saja membaca teorema, menyoroti hal utama, menulis / memecahkan contoh-contoh sepele, kemudian berurusan dengan formalisme - dan benar-benar mengerti apa yang sedang terjadi.

Saya tidak tahu apakah mungkin untuk secara besar-besaran menggunakan pendekatan tinjauan umum => counterexamples => formalisme . Saya tidak tahu berapa banyak dan teori / praktik apa yang perlu diperoleh siswa sebelum "terobosan", saya tidak bisa membayangkan bagaimana cara menempatkan eksperimen pedagogis pada topik ini, dan berapa banyak pekerjaan yang harus saya investasikan dalam penelitian. Tetapi memori dari penjelasan itu telah hidup selama 10 tahun. Dan setelah bertahun-tahun, saya mencoba memberikan audiens gambaran besar pertama, kemudian menunjukkan masalahnya, dan kemudian terjun ke detail.

Anda akan mengatakan perasaan pribadi saya mungkin salah. Selain mereka, saya hanya punya ide serupa dari Hamming :

... Saya bisa mempelajari metode mana yang efektif dan mana yang tidak. Saat menghadiri pertemuan, saya sudah mempelajari mengapa beberapa karya diingat, dan sebagian besar tidak. Seseorang teknis ingin memberikan kuliah teknis yang sangat terbatas. Sebagai aturan, audiens menginginkan kuliah umum yang bersifat umum dan menginginkan gambaran dan pengenalan yang jauh lebih umum daripada yang ingin disampaikan oleh pembicara. Akibatnya, banyak ceramah tidak efektif. Dosen memanggil topik dan tiba-tiba menyelami rinciannya. Hanya sedikit orang yang bisa melacak. Anda harus menggambar gambaran besar untuk mengatakan mengapa ini penting, dan kemudian perlahan membuka sketsa dari apa yang dilakukan. Kemudian lebih banyak orang akan berkata: "Ya, Joe yang melakukannya" atau "Mary melakukan apa yang benar-benar saya lihat tentang apa itu. Ya, Mary memberikan kuliah yang sangat bagus, saya mengerti apa yang dia lakukan. " Sebagai aturan, orang memberikan ceramah yang sangat terbatas dan aman; biasanya tidak efektif. Selain itu, banyak kuliah diisi dengan informasi ...

Gagasan massal

Saya harus mengatakan, pengalaman saya dalam mengajar sangat terbatas. Anda mungkin telah memperhatikan bahwa saya membatasi diri pada kurikulum sekolah dan matanaliz. Sayangnya, ini adalah area di mana saya memiliki kesempatan untuk berhubungan teori dengan praktik. Saya masih belum mengerti esensi dari penentu dalam aljabar, saya tidak menyadari geometri projektif, dan hanya enam bulan yang lalu saya mulai menembus matriks (tepat setelah latihan, ya). Sebuah ilustrasi bagus tentang ungkapan "teori tanpa praktik sudah mati."

Seperti yang saya diberitahu, di NMU konsep baru selalu diperkenalkan dengan selusin pertanyaan. Bagaimana kalau begitu? Dan jika klausa ini tidak terpenuhi? Apa yang dibutuhkan untuk melengkapi konsep kami menjadi sebuah semi-grup? Pendengar diizinkan bermain dengan subjek. Biasakan untuk itu. Saya pikir perlu memikirkan dengan hati-hati tentang pengalaman NMU.

Tentunya, di cabang matematika yang lebih tinggi, pendekatan "pertama contoh, lalu abstraksi" tidak akan berfungsi. Jadi, contoh pada selembar kertas tidak membantu mewujudkan RSA. Tetapi meningkatnya waktu program dengan bertambahnya panjang kunci membantu untuk merasakan aspek-aspek praktis semata.

Ada ketakutan bahwa buku sekolah "ideal / rumah kaca" akan mengarah ke kejutan ketika bekerja dengan "menara". Sepertinya, "seorang pekerja keras harus dididik sejak usia muda."

Cukup sulit untuk mengembangkan kursus, berharap siswa sudah tahu sesuatu. Semakin besar basis yang dibutuhkan, semakin besar kemungkinan sesuatu dari basis itu disalahpahami oleh siswa.

Mereka mengatakan bahwa puncak bentuk ahli matematika berusia 30 tahun. Setelah 30, Anda sudah dapat memuatnya untuk menulis buku teks, memberi pasangan ahli metodologi.

Teknologi saat ini memungkinkan Anda untuk menulis teks menggunakan git. Artikel tentang mengkompilasi TeXa dalam pdf dalam proses CI baru-baru ini tergelincir pada hub Saya yakin bahwa tim penulis dengan alat yang bagus dapat menulis buku pelajaran yang jauh lebih baik.

Selain profesor, guru, siswa, dan anak sekolah, ada beberapa kondisi dalam matematika. Dan peraturan. Dan persyaratannya. Dan sertifikasi. Semua ini mempengaruhi buku teks, penulis, guru, dan kualitas materi.

Cara meningkatkan aliran materi dalam teks matematika

Dalam realitas (Rusia) saat ini - tidak ada. Ada penggemar, ada profesional, tidak ada motivasi.

Profesor matematika memiliki cukup tugas untuk menulis buku teks. Terkadang tidak ada keterampilan kemanusiaan murni, buku tidak diajarkan di universitas. Plus, deformasi profesional: "jelas" untuk seorang profesor bisa sangat besar bagi siswa. Guru matematika sibuk. Dan kertas. Dan les. Saya tidak akan mengatakan apa-apa tentang negara. Hampir tidak menemui wakilnya, jadi tidak ada yang bisa dikatakan. Kecuali saya menyebutkan kebijakan penggantian buku teks setiap tiga tahun. Setelah sekolah, saya ingin membawa buku pelajaran saya ke perpustakaan, mereka mengatakan kepada saya "mereka sudah tua, kamu tidak bisa menyimpannya." Motivasi untuk menulis buku teks yang bagus tidak menambah pendekatan ini.

Dengan kata lain, saya pribadi tidak mengharapkan kemajuan positif dari sistem pendidikan. Saya berharap, tentu saja, tetapi saya tidak menunggu. Apa yang membantu adalah sekilas tentang IT dan teknik lainnya. Di salah satu konferensi matematika, saya menerima buku tentang grafik komputer dari salah satu peserta. Penulis bekerja di kantor yang mengembangkan inti grafis dari beberapa sistem gambar, dan materinya cukup bagus. Matematika tidak “murni”, diterapkan, tetapi fakta keberadaan materi pendidikan yang baik tentu menyenangkan.

Pendekatan lain: guru dari perusahaan yang bekerja di universitas. Teks-teks matematika dari orang-orang ini tidak dapat diharapkan, spesifikasinya tidak sama. Kecuali jika pengembang game akan menulis manual tentang teorinya, atau grafik akan menulis tentang aljabar / geometri yang diperlukan untuk mengembangkan sistem CAD yang sama (jika ada proyek seperti itu - panggil) .

Akhirnya, ada berbagai platform pendidikan non-negara, seperti Coursera yang sama. Orang-orang ini dapat melakukan apa saja, karena mereka bekerja demi uang, bersaing, dan dengan cepat menerima umpan balik. Tetapi mereka memiliki kelemahannya sendiri: format untuk mengirimkan data berbeda. Mereka tidak menulis teks secara langsung.

Dan apa yang akan terjadi di masa depan?

Paling menarik. Mungkin semuanya akan tetap seperti sekarang. Mungkin akan ada penyimpangan dari teks dalam matematika. Atau mungkin para penulis akan terinspirasi oleh gagasan "teks produk harus sesuai untuk klien pembaca , " dan para pelopor akan dapat melanggar tradisi. Kemudian dalam 30-50-100 tahun kita akan memiliki buku pelajaran yang dapat dimengerti oleh sebagian besar pembaca.

Pembaruan1. Saya memasukkan foto dengan perhitungan panjang bagian kurva.

Pembaruan2. Dalam komentar sering disebutkan bahwa teks dikhususkan untuk masalah pengajaran, dan bukan untuk matematika profesional. Alasannya sederhana: sebagian besar pekerjaan "profesional" yang saya lihat dalam hal presentasi materi tidak berbeda dari buku teks. Pada saat yang sama, literatur sekolah / universitas diketahui mayoritas dalam habr, dan "profesional" menjadi persen.