Robomobiles tanpa driver mengirim pizza. Taksi tanpa sopir membawa orang. Truk tanpa pengemudi membawa muatan multi-ton. Jika kita menganalisis semua proyek spektakuler ini, kita akan sampai pada tugas-tugas khas yang berbeda, yang paling penting adalah pencarian dan optimalisasi rute. Masalah seperti itu diselesaikan dengan menggunakan
teori grafik . Topik ini tidak sederhana, itu dipelajari terutama di universitas atau, setidaknya, di kelas khusus senior. Tetapi dalam posting ini, saya akan menunjukkan cara menggunakan LEGO EV3 untuk mempelajari teori grafik yang sudah ada di sekolah menengah. Dan tanpa menjejalkan, tetapi pada level, menarik diterapkan.
 Konveyor Otomotif LAB EV3 Danny Benar-benar mengumpulkan mobil LEGO. Tapi itu tidak sedikit tentang dia.
Konveyor Otomotif LAB EV3 Danny Benar-benar mengumpulkan mobil LEGO. Tapi itu tidak sedikit tentang dia.Agar transportasi tak berawak mencapai tempat yang dibutuhkan, ia harus mampu membangun rute antara titik-titik yang diberikan. Diinginkan dan konsisten dengan aturan lalu lintas. Untuk mensimulasikan dan memecahkan masalah seperti itu, kita membutuhkan platform seluler LEGO EV3 dan, pada kenyataannya, peta tempat platform ini akan bergerak.
Platform Mobile LEGO EV3
Platform seluler kami harus dilengkapi dengan sensor dan servos. Semua yang Anda butuhkan dapat ditemukan di set pendidikan dasar LEGO Mindstorms EV3 45544. Inilah yang terlihat seperti platform:

Perakitan tidak membutuhkan pengetahuan elektronik dan tidak lebih dari setengah jam. Platform memiliki semua yang Anda butuhkan untuk naik ke tingkat abstraksi yang tinggi dalam menyelesaikan masalah.
Peta jalan
Mari kita menggambar peta jalan dalam bentuk kotak. Garis adalah jalan, titik persimpangan adalah persimpangan jalan:
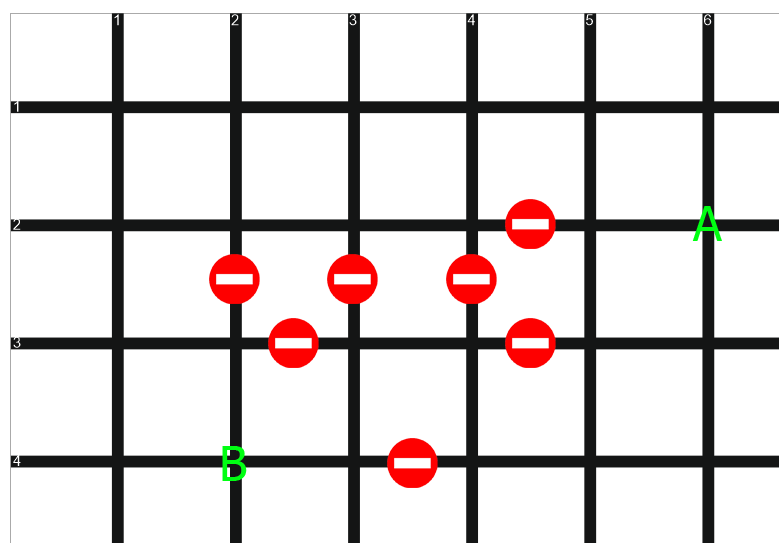
Semua bagian jalan antara persimpangan memiliki panjang yang sama, lalu lintas di sana adalah dua arah. Beberapa jalan diblokir - mereka ditandai dengan "batu bata". Selain itu, semua belokan di peta kami adalah kelipatan 90 derajat. Komplikasi grid jalan tidak akan mempengaruhi prinsip pemecahan masalah, dan untuk kejelasan, kita akan lakukan dengan opsi yang cukup sederhana. Tugas kita adalah mengemudi dari titik A ke titik B tentang jalur terpendek.
Hitung
Setiap persimpangan memiliki koordinatnya sendiri - angka garis horizontal dan vertikal. Dalam teori grafik, persimpangan seperti itu disebut
simpul . Jalan antar persimpangan ditandai dengan panah. Dalam teori grafik, ini adalah
edge . Semua jalan dua arah (panah di kedua arah) berarti grafik
tidak berorientasi . Biaya (waktu perjalanan) adalah sama untuk semua bagian jalan, yang berarti grafik tidak
berbobot .

Matriks adjacency
Grafik yang diwakili oleh gambar dengan jelas menunjukkan peta dan koneksi di dalamnya. Tetapi di komputer - termasuk EV3 - sulit untuk memproses informasi grafik. Optimal untuk menyandikan grafik dengan matriks, matriks adjacency.
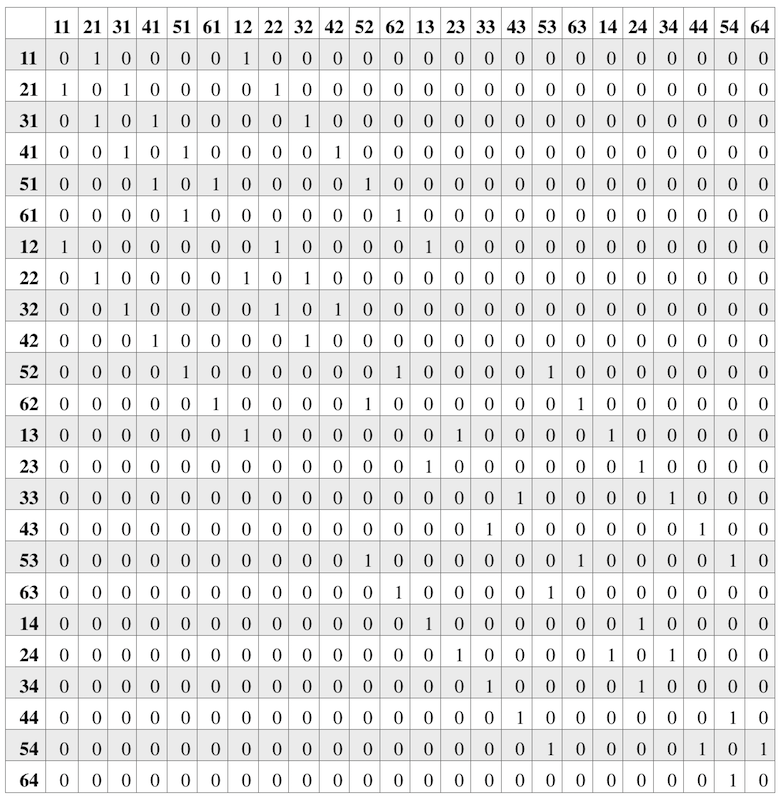
Jika tidak ada koneksi langsung antara persimpangan, kami menempatkan 0. Jika ada - 1. Jika ada - 1. Kami sepakat bahwa semua jarak antara persimpangan yang berdekatan sama dengan 1. Jika grafik ditimbang, alih-alih persatuan di setiap persimpangan kita akan meletakkan “ berat ”plot. Dan jika arah gerak diperhitungkan, maka matriks di atas akan asimetris - dalam satu arah bisa 1, dan di 0 lainnya.
Dengan matriks adjacency, robot kami sudah dapat menyelesaikan masalah - temukan jalur terpendek dari A ke B. Tetapi kami memiliki matriks dua dimensi, dan dalam EV3 hanya array satu dimensi yang dapat disimpan. Kita dapat dengan mudah pergi ke array satu dimensi melalui shift n * Y + X, di mana n adalah ukuran matriks.
Algoritma Dijkstra
Algoritma Dijkstra, algoritma untuk menemukan jalur terpendek antara satu titik grafik dan yang lainnya, akan digunakan untuk menyelesaikan. Algoritma ini ditemukan pada tahun 1956 oleh ilmuwan Belanda Edsger Dijkstroy. Jika penjelasannya sesederhana mungkin, maka algoritmanya didasarkan pada kemajuan berurutan ke simpul-simpul tetangga dari grafik dengan penilaian konstan terhadap jarak yang ditempuh. Contoh ilustrasi yang bagus dan diagram alur dasar algoritma dapat ditemukan di artikel Wikipedia.
Dalam kasus kami, diagram alur algoritma Dijkstra (“Dijkstra” kami) akan terlihat seperti ini:
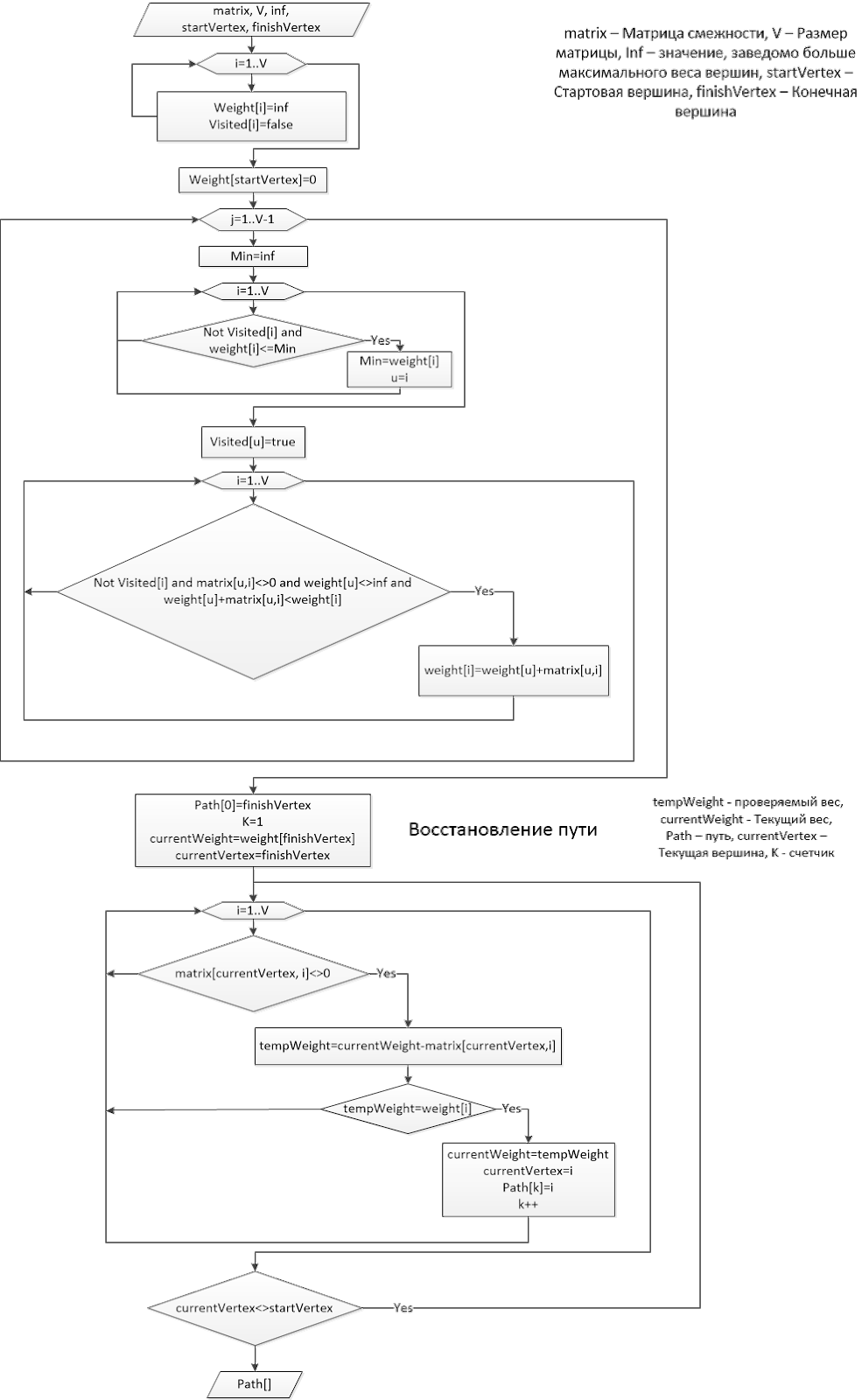
Menurut algoritma, dan lebih baik sesuai dengan model matematika, kita sudah bisa membuat program untuk robot. Input akan menjadi matriks kedekatan, titik awal dan akhir. Setelah semua tindakan yang dijelaskan, pencarian jalur terpendek antara titik-titik pada peta yang sama dapat ditemukan dengan cepat.
Tentu saja, selain algoritma Dijkstra, robot berbasis LEGO EV3 kami akan memerlukan sejumlah modul program yang lebih sederhana (subprogram): bergerak di sepanjang garis ke persimpangan, menghitung persimpangan, berbelok ke dua arah, menentukan lokasi Anda relatif terhadap sistem koordinat absolut X, Y, where, di mana X, Y - koordinat pada grid, Θ - arah robot saat ini (dinyatakan melalui kode, misalnya 1 - atas, 2 - ke kanan, 3 - bawah, 4 - ke kiri).
Dan di sini adalah demonstrasi langsung dari solusi untuk masalah tersebut. Input data sedikit berbeda, tetapi ini tidak mengubah esensi.Tema bonus: odometri
Kemampuan Odometry dapat diintegrasikan ke dalam tugas-tugas untuk bergerak di tanah - misalnya, sehingga robot di labirin mengerti di mana ia berada dan di mana ia bergerak. Menggunakan odometry, pergerakan robot diperkirakan berdasarkan data tentang pergerakan drive (rotasi motor). Mengetahui diameter roda, kita dapat menghitung jarak yang ditempuh robot dalam waktu tertentu. Mengetahui kecepatan sudut roda, kita dapat menentukan sudut dimana robot berubah relatif terhadap aslinya. Dan dengan mengatur kecepatan sudut yang berbeda, kita dapat menyesuaikan pergerakan robot di sepanjang busur dan pada saat yang sama menentukan "loop" saat memindahkan robot, seperti dalam video di bawah ini:
Di sekolah-sekolah, banyak perhatian diberikan pada trigonometri, tetapi aplikasi praktisnya tidak dicakup dengan cara apa pun. Masalah odometri yang diselesaikan dengan LEGO EV3 menunjukkan mengapa trigonometri mungkin diperlukan sama sekali. Dalam praktiknya, odometri tidak hanya digunakan dalam transportasi, tetapi juga, misalnya, untuk melacak posisi alat di mesin CNC (kontrol numerik).
Di mana saya bisa belajar semua ini?
Saya mengizinkan beberapa iklan untuk diri saya sendiri. Tugas yang dijelaskan di atas, dan tugas yang lebih kompleks mungkin diselesaikan oleh anak-anak kelas 7-9 yang telah dilatih di klub robotika. Saya menjalankan satu klub seperti itu, Robit, di Yekaterinburg - ini adalah
program pelatihan kami. Kami merekam video dari demo untuk tugas di atas di salah satu kelas. Kemudian siswa kelas delapan dari klub kami dalam 6 jam mempelajari dasar-dasar teori grafik dan memecahkan masalah yang sama.
Bagaimana memilih lingkungan pemrograman LEGO EV3
Penyelesaian masalah tidak mungkin dilakukan tanpa memilih lingkungan pemrograman yang tepat untuk LEGO EV3. Ada
materi terpisah tentang yang terbaru di area ini. Saya mencoba mengajar anak-anak untuk memilih bahasa pemrograman untuk tugas itu, dan bukan tugas untuk bahasa pemrograman itu, sintaks yang mereka pelajari. Tetapi di kelas bawah sulit untuk segera bekerja dalam bahasa pemrograman berbasis teks, jadi kami mulai mempelajari algoritma dalam bahasa grafis, di mana ambang entri lebih rendah. Dari 10 tahun, siswa belajar lingkungan grafis dari Mindstorms EV3. Beberapa kompetisi robotika membatasi hanya toolkit untuk lingkungan ini.
Sejak usia 12 tahun, mereka mulai menguasai lingkungan Dasar EV3. Lingkungan relatif mudah dipelajari, dan Basic menawarkan fungsionalitas yang kuat untuk platform LEGO EV3. Selain itu, kami memprogram di lingkungan EV3Dev, tempat Anda dapat menginstal banyak bahasa berbeda - Python, Java, C. Dengan EV3Dev, mereka mendapatkan pengalaman pertama dalam bahasa populer yang sedang populer. Satu-satunya minus dari EV3Dev adalah tingkat polling sensor yang relatif lebih rendah dibandingkan dengan lingkungan lain. Dengan pendekatan yang tepat, LEGO EV3 menjadi alat yang hebat untuk mengenal pemrograman. Ketika siswa melihat kode mereka meniupkan kehidupan ke dalam sebuah konstruktor, ini adalah motivasi yang sangat baik.
Apa selanjutnya
Setelah mempelajari algoritme semacam itu di sekolah menengah, anak-anak akan dapat lebih mengkonsolidasikan pengetahuan mereka dan, misalnya, berpartisipasi dalam Olimpiade desain dan mata pelajaran yang memberikan bonus nyata - misalnya, 100 poin secara otomatis pada ujian saat memasuki universitas.