Siswa mengenal masalah beltway dengan mengambil kursus bioinformatika, khususnya, salah satu kualitas tertinggi dan semangat terdekat untuk programmer adalah program Bioinformatika (Pavel Pevzner) pada coursera dari University of California San Diego. Masalahnya menarik perhatian oleh kesederhanaan pernyataan, kepentingan praktis, dan oleh fakta bahwa itu masih dianggap belum terpecahkan dengan kemampuan nyata untuk menyelesaikannya dengan pengkodean sederhana. Masalahnya ditimbulkan dengan cara ini. Apakah mungkin untuk mengembalikan koordinat banyak titik
dalam waktu polinomial $ inline $ X $ inline $ jika himpunan semua jarak berpasangan di antara keduanya diketahui
$ inline $ \ Delta X $ inline $ ?
Tugas yang tampaknya sederhana ini masih ada dalam daftar masalah geometri komputasi yang belum terpecahkan. Selain itu, situasinya bahkan tidak menyangkut titik-titik dalam ruang multidimensi, terutama yang melengkung, masalahnya sudah merupakan pilihan paling sederhana - ketika semua titik memiliki koordinat bilangan bulat dan terlokalisasi pada garis yang sama.
Dalam hampir setengah abad terakhir sejak tugas ini diakui oleh ahli matematika sebagai tantangan (Shamos, 1975), beberapa hasil diperoleh. Kami mempertimbangkan dua kasus yang mungkin untuk masalah satu dimensi:
- poin terletak pada garis lurus (masalah turnpike)
- poin terletak pada lingkaran (masalah beltway)
Dua kasus ini menerima nama yang berbeda karena suatu alasan - dibutuhkan upaya yang berbeda untuk menyelesaikannya. Memang, tugas pertama diselesaikan dengan cukup cepat (dalam 15 tahun) dan algoritma backtracking dibangun, yang mengembalikan solusi rata-rata dalam waktu kuadratik
$ inline $ O (n ^ 2 \ log n) $ inline $ dimana
$ inline $ n $ inline $ - jumlah poin (Skiena, 1990); untuk tugas kedua ini belum dilakukan sejauh ini, dan algoritma yang diusulkan terbaik memiliki kompleksitas komputasi eksponensial
$ inline $ O (n ^ n \ log n) $ inline $ (Lemke, 2003). Gambar di bawah ini menunjukkan perkiraan berapa lama komputer Anda akan bekerja untuk mendapatkan solusi untuk satu set dengan jumlah poin yang berbeda.

Artinya, dalam waktu yang dapat diterima secara psikologis (~ 10 detik), Anda dapat memulihkan banyak
$ inline $ X $ inline $ hingga 10 ribu poin dalam case turnpike dan hanya ~ 10 poin untuk case beltway, yang sama sekali tidak berharga untuk aplikasi praktis.
Sedikit klarifikasi. Dipercayai bahwa masalah turnpike diselesaikan dalam hal penggunaan praktis, yaitu, untuk sebagian besar data yang ditemukan. Dalam kasus ini, keberatan matematikawan murni terhadap fakta bahwa ada set data khusus yang waktu untuk mendapatkan solusi secara eksponensial diabaikan
$ inline $ O (2 ^ n \ log n) $ inline $ (Zhang, 1982). Berbeda dengan turnpike, masalah beltway dengan algoritma eksponensial tidak dapat dianggap diselesaikan dengan cara apa pun.
Pentingnya memecahkan masalah beltway dalam hal bioinformatika
Pada akhir abad ke-20, sebuah jalur baru untuk sintesis biomolekul, yang disebut jalur sintesis nonribosom, ditemukan. Perbedaan utamanya dari jalur sintesis klasik adalah bahwa hasil sintesis akhir tidak dikodekan menjadi DNA sama sekali. Sebaliknya, hanya kode "alat" (banyak sintetase berbeda) yang dapat mengumpulkan benda-benda ini yang ditulis ke dalam DNA. Dengan demikian, rekayasa biomachine diperkaya secara signifikan, dan alih-alih satu jenis kolektor tunggal (ribosom), yang bekerja hanya dengan 20 bagian standar (asam amino standar, juga disebut proteinogenik), banyak jenis kolektor lain yang dapat bekerja dengan lebih dari 500 bagian standar dan non-standar. (Asam amino non-proteinogenik dan berbagai modifikasinya). Dan perakit ini tidak hanya dapat menghubungkan bagian-bagian ke dalam rantai, tetapi juga mendapatkan struktur yang sangat rumit - siklik, bercabang, serta struktur dengan banyak siklus dan percabangan. Semua ini secara signifikan meningkatkan gudang sel untuk berbagai kasus kehidupannya. Aktivitas biologis struktur semacam itu tinggi, spesifisitas (selektivitas aksi), juga, berbagai sifat tidak terbatas. Kelas produk sel ini dalam literatur bahasa Inggris disebut NRP (produk non-ribosom, atau peptida non-ribosom). Ahli biologi berharap bahwa justru di antara produk metabolisme sel inilah sediaan farmakologis baru dapat ditemukan yang sangat efektif dan tidak memiliki efek samping karena kekhususan.
Satu-satunya pertanyaan adalah, bagaimana dan di mana mencari NRP? Mereka sangat efektif, oleh karena itu sel sama sekali tidak perlu memproduksinya dalam jumlah besar, dan konsentrasinya dapat diabaikan. Jadi metode ekstraksi kimia dengan akurasi rendah ~ 1% dan reagen besar dan biaya waktu tidak berguna. Selanjutnya Mereka tidak dikodekan dalam DNA, yang berarti bahwa semua database yang terakumulasi selama decoding genom, dan semua metode bioinformatika dan genomik, juga tidak berguna. Satu-satunya cara untuk menemukan sesuatu adalah melalui metode fisik, yaitu spektroskopi massa. Selain itu, tingkat deteksi zat dalam spektrometer modern sangat tinggi sehingga memungkinkan seseorang untuk menemukan jumlah yang tidak signifikan, dalam total> ~ 800 molekul (rentang atto-molar, atau konsentrasi
$ inline $ 10 ^ {- 18} $ inline $ )
"
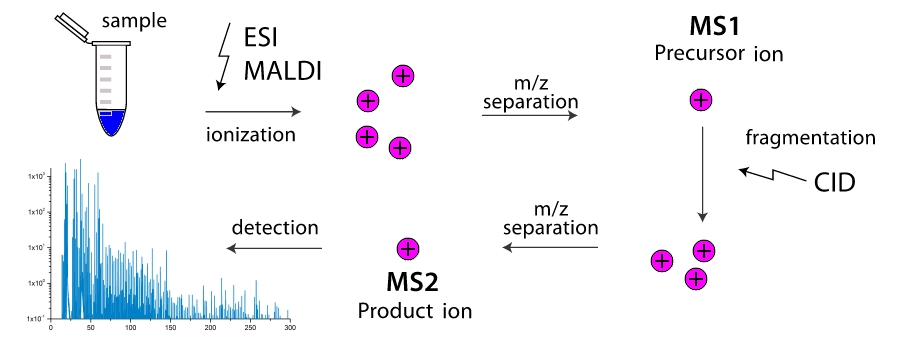
Bagaimana cara kerja spektrometer massa? Di ruang kerja perangkat, molekul dipecah menjadi fragmen (lebih sering melalui tabrakan mereka satu sama lain, lebih jarang karena pengaruh eksternal). Fragmen-fragmen ini terionisasi, dan kemudian dipercepat dan dipisahkan dalam medan elektromagnetik eksternal. Pemisahan terjadi baik pada saat detektor mencapai, atau dengan sudut putaran medan magnet, karena massa fragmen lebih besar dan muatannya lebih rendah, semakin canggung itu. Jadi, spektrometer massa “menimbang” massa fragmen. Selain itu, "penimbangan" dapat dilakukan secara bertahap, dengan berulang kali memfilter fragmen dengan massa yang sama (lebih tepatnya, dengan satu nilai
$ inline $ m / z $ inline $ ) dan mendorong mereka melalui fragmentasi dengan pemisahan lebih lanjut. Spektrometer massa dua tahap didistribusikan secara luas dan disebut spektrometer massa tandem, spektrometer massa multi-tahap sangat jarang, dan hanya ditunjuk sebagai
$ inline $ ms ^ n $ inline $ dimana
$ inline $ n $ inline $ - jumlah tahapan. Dan di sini tugas muncul, bagaimana, hanya mengetahui massa dari semua jenis fragmen dari molekul mana pun, untuk mengetahui strukturnya? Jadi kami sampai pada masalah turnpike dan beltway, masing-masing untuk peptida linier dan siklik.
Saya akan menjelaskan secara lebih rinci bagaimana tugas memulihkan struktur biomolekul dikurangi menjadi masalah yang ditunjukkan dengan menggunakan contoh peptida siklik.
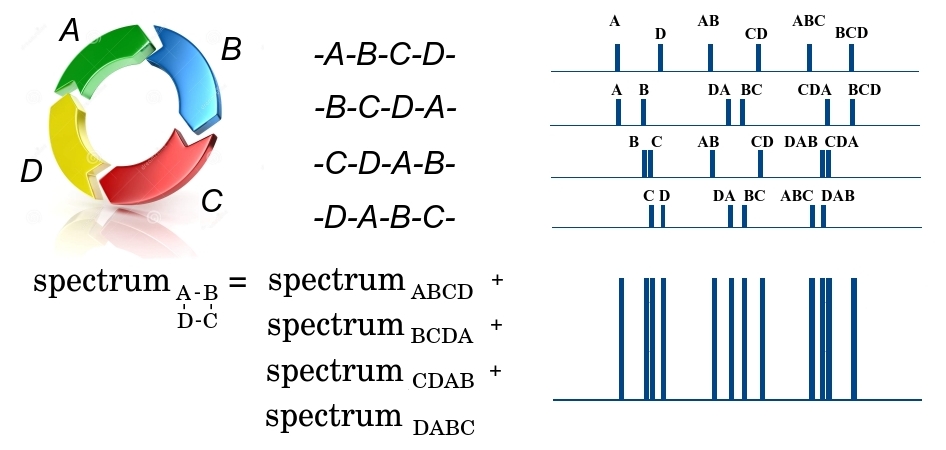
ABCD peptida siklik pada tahap pertama fragmentasi dapat dipecah di 4 tempat, baik dengan hubungan DA, atau oleh AB, BC atau CD, membentuk 4 peptida linier yang memungkinkan - baik ABCD, BCDA, CDAB atau DABC. Karena sejumlah besar peptida identik melewati spektrometer, kita akan memiliki fragmen dari keempat jenis pada output. Selain itu, kami mencatat bahwa semua fragmen memiliki massa yang sama, dan tidak dapat dipisahkan pada tahap pertama. Pada tahap kedua, ABCD fragmen linier dapat dipecah di tiga tempat, membentuk fragmen yang lebih kecil dengan massa A dan BCD yang berbeda, AB dan CD, ABC dan D, dan membentuk spektrum massa yang sesuai. Dalam spektrum ini, massa fragmen diplot sepanjang sumbu x, dan jumlah fragmen kecil dengan massa yang diberikan sepanjang sumbu y. Demikian pula, spektrum dibentuk untuk tiga fragmen linier sisa BCDA, CDAB, dan DABC. Karena semua 4 fragmen besar diteruskan ke tahap kedua, semua spektrumnya ditambahkan. Total, hasilnya beberapa massa
$ inline $ \ {m_1 ^ {n_1}, m_2 ^ {n_2}, .., m_q ^ {n_q} \} $ inline $ dimana
$ inline $ m_i $ inline $ - beberapa massa, dan
$ inline $ n_i $ inline $ - frekuensi pengulangannya. Pada saat yang sama, kita tidak tahu fragmen mana yang dimiliki massa ini dan apakah fragmen ini unik, karena fragmen yang berbeda dapat memiliki satu massa. Semakin jauh ikatan dalam peptida berasal dari satu sama lain, semakin besar massa fragmen peptida di antara mereka. Yaitu, tugas mengembalikan urutan elemen dalam peptida siklik berkurang menjadi masalah beltway, di mana elemen-elemen set
$ inline $ X $ inline $ adalah ikatan dalam peptida, dan elemen banyak
$ inline $ \ Delta X $ inline $ - massa fragmen di antara ikatan.
Antisipasi adanya algoritma dengan waktu polinomial untuk menyelesaikan masalah beltway
Dari pengalaman saya sendiri dan dari berkomunikasi dengan orang-orang yang mencoba atau benar-benar melakukan sesuatu untuk menyelesaikan masalah ini, saya perhatikan bahwa sebagian besar orang mencoba menyelesaikannya baik dalam kasus umum atau untuk data integer dalam kisaran sempit, seperti ini (1, 50). Kedua opsi ini akan gagal. Untuk kasus umum, terbukti bahwa jumlah total solusi untuk masalah beltway dalam kasus satu dimensi
$ inline $ S_1 (n) $ inline $ dibatasi oleh nilai-nilai (Lemke, 2003)
$$ menampilkan $$ e ^ {2 ^ {\ frac {\ ln n} {\ ln \ ln n} + o (1)}} \ leq S_1 (n) \ leq \ frac {1} {2} n ^ {n-2} $$ tampilkan $$
yang berarti adanya sejumlah solusi eksponensial dalam asimptotik
$ inline $ n \ rightarrow \ infty $ inline $ . Jelas, jika jumlah solusi tumbuh secara eksponensial, maka waktu penerimaan mereka tidak dapat tumbuh lebih lambat. Artinya, untuk kasus umum, tidak mungkin mendapatkan solusi waktu polinomial. Adapun data integer dalam kisaran sempit, semuanya dapat diverifikasi secara eksperimental, karena tidak terlalu sulit untuk menulis kode yang mencari solusi dengan pencarian lengkap. Untuk kecil
$ inline $ n $ inline $ kode seperti itu tidak akan memakan waktu lama. Hasil pengujian kode semacam itu akan menunjukkan bahwa dalam kondisi data seperti itu, jumlah total solusi yang berbeda untuk perangkat apa pun
$ inline $ \ Delta X $ inline $ sudah kecil
$ inline $ n $ inline $ juga tumbuh sangat tajam.
Setelah mempelajari fakta-fakta ini, Anda dapat menyerah dan menyerah pada tugas ini. Saya akui bahwa inilah salah satu alasan mengapa masalah beltway masih dianggap belum terselesaikan. Namun, celah memang ada. Ingatlah bahwa fungsi eksponensial
$ inline $ e ^ {\ alpha x} $ inline $ berperilaku sangat menarik. Pada awalnya, itu tumbuh sangat lambat, naik dari 0 ke 1 selama interval yang jauh lebih besar dari
$ inline $ \ infty $ inline $ ke 0, maka pertumbuhannya semakin cepat. Namun, semakin rendah nilainya
$ inline $ \ alpha $ inline $ semakin besar nilainya
$ inline $ x $ inline $ sehingga hasil dari langkah fungsi lebih dari beberapa nilai yang ditetapkan
$ inline $ y = \ xi $ inline $ . Sebagai nilai seperti itu, akan lebih mudah untuk memilih nomor
$ inline $ \ xi = 2 $ inline $ , sebelum dia satu-satunya solusi, setelah dia ada banyak keputusan. Pertanyaan Dan apakah ada yang memeriksa ketergantungan pada jumlah keputusan pada data apa yang didapat pada input? Ya saya lakukan. Ada disertasi PhD yang luar biasa oleh matematikawan wanita Kroasia Tamara Dakis (Dakic, 2000), di mana ia menentukan kondisi apa yang harus dipenuhi oleh data input agar masalah dapat diselesaikan dalam waktu polinomial. Yang paling penting dari mereka adalah keunikan solusi dan tidak adanya duplikasi dalam set input data.
$ inline $ \ Delta X $ inline $ . Tingkat disertasinya sangat tinggi. Sangat disayangkan bahwa siswa ini membatasi dirinya hanya untuk masalah belokan, saya yakin bahwa jika dia mengalihkan minatnya pada masalah beltway, itu sudah lama terselesaikan.
Memperoleh suatu algoritma dengan waktu pemecahan masalah polinomial
Itu mungkin untuk menemukan data yang memungkinkan untuk membangun algoritma yang diinginkan secara kebetulan. Butuh gagasan tambahan. Gagasan utama muncul dari pengamatan (lihat di atas) bahwa spektrum peptida siklik adalah jumlah dari spektrum semua peptida linier yang terbentuk pada satu ring break. Karena urutan asam amino dalam peptida dapat dipulihkan dari peptida linier semacam itu, jumlah total garis dalam spektrum adalah signifikan (dalam
$ inline $ n $ inline $ saat di mana
$ inline $ n $ inline $ - jumlah asam amino dalam peptida) berlebihan. Pertanyaannya hanya garis mana yang harus dikeluarkan dari spektrum agar tidak kehilangan kemampuan untuk mengembalikan urutan. Karena kedua tugas (pemulihan urutan peptida siklik dari spektrum massa dan masalah beltway) secara matematis isomorfik, juga dimungkinkan untuk menipiskan banyak
$ inline $ \ Delta X $ inline $ .
Operasi penipisan
$ inline $ \ Delta X $ inline $ dibangun menggunakan simetri lokal set
$ inline $ \ Delta X $ inline $ (Fomin, 2016a).
- Symmetrization Operasi pertama adalah memilih elemen sewenang-wenang dari set $ inline $ x _ {\ mu} \ in \ Delta X $ inline $ dan hapus dari $ inline $ \ Delta X $ inline $ semua elemen kecuali yang memiliki pasangan simetris sehubungan dengan poin $ inline $ x _ {\ mu} / 2 $ inline $ dan $ inline $ (L + x _ {\ mu}) / 2 $ inline $ dimana $ inline $ L $ inline $ - lingkar (Saya ingat bahwa dalam kasus beltway, semua titik terletak pada lingkaran).
- Konvolusi solusi parsial. Operasi kedua menggunakan dugaan tentang solusi, yaitu, pengetahuan tentang poin individu yang termasuk dalam solusi, yang disebut solusi parsial. Dari banyak $ inline $ \ Delta X $ inline $ semua elemen juga dihapus, kecuali yang memenuhi syarat - jika kita mengukur jarak dari titik yang diuji ke semua titik solusi parsial, maka semua nilai yang diperoleh berada dalam $ inline $ \ Delta X $ inline $ . Saya akan mengklarifikasi bahwa jika setidaknya satu dari jarak yang diperoleh tidak ada $ inline $ \ Delta X $ inline $ maka intinya diabaikan.
Teorema terbukti bahwa kedua operasi menipiskan set
$ inline $ \ Delta X $ inline $ , tetapi masih memiliki cukup elemen untuk memulihkan solusi
$ inline $ X $ inline $ . Menggunakan operasi ini, sebuah algoritma dibangun dan diimplementasikan dalam c ++ untuk menyelesaikan masalah beltway (Fomin, 2016b). Algoritma sedikit berbeda dari algoritma backtracking klasik (yaitu, kami mencoba membangun solusi dengan menghitung opsi yang mungkin dan kembali jika kami mendapatkan kesalahan selama konstruksi). Satu-satunya perbedaan adalah untuk mempersempit set
$ inline $ \ Delta X $ inline $ untuk menguji kita menjadi opsi yang jauh lebih sedikit.
Ini contoh berapa banyak
$ inline $ \ Delta X $ inline $ saat menipis.

Percobaan komputasi dilakukan untuk peptida siklik yang dihasilkan secara panjang
$ inline $ n $ inline $ dari 10 hingga 1000 asam amino (sumbu ordinat pada skala logaritmik). Absis juga menunjukkan pada skala logaritmik jumlah elemen dalam set menipis oleh berbagai operasi
$ inline $ \ Delta X $ inline $ dalam satuan
$ inline $ n $ inline $ . Representasi seperti itu sama sekali tidak biasa, oleh karena itu saya akan menguraikan bagaimana itu dibaca pada contoh. Kami melihat diagram kiri. Biarkan peptida memiliki panjang
$ inline $ n = 100 $ inline $ . Baginya, jumlah elemen di set
$ inline $ \ Delta X $ inline $ sama dengan
$ inline $ n ^ 2 = $ 10.000 inline $ (Ini adalah titik di garis putus-putus atas
$ inline $ y = n ^ 2 $ inline $ ) Setelah menghapus dari set
$ inline $ \ Delta X $ inline $ elemen berulang, jumlah elemen dalam
$ inline $ \ Delta X $ inline $ berkurang menjadi
$ inline $ n_D \ approx n ^ {1.9} \ sekitar 6300 $ inline $ (lingkaran dengan tanda silang). Setelah simetriisasi, jumlah elemen turun menjadi
$ inline $ n_S \ approx n ^ {1.75} \ sekitar 3100 $ inline $ (lingkaran hitam), dan setelah konvolusi dengan solusi parsial untuk
$ inline $ n_C \ approx n ^ {1.35} \ sekitar 500 $ inline $ (silang). Total, total volume set
$ inline $ \ Delta X $ inline $ berkurang hanya 20 kali. Untuk peptida dengan panjang yang sama, tetapi dalam diagram kanan, kontraksi berasal
$ inline $ n ^ 2 = $ 10.000 inline $ sebelumnya
$ inline $ N_C \ approx n \ sekitar 100 $ inline $ 100 kali.
Perhatikan bahwa generasi kasus uji untuk diagram kiri dilakukan sehingga tingkat duplikasi
$ inline $ k_ {dup} $ inline $ masuk
$ inline $ \ Delta X $ inline $ berada di kisaran 0,1 hingga 0,3, dan untuk kanan - kurang dari 0,1. Tingkat duplikasi didefinisikan sebagai
$ inline $ k_ {dup} = 2- \ log {N_u} / \ log {n} $ inline $ dimana
$ inline $ N_u $ inline $ - jumlah elemen unik di set
$ inline $ \ Delta X $ inline $ . Definisi semacam itu memberikan hasil alami: dengan tidak adanya duplikat di set
$ inline $ \ Delta X $ inline $ kekuatannya sama
$ inline $ N_u = n ^ 2 $ inline $ dan
$ inline $ k_ {dup} = 0 $ inline $ duplikasi maksimum yang mungkin
$ inline $ N_u = n $ inline $ dan
$ inline $ k_ {dup} = 1 $ inline $ . Bagaimana memungkinkan untuk memberikan tingkat duplikasi yang berbeda, saya akan katakan sedikit kemudian. Diagram menunjukkan bahwa semakin rendah tingkat duplikasi, semakin tipis
$ inline $ \ Delta X $ inline $ di
$ inline $ k_ {dup} <0,1 $ inline $ jumlah elemen dalam menipis
$ inline $ \ Delta X $ inline $ umumnya mencapai batasnya
$ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ , karena dalam set dihancurkan kurang dari
$ inline $ O (n) $ inline $ elemen tidak dapat diperoleh (operasi menyimpan elemen yang cukup untuk mendapatkan solusi
$ inline $ n $ inline $ elemen). Fakta mempersempit kekuatan set
$ inline $ \ Delta X $ inline $ ke batas bawah sangat penting, dialah yang menyebabkan perubahan dramatis dalam kompleksitas komputasi untuk mendapatkan solusi.
Setelah memasukkan operasi penjarangan dalam algoritma backtracking dan dalam memecahkan masalah beltway, analog lengkap dari apa yang Tamara Dakis bicarakan tentang masalah turnpike terungkap. Biarkan saya mengingatkan Anda. Dia mengatakan bahwa untuk masalah turnpike adalah mungkin untuk mendapatkan solusi dalam waktu polinomial jika solusinya unik dan tidak ada duplikasi dalam
$ inline $ \ Delta X $ inline $ . Ternyata tidak adanya duplikasi sama sekali tidak perlu (hampir tidak mungkin untuk data nyata), cukup bahwa levelnya akan sangat kecil. Gambar di bawah ini menunjukkan berapa banyak waktu yang diperlukan untuk mendapatkan solusi dari masalah beltway tergantung pada panjang peptida dan tingkat duplikasi dalam
$ inline $ \ Delta X $ inline $ .

Dalam gambar, absis dan ordinat diberikan pada skala logaritmik. Ini memungkinkan Anda untuk melihat dengan jelas apakah ketergantungan waktu penghitungan pada panjang urutan
$ inline $ T = f (n) $ inline $ eksponensial (garis lurus) atau polinomial (kurva bentuk log). Seperti dapat dilihat pada diagram, dengan tingkat duplikasi yang rendah (diagram kanan), solusinya diperoleh dalam waktu polinomial. Nah, untuk lebih tepatnya, solusinya didapat dalam waktu kuadratik. Ini terjadi ketika operasi penjarangan mengurangi daya set ke batas bawah.
$ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ , ada beberapa poin yang tersisa di dalamnya, kembali ketika menghitung pilihan menjadi tunggal, dan pada dasarnya algoritma berhenti beralih pada pilihan, tetapi hanya membangun solusi dari apa yang tersisa.
NB Nah, saya akan mengungkapkan rahasia terakhir mengenai pembuatan set pada tingkat duplikasi yang berbeda. Ini disebabkan oleh perbedaan akurasi penyajian data. Jika data dihasilkan dengan akurasi rendah (misalnya, pembulatan ke bilangan bulat), maka tingkat duplikasi menjadi tinggi, lebih dari 0,3.
Jika data dihasilkan dengan akurasi yang baik, misalnya, hingga 3 tempat desimal, maka tingkat duplikasi menurun tajam, kurang dari 0,1. Dan dari sini mengikuti komentar paling penting terakhir.Untuk data nyata, dalam kondisi akurasi pengukuran yang terus meningkat, masalah beltway menjadi dapat dipecahkan secara real time.
Sastra1. Dakic, T. (2000). Pada Masalah Turnpike. Tesis PhD, Universitas Simon Fraser.2. Fomin. E. (2016a) Pendekatan Sederhana untuk Rekonstruksi Satu Set Poin dari Multiset dari n ^ 2 Jarak Berpasangan dalam n ^ 2 Langkah untuk Urutan Masalah: I. Teori. J Comput Biol. 2016, 23 (9): 769-75.3. Fomin. E. (2016b) Pendekatan Sederhana untuk Rekonstruksi Satu Set Poin dari Multiset dari n ^ 2 Jarak Berpasangan dalam n ^ 2 Langkah untuk Urutan Masalah: II. Algoritma. J Comput Biol. 2016, 23 (12): 934-942.4. Lemke, P., Skiena, S., dan Smith, W. (2003). Merekonstruksi Set Dari Jarak Interpoint. Algoritma dan Kombinatorik Geometri Diskrit dan Komputasi, 25: 597–631.5. Skiena, S., Smith, W., dan Lemke, P. (1990). Merekonstruksi set dari jarak titik. Dalam Prosiding Simposium ACM Keenam tentang Geometri Komputasi, halaman 332-339. Berkeley, CA6. Zhang, Z. 1982. Contoh eksponensial untuk algoritma pemetaan digest sebagian. J. Comp. Biol. 1, 235–240.