Implementasi algoritma k-means (k-means) menggunakan contoh bekerja dengan piksel

Halo semuanya! Baru-baru ini, perlu untuk menulis kode untuk mengimplementasikan segmentasi gambar menggunakan metode k-means (Bahasa Inggris k-means). Nah, hal pertama yang dilakukan Google adalah bantuan. Saya menemukan banyak informasi, seperti dari sudut pandang matematika (semua jenis coretan matematika kompleks di sana, Anda akan mengerti apa yang tertulis di sana), serta beberapa implementasi perangkat lunak yang ada di Internet Inggris. Kode-kode ini tentu saja indah - tidak diragukan lagi, tetapi esensi dari gagasan ini sulit ditangkap. Entah bagaimana semuanya rumit di sana, bingung, namun, dengan tangan, dengan tangan, Anda tidak akan menulis kode, Anda tidak akan mengerti apa pun. Pada artikel ini saya ingin menunjukkan implementasi yang sederhana, tidak produktif, tetapi, saya harap, dapat dimengerti dari algoritma yang luar biasa ini. Oke, ayo pergi!

Jadi, apa pengelompokan dalam hal persepsi kita? Biarkan saya memberi Anda sebuah contoh, katakanlah ada gambar yang bagus dengan bunga-bunga dari pondok nenek Anda.



Pertanyaannya adalah: untuk menentukan berapa banyak area dalam foto ini yang diisi kira-kira dengan warna yang sama. Yah, sama sekali tidak sulit: kelopak putih - satu, pusat kuning - dua (saya bukan ahli biologi, saya tidak tahu apa namanya), tiga hijau. Bagian ini disebut cluster. Cluster adalah kombinasi data yang memiliki fitur umum (warna, posisi, dll.). Proses penentuan dan penempatan setiap komponen data apa pun dalam kelompok - bagian tersebut disebut pengelompokan.

Ada banyak algoritma pengelompokan, tetapi yang paling sederhana adalah k - medium, yang akan dibahas kemudian. K-means adalah algoritma sederhana dan efisien yang mudah diimplementasikan menggunakan metode perangkat lunak. Data yang akan kami distribusikan dalam kelompok adalah piksel. Seperti yang Anda ketahui, piksel warna memiliki tiga komponen - merah, hijau dan biru. Pengenaan komponen ini dan menciptakan palet warna yang ada.



Dalam memori komputer, setiap komponen warna ditandai oleh angka dari 0 hingga 255. Artinya, menggabungkan nilai yang berbeda dari merah, hijau dan biru, kita mendapatkan palet warna di layar.

Menggunakan piksel sebagai contoh, kami menerapkan algoritma kami. K-means adalah algoritma iteratif, yaitu, ia akan memberikan hasil yang benar, setelah sejumlah pengulangan beberapa perhitungan matematika.

Algoritma

1. Anda harus tahu sebelumnya berapa banyak cluster yang Anda butuhkan untuk mendistribusikan data. Ini adalah kelemahan yang signifikan dari metode ini, tetapi masalah ini diselesaikan dengan peningkatan implementasi algoritma, tetapi ini, seperti yang mereka katakan, adalah cerita yang sama sekali berbeda.
2. Kita perlu memilih pusat awal dari kelompok kita. Bagaimana? Ya secara acak. Mengapa Sehingga Anda dapat mengambil setiap piksel ke tengah-tengah kluster. Pusatnya seperti Raja, di mana subyeknya dikumpulkan - piksel. Ini adalah "jarak" dari pusat ke piksel yang menentukan kepada siapa setiap piksel akan mematuhinya.
3. Kami menghitung jarak dari setiap pusat ke setiap piksel. Jarak ini dianggap sebagai jarak Euclidean antara titik-titik dalam ruang, dan dalam kasus kami, sebagai jarak antara tiga komponen warna:

   $$$$ menampilkan $$ \ sqrt {(R_ {2} -R_ {1}) ^ 2 + (G_ {2} -G_ {1}) ^ 2 + (B_ {2} -B_ {1}) ^ 2} . $$ menampilkan $$

   Kami menghitung jarak dari piksel pertama ke setiap pusat dan menentukan jarak terkecil antara piksel ini dan pusat. Untuk pusat, jarak ke yang terkecil, kami menghitung ulang koordinat sebagai rata-rata aritmatika antara setiap komponen piksel - raja dan piksel - subjek. Pusat kami bergeser dalam ruang sesuai dengan perhitungan.
4. Setelah menghitung ulang semua pusat, kami mendistribusikan piksel ke dalam kelompok, membandingkan jarak dari setiap piksel ke pusat. Sebuah piksel ditempatkan dalam sebuah cluster, ke pusat yang lebih dekat daripada pusat-pusat lainnya.
5. Semuanya dimulai lagi, selama piksel tetap berada di kelompok yang sama. Seringkali ini mungkin tidak terjadi, karena dengan sejumlah besar data pusat akan bergerak dalam radius kecil, dan piksel di sepanjang tepi cluster akan melompat ke satu atau cluster lain. Untuk melakukan ini, tentukan jumlah iterasi maksimum.

Implementasi

Saya akan mengimplementasikan proyek ini dalam C ++. File pertama adalah "k_means.h", di dalamnya saya mendefinisikan tipe data utama, konstanta, dan kelas utama untuk bekerja - "K_means".
Untuk mengkarakterisasi setiap piksel, buat struktur yang terdiri dari tiga komponen piksel, untuk itu saya memilih tipe ganda untuk perhitungan yang lebih akurat, dan juga menentukan beberapa konstanta agar program dapat bekerja:

const int KK = 10; //  const int max_iterations = 100; //   typedef struct { double r; double g; double b; } rgb; 

K_means kelas itu sendiri:

 class K_means { private: std::vector<rgb> pixcel; int q_klaster; int k_pixcel; std::vector<rgb> centr; void identify_centers(); inline double compute(rgb k1, rgb k2) { return sqrt(pow((k1.r - k2.r),2) + pow((k1.g - k2.g), 2) + pow((k1.b - k2.b), 2)); } inline double compute_s(double a, double b) { return (a + b) / 2; }; public: K_means() : q_klaster(0), k_pixcel(0) {}; K_means(int n, rgb *mas, int n_klaster); K_means(int n_klaster, std::istream & os); void clustering(std::ostream & os); void print()const; ~K_means(); friend std::ostream & operator<<(std::ostream & os, const K_means & k); }; 

Mari kita bahas komponen-komponen kelas:

vectorpixcel - vektor untuk piksel;
q_klaster - jumlah cluster;
k_pixcel - jumlah piksel;
vectorcentr - vektor untuk pusat pengelompokan, jumlah elemen di dalamnya ditentukan oleh q_klaster;
ident_centers () - metode untuk memilih pusat awal secara acak di antara piksel input;
compute () dan compute_s () adalah metode bawaan untuk menghitung jarak antara piksel dan pusat penghitungan ulang, masing-masing;
tiga konstruktor: yang pertama adalah secara default, yang kedua adalah untuk menginisialisasi piksel dari sebuah array, yang ketiga adalah untuk menginisialisasi piksel dari file teks (dalam implementasi saya, file secara tidak sengaja diisi dengan data pada awalnya, dan kemudian piksel dibaca dari file ini untuk program untuk bekerja, mengapa tidak langsung ke vektor - hanya dibutuhkan dalam kasus saya);
clustering (std :: ostream & os) - metode clustering;
metode dan kelebihan pernyataan output untuk mempublikasikan hasil.

Implementasi Metode:

 void K_means::identify_centers() { srand((unsigned)time(NULL)); rgb temp; rgb *mas = new rgb[q_klaster]; for (int i = 0; i < q_klaster; i++) { temp = pixcel[0 + rand() % k_pixcel]; for (int j = i; j < q_klaster; j++) { if (temp.r != mas[j].r && temp.g != mas[j].g && temp.b != mas[j].b) { mas[j] = temp; } else { i--; break; } } } for (int i = 0; i < q_klaster; i++) { centr.push_back(mas[i]); } delete []mas; } 

Ini adalah metode untuk memilih pusat pengelompokan awal dan menambahkannya ke vektor pusat. Pemeriksaan dilakukan untuk mengulangi pusat dan menggantinya dalam kasus ini.

 K_means::K_means(int n, rgb * mas, int n_klaster) { for (int i = 0; i < n; i++) { pixcel.push_back(*(mas + i)); } q_klaster = n_klaster; k_pixcel = n; identify_centers(); } 

Implementasi konstruktor untuk menginisialisasi piksel dari array.

 K_means::K_means(int n_klaster, std::istream & os) : q_klaster(n_klaster) { rgb temp; while (os >> temp.r && os >> temp.g && os >> temp.b) { pixcel.push_back(temp); } k_pixcel = pixcel.size(); identify_centers(); } 

Kami meneruskan objek input ke konstruktor ini untuk dapat memasukkan data dari file dan konsol.

 void K_means::clustering(std::ostream & os) { os << "\n\n :" << std::endl; /*             :        ,    -  ,    ,   ,        .*/ std::vector<int> check_1(k_pixcel, -1); std::vector<int> check_2(k_pixcel, -2); int iter = 0; /* .*/ while(true) { os << "\n\n----------------  №" << iter << " ----------------\n\n"; { for (int j = 0; j < k_pixcel; j++) { double *mas = new double[q_klaster]; /*  :          .      ,   .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[j], centr[i]); os << "   " << j << "   #" << i << ": " << *(mas + i) << std::endl; } /*     m_k      .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } os << "    #" << m_k << std::endl; os << "  #" << m_k << ": "; centr[m_k].r = compute_s(pixcel[j].r, centr[m_k].r); centr[m_k].g = compute_s(pixcel[j].g, centr[m_k].g); centr[m_k].b = compute_s(pixcel[j].b, centr[m_k].b); os << centr[m_k].r << " " << centr[m_k].g << " " << centr[m_k].b << std::endl; delete[] mas; } /*   .*/ int *mass = new int[k_pixcel]; os << "\n  : "<< std::endl; for (int k = 0; k < k_pixcel; k++) { double *mas = new double[q_klaster]; /*    .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[k], centr[i]); os << "   №" << k << "   #" << i << ": " << *(mas + i) << std::endl; } /*  .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } mass[k] = m_k; os << " №" << k << "     #" << m_k << std::endl; } /*            .*/ os << "\n    : \n"; for (int i = 0; i < k_pixcel; i++) { os << mass[i] << " "; check_1[i] = *(mass + i); } os << std::endl << std::endl; os << " : " << std::endl; int itr = KK + 1; for (int i = 0; i < q_klaster; i++) { os << " #" << i << std::endl; for (int j = 0; j < k_pixcel; j++) { if (mass[j] == i) { os << pixcel[j].r << " " << pixcel[j].g << " " << pixcel[j].b << std::endl; mass[j] = ++itr; } } } delete[] mass; /*    .*/ os << " : \n" ; for (int i = 0; i < q_klaster; i++) { os << centr[i].r << " " << centr[i].g << " " << centr[i].b << " - #" << i << std::endl; } } /*         –  .*/ iter++; if (check_1 == check_2 || iter >= max_iterations) { break; } check_2 = check_1; } os << "\n\n ." << std::endl; } 

Metode utama pengelompokan.

 std::ostream & operator<<(std::ostream & os, const K_means & k) { os << " : " << std::endl; for (int i = 0; i < k.k_pixcel; i++) { os << k.pixcel[i].r << " " << k.pixcel[i].g << " " << k.pixcel[i].b << " - №" << i << std::endl; } os << std::endl << "   : " << std::endl; for (int i = 0; i < k.q_klaster; i++) { os << k.centr[i].r << " " << k.centr[i].g << " " << k.centr[i].b << " - #" << i << std::endl; } os << "\n : " << k.q_klaster << std::endl; os << " : " << k.k_pixcel << std::endl; return os; } 

Output dari data awal.

Contoh keluaran

Contoh ini direncanakan sebelumnya, piksel dipilih secara khusus untuk demonstrasi. Dua iterasi sudah cukup bagi program untuk mengelompokkan data menjadi tiga kelompok. Melihat pusat dari dua iterasi terakhir, Anda dapat melihat bahwa mereka praktis tetap di tempatnya.

Yang lebih menarik adalah kasus piksel yang dihasilkan secara acak. Setelah menghasilkan 50 poin yang perlu dibagi menjadi 10 cluster, saya mendapat 5 iterasi. Setelah menghasilkan 50 poin yang perlu dibagi menjadi 3 kelompok, saya mendapatkan semua 100 iterasi maksimum yang diizinkan. Anda mungkin memperhatikan bahwa semakin banyak kluster, semakin mudah bagi program untuk menemukan piksel yang paling mirip dan menggabungkannya ke dalam kelompok yang lebih kecil, dan sebaliknya - jika ada beberapa kluster dan ada banyak titik, algoritme sering berakhir hanya ketika jumlah iterasi maksimum terlampaui, karena beberapa piksel terus melonjak. dari satu cluster ke yang lain. Namun, sebagian besar masih ditentukan dalam kelompok mereka sepenuhnya.

Nah, sekarang mari kita periksa hasil pengelompokan. Mengambil hasil dari beberapa cluster dari contoh 50 poin per 10 cluster, saya mengarahkan hasil data ini ke Illustrator dan inilah yang terjadi:



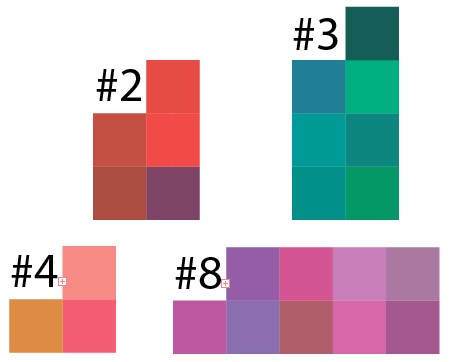
Dapat dilihat bahwa di setiap kluster ada nuansa warna yang berlaku, dan di sini Anda perlu memahami bahwa piksel dipilih secara acak, analog dari gambar seperti itu dalam kehidupan nyata adalah semacam gambar di mana semua warna secara tidak sengaja disemprotkan dan sulit untuk memilih area dengan warna yang sama.

Katakanlah kita punya foto seperti itu. Kita dapat mendefinisikan sebuah pulau sebagai satu kelompok, tetapi dengan peningkatan kita melihat bahwa pulau itu terdiri dari berbagai nuansa hijau.



Dan ini adalah cluster 8, tetapi dalam versi yang lebih kecil, hasilnya serupa:



Versi lengkap dari program ini dapat dilihat di GitHub saya.