Menghibur matematika. Sistem angka paling ekonomis

Kita semua tahu dari kursus sekolah apa sistem angka (SS) itu. Tetapi tidak semua orang berpikir tentang seberapa banyak SS itu. Yaitu set angka apa yang kita butuhkan untuk mewakili angka dalam SS ini. Ketika kita memiliki seperangkat elemen unik yang terbatas (kerikil multi-warna dengan ukuran berbeda) yang dapat digunakan untuk merepresentasikan angka, berapakah jumlah maksimum yang dapat kita wakili menggunakan elemen-elemen ini? (semua kerikil merah adalah nol, hijau adalah satu, biru adalah dua, dll., kecil adalah nol, sedang adalah yang pertama, besar adalah yang kedua, dll.). Di mana garis di mana pangkal SS memainkan peran yang lebih besar daripada kapasitas digit angka?

Ambil contoh n - jumlah elemen sama dengan 60. Setelah membagi elemen menjadi 2 kelompok (sistem angka biner) kita mendapatkan 30 digit. 30 unit adalah angka 30-bit terbesar dengan basis 2. Jika Anda menambahkan 1 ke dalamnya, Anda mendapatkan unit dengan 30 nol, mis. 2 di tanggal 30, karena masing-masing nol adalah kekuatan dua, dan angka dimulai dari 0, dan jangan lupa untuk mengurangi unit yang ditambahkan.

Untuk SS lainnya, sama $$$y = x ^ {60 / x} -1$di mana y adalah angka maksimum, x adalah basis derajat.

Poin Bangun:

$$$2 ^ {30} -1 = 1 \, 073 \, 741 \, 823$.
$$$3 ^ {20} -1 = 3 \, 486 \, 784 \, 400$.
$$$4 ^ {15} -1 = 1 \, 073 \, 741 \, 823$
$$$5 ^ {12} -1 = 244 \, 140 \, 624$
$$$6 ^ {10} -1 = 60 \, 466 \, $ 17$
$$$10 ^ {6} -1 = 999 \, $ 99$
$$$12 ^ {5} -1 = 248 \, $ 83$

Grafik fungsi:



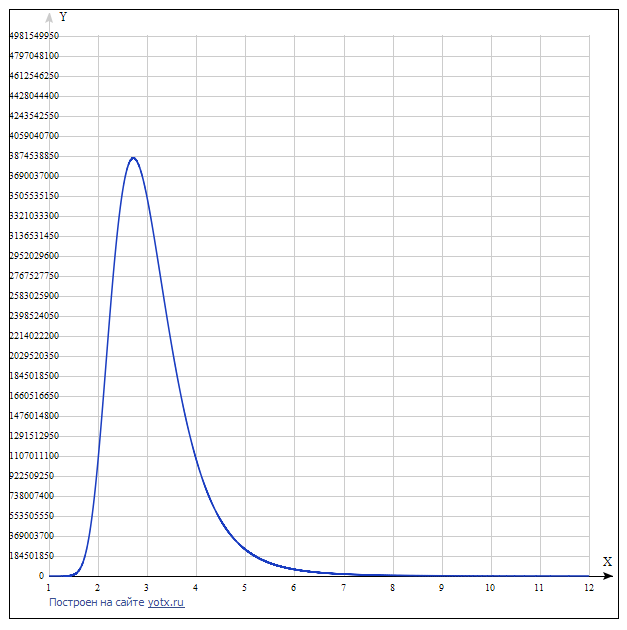
Grafik menunjukkan bahwa dengan peningkatan basis SS, dimulai dengan tiga, biaya meningkat dan fungsinya memiliki ekstrem atas. Membawanya ke bentuk umum, bisa Anda dapatkan $$$y = (\ sqrt [x] x) ^ {n} -1$, dan fungsi maksimum $$$\ sqrt [x] x$tercapai saat $$$x = e$.



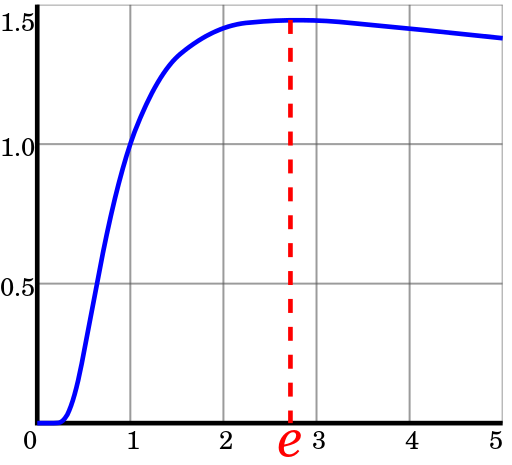
Grafik fungsi $$$y = \ sqrt [x] x$

Yaitu SS yang paling ekonomis adalah sistem sedekat mungkin $$$e$atau 3.

PS: Selain itu, SS dengan basis 3 adalah ganjil, yang berarti tidak memiliki masalah pembulatan (membawa 0,5 ke 0 atau ke 1), dan jika angka-angka ditulis secara simetris (-1.0.1 bukannya 0.1.2) maka kesederhanaan muncul mewakili angka negatif (10-1 adalah 8, -101 adalah -8, di mana minus bukanlah tanda, tetapi bagian dari digit yang dapat diganti dengan Z), tetapi ini adalah aritmatika yang sama sekali berbeda)))