Cara membuat lebih banyak status tidak valid bahkan lebih tak terkatakan

Belum lama berselang, sebuah artikel diterjemahkan di Habr tentang cara menggunakan tipe data aljabar untuk memastikan bahwa kondisi yang salah tidak dapat diekspresikan. Hari ini kita melihat cara yang sedikit lebih umum, scalable dan aman untuk mengekspresikan yang tak terungkapkan, dan Haskell akan membantu kita dalam hal ini.

Singkatnya, artikel itu membahas beberapa entitas dengan alamat surat dan alamat email, serta dengan syarat tambahan bahwa harus ada setidaknya salah satu dari alamat ini. Bagaimana cara diusulkan untuk mengekspresikan kondisi ini pada level tipe? Diusulkan untuk menulis alamat sebagai berikut:

type ContactInfo = | EmailOnly of EmailContactInfo | PostOnly of PostalContactInfo | EmailAndPost of EmailContactInfo * PostalContactInfo 

Masalah apa yang dimiliki pendekatan ini?

Yang paling jelas (dan dicatat beberapa kali dalam komentar pada artikel itu) adalah bahwa pendekatan ini sama sekali tidak dapat diskalakan. Bayangkan kita tidak memiliki dua jenis alamat, tetapi tiga atau lima, dan kondisi yang benar terlihat seperti "harus ada alamat surat, atau alamat email dan alamat kantor, dan seharusnya tidak ada beberapa alamat dengan jenis yang sama". Mereka yang ingin dapat menulis jenis yang sesuai sebagai latihan untuk menguji diri. Tugas dengan tanda bintang adalah untuk menulis ulang jenis ini dalam kasus ketika kondisi tentang tidak adanya duplikat telah hilang dari TOR.

Bagikan

Bagaimana cara mengatasi masalah ini? Mari kita coba berfantasi. Pertama-tama kami menguraikan dan memisahkan kelas alamat (misalnya, surat / email / nomor meja di kantor) dan konten yang sesuai dengan kelas ini:

 data AddrType = Post | Email | Office 

Kami belum akan memikirkan kontennya, karena tidak ada apa-apa tentang hal itu dalam kerangka referensi untuk validitas daftar alamat.

Jika kita memeriksa kondisi yang sesuai dalam runtime beberapa konstruktor dari beberapa bahasa OOP biasa, maka kita hanya akan menulis fungsi seperti

 valid :: [AddrType] -> Bool valid xs = let hasNoDups = nub xs == xs --      hasPost = Post `elem` xs hasEmail = Email `elem` xs hasOffice = Office `elem` xs in hasNoDups && (hasPost || (hasEmail && hasOffice)) 

dan akan membuang beberapa eksekusi jika mengembalikan False .

Bisakah kita memeriksa kondisi yang sama dengan bantuan pengatur waktu, saat kompilasi? Ternyata ya, kita bisa, jika jenis sistem bahasanya cukup ekspresif, dan sisa artikel kita akan memilih pendekatan ini.

Di sini tipe dependen akan banyak membantu kita, dan karena cara paling memadai untuk menulis kode yang divalidasi di Haskell adalah dengan menuliskannya di Agde atau Idris terlebih dahulu, kita akan mengganti sepatu kita dan menulis di Idris. Sintaks idris cukup dekat dengan Haskell: misalnya, dengan fungsi yang disebutkan di atas, Anda hanya perlu sedikit mengubah tanda tangan:

 valid : List AddrType -> Bool 

Sekarang ingat bahwa selain kelas-kelas alamat, kita juga membutuhkan isinya, dan menyandikan ketergantungan bidang pada kelas alamat sebagai GADT:

 data AddrFields : AddrType -> Type where PostFields : (city : String) -> (street : String) -> AddrFields Post EmailFields : (email : String) -> AddrFields Email OfficeFields : (floor : Int) -> (desk : Nat) -> AddrFields Office 

Yaitu, jika kita diberi nilai fields tipe AddrFields t , maka kita tahu bahwa t adalah beberapa AddrType AddrType dan fields berisi kumpulan bidang yang sesuai dengan kelas khusus ini.

 addrFields : AddrType -> Type addrFields Post = PostFields addrFields Email = EmailFields addrFields Office = OfficeFields 

Apa alamat lengkap dalam model ini? Ini adalah sepasang kelas alamat dan bidang terkait:

 Addr : Type Addr = (t : AddrType ** AddrFields t) 

Penggemar teori tipe akan mengatakan bahwa ini adalah tipe dependen eksistensial: jika kita diberi nilai tipe Addr , maka ini berarti bahwa ada nilai t tipe AddrType dan seperangkat bidang AddrFields t sesuai. Secara alami, alamat dari kelas yang berbeda memiliki tipe yang sama:

 someEmailAddr : Addr someEmailAddr = (Email ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (Office ** OfficeFields (-2) 762) 

Selain itu, jika EmailFields diberikan kepada kami, maka satu-satunya kelas alamat yang cocok adalah Email , sehingga Anda dapat menghilangkannya, timer akan mencetaknya sendiri:

 someEmailAddr : Addr someEmailAddr = (_ ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (_ ** OfficeFields (-2) 762) 

Kami menulis fungsi bantu yang memberikan daftar kelas alamat yang sesuai dari daftar alamat, dan segera menggeneralisasikannya untuk bekerja pada functor yang berubah-ubah:

 types : Functor f => f Addr -> f AddrType types = map fst 

Di sini, tipe Addr eksistensial berperilaku seperti pasangan yang akrab: khususnya, Anda dapat meminta komponen AddrType (tugas dengan tanda bintang: mengapa saya tidak bisa meminta komponen kedua?).

Angkat

Sekarang kita beralih ke bagian kunci dari cerita kita. Jadi, kami memiliki daftar alamat List Addr dan beberapa predikat yang valid : List AddrType -> Bool , yang pelaksanaannya untuk daftar ini kami ingin menjamin pada tingkat jenis. Bagaimana kita menggabungkannya? Tentu saja, tipe lain!

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst 

Sekarang kita akan menganalisis apa yang kita tulis di sini.

data ValidatedAddrList : List Addr -> Type where berarti bahwa jenis ValidatedAddrList parameter, pada kenyataannya, oleh daftar alamat.

Mari kita lihat tanda tangan dari satu-satunya konstruktor MkValidatedAddrList dari tipe ini: (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst . Artinya, dibutuhkan beberapa daftar alamat lst dan argumen lain dari tipe valid (types lst) = True . Apa arti tipe ini? Jadi itu berarti bahwa nilai di sebelah kiri = sama dengan nilai di sebelah kanan = , yaitu, valid (types lst) , pada kenyataannya, adalah Benar.

Bagaimana cara kerjanya? Tanda tangan = seperti (x : A) -> (y : B) -> Type . Yaitu, = mengambil dua nilai arbitrer x dan y (mungkin bahkan dari tipe A dan B , yang berarti bahwa ketidaksetaraan dalam idris heterogen, dan agak ambigu dari sudut pandang teori jenis, tetapi ini adalah topik untuk diskusi lain). Apa yang kemudian menunjukkan kesetaraan? Dan karena fakta bahwa satu-satunya konstruktor = - Refl dengan tanda tangan hampir (x : A) -> x = x . Artinya, jika kita memiliki nilai tipe x = y , maka kita tahu bahwa itu dibangun menggunakan Refl (karena tidak ada konstruktor lain), yang berarti x sebenarnya sama dengan y .

Perhatikan bahwa inilah mengapa dalam Haskell kita akan selalu berpura-pura bahwa kita sedang membuktikan sesuatu, karena Haskell telah undefined yang mendiami tipe apa pun, sehingga argumen di atas tidak bekerja di sana: untuk x , y istilah apa pun dari tipe x = y dapat dibuat melalui undefined (atau melalui rekursi tak terbatas, katakan bahwa pada umumnya sama dalam hal teori tipe).

Kami juga mencatat bahwa persamaan di sini tidak dimaksudkan dalam arti Haskell's Eq atau operator== dalam C ++, tetapi secara substansial lebih ketat: struktural, yang, menyederhanakan, berarti bahwa kedua nilai memiliki bentuk yang sama. Yaitu, untuk menipu dia sehingga tidak berfungsi. Tetapi masalah kesetaraan secara tradisional ditarik ke artikel terpisah.

Untuk mengkonsolidasikan pemahaman kita tentang kesetaraan, kami menulis unit test untuk fungsi yang valid :

 testPostValid : valid [Post] = True testPostValid = Refl testEmptyInvalid : valid [] = False testEmptyInvalid = Refl testDupsInvalid : valid [Post, Post] = False testDupsInvalid = Refl testPostEmailValid : valid [Post, Email] = True testPostEmailValid = Refl 

Tes-tes ini bagus karena Anda bahkan tidak perlu menjalankannya, sudah cukup bahwa taypcher memeriksanya. Memang, mari kita ganti True dengan False , misalnya, di bagian paling pertama dari mereka dan lihat apa yang terjadi:

 testPostValid : valid [Post] = False testPostValid = Refl 

Typsekher bersumpah

seperti yang diharapkan. Bagus

Sederhanakan

Sekarang mari kita refactor sedikit ValidatedAddrList kami.

Pertama, pola membandingkan nilai tertentu dengan True sangat umum, jadi ada tipe khusus So dalam idris untuk ini: Anda dapat mengambil So x sebagai sinonim untuk x = True . Mari kita perbaiki definisi ValidatedAddrList :

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : So (valid $ types lst)) -> ValidatedAddrList lst 

Selain itu, So memiliki fungsi bantu yang nyaman choose , yang pada dasarnya meningkatkan pemeriksaan ke tingkat jenis:

 > :doc choose Data.So.choose : (b : Bool) -> Either (So b) (So (not b)) Perform a case analysis on a Boolean, providing clients with a So proof 

Ini akan berguna bagi kita ketika kita menulis fungsi yang memodifikasi tipe ini.

Kedua, kadang-kadang (terutama dalam pengembangan interaktif) idris dapat menemukan nilai prf sesuai sendiri. Agar dalam kasus seperti itu tidak perlu membuatnya dengan tangan, ada gula sintaksis yang sesuai:

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> {auto prf : So (valid $ types lst)} -> ValidatedAddrList lst 

Kurung keriting berarti bahwa ini adalah argumen implisit bahwa idris akan mencoba menarik keluar dari konteks, dan auto berarti bahwa ia juga akan mencoba untuk membangunnya sendiri.

Jadi, apa yang diberikan ValidatedAddrList baru ini kepada kami? Dan itu memberikan rantai penalaran seperti itu: biarkan val menjadi nilai bertipe ValidatedAddrList lst . Ini berarti bahwa lst adalah daftar alamat, dan di samping itu, val dibuat menggunakan konstruktor MkValidatedAddrList , yang kami lewati ini dulu dan nilai prf lain dari tipe So (valid $ types lst) , yang hampir valid (types lst) = True . Dan agar kita dapat membangun prf , kita perlu, pada kenyataannya, untuk membuktikan bahwa kesetaraan ini berlaku.

Dan hal yang paling indah adalah bahwa ini semua diperiksa oleh tympher. Ya, pemeriksaan validitas harus dilakukan dalam runtime (karena alamat dapat dibaca dari file atau dari jaringan), tetapi timer akan memastikan bahwa pemeriksaan ini dilakukan: tanpa itu, tidak mungkin membuat ValidatedAddrList . Setidaknya di idris. Di Haskell, sayang.

Masukkan

Untuk memverifikasi verifikasi yang tidak terhindarkan, coba tulis fungsi untuk menambahkan alamat ke daftar. Upaya pertama:

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = MkValidatedAddrList (addr :: lst) 

Tidak, kesalahan ketik memberi pada jari (meskipun tidak terlalu mudah dibaca, biaya valid terlalu rumit):

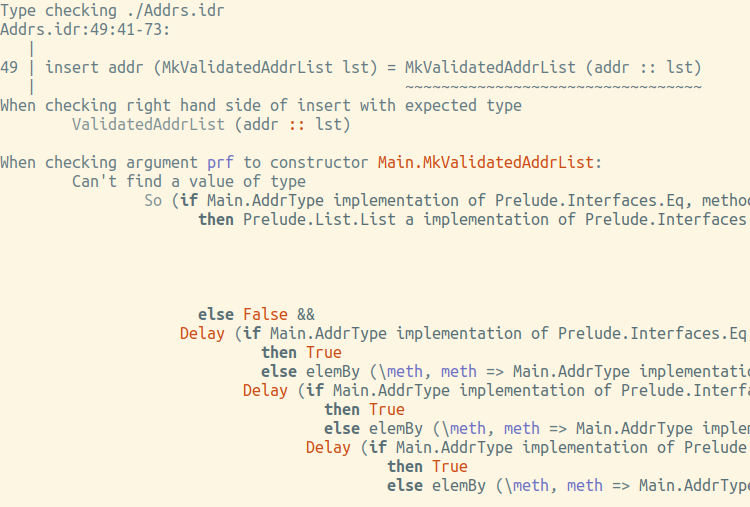
Bagaimana kita mendapatkan salinan dari So ini? Tidak ada yang lain selain choose disebutkan di atas. Upaya kedua:

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => MkValidatedAddrList (addr :: lst) Right r => ?rhs 

Hampir typechetsya. "Hampir" karena tidak jelas apa yang harus diganti dengan rhs . Sebaliknya, jelas: dalam hal ini, fungsi tersebut entah bagaimana harus melaporkan kesalahan. Jadi, Anda perlu mengubah tanda tangan dan membungkus nilai kembali, misalnya, di Maybe :

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Just $ MkValidatedAddrList (addr :: lst) Right r => Nothing 

Ini ubin dan berfungsi sebagaimana mestinya.

Tetapi sekarang muncul masalah yang tidak terlalu jelas berikut ini, yang sebenarnya, dalam artikel aslinya. Jenis fungsi ini tidak berhenti menulis implementasi seperti itu:

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = Nothing 

Artinya, kami selalu mengatakan bahwa kami tidak dapat membangun daftar alamat baru. Typhechaetsya? Ya Apakah benar Yah, hampir tidak. Bisakah ini dihindari?

Ternyata itu mungkin, dan kami memiliki semua alat yang diperlukan untuk ini. Jika berhasil, insert mengembalikan ValidatedAddrList , yang berisi bukti keberhasilan ini. Jadi tambahkan simetri elegan dan minta fungsi untuk mengembalikan juga bukti kegagalan!

 insert : (addr : Addr) -> ValidatedAddrList lst -> Either (So (not $ valid $ types (addr :: lst))) (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Right $ MkValidatedAddrList (addr :: lst) Right r => Left r 

Sekarang kita tidak bisa mengambil dan selalu mengembalikan Nothing .

Anda dapat melakukan hal yang sama untuk fungsi penghapusan alamat dan sejenisnya.

Mari kita lihat bagaimana hasilnya pada akhirnya.

Mari kita coba membuat daftar alamat kosong:

Tidak mungkin, daftar kosong tidak valid.

Bagaimana dengan daftar alamat surat saja?

Oke, mari kita coba memasukkan alamat surat ke dalam daftar yang sudah memiliki alamat surat:

Mari kita coba memasukkan email:

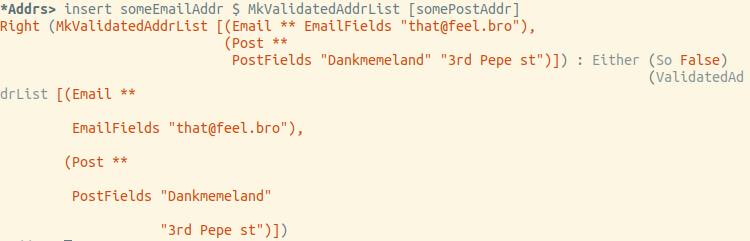
Pada akhirnya, semuanya bekerja persis seperti yang diharapkan.

Fiuh. Saya pikir itu akan menjadi tiga baris, tetapi ternyata sedikit lebih lama. Jadi untuk mengeksplorasi sejauh mana kita bisa pergi di Haskell, kita akan berada di artikel selanjutnya. Sementara itu, sedikit

Renungkan

Apa, pada akhirnya, keuntungan dari keputusan seperti itu dibandingkan dengan yang diberikan dalam artikel, yang kami rujuk di awal?

1. Sekali lagi, ini jauh lebih bisa diukur. Fungsi validasi kompleks lebih mudah ditulis.
2. Itu lebih terisolasi. Kode klien tidak harus tahu apa yang ada di dalam fungsi validasi, sedangkan formulir ContactInfo dari artikel asli mengharuskannya untuk diikat.
3. Logika validasi ditulis dalam bentuk fungsi biasa dan akrab, sehingga dapat segera diperiksa dengan bacaan yang bijaksana dan diuji dengan tes waktu kompilasi, daripada memperoleh makna validasi dari bentuk tipe data yang mewakili hasil yang sudah diverifikasi.
4. Menjadi mungkin untuk menentukan lebih akurat perilaku fungsi yang bekerja dengan tipe data yang menarik bagi kami, terutama dalam kasus kegagalan untuk lulus tes. Misalnya, insert ditulis sebagai hasilnya tidak mungkin ditulis secara salah . Demikian pula, orang dapat menulis insertOrReplace , insertOrIgnore dan sejenisnya, yang perilakunya sepenuhnya ditentukan dalam tipe.

Apa untungnya dibandingkan dengan solusi OOP seperti itu?

 class ValidatedAddrListClass { public: ValidatedAddrListClass(std::vector<Addr> addrs) { if (!valid(addrs)) throw ValidationError {}; } }; 

1. Kode lebih termodulasi dan aman. Dalam kasus di atas, cek adalah tindakan yang diperiksa sekali, dan tentang hal itu mereka kemudian lupa. Semuanya didasarkan pada kejujuran dan pemahaman bahwa jika Anda memiliki ValidatedAddrListClass , maka implementasinya pernah melakukan pemeriksaan di sana. Fakta cek ini dari kelas tidak dapat dipilih sebagai nilai tertentu. Dalam hal nilai dari beberapa tipe, nilai ini dapat ditransfer antara bagian-bagian berbeda dari program, digunakan untuk membangun nilai yang lebih kompleks (misalnya, sekali lagi, tolak pemeriksaan ini), selidiki (lihat paragraf berikutnya), dan umumnya melakukan hal yang sama seperti yang biasa kita lakukan dengan nilai-nilai.
2. Pemeriksaan semacam itu dapat digunakan dalam pencocokan pola (tergantung). Benar, tidak dalam kasus fungsi ini valid dan tidak dalam kasus idris, itu sangat rumit, dan idris sangat membosankan sehingga informasi yang berguna untuk pola dapat diekstraksi dari struktur yang valid . Meskipun demikian, valid dapat ditulis ulang dengan gaya pencocokan pola yang sedikit lebih ramah, tetapi ini berada di luar cakupan artikel ini dan umumnya tidak sepele.

Apa kerugiannya?

Saya hanya melihat satu kelemahan mendasar yang serius: valid adalah fungsi yang terlalu bodoh. Ini hanya mengembalikan sedikit informasi - apakah data telah lulus validasi atau tidak. Dalam hal tipe yang lebih pintar, kita bisa mencapai sesuatu yang lebih menarik.

Misalnya, bayangkan bahwa persyaratan untuk keunikan alamat telah hilang dari TK. Dalam kasus ini, jelas bahwa menambahkan alamat baru ke daftar alamat yang ada tidak akan membuat daftar tidak valid, sehingga kita dapat membuktikan teorema ini dengan menulis fungsi dengan tipe So (valid $ types lst) -> So (valid $ types $ addr :: lst) , dan menggunakannya, misalnya, untuk menulis tipe-aman selalu berhasil

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) 

Tetapi, sayangnya, teorema seperti rekursi dan induksi, dan masalah kita tidak memiliki struktur induktif yang elegan, oleh karena itu, menurut pendapat saya, kode dengan oak Boolean yang valid juga tidak buruk.