Pada artikel ini, kita akan membuat model pengendali berdasarkan pustaka standar pemodelan struktural (tanpa menggunakan pustaka blok regulasi fuzzy yang sudah jadi).
Sebagai objek kontrol, model mesin turbin gas dari buku teks V.I. Gosteva "Regulator fuzzy dalam sistem kontrol otomatis"
Mari kita membuat perbandingan dengan regulator PID dan SDA.
Pernyataan masalah
Perbedaan antara mesin turbin gas (mesin turbin gas) dan mesin turbojet (mesin turbojet) adalah bahwa dalam mesin turbin gas semua energi dihilangkan melalui poros. Dalam mesin turbojet, energi dilepaskan dalam bentuk aliran jet.
Mesin turbin gas (GTE) banyak digunakan dalam industri gas dan penerbangan, di mana mereka adalah dasar dari unit pompa gas dan pembangkit listrik pesawat, dalam penggerak generator turbo listrik industri pembangkit listrik puncak dan bergerak, di pembangkit listrik laut dan fasilitas industri lainnya di mana pengembangan kapasitas tunggal yang besar diperlukan (dari 1 hingga 25 MW) dalam satu unit dengan bobot dan dimensi minimum.
Serangkaian persyaratan diberlakukan pada mesin turbin gas yang terkait dengan keandalan, efisiensi energi, keselamatan, dan keramahan lingkungan selama operasi. Seiring dengan persyaratan ini, persyaratan untuk kualitas transien yang terkait dengan peluncuran unit, perubahan tajam dalam beban (daya) yang dipilih adalah relevan. Dalam banyak hal, kepuasan dari persyaratan ini terletak pada sistem kontrol otomatis (ACS) dari mesin turbin gas.
Mesin turbin gas khas yang digunakan dalam industri adalah mesin turboshaft, diagram yang ditunjukkan pada Gambar 1.
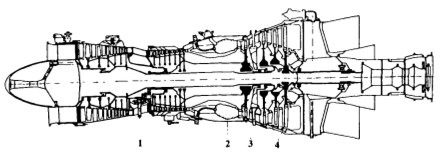
Gambar 1. Skema mesin turbin gas industri khas:
1- kompresor; 2 - ruang pembakaran; 3 - turbin kompresor; 4 - turbin listrik.
Mesinnya adalah mesin rotari di mana udara dikompres dalam kompresor 1, bahan bakar yang disuplai ke udara dibakar di ruang bakar 2, sebagian energi diambil dari gas panas di kompresor 3 turbin, dikonsumsi oleh kompresor 1 drive, 4 gas di turbin daya memperluas daya dibuat diambil dari mesin oleh konsumen.
Di sebagian besar mesin turbin gas, kecepatan rotor adalah kuantitas yang terkontrol. Sebagai faktor kontrol dalam ACS, kecepatan rotor n digunakan konsumsi bahan bakar GT di ruang bakar. Pada mode operasi yang berbeda dan dalam berbagai kondisi eksternal, parameter engine berubah secara signifikan.
Pertimbangkan mesin turbin gas (GTE) sebagai objek kontrol yang tidak stabil, di mana kecepatan rotor adalah variabel yang dikendalikan, dan konsumsi bahan bakar GT adalah tindakan kontrol. Meluruskan ketergantungan momen turbin - M T dan momen kompresor - M K , pada kecepatan rotor dan tidak memperhitungkan pengaruh kapasitas termal dan massa engine untuk mode operasi tertentu, catat fungsi transfer engine sebagai berikut:
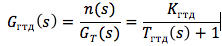
di mana gain dan konstanta waktu didefinisikan sebagai:
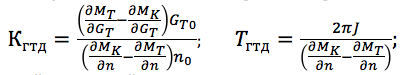
selain itu, sinyal input dan output dicatat dalam penyimpangan berdimensi relatif dari kondisi tunak (n = Δn / n 0 ; G T = ΔG / G TO , di mana nilai-nilai dasar dari parameter dipilih untuk mode operasi mesin tertentu, misalnya, diberi nilai atau maksimum). Pada mode operasi yang berbeda dan di bawah berbagai kondisi eksternal, gain dan konstanta waktu engine berubah secara signifikan, oleh karena itu, untuk setiap mode, perlu untuk menentukan nilai K GTD dan T GTD .
Perhatikan bahwa fungsi transfer G dari mesin turbin gas untuk objek kontrol yang tidak stabil, seperti mesin turbin gas, diperoleh dengan metode koefisien "beku" di bawah kondisi perubahan yang cukup lambat pada parameter objek.
Diagram blok dari sistem elektromekanis analog untuk secara otomatis mengendalikan kecepatan rotor suatu mesin ditunjukkan pada Gambar 2
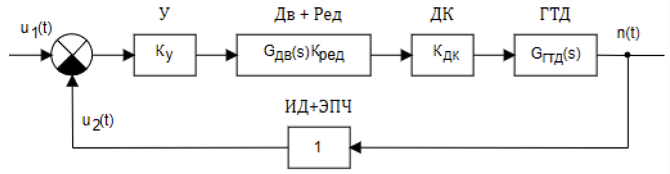
Gambar 2. Blok diagram GTE SAR analog
Frekuensi rotasi diatur oleh tegangan u 1 (t) dan diubah oleh sensor ID pulsa, frekuensi sinyal output yang ditentukan oleh ekspresi:
f = kmn, di mana n adalah jumlah putaran mesin, m adalah jumlah gigi gigi, k adalah rasio gigi. Tegangan bolak-balik yang diambil dari output ID menggunakan konverter frekuensi elektronik dari EPC dikonversi menjadi sinyal u2 (t), yang nilainya sebanding dengan jumlah putaran mesin - n. Tegangan u2 (t) dibandingkan dengan tegangan referensi dan sinyal kesalahan setelah amplifier U dipasok ke motor asinkron dua fase Dv, yang mengatur katup throttle dari DC melalui gearbox Merah, mengubah laju aliran bahan bakar memasuki mesin turbin gas. Sensor pulsa bersama dengan konverter frekuensi elektronik dapat dijelaskan oleh tautan proporsional dengan fungsi transfer yang sama dengan satu. Dalam hal ini, sistem itu sendiri memiliki umpan balik tunggal.
Mengingat koneksi serial dari penguat, motor induksi, katup throttle, unit turbin gas dan sensor frekuensi dengan konverter frekuensi elektronik sebagai objek kontrol umum, dan menggunakan regulator fuzzy digital, seluruh diagram blok dari Gambar 2 dapat direduksi menjadi diagram blok pada Gambar 3. Selain itu, semua fungsi transfer tautan direduksi menjadi fungsi transfer umum G0 (s).
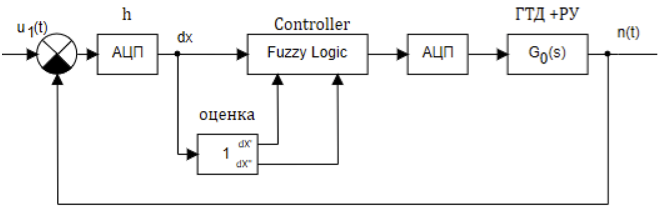
Gambar 3. Struktur sistem kontrol dengan pengontrol fuzzy.
Fungsi transfer umum G0 (s) dapat ditulis sebagai:
G 0 (s) = G (s) K EDIT TO G (s) = α [s (a + a) (s + b)] -1 , di mana
α = ab K K EDIT TO K ,
a = 1 / T DW ,
b = 1 / T GTE
Sebagai contoh, kami mengasumsikan bahwa ketergantungan fungsi transfer pada waktu operasi mengambil nilai-nilai berikut:
T GTD (t) = 0,9849 - 0,1188 × t + 0,0063 × t 2 - 0,00012 × t 3 ;
α (t) = 16,5475 - 4,4469 × t + 0,4843 × t 2 - 0,02315 × t 3 + 0,0004 × t 4 ;
T DW = 0,35 dtk.
Dalam studi sistem kontrol, kami mengasumsikan bahwa fungsi yang diberikan untuk mengubah kecepatan rotasi rotor mesin turbin gas diatur oleh tegangan input u (t)
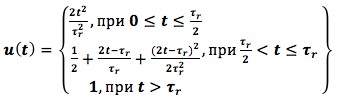
di mana τ adalah waktu akselerasi mesin. Kami mengambil τ r = 6 detik.
Membuat model yang dinamis
Model mesin yang disederhanakan disajikan pada Gambar 4. Dalam model ini, kami menggunakan parameter variabel blok tipikal yang berubah selama simulasi ketergantungan yang diberikan di atas.
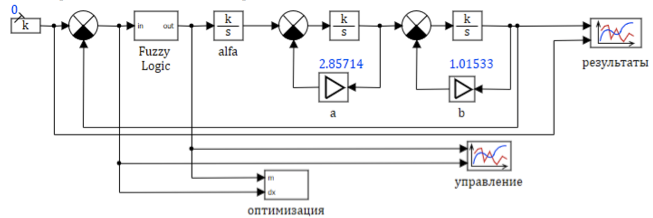
Gambar 4. Diagram struktural model mesin turbin gas
Koefisien amplifier alfa, a, b dihitung menggunakan bahasa scripting, teks program di bawah ini:
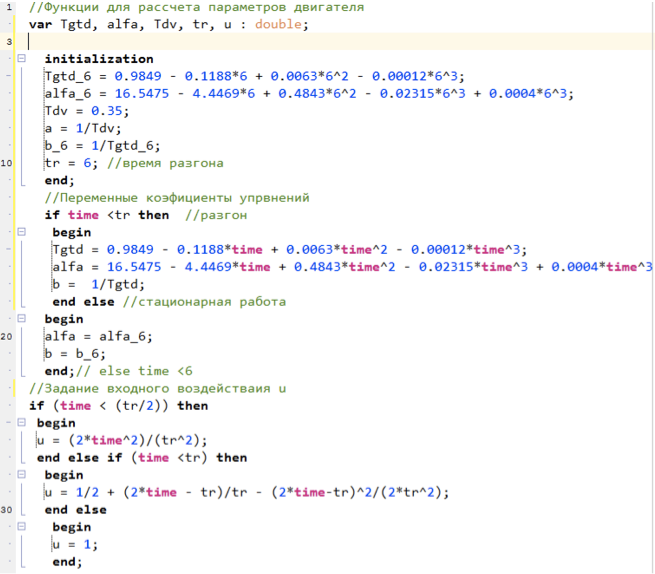
Gambar 5. Script untuk menghitung parameter model.
Tombol kontrol logika fuzzy
Regulator kontrol mengambil input ketidaksesuaian antara nilai yang ditetapkan dan nilai yang diperoleh dari model, dan harus menghitung tindakan kontrol.
Mari kita coba merakit pengontrol yang didasarkan pada logika fuzzy, hanya menggunakan blok standar pemodelan struktural matematis, tanpa menggunakan perpustakaan khusus.
Deskripsi prinsip kontrol berdasarkan logika fuzzy dapat ditemukan di artikel sebelumnya di hub, atau dalam deskripsi membuat perpustakaan khusus blok di sini (hati-hati, kata-kata kotor).
Kontroler apa pun yang didasarkan pada logika fuzzy melakukan urutan transformasi berikut:
- Pentahapan variabel input. Nilai variabel digantikan oleh seperangkat istilah.
- Aktivasi kesimpulan dari aturan logika fuzzy.
- Akumulasi kesimpulan untuk setiap variabel linguistik.
- Defazifikasi variabel keluaran.
Untuk mengendalikan mesin, kami akan menggunakan tiga variabel kontinu, yang dihitung berdasarkan satu sinyal:
- penyimpangan
- deviasi derivatif (tingkat perubahan deviasi);
- turunan kedua dari deviasi (percepatan perubahan penyimpangan).
Skema perhitungan disajikan pada Gambar 6:
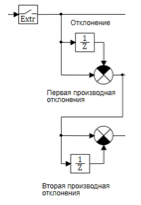
Gambar 6. Perhitungan penyimpangan derivatif pertama dan kedua.
Blok ekstrapolator mengukur sinyal yang memasuki pengontrol dengan periode 0,01 detik. Derivatif pertama dan kedua dihitung menggunakan rumus perbedaan:
dimana:
u (t) adalah penyimpangan saat ini pada waktu t;
u (t-Δt) adalah penyimpangan pada saat t - Δt;
u '(t) adalah nilai turunan dari penyimpangan pada saat t;
u '(t-Δt) adalah nilai turunan dari penyimpangan pada waktu t - Δt;
u '' (t) adalah nilai saat ini dari turunan kedua dari penyimpangan pada waktu t;
u '' (t-Δt) adalah nilai turunan kedua dari penyimpangan pada waktu t - Δt;
Ini adalah periode kuantisasi.
Pembagian dengan Δt dilakukan dalam unit perbandingan.
Sebagai hasil dari blok ini, tiga variabel linguistik dibuat: deviasi, variabel deviasi pertama, variabel deviasi kedua.
Untuk mengatasi masalah kontrol fuzzy, kami hanya akan menggunakan dua istilah untuk setiap variabel linguistik.
Penyimpangan - lebih sedikit, lebih banyak;
Derivatif pertama dari deviasi menurun, meningkat;
Derivatif kedua dari penyimpangan - melambat, berakselerasi.
Untuk menghitung nilai fungsi keanggotaan μ untuk setiap istilah, kami menggunakan fungsi linier dengan saturasi. Fungsi untuk istilah ini lebih dari 0 bila nilai input minimum dan 1 ketika nilai input maksimum. Untuk istilah yang lebih sedikit, fungsi ini mengambil nilai 1 saat variabel sama dengan minimum, dan 0 saat variabel maksimum. (lihat gambar 7)
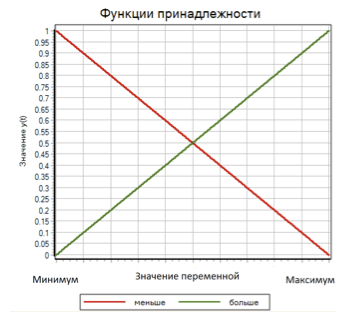
Gambar 7. Fungsi keanggotaan untuk istilah semakin sedikit.
Dengan demikian, untuk masing-masing dari tiga variabel input (deviasi, turunan pertama dari deviasi, turunan ke-2 dari deviasi), dua istilah semakin banyak muncul, nilai fungsi keanggotaan μ i yang bervariasi secara linear dari 0, ke 1 tergantung pada nilai input variabel.
Sebagai variabel linguistik keluaran, kami menggunakan efek keluaran, yang juga hanya memiliki dua istilah untuk dikurangi dan ditingkatkan.
Dari diagram model Gambar. 4 jelas bahwa jika penyimpangan kurang dari 0, maka nilainya lebih besar dari nilai yang ditentukan dan perlu dikurangi. Jika penyimpangan lebih besar dari 0, maka fungsinya kurang dari yang ditentukan dan perlu ditingkatkan.
Aturan logis untuk dua istilah akan terlihat seperti ini:
- Jika kurang dan menurun dan melambat => berkurang.
- Jika lebih dan meningkat dan mempercepat => meningkat.
Untuk mengaktifkan aturan inferensi fuzzy, kami menggunakan fungsi minimum untuk fuzzy dan operator. Nilai fungsi keanggotaan untuk ketentuan fungsi output dihitung dengan rumus:
μ
penurunan = MIN (μ
kurang , μ
berkurang , μ
melambat )
μ
meningkat = MIN (μ
lebih banyak , μ
meningkat , μ
berakselerasi )
Untuk memastikan konversi istilah menjadi nilai dampak spesifik (akumulasi dan denazifikasi), kami menggunakan algoritma Tsukamoto sebagai pusat gravitasi titik.
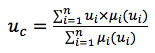dimana
u c adalah fungsi yang dihasilkan;
u i adalah nilai fungsi untuk istilah i;
μ i adalah nilai fungsi keanggotaan untuk syarat untuk fungsi tersebut.
Dalam kasus kami, fungsi yang dihasilkan untuk dua istilah dihitung dengan rumus:
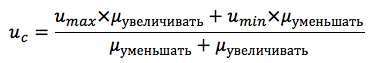
Skema umum dari algoritma inferensi fuzzy disajikan pada Gambar 8:
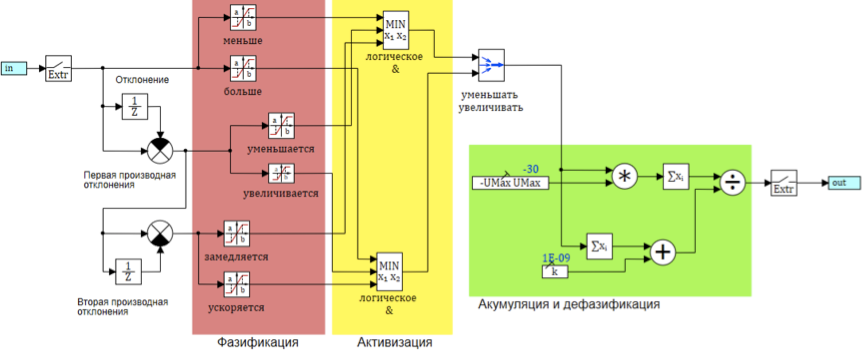
Gambar 8. Skema algoritma inferensi fuzzy
Agar algoritma ini berfungsi, kita harus menetapkan nilai minimum dan maksimum untuk 6 syarat dari tiga variabel linguistik (penyimpangan, turunan pertama dari penyimpangan, turunan ke-2 dari penyimpangan). Untuk mengurangi perhitungan, kita mengasumsikan bahwa penyimpangannya simetris terhadap nol. Maka cukup bagi kita untuk menemukan 3 nilai absolut, satu untuk setiap variabel.
deltMax - deviasi maksimum. Menetapkan nilai persyaratan lebih sedikit, lebih banyak (-deltMax, deltaMax);
divMax adalah turunan maksimum dari penyimpangan. Menetapkan nilai-nilai dari istilah menurun, meningkat (-divMax, divMax);
div2Max adalah turunan kedua maksimum. Menetapkan nilai dari istilah melambat, mempercepat (-div2Max, div2Max).
Efek maksimum dan minimum umin dan umax ditentukan oleh fitur desain dan dalam contoh ini diambil sama dengan +30 dan -30.
Penyesuaian regulator dengan optimasi.
Untuk memilih koefisien, kami menggunakan skema optimisasi yang sama yang kami gunakan dalam percobaan sebelumnya dengan logika fuzzy.
Sebagai kriteria optimisasi, kami mengambil simpangan baku tidak lebih dari 0,001 dan jumlah pergantian di unit kontrol tidak lebih dari 25. Untuk peralihan, kami mengambil perubahan dalam tanda aksi kontrol.
Rangkaian blok pengaturan pengontrol ditunjukkan pada Gambar. 9.
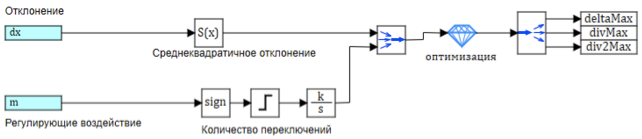
Gambar 9. Mengkonfigurasi parameter output fuzzy.
Sebagai hasil dari operasi blok, parameter berikut diperoleh
deltMax = 0,00746;
divMax = 0,2657;
div2Max = 25.13;
Hasil transisi disajikan pada Gambar 10.
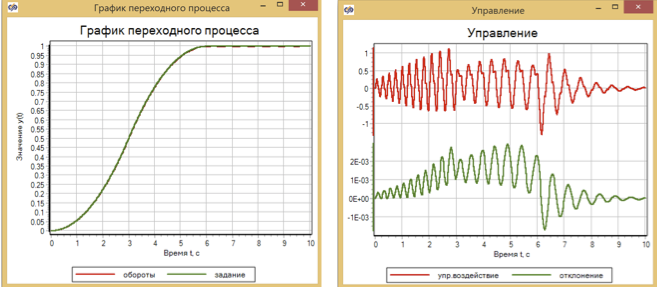
Gambar 10. Kontrol transien dan motorik menggunakan logika fuzzy.
Deviasi maksimum putaran dari set setelah optimasi adalah 2,5 × 10 -3 . Yang, pada prinsipnya, tidak buruk, tetapi dalam kitab V.I. Penyimpangan tamu dalam model setelah pengaturan adalah dua urutan besarnya lebih kecil: maksimumnya adalah 5 × 10 -5 .
Sebagai perbandingan, kami menyajikan hasil operasi pengontrol PID Gambar. 11 dan aturan lalu lintas Gambar. 12 untuk model yang sama dari mesin yang disederhanakan. Parameter regulator ini juga dipilih oleh metode optimasi.
Akibatnya, deviasi yang lebih besar diperoleh untuk pengontrol PID daripada pengontrol yang didasarkan pada logika fuzzy - sekitar 6 × 10 -3 , dan untuk pengontrol lalu lintas yang menggunakan turunan kedua, deviasinya sekitar 3 × 10 -3 (lihat 13). Terlebih lagi, pada semua grafik dapat dilihat bahwa ketika dampak yang ditentukan berubah (perubahan dalam bagian 3 detik, 6 detik), kualitas regulasi berubah.
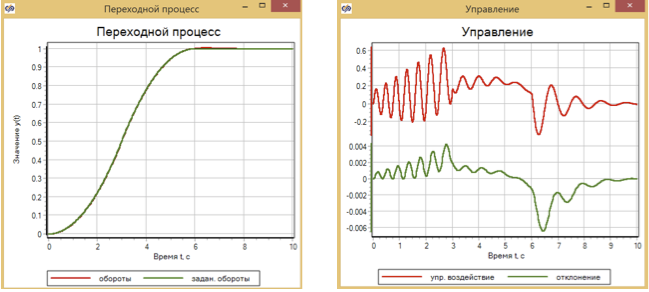
Gambar 11. Kontrol transien dan motorik menggunakan pengontrol PID.
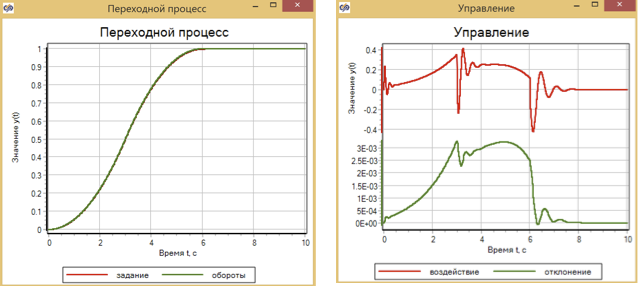
Gambar 12. Proses transien dan kontrol engine dengan bantuan pengontrol lalu lintas.
Untuk menghidupkan mesin, fungsi transisi digunakan dalam bentuk perubahan kecepatan yang mulus. Kami juga menyelaraskan regulator dengan metode optimisasi untuk kontrol optimal sesuai dengan hukum ini. Mari kita coba menerapkan efek bertahap dan melihat bagaimana regulator, awalnya dioptimalkan untuk proses transisi yang lancar, dapat mengatasinya.
Sebagai akibatnya, kami menggunakan langkah dari 0 hingga 1 pada 3 detik proses.
Hasil percobaan disajikan dalam gambar 13-15.
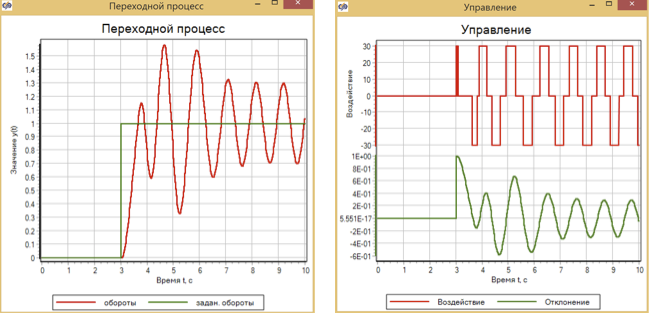
Gambar 13. Proses transien dan kontrol dengan aksi kontrol bertahap dengan pengontrol logika fuzzy.
Dapat dilihat bahwa sebuah regulator yang disetel untuk akselerasi mesin yang mulus tidak mengatasi kontrol selama tindakan bertahap, dan sistem memasuki mode osilasi otomatis.
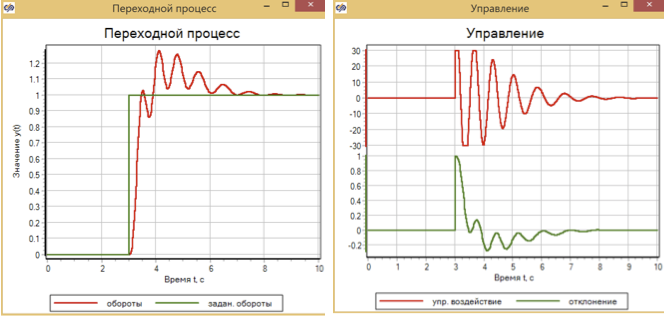
Gambar 14. Proses transien dan kontrol dengan aksi kontrol langkah dengan pengontrol PID.
Kontroler PID disetel ke proses yang mulus, dengan efek bertahap, memberikan transisi ke waktu yang telah ditentukan, tetapi pada saat yang sama ada overshoot 30% dan proses osilasi dalam waktu 4 detik.
Pengontrol lalu lintas, yang dikonfigurasikan untuk pengaturan yang mulus, memberikan transisi yang mulus tanpa overshoot selama pemaparan bertahap (Gbr. 14)
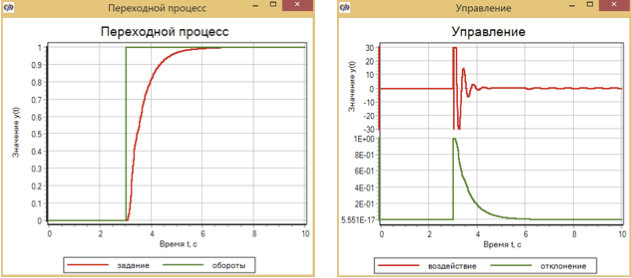
Gambar 15. Proses transisi dan kontrol dengan aksi kontrol bertingkat dengan pengontrol lalu lintas.
Kesimpulan
Eksperimen numerik ini menunjukkan bahwa pengontrol yang didasarkan pada logika fuzzy memberikan kontrol yang lebih akurat terhadap putaran model mesin sederhana dengan perubahan yang mulus pada nilai yang ditetapkan daripada PID dan SDA.
Namun, pengaturan seperti itu, ternyata, tidak menjamin stabilitas regulator selama tindakan bertahap.
Pada saat yang sama, untuk model mesin yang disederhanakan, pengontrol yang didasarkan pada logika fuzzy dalam hal tindakan bertahap ternyata lebih buruk daripada PID atau pengontrol lalu lintas.
Tautan ke arsip dengan proyek-proyek dari artikel untuk belajar sendiri