Implementasi algoritma Levenberg-Marquardt untuk mengoptimalkan jaringan saraf pada TensorFlow

Ini adalah tutorial perpustakaan TensorFlow. Anggap itu sedikit lebih dalam daripada di artikel tentang pengakuan angka tulisan tangan. Ini adalah tutorial tentang metode optimasi. Di sini Anda tidak dapat melakukannya tanpa matematika. Tidak apa-apa jika Anda benar-benar melupakannya. Ingat. Tidak akan ada bukti formal dan kesimpulan yang kompleks, hanya minimum yang diperlukan untuk pemahaman intuitif. Untuk mulai dengan, sedikit latar belakang tentang bagaimana algoritma ini dapat bermanfaat dalam mengoptimalkan jaringan saraf.

Enam bulan lalu, seorang teman meminta saya untuk menunjukkan cara membuat jaringan saraf dengan Python. Perusahaannya memproduksi instrumen untuk pengukuran geofisika. Beberapa probe berbeda selama pengeboran mengukur serangkaian sinyal yang terkait dengan parameter lingkungan di sekitar sumur. Dalam beberapa kasus kompleks, secara akurat menghitung parameter lingkungan dari sinyal untuk waktu yang lama bahkan pada komputer yang kuat, dan perlu untuk menafsirkan hasil pengukuran di lapangan. Ada ide untuk menghitung beberapa ratus ribu kasus pada sebuah cluster, dan untuk melatih jaringan saraf pada mereka. Karena jaringan saraf sangat cepat, dapat digunakan untuk menentukan parameter yang konsisten dengan sinyal yang diukur, tepat dalam proses pengeboran. Detail ada di artikel:

Kushnir, D., Velker, N., Bondarenko, A., Dyatlov, G., & Dashevsky, Y. (2018, 29 Oktober). Simulasi Real-Time Alat Tahanan Azimuthal Dalam dalam Model Kesalahan 2D Menggunakan Jaringan Saraf Tiruan (Rusia). Masyarakat Insinyur Perminyakan. doi: 10.2118 / 192573-RU

Suatu malam, saya menunjukkan bagaimana keras dapat menerapkan jaringan saraf sederhana, dan seorang teman di tempat kerja mulai berlatih tentang data yang dihitung. Setelah beberapa hari, kami mendiskusikan hasilnya. Dari sudut pandang saya, dia tampak menjanjikan, tetapi seorang teman mengatakan bahwa dia membutuhkan perhitungan dengan keakuratan perangkat. Dan jika rata - rata kesalahan kuadrat ternyata sekitar 1, maka 1e-3 diperlukan. 3 pesanan lebih sedikit. Seribu kali.

Eksperimen dengan arsitektur jaringan saraf, normalisasi data, dan pendekatan optimasi hampir tidak menghasilkan apa-apa. Beberapa minggu kemudian, seorang teman menelepon dan mengatakan bahwa dia menginstal MatLab dan menyelesaikan masalah dengan metode Levenberg-Marquardt (selanjutnya kita akan memanggil LM ). Itu dioptimalkan untuk waktu yang lama (beberapa hari), itu tidak berfungsi pada GPU, tetapi hasilnya adalah yang benar. Itu terdengar seperti sebuah tantangan.

Pencarian cepat untuk pengoptimal LM siap pakai untuk keras atau TensorFlow gagal. Saya hanya menemukan perpustakaan pyrenn, tetapi fungsinya bagi saya buruk. Saya memutuskan untuk mengimplementasikannya sendiri. Sekilas, semuanya tampak sederhana, dan dua malam sudah cukup. Butuh waktu lebih lama. Ada dua masalah:

1. TensorFlow. Banyak artikel, tetapi hampir semua level "tapi mari kita menulis halo pengakuan tulisan tangan dunia ."
2. Matematika Saya lupa banyak, dan penulis artikel matematika sama sekali tidak peduli dengan orang-orang seperti saya: rumus padat tanpa penjelasan, "jelas!" dan sebagainya.

Akibatnya, ia menulis artikel untuk mereka yang lupa matematika dan ingin memahami TensorFlow sedikit lebih dalam, tetapi tanpa hardcore. Artikel ini memiliki banyak teks dan kode kecil. Pilihan sebaliknya, ketika ada sedikit teks dan banyak kode, ada di sini Jupyter Notebook Levenberg-Marquardt .

Mengenal fitur Rosenbrock

Kami akan menghasilkan data pelatihan dengan fungsi Rosenbrock , yang sering digunakan sebagai tolok ukur untuk algoritma optimasi:

$$ $$f (x, y) = (a-x) ^ 2 + b (y-x ^ 2) ^ 2$$

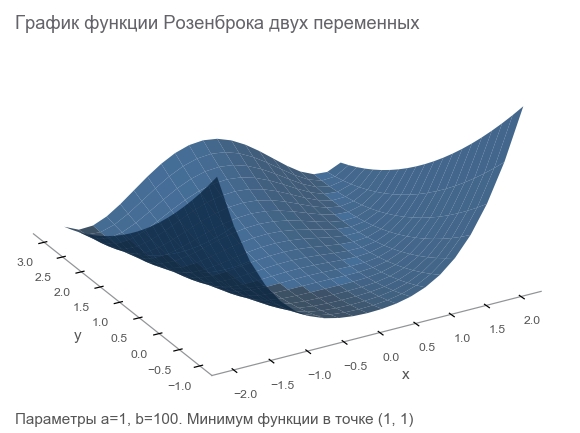
Kenapa dia baik?

• Jadwal yang indah. Ini disebut Lembah Rosenbrock dan fungsi pisang Rosenbrock yang tidak dapat diterjemahkan.
• Minimum global adalah di dalam lembah datar panjang, sempit, parabola. Menemukan lembah itu sepele, dan minimum global sulit.
• Ada opsi multidimensi. Tidak mudah menghasilkan fungsi yang baik untuk banyak variabel.

Kami akan mulai menulis kode dari itu dengan menghubungkan perpustakaan yang diperlukan untuk pekerjaan lebih lanjut:

import numpy as np import tensorflow as tf import math def rosenbrock(x, y, a, b): return (a - x)**2 + b*(y - x**2)**2 

Kami nyatakan masalahnya

Karena kita berbicara tentang alat pengukur, mari kita terus menggunakan analogi. Perangkat kami di dunia fiksi dapat mengukur koordinat $$$(x, y)$ dan tinggi $$$z$ . Fisikawan mempelajari dunia dan berkata: " Ya, ini Rosenbrock! Mengetahui koordinat, Anda dapat menghitung ketinggian secara akurat, Anda tidak perlu mengukurnya. " Dengan kata lain, para ilmuwan memberi kami sebuah model $$$z = rosenbrock (x, y, a, b)$ yang tergantung pada parameter $$$(a, b)$ . Parameter ini, meskipun konstan dalam dunia fiksi, tidak diketahui. Mereka perlu ditemukan.

Kami melakukan serangkaian percobaan yang memberi $$$m$ poin $$$(x_1, y_1, z_1), (x_2, y_2, z_2), ..., (x_m, y_m, z_m)$ :

 # (2.5, 2.5) -   ,  ,     data_points = np.array([[x, y, rosenbrock(x, y, 2.5, 2.5)] for x in np.arange(-2, 2.1, 2) for y in np.arange(-2, 2.1, 2)]) m = data_points.shape[0] 

Cara pertama untuk mengoptimalkan adalah mencoba dan menebak parameternya. Kami menggunakan perpustakaan Numpy:

 x, y = data_points[:, 0], data_points[:, 1] z = data_points[:, 2] #   =5  b=5? a_guess, b_guess = 5., 5. #  -hat   ,   , #   ,   ,   .   #     ^   - # .    hat. z_hat = rosenbrock(x, y, a_guess, b_guess) 

Bagaimana memahami betapa salahnya kita? Hitung residu - ukuran kesalahan. $$$m$ poin memberi $$$m$ residual - Anda memerlukan indikator integral. Kami mengurutkan setiap residual dalam kotak dan menghitung rata-rata:

$$ $$MSE (a, b) = \ frac {1} {m} \ sum_ {i = 1} ^ {m} (z_ {i} - \ widehat {z_ {i}}) ^ 2$$

Ukuran kedekatan ini disebut mean squared error (selanjutnya disebut sebagai mse ):

 # r - residuals () r = z - z_hat # mse loss = np.mean(r**2) print(loss) 

 [Out]: 3868.2291666666665 

Dengan meminimalkan mse , kami memecahkan masalah kuadrat terkecil ( minimalisasi kuadrat linier ):

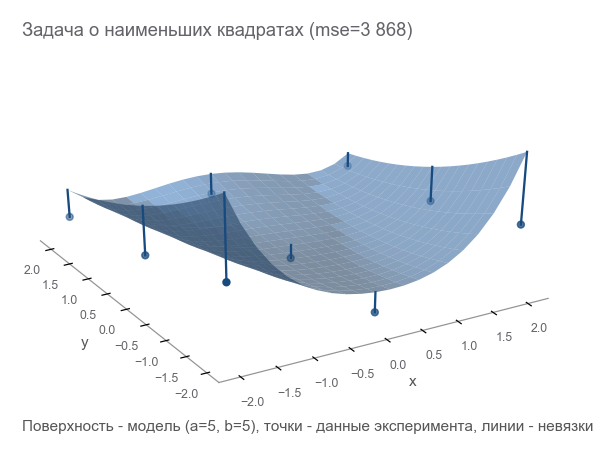
Dapat dilihat bahwa parameter tidak menebak sama sekali.

Kami merumuskan masalah pada TensorFlow

Model memiliki bentuk $$$z = rosenbrock (x, y, a, b)$ . Kami membawanya ke formulir $$$y = f (x, p)$ (biasanya matematika menulis $$$\ beta$ bukannya $$$p$ tetapi programmer tidak menggunakan beta). Sekarang model memiliki bentuk $$$y = rosenbrock (x, p)$ dimana $$$y$ - tinggi $$$x$ Apakah vektor koordinat dua elemen (komponen), dan $$$p$ - vektor parameter.

Pemrogram sering menganggap vektor sebagai array satu dimensi. Ini tidak sepenuhnya benar. Array angka adalah sarana untuk merepresentasikan vektor. Anda dapat mewakili vektor sebagai larik dimensi $$$N$ , array dua dimensi $$$1 \ kali N$ , dan bahkan sebuah array $$$N \ kali 1$ dalam kasus di mana fakta bahwa vektor adalah vektor kolom (misalnya, untuk mengalikan matriks dengan itu) adalah penting:

$$ $$\ begin {bmatrix} x_1 \\ vdots \\ x_N \ end {bmatrix}$$

TensorFlow menggunakan konsep tensor . Tensor , seperti array, dapat berupa satu dimensi (untuk merepresentasikan vektor ), dua dimensi (untuk matriks atau vektor kolom ) dan dimensi yang lebih besar.

 #    ('placeholder' ,    #      ) x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m]) #   ('variable' ,    ) #     (5, 5) p = tf.Variable([5., 5.], dtype=tf.float64) #  y_hat = rosenbrock(x[:, 0], x[:, 1], p[0], p[1]) #  r = y - y_hat # mse (mean squared error) loss = tf.reduce_mean(r**2) 

Kode TensorFlow tidak berbeda dalam bentuk dengan kode Numpy. Konten tersebut sangat besar. Kode numpy menghitung nilai mse. Kode TensorFlow sama sekali tidak melakukan perhitungan, ia membentuk grafik aliran data yang dapat dihitung oleh mse. Momen yang sangat toleran otak adalah pekerjaan dari fungsi rosenbrock . Kami menggunakannya dalam kedua kasus. Tetapi ketika kita melewati array Numpy, ia melakukan perhitungan sesuai dengan rumus dan mengembalikan angka. Dan ketika kita mentransfer tensor ke TensorFlow, ia membentuk subgraph dari aliran data dan mengembalikan edge -nya dalam bentuk tensor. Mukjizat polimorfisme, tetapi jangan menyalahgunakannya:

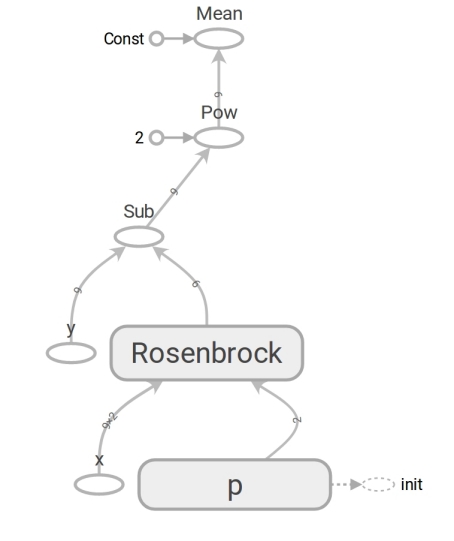
Berkat keberadaan grafik aliran data seperti itu, TensorFlow khususnya dapat menghitung turunan secara otomatis (menggunakan teknik diferensiasi otomatis mode balik ).

Momen matematika. Blok "untuk mereka yang lupa" akan disembunyikan di spoiler.

Kami membangun grafik aliran data, mari kita jalankan perhitungan mse:

 #        #      placeholder (  ) feed_dict = {x: data_points[:,0:2], y: data_points[:,2]} #       TensorFlow session = tf.Session() #     session.run(tf.global_variables_initializer()) #   ()  loss (mse) current_loss = session.run(loss, feed_dict) print(current_loss) 

 [Out]: 3868.2291666666665 

Hasilnya sama dengan Numpy. Jadi mereka tidak salah.

Mulai optimalkan

Sayangnya, tidak mungkin untuk menebak parameternya. Tapi kemudian kita:

1. Kami menetapkan kriteria optimalitas - nilai minimum mse.
2. Parameter variabel ditentukan: vektor $$$p$ dengan komponen $$$a$ , $$$b$ Fungsi Rosenbrock.
3. Kami belum memikirkan keterbatasan, tetapi belum ada.

Pada langkah terakhir, kami membuat grafik aliran data dengan tensor loss hingga ( fungsi hilang ). Tujuan optimasi adalah untuk menemukan nilai vektor parameter $$$p$ di mana nilai fungsi kerugian minimal. Kami beruntung, grafik fungsi ini sangat sederhana (cekung dan tanpa minimum lokal):

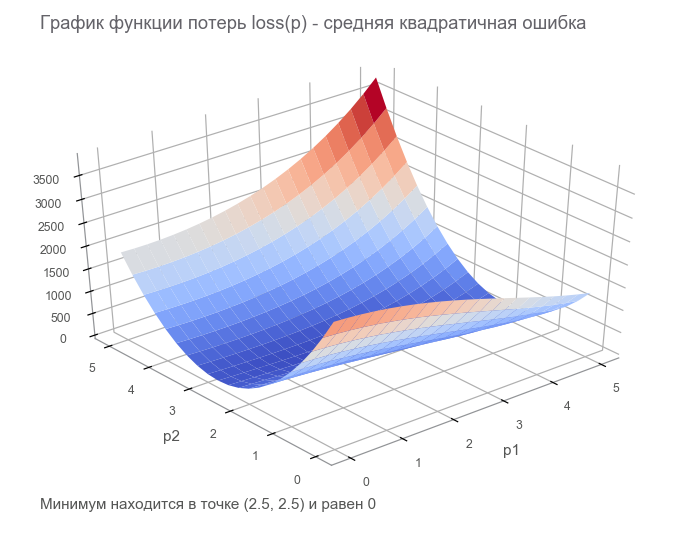
Memulai dengan optimasi. Untuk memulai, kami menulis siklus umum:

 # :   mse,   ,  #   mse,        placeholder def train(target_loss, max_steps, loss_tensor, train_step_op, inputs): step = 0 current_loss = session.run(loss_tensor, inputs) #           while current_loss > target_loss and step < max_steps: step += 1 #    1, 2, 4, 8, 16...  if math.log(step, 2).is_integer(): print(f'step: {step}, current loss: {current_loss}') #    session.run(train_step_op, inputs) current_loss = session.run(loss_tensor, inputs) print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}') 

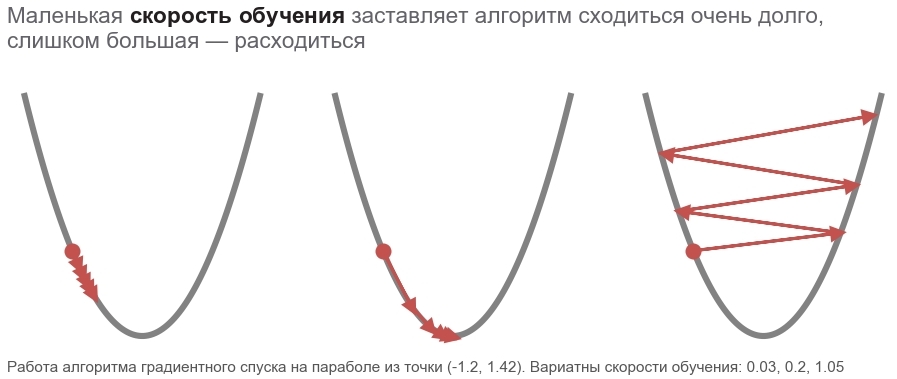
Kami mengoptimalkan dengan metode penurunan gradien tercepat (SGD)

Tindakan metode ini dapat dibandingkan dengan mengendarai pemain ski yang berani, yang selalu menempatkan lereng (ke arah yang paling curam). Dalam hal ini, hanya kemiringan pada titik lokasi yang diperhitungkan. Dan jika kemiringannya kuat, maka pemain ski itu terbang jauh sebelum perubahan berikutnya. Dengan kemiringan yang lemah, ia bergerak dalam langkah-langkah kecil. Mungkin cara terbang menjadi pohon ( Algoritma menyimpang ), dan terjebak dalam lubang ( minimum lokal ).

Anda dapat menulis sebagai berikut (ubah $$$\ boldsymbol {p}$ pada $$$\ boldsymbol {p} - ...$ ):

$$ $$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - \ alpha [\ nabla_ {p} loss (\ boldsymbol {p})]$$

Berminyak $$$\ boldsymbol {p}$ menekankan bahwa ini adalah titik lokasi aktual - nilai vektor parameter pada langkah saat ini. Pada langkah pertama, ini adalah dugaan kami (5, 5). Ada dua poin menarik dalam rumus: $$$\ alpha$ - Tingkat pembelajaran ( learning rate ), $$$\ nabla_ {p} loss$ - gradien ( gradien ) dari fungsi yang hilang oleh vektor parameter.

 #        grad = tf.gradients(loss, p)[0] #   learning_rate = 0.0005 #   ,     apply_gradients - #         opt = tf.train.GradientDescentOptimizer(learning_rate=1) #           sgd = opt.apply_gradients([(learning_rate*grad, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, sgd, feed_dict) print('PARAMETERS:', session.run(p)) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 1381.5379689135807 [...] ENDED ON STEP: 582, FINAL LOSS: 9.698531012270816e-11 PARAMETERS: [2.50000205 2.49999959] 

Butuh 582 langkah:

Kami mengoptimalkan dengan metode Adam

Kami tidak akan melangkah lebih jauh ke metode gradien, tetapi ada banyak variasi. Anda dapat membacanya di artikel Metode Pengoptimalan Jaringan Saraf Tiruan . Di TensorFlow, banyak pengoptimal sudah diterapkan. Sebagai contoh, Adam:

 #       , #      adm = tf.train.AdamOptimizer(15).minimize(loss) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, adm, feed_dict) print('PARAMETERS:', session.run(p)) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 34205.72916492336 [...] ENDED ON STEP: 317, FINAL LOSS: 2.424142714263483e-12 PARAMETERS: [2.49999969 2.50000008] 

Dikelola dalam 317 langkah. Jauh lebih cepat.

Kami mengoptimalkan dengan metode Newton

Tindakan metode orde kedua dapat dibandingkan dengan mengendarai snowboarder freeride rasional yang merenungkan titik berikutnya dari rutenya untuk waktu yang lama dan memperhitungkan tidak hanya kemiringan di lokasi, tetapi juga kelengkungan.

Faktanya, kedua metode gradient descent dan second-order mencoba menebak ( memperkirakan ) fungsi pada titik saat ini. Metode gradien hanya fokus pada kemiringan grafik fungsi pada titik - turunan pertama. Metode orde kedua, selain bias, memperhitungkan kelengkungan akun, turunan kedua: "jika kelengkungan berlanjut, lalu di mana minimumnya?" Kami menghitung dan pergi ke sana:

Untuk membangun perkiraan seperti itu dan menghitung estimasi titik minimum, Anda dapat menggunakan seri Taylor . Untuk kasus satu dimensi, aproksimasi oleh polinomial orde kedua pada titik tersebut $$$a$ terlihat seperti ini:

$$ $$f (x) \ kira-kira f (a) + \ frac {f '(a) (x-a)} {1!} + \ frac {f' '(a) (x-a) ^ 2} {2!}$$

Minimum tercapai pada $$$x = a - \ frac {f '(a)} {f' '(a)}$ . Kasus multidimensi terlihat lebih serius:

Perkiraan polinomial orde kedua untuk fungsi vektor melalui gradien dan matriks Hessian pada suatu titik $$$a$ terlihat seperti ini:

$$ $$f (x) \ kira-kira f (a) + (xa) ^ \ intercal [\ nabla_ {x} f (a)] + \ frac {1} {2!} (xa) ^ \ intercal [\ boldsymbol {H } f_ {x} (a)] (xa)$$

Minimum tercapai pada $$$x = a - [\ boldsymbol {H} f_ {x} (a)] ^ {- 1} [\ nabla_ {x} f (a)]$ . Bentuknya hampir bertepatan dengan kasus satu dimensi: kami mengganti turunan pertama dengan gradien, yang kedua dengan matriks Hessian dan membuat koreksi untuk bekerja dengan vektor. Tidak mungkin untuk membagi vektor dengan matriks, oleh karena itu, perkalian dengan matriks invers digunakan. T berarti transpos . Rumus menyiratkan bahwa secara default vektor adalah kolom. Transpose mengubah vektor kolom menjadi vektor baris . Ketika menerapkan pada TensorFlow, ini harus diperhitungkan, tetapi dalam arah yang berlawanan: secara default, vektor adalah string (tensor satu dimensi). Untuk jaga-jaga: transposisi bukan rotasi 90 derajat, itu adalah transformasi baris menjadi kolom dalam urutan yang sama.

Jadi, langkah metode Newton memiliki bentuk berikut:

$$ $$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - [\ boldsymbol {H} loss_ {p} (\ boldsymbol {p})] ^ {- 1} [\ nabla_ {p} loss (\ boldsymbol {p} )]$$

TensorFlow memiliki segalanya untuk mengimplementasikan metode ini:

 #        hess = tf.hessians(loss, p)[0] #    - grad_col = tf.expand_dims(grad, -1) # ,      dp = tf.matmul(tf.linalg.inv(hess), grad_col) #  -  - dp = tf.squeeze(dp) #  p  dp    newton = opt.apply_gradients([(dp, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, newton, feed_dict) print('PARAMETERS:', session.run(p)) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 105.04357496954218 step: 4, current loss: 9.96663526704236 ENDED ON STEP: 6, FINAL LOSS: 5.882202372519996e-20 PARAMETERS: [2.5 2.5] 

Cukup 6 langkah:

Dioptimalkan oleh algoritma Gauss-Newton

Metode Newton memiliki satu kelemahan - matriks Hessian. Berkat TensorFlow kita dapat menghitungnya dalam satu baris kode. Menurut wiki, Johann Karl Friedrich Gauss membuat penyebutan pertama tentang metodenya pada 1809. Perhitungan matriks Hessian untuk beberapa parameter untuk metode kuadrat terkecil dapat memakan banyak waktu. Sekarang kita dapat mengasumsikan bahwa algoritma Gauss-Newton menggunakan perkiraan matriks Hessian melalui matriks Jacobi untuk menyederhanakan perhitungan. Tetapi dari sudut pandang sejarah, ini tidak benar: Ludwig Otto Hesse (yang mengembangkan matriks yang dinamai menurut namanya) lahir pada tahun 1811 - 2 tahun setelah penyebutan algoritma yang pertama. Dan Carl Gustav Jacobi berusia 5 tahun.

Algoritma Gauss-Newton tidak bekerja dengan fungsi kerugian. Ini bekerja dengan fungsi residual $$$r (p)$ . Fungsi ini mengambil vektor input parameter $$$p$ dan mengembalikan vektor residual . Dalam kasus kami, vektor $$$p$ terdiri dari 2 komponen (parameter $$$a$ dan $$$b$ Fungsi Rosenbrock), dan vektor sisa dari $$$m$ komponen (sesuai dengan jumlah percobaan). Fungsi vektor dari argumen vektor diperoleh. Turunannya:

Agar tidak bingung dalam kelimpahan karakter, kami menganggap itu $$$\ boldsymbol {J} _ {r}$ - Matriks Jacobi dari fungsi residual pada titik saat ini $$$\ boldsymbol {p}$ . Kemudian algoritma Gauss-Newton dapat ditulis sebagai berikut:

$$ $$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - [\ boldsymbol {J} _ {r} ^ \ intercal \ boldsymbol {J} _ {r}] ^ {- 1} \ boldsymbol {J} _ {r } ^ \ intercal r (\ boldsymbol {p})$$

Merekam dalam bentuk benar-benar bertepatan dengan rekaman metode Newton. Hanya alih-alih matriks Hessian digunakan $$$\ boldsymbol {J} _ {r} ^ \ intercal \ boldsymbol {J} _ {r}$ bukannya gradien $$$\ boldsymbol {J} _ {r} ^ \ intercal r (\ boldsymbol {p})$ . Selanjutnya, kita akan melihat mengapa pendekatan seperti itu dapat digunakan. Sementara itu, mari kita lanjutkan ke implementasi di TensorFlow:

 #  ,  TensorFlow     , #   ,        #  .  ,   : # 1)       tf.unstack(r) # 2)      tf.gradients(r_i, p) # 3)       tf.stack #      ,     #       j = tf.stack([tf.gradients(r_i, p)[0] for r_i in tf.unstack(r)]) jT = tf.transpose(j) #     - r_col = tf.expand_dims(r, -1) #      hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r_col) # ,      dp = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) #  -  - dp = tf.squeeze(dp) #  p  dp    ng = opt.apply_gradients([(dp, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, ng, feed_dict) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 14.653025157673625 step: 4, current loss: 4.3918079172783016e-07 ENDED ON STEP: 4, FINAL LOSS: 3.374364957618591e-17 PARAMETERS: [2.5 2.5] 

Cukup 4 langkah. Kurang dari untuk metode Newton.

Seperti dapat dilihat dari kode, fungsi kerugian tidak digunakan dalam optimisasi, hanya untuk kriteria berhenti dan masuk. Bagaimana algoritma pengoptimalan mengetahui fungsi mana yang harus diminimalkan? Jawabannya mengejutkan: tidak mungkin! Gauss-Newton hanya meminimalkan kesalahan kuadrat rata-rata .

Perbaiki bagian matematika dari artikel

Kami mengulangi semua matematika yang kami butuhkan. Mari kita perbaiki sedikit agar lebih fokus hanya pada pemrograman dan TensorFlow. Anda mungkin perlu pensil untuk melacak urutan tindakan matematika.

Ada modelnya $$$y = f (x, p)$ dimana $$$x$ - vektor $$$p$ - vektor parameter dimensi $$$n$ , dan $$$y$ - skalar. Dari percobaan yang diterima $$$m$ poin $$$(x_ {1}, y_ {1}), ..., (x_ {m}, y_ {m})$ ( pasangan data ). Fungsi residual vektor hanya bergantung pada vektor parameter: $$$r (p) = (r_ {1} (p), ... r_ {m} (p))$ dimana $$$r_ {k} (p) = y_ {k} - \ widehat {y_ {k}} = y_ {k} - f (x_ {k}, p)$ . , $$$p$ , $$$x_{k}, y_{k}$ ? , $$$x_{k}, y_{k}$ , .

$$$p$ , ( sum of squared error — sse residual sum-of-squares — rss ) . mse sse , $$$m$ . . :

$$ $$loss(p) = r_{1}^2(p) + \cdots + r_{m}^2(p) = \sum_{k=1}^{m} r_{k}^2(p)$$

$$$p$ $$$(p)$ .

, . — . — , $$$r^2$ $$$2r \frac{\partial r}{\partial p}$ . :

$$ $$\nabla_{p}loss = (\sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{1}}, \cdots, \sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{n}})$$

. :

$$ $$[\boldsymbol{H}loss_{p}]_{ij} = \frac{\partial^2 loss}{\partial p_{i} \partial p_{j}} = \sum_{k=1}^{m}(2\frac{\partial r_{k}}{\partial p_{i}}\frac{\partial r_{k}}{\partial p_{j}} + 2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}})$$

. , , $$${(uv)}'={u}'v+u{v}'$ .
Hebat! .

, , , — $$$2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$ . , , $$$r_{k}$ , . — . , ? -.

:

$$ $$\boldsymbol{J}_{r} = \begin{pmatrix} \frac{\partial r_{1}}{\partial p_{1}} & \cdots & \frac{\partial r_{1}}{\partial p_{n}}\\ \vdots & \ddots & \vdots \\ \frac{\partial r_{m}}{\partial p_{1}} & \cdots & \frac{\partial p_{m}}{\partial p_{n}} \end{pmatrix}$$

, , . Perhatikan bahwa:

$$ $$2\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r} \approx \boldsymbol{H}loss_{p}$$

"" . ( ). , — $$$2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$, .
( ):

$$ $$2\boldsymbol{J}_{r}^\intercal r = \nabla_{p}loss$$

, , - — , mse .

. , , . $$$m$$$$(x_{1}, y_{1}), ..., (x_{m}, y_{m})$, $$$y = rosenbrock(x, p)$. $$$p$, .

, : " . - ! ". , , , ( supervised learning ). , . : ( training set ) — ; — ( prediction model ) ; — , .

( multi-layer perceptron neural network mlp ). , , :

• ( starting values ) . Xavier'a, .
• ( overfitting ). — . , . — .
• ( scaling of the input ). , .

9 . 500:

 #    def get_random_rosenbrock_data_points(m): result = np.zeros((m, 3)) result[:, 0] = np.random.uniform(-2, 2, m) result[:, 1] = np.random.uniform(-2, 2, m) result[:, 2] = rosenbrock(result[:, 0], result[:, 1], 2.5, 2.5) return result m = 500 data_points = get_random_rosenbrock_data_points(m) # overfitting   ,      validation_data_points = get_random_rosenbrock_data_points(m) 

500 . — ( learner ), ( outcome measurement ) ( features ) .

( network diagram ). MatLab:

( input ). $$$W$( weights ) 2x10, $$$b$( bias ) 10, ( activation ). () ( hidden layer ) 10 . , , ( output ).

, , ( $$$tanh$):

$$ $$\begin{matrix} h_{1} = tanh(xW_{1} + b_{1})\\ \widehat{y} = h_{1}W_{2} + b_{2} \end{matrix}$$

:

$$ $$h_1 = tanh(\begin{bmatrix} x_1 & x_2 \end{bmatrix}\begin{bmatrix} w^{(1)}_{1,1} & \cdots& w^{(1)}_{1,10} \\ w^{(1)}_{2,1} &\cdots& w^{(1)}_{2,10} \end{bmatrix} + \begin{bmatrix} b^{(1)}_1 & \cdots & b^{(1)}_{10} \end{bmatrix}) \\ \widehat{y} = \begin{bmatrix}h^{(1)}_1 & \cdots & h^{(1)}_{10}\end{bmatrix} \begin{bmatrix} w^{(2)}_{1,1} \\ \vdots \\ w^{(2)}_{1,10} \\ \end{bmatrix} + b_2$$

. $$$W_{1}$"" $$$h_{1}$, - $$$W_{2}$. 41 . , .

$$$m \times 2$, . - $$$\widehat{y}$dari $$$m$:

 #     10 "" n_hidden = 10 #      Xavier'a initializer = tf.contrib.layers.xavier_initializer() #    x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m, 1]) #         W1 = tf.Variable(initializer([2, n_hidden], dtype=tf.float64)) b1 = tf.Variable(initializer([1, n_hidden], dtype=tf.float64)) #   ,  tanh   h1 = tf.nn.tanh(tf.matmul(x, W1) + b1) #        W2 = tf.Variable(initializer([n_hidden, 1], dtype=tf.float64)) b2 = tf.Variable(initializer([1], dtype=tf.float64)) #   y_hat = tf.matmul(h1, W2) + b2 #  r = y - y_hat #   mse     loss = tf.reduce_mean(tf.square(r)) #      placeholder feed_dict = {x: data_points[:,0:2], y: data_points[:,2:3]} validation_feed_dict = {x: validation_data_points[:,0:2], y: validation_data_points[:,2:3]} 

Adam

Adam $$$rosenbrock$. mse :

 #    adm = tf.train.AdamOptimizer(1e-2).minimize(loss) session.run(tf.global_variables_initializer()) #   ,    40000  train(1e-10, 40000, loss, adm, feed_dict) print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict))) 

 [Out]: step: 1, current loss: 671.4242576535694 [...] ENDED ON STEP: 40000, FINAL LOSS: 0.22862158574440725 VALIDATION LOSS: 0.29000289644978866 

. : , , .

$$$rosenbrock$2 . :

• . 9 , 500. .
• . - $$$p$, .

:

 #      y   x def jacobian(y, x): loop_vars = [ tf.constant(0, tf.int32), tf.TensorArray(tf.float64, size=m), ] #  -   #      _, jacobian = tf.while_loop( lambda i, _: i < m, #           #   (-),   x     lambda i, res: (i+1, res.write(i, tf.reshape(tf.gradients(y[i], x), (-1,)))), loop_vars) #       return jacobian.stack() #       r_flat = tf.squeeze(r) #        #       parms = [W1, b1, W2, b2] parms_sizes = [tf.size(p) for p in parms] j = tf.concat([jacobian(r_flat, p) for p in parms], 1) jT = tf.transpose(j) #           hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r) 

$$$\boldsymbol{J}r_{p}$. , 4 $$$W_1, b_1, W_2, b_2$. 4 $$$\boldsymbol{J}r_{W_1}, \boldsymbol{J}r_{b_1}, \boldsymbol{J}r_{W_2}, \boldsymbol{J}r_{b_2}$tf.concat .

. tf.while_loop , $$$r_i$, , stack .

$$$r_i$$$$W_1$: $$$\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} \\ \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$. tf.reshape (-1,) $$$\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} & \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$.

. - . — TensorFlow . — - - $$$W_1, b_1, W_2, b_2$. -. Levenberg-Marquardt Jupyter Notebook rosenbrock_train.py . , TensorFlow . - , ( ) , , .

-

hess_approx grad_approx -. $$$rosenbrock$, . :

1. : $$$\Delta \boldsymbol{p} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} & \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} & \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} & \Delta b_2\end{bmatrix}$
2. :
   $$$\Delta W_{1} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$, $$$\Delta b_{1} = \begin{bmatrix} \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} \end{bmatrix}$, $$$\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} \end{bmatrix}$, $$$\Delta b_{2} = \begin{bmatrix} \Delta b_2\end{bmatrix}$.
3. , :
   $$$\Delta W_{1} = \begin{bmatrix} \Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{1,10} \\ \Delta w^{(1)}_{2,1} &\cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$, $$$\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} \\ \vdots \\ \Delta w^{(2)}_{1,10} \\ \end{bmatrix}$
4. .

 # 1.     dp_flat = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) # 2.     dps = tf.split(dp_flat, parms_sizes, 0) # 3.     for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4.  :       gn = opt.apply_gradients(zip(dps, parms)) #   session.run(tf.global_variables_initializer()) train(1e-10, 100, loss, gn, feed_dict) 

 [Out]: step: 1, current loss: 548.8468777701685 step: 2, current loss: 49648941.340197295 InvalidArgumentError: Input is not invertible. 

- . , . - , .

, .

-

. Matlab trainlm . . MathWorks.

- : $$$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$. - :

$$ $$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}+\mu \boldsymbol{I}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$$

$$$\ mu$$$$I$$$$n$( ). $$$\ mu$, -. , . , LM -.

:

 mu = tf.placeholder(tf.float64, shape=[1]) n = tf.add_n(parms_sizes) I = tf.eye(n, dtype=tf.float64) # 1.     dp_flat = tf.matmul(tf.linalg.inv(hess_approx + tf.multiply(mu, I)), grad_approx) # 2.     dps = tf.split(dp_flat, parms_sizes, 0) # 3.     for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4.  :       lm = opt.apply_gradients(zip(dps, parms)) 

$$$\ mu$? LM - . , . , $$$\ mu$, . — , mse . , :

 #       store = [tf.Variable(tf.zeros(p.shape, dtype=tf.float64)) for p in parms] #  TensorFlow       save_parms = [tf.assign(s, p) for s, p in zip(store, parms)] restore_parms = [tf.assign(p, s) for s, p in zip(store, parms)] #   mu    3. feed_dict[mu] = np.array([3.]) step = 0 session.run(tf.global_variables_initializer()) #    mse current_loss = session.run(loss, feed_dict) #    100   while current_loss > 1e-10 and step < 100: step += 1 #  1, 2, 4...   if math.log(step, 2).is_integer(): print(f'step: {step}, mu: {feed_dict[mu][0]} current loss: {current_loss}') #    session.run(save_parms) # ,     mse while True: #    session.run(lm, feed_dict) new_loss = session.run(loss, feed_dict) if new_loss > current_loss: #  -  mu  10     feed_dict[mu] *= 10 session.run(restore_parms) else: #  -  mu  10     feed_dict[mu] /= 10 current_loss = new_loss break print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}') print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict))) 

 [Out]: step: 1, mu: 3.0 current loss: 692.6211687622557 [...] ENDED ON STEP: 100, FINAL LOSS: 0.012346989371823602 VALIDATION LOSS: 0.01859463694102034 

100 LM mse 10 , 40 .

. , . , rosenbrock_train.py .

2D . . . , " " ( curse of dimentionality , Bellman, 1961). . .

:

$$ $$f(\boldsymbol{x}) = \sum_{i=1}^{N-1}\left [ 100(x_{i+1} - x_{i}^2)^2 + (1-x_{i})^2 \right ], \boldsymbol{x}=[x_1 \cdots x_{N}]\in \mathbb{R}^N$$

rosenbrock_train.py get_rand_rosenbrock_points .

-

- : " ! 4 , 300! ". , ( ) -. , , . - . . : ? , . . , - :

1. 10 000 6D .
2. 3 12, 10, 8 (311 ).
3. .
4. 3.5 .

. - 2 . LM . 20 .

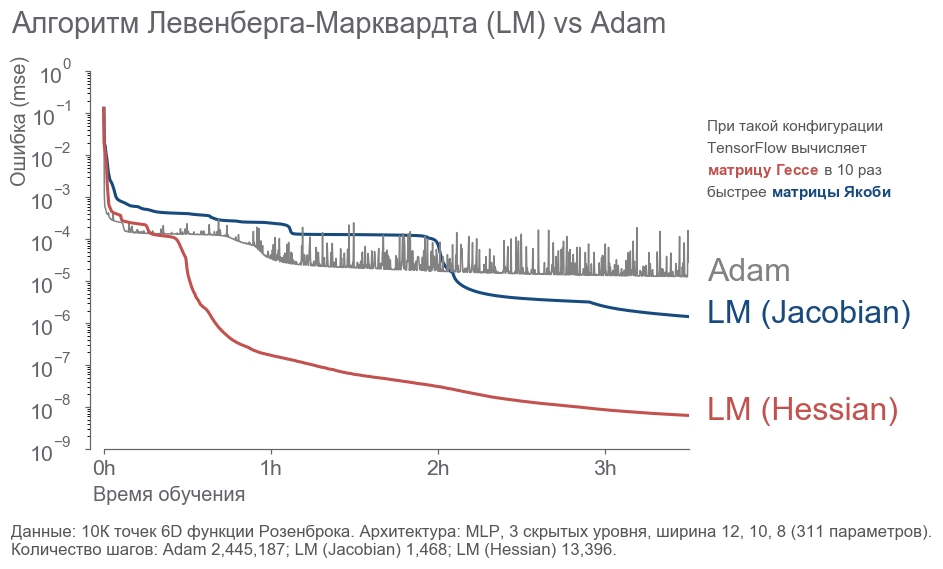
rosenbrock_train.py . . , .

Kesimpulan

, . " ", , . , . , 273 . - , .

, :

1. .
2. ( ) -:
   [1] Petros Drineas, Ravi Kannan, and Michael W. Mahoney. 2006. Fast Monte Carlo Algorithms for Matrices I: Approximating Matrix Multiplication. SIAM J. Comput. 36, 1 (July 2006), 132-157. DOI= http://dx.doi.org/10.1137/S0097539704442684
   [2] Adelman, M., & Silberstein, M. (2018). Faster Neural Network Training with Approximate Tensor Operations. CoRR, abs/1805.08079.

, - . , . "".