Geekly articles weekly

Kami memperkirakan fungsi menggunakan jaringan saraf

Untuk mengembangkan perpustakaan untuk bekerja dengan jaringan saraf, kami akan memecahkan masalah mendekati fungsi argumen tunggal menggunakan algoritma jaringan saraf untuk pelatihan dan prediksi.


Entri


Biarkan fungsi f diberikan: [x0, x1] -> R


Kami memperkirakan fungsi yang diberikan f oleh rumus


P(x) = SUM W[i]*E(x,M[i])

dimana


  • i = 1..n
  • M [i] dari R
  • W [i] dari R
  • E (x, M) = {0, untuk x <M; 1/2, dengan x = M; 1, untuk x> M

Jelas, dengan distribusi yang seragam dari nilai-nilai M [i] pada interval (x0, x1), ada jumlah seperti W [i] di mana rumus P (x) akan paling mendekati fungsi f (x). Selain itu, untuk nilai M [i] yang diberikan didefinisikan pada interval (x0, x1) dan dipesan dalam urutan naik, kita dapat menggambarkan algoritma berurutan untuk menghitung jumlah W [i] untuk rumus P (x).


Dan di sini adalah jaringan saraf


Kami mengubah rumus P (x) = SUM W [i] * E (x, M [i]) menjadi model jaringan saraf dengan satu input neuron, satu output neuron, dan n neuron layer tersembunyi


 P(x) = SUM W[i]*S(K[i]*x + B[i]) + C

dimana


  • variabel x - "input" layer yang terdiri dari satu neuron
  • {K, B} - parameter dari lapisan "tersembunyi", terdiri dari n neuron dan fungsi aktivasi - sigmoid
  • {W, C} - parameter dari layer "output", yang terdiri dari satu neuron, yang menghitung jumlah bobot inputnya.
  • S adalah sigmoid,

sementara


  • parameter awal dari layer "hidden" K [i] = 1
  • parameter awal dari layer "tersembunyi" B [i] didistribusikan secara merata pada segmen (-x1, -x0)

Semua parameter jaringan saraf K, B, W, dan C ditentukan dengan melatih jaringan saraf pada sampel (x, y) dari nilai-nilai fungsi f.


Sigmoid


Sigmoid adalah fungsi nonlinear meningkatkan monotonik halus


  • S (x) = 1 / (1 + exp (-x)).

Programnya


Kami menggunakan paket Tensorflow untuk menggambarkan jaringan saraf kami.


 #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost)

Pelatihan


 init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values })

Teks lengkap


 import math import numpy as np import tensorflow as tf import matplotlib.pyplot as plt x0, x1 = 10, 20 #    test_data_size = 2000 #      iterations = 20000 #    learn_rate = 0.01 #   hiddenSize = 10 #    #     def generate_test_values(): train_x = [] train_y = [] for _ in range(test_data_size): x = x0+(x1-x0)*np.random.rand() y = math.sin(x) #   train_x.append([x]) train_y.append([y]) return np.array(train_x), np.array(train_y) #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) if(_ % 1000 == 999): print("cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values }))) train_dataset, train_values = generate_test_values() train_values1 = session.run(model, feed_dict={ x: train_dataset, }) plt.plot(train_dataset, train_values, "bo", train_dataset, train_values1, "ro") plt.show() with tf.variable_scope("hidden", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("hidden:") print("kernel=", w.eval()) print("bias = ", b.eval()) with tf.variable_scope("output", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("output:") print("kernel=", w.eval()) print("bias = ", b.eval())

Itulah yang terjadi



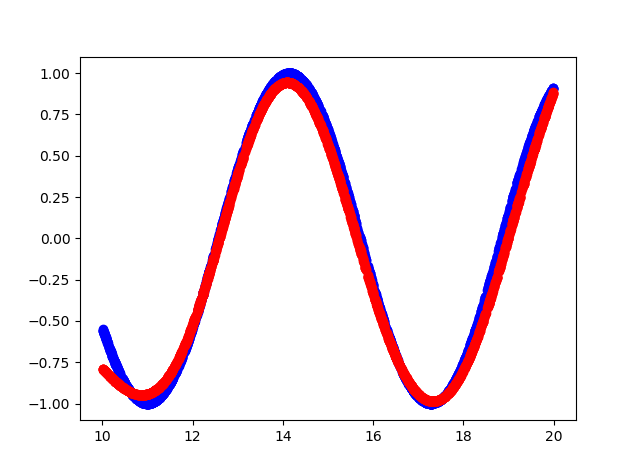
  • Biru adalah fungsi aslinya.
  • Warna merah - perkiraan fungsi

Output konsol


 cost = 0.15786637365818024 cost = 0.10963975638151169 cost = 0.08536215126514435 cost = 0.06145831197500229 cost = 0.04406769573688507 cost = 0.03488277271389961 cost = 0.026663536205887794 cost = 0.021445846185088158 cost = 0.016708852723240852 cost = 0.012960446067154408 cost = 0.010525770485401154 cost = 0.008495906367897987 cost = 0.0067353141494095325 cost = 0.0057082874700427055 cost = 0.004624188877642155 cost = 0.004093789495527744 cost = 0.0038146725855767727 cost = 0.018593043088912964 cost = 0.010414039716124535 cost = 0.004842184949666262 hidden: kernel= [[1.1523403 1.181032 1.1671464 0.9644377 0.8377886 1.0919508 0.87283015 1.0875995 0.9677301 0.6194152 ]] bias = [-14.812331 -12.219926 -12.067375 -14.872566 -10.633507 -14.014006 -13.379829 -20.508204 -14.923473 -19.354435] output: kernel= [[ 2.0069902 ] [-1.0321712 ] [-0.8878887 ] [-2.0531905 ] [ 1.4293027 ] [ 2.1250408 ] [-1.578137 ] [ 4.141281 ] [-2.1264815 ] [-0.60681605]] bias = [-0.2812019]

Kode sumber


https://github.com/dprotopopov/nnfunc

Source: https://habr.com/ru/post/id428281/

More articles:


All Articles