Saya sajikan kepada Anda terjemahan sebuah bab dari buku Hands-On Data Science dengan Anaconda
“Analitik data prediktif - pemodelan dan validasi”
Tujuan utama kami dalam melakukan berbagai analisis data adalah mencari pola untuk memprediksi apa yang akan terjadi di masa depan. Untuk pasar saham, peneliti dan pakar melakukan berbagai tes untuk memahami mekanisme pasar. Dalam hal ini, Anda dapat mengajukan banyak pertanyaan. Apa yang akan menjadi tingkat indeks pasar dalam lima tahun ke depan? Berapa kisaran harga berikutnya untuk IBM? Akankah volatilitas pasar meningkat atau menurun di masa depan? Apa dampaknya jika pemerintah mengubah kebijakan pajaknya? Apa keuntungan dan kerugian potensial jika satu negara memulai perang dagang dengan negara lain? Bagaimana kita memprediksi perilaku konsumen dengan menganalisis beberapa variabel terkait? Bisakah kita memprediksi kemungkinan bahwa seorang mahasiswa pascasarjana akan berhasil lulus? Bisakah kita menemukan hubungan antara perilaku spesifik dari satu penyakit tertentu?
Karena itu, kami akan mempertimbangkan topik-topik berikut:
- Memahami Analisis Data Prediktif
- Kumpulan data yang berguna
- Peramalan Acara Masa Depan
- Pemilihan model
- Uji Kausalitas Granger
Memahami Analisis Data Prediktif
Orang mungkin memiliki banyak pertanyaan tentang acara mendatang.
- Seorang investor, jika dia bisa memprediksi pergerakan harga saham di masa depan, dia bisa mendapat untung besar.
- Perusahaan, jika mereka dapat memprediksi tren produk mereka, mereka dapat meningkatkan harga saham dan pangsa pasar mereka.
- Pemerintah, jika mereka dapat memprediksi dampak populasi yang menua pada masyarakat dan ekonomi, mereka akan memiliki lebih banyak insentif untuk mengembangkan kebijakan yang lebih baik dalam hal anggaran negara dan keputusan strategis terkait lainnya.
- Universitas, jika mereka dapat dengan baik memahami permintaan pasar dalam hal kualitas dan keterampilan untuk lulusan mereka, mereka dapat mengembangkan serangkaian program yang lebih baik atau meluncurkan program baru untuk memenuhi kebutuhan tenaga kerja di masa depan.
Untuk prognosis yang lebih baik, peneliti harus mempertimbangkan banyak pertanyaan. Misalnya, apakah data sampel terlalu kecil? Bagaimana cara menghapus variabel yang hilang? Apakah kumpulan data ini bias dalam hal prosedur pengumpulan data? Bagaimana perasaan kita tentang ekstrem atau emisi? Apa itu musim dan bagaimana kita menghadapinya? Model apa yang harus kita gunakan? Bab ini akan membahas beberapa masalah ini. Mari kita mulai dengan dataset yang berguna.
Kumpulan data yang berguna
Salah satu sumber data terbaik adalah
UCI Machine Learning Repository . Setelah mengunjungi situs kami akan melihat daftar berikut:

Misalnya, jika Anda memilih dataset pertama (Abalon), kita akan melihat yang berikut ini. Untuk menghemat ruang, hanya bagian atas yang ditampilkan:

Dari sini, pengguna dapat mengunduh dataset dan menemukan definisi variabel. Kode berikut dapat digunakan untuk memuat dataset:
dataSet<-"UCIdatasets" path<-"http://canisius.edu/~yany/RData/" con<-paste(path,dataSet,".RData",sep='') load(url(con)) dim(.UCIdatasets) head(.UCIdatasets)
Output yang sesuai ditunjukkan di sini:

Dari kesimpulan sebelumnya, kita tahu bahwa di set data ada 427 pengamatan (set data). Untuk masing-masing dari mereka, kami memiliki 7 fungsi terkait, seperti
Nama, Data_Tip, Default_Task, Attribute_Types, N_In Situ (jumlah instance),
N_Attributes (jumlah atribut) dan
Tahun . Variabel yang disebut
Default_Task dapat diartikan sebagai penggunaan utama dari setiap kumpulan data. Misalnya, dataset pertama yang disebut
Abalone dapat digunakan untuk
Klasifikasi . Fungsi
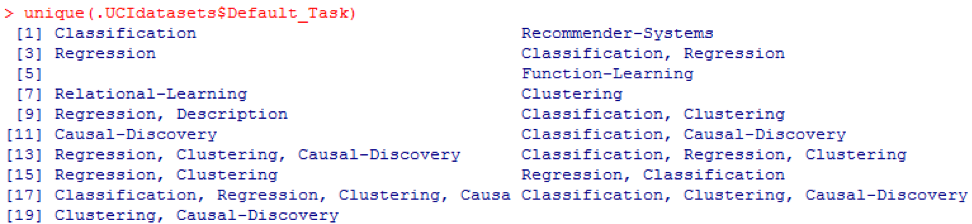
unik () dapat digunakan untuk mencari semua
Default_Task yang mungkin ditampilkan di sini:
Paket R AppliedPredictiveModeling
Paket ini mencakup banyak kumpulan data berguna yang dapat digunakan untuk bab ini dan lainnya. Cara termudah untuk menemukan kumpulan data ini adalah dengan fungsi
help () yang ditampilkan di sini:
library(AppliedPredictiveModeling) help(package=AppliedPredictiveModeling)
Di sini kami menunjukkan beberapa contoh memuat dataset ini. Untuk memuat satu set data, kami menggunakan fungsi
data () . Untuk dataset pertama yang disebut
abalone , kami memiliki kode berikut:
library(AppliedPredictiveModeling) data(abalone) dim(abalone) head(abalone)
Outputnya adalah sebagai berikut:

Terkadang, satu set data besar mencakup beberapa set sub-data:
library(AppliedPredictiveModeling) data(solubility) ls(pattern="sol")
[1] "solTestX" "solTestXtrans" "solTestY" [4] "solTrainX" "solTrainXtrans" "solTrainY"
Untuk memuat setiap kumpulan data, kita bisa menggunakan fungsi
dim () ,
head () ,
tail () dan
ringkasan () .
Analisis Rangkaian Waktu
Rangkaian waktu dapat didefinisikan sebagai satu set nilai yang diperoleh pada saat-saat bersamaan, seringkali dengan interval yang sama di antara mereka. Ada periode yang berbeda, seperti tahunan, triwulanan, bulanan, mingguan, dan harian. Untuk deret waktu PDB (produk domestik bruto) biasanya kita gunakan triwulanan atau tahunan. Untuk kutipan - frekuensi tahunan, bulanan dan harian. Dengan menggunakan kode berikut, kami dapat memperoleh data PDB AS triwulanan dan untuk periode tahunan:
ath<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPannual)
YEAR GDP 1 1930 92.2 2 1931 77.4 3 1932 59.5 4 1933 57.2 5 1934 66.8 6 1935 74.3
dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPquarterly)
DATE GDP_CURRENT GDP2009DOLLAR 1 1947Q1 243.1 1934.5 2 1947Q2 246.3 1932.3 3 1947Q3 250.1 1930.3 4 1947Q4 260.3 1960.7 5 1948Q1 266.2 1989.5 6 1948Q2 272.9 2021.9
Namun, kami memiliki banyak pertanyaan untuk analisis deret waktu. Misalnya, dari sudut pandang ekonomi makro, kita memiliki siklus bisnis atau ekonomi. Industri atau perusahaan mungkin memiliki musim. Misalnya, menggunakan industri pertanian, petani akan menghabiskan lebih banyak di musim semi dan musim gugur dan lebih sedikit di musim dingin. Untuk pengecer, mereka akan memiliki arus uang yang besar pada akhir tahun.
Untuk memanipulasi seri waktu, kita bisa menggunakan banyak fitur berguna yang termasuk dalam paket R, yang disebut
timeSeries . Dalam contoh, kami mengambil data rata-rata harian dengan frekuensi mingguan:
library(timeSeries) data(MSFT) x <- MSFT by <- timeSequence(from = start(x), to = end(x), by = "week") y<-aggregate(x,by,mean)
Kita juga bisa menggunakan fungsi
head () untuk melihat beberapa pengamatan:
head(x)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-09-28 60.8125 61.8750 60.6250 61.3125 26180200 2000-09-29 61.0000 61.3125 58.6250 60.3125 37026800 2000-10-02 60.5000 60.8125 58.2500 59.1250 29281200 2000-10-03 59.5625 59.8125 56.5000 56.5625 42687000 2000-10-04 56.3750 56.5625 54.5000 55.4375 68226700
head(y)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-10-04 59.6500 60.0750 57.7000 58.5500 40680380 2000-10-11 54.9750 56.4500 54.1625 55.0875 36448900 2000-10-18 53.0375 54.2500 50.8375 52.1375 50631280 2000-10-25 61.7875 64.1875 60.0875 62.3875 86457340 2000-11-01 66.1375 68.7875 65.8500 67.9375 53496000
Peramalan Acara Masa Depan
Ada banyak metode yang bisa kita gunakan ketika mencoba memprediksi masa depan, seperti moving average, regresi, autoregresi, dll. Pertama, mari kita mulai dengan yang paling sederhana untuk moving average:
movingAverageFunction<- function(data,n=10){ out= data for(i in n:length(data)){ out[i] = mean(data[(i-n+1):i]) } return(out) }
Dalam kode sebelumnya, nilai default untuk jumlah periode adalah 10. Kita bisa menggunakan dataset yang disebut MSFT yang termasuk dalam paket R yang disebut
timeSeries (lihat kode berikut):
library(timeSeries) data(MSFT) p<-MSFT$Close
[1] 60.6250 61.3125 60.3125 59.1250 56.5625 55.4375
head(ma)
[1] 60.62500 61.31250 60.75000 60.25000 58.66667 57.04167
mean(p[1:3])
[1] 60.75
mean(p[2:4])
[1] 60.25
Dalam mode manual, kami menemukan bahwa rata-rata dari tiga nilai pertama
x cocok dengan nilai ketiga
y . Di satu sisi, kita bisa menggunakan rata-rata bergerak untuk memprediksi masa depan.
Dalam contoh berikut, kami akan menunjukkan cara mengevaluasi pengembalian pasar yang diharapkan tahun depan. Di sini kami menggunakan indeks S & P500 dan nilai historis rata-rata tahunan sebagai nilai yang kami harapkan. Beberapa perintah pertama digunakan untuk memuat dataset terkait bernama
.sp500monthly . Tujuan dari program ini adalah untuk menilai rata-rata tahunan rata-rata dan interval kepercayaan 90 persen:
library(data.table) path<-'http://canisius.edu/~yany/RData/' dataSet<-'sp500monthly.RData' link<-paste(path,dataSet,sep='') load(url(link))
[min mean max ]
cat(min2,ourMean,max2,"\n")
0.05032956 0.09022369 0.1301178
Seperti yang Anda lihat dari hasilnya, pengembalian tahunan rata-rata historis untuk S & P500 adalah 9%. Tetapi kami tidak dapat mengatakan bahwa profitabilitas indeks tahun depan akan menjadi 9%, karena bisa dari 5% hingga 13%, dan ini adalah fluktuasi besar.
Musiman
Dalam contoh berikut, kami menunjukkan penggunaan autokorelasi. Pertama, kami mengunduh paket R yang disebut
astsa , yang merupakan kependekan dari analisis deret waktu statistik. Lalu kami memuat PDB AS dengan frekuensi triwulanan:
library(astsa) path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) x<-.usGDPquarterly$DATE y<-.usGDPquarterly$GDP_CURRENT plot(x,y) diff4 = diff(y,4) acf2(diff4,24)
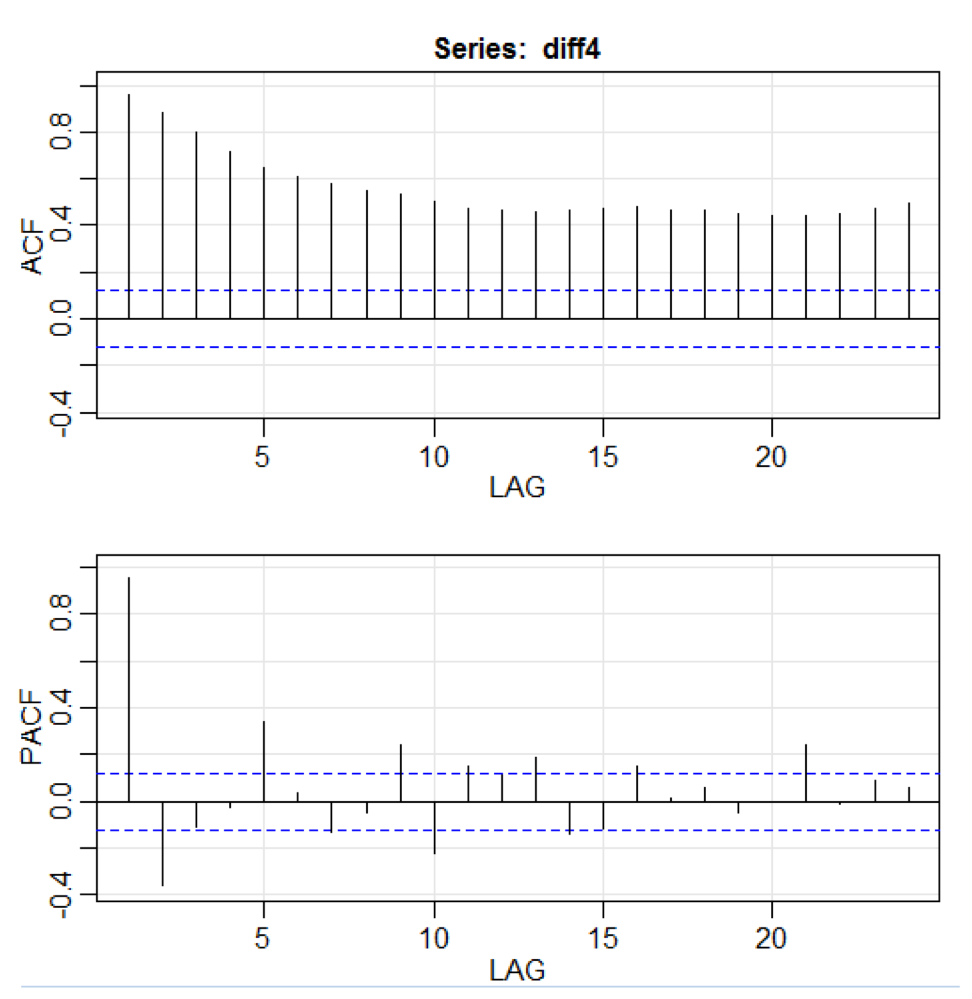
Dalam kode di atas, fungsi
diff () menerima perbedaan, misalnya, nilai saat ini dikurangi nilai sebelumnya. Nilai input kedua menunjukkan penundaan. Fungsi yang disebut
acf2 () digunakan untuk membangun dan mencetak seri waktu ACF dan PACF. ACF adalah singkatan dari fungsi autocovariance, dan PACF adalah singkatan dari autocorrelation function. Grafik yang relevan ditunjukkan di sini:
Visualisasi komponen
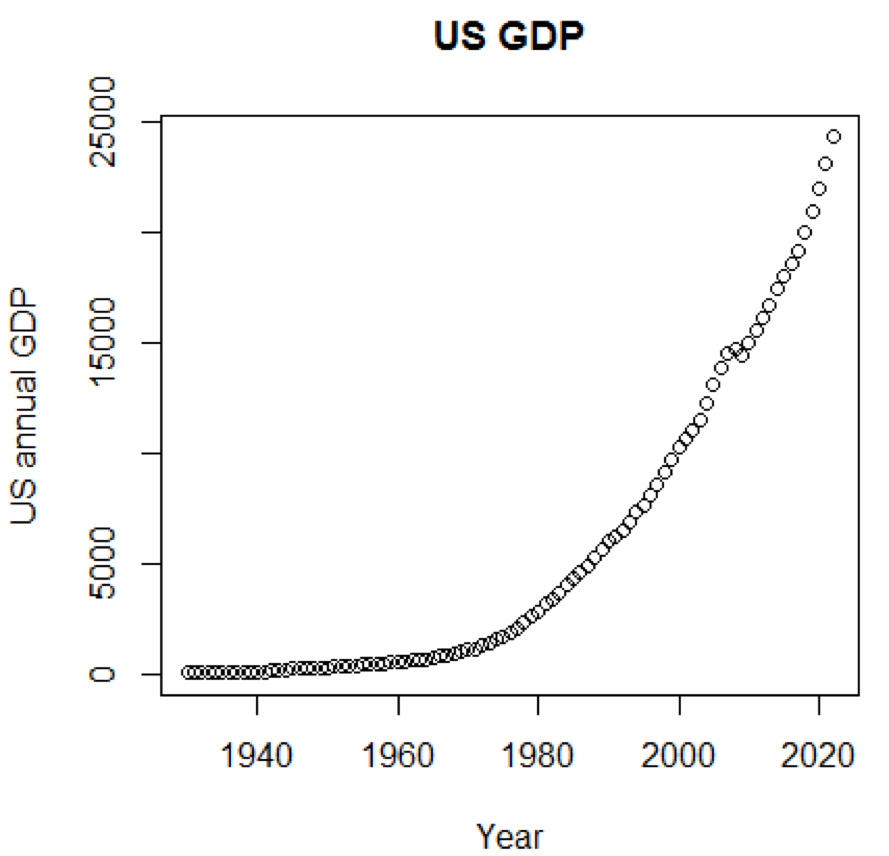
Jelas, konsep dan set data akan jauh lebih dimengerti jika kita bisa menggunakan grafik. Contoh pertama menunjukkan fluktuasi dalam PDB AS selama lima dekade terakhir:
path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) title<-"US GDP" xTitle<-"Year" yTitle<-"US annual GDP" x<-.usGDPannual$YEAR y<-.usGDPannual$GDP plot(x,y,main=title,xlab=xTitle,ylab=yTitle)
Jadwal yang sesuai ditunjukkan di sini:
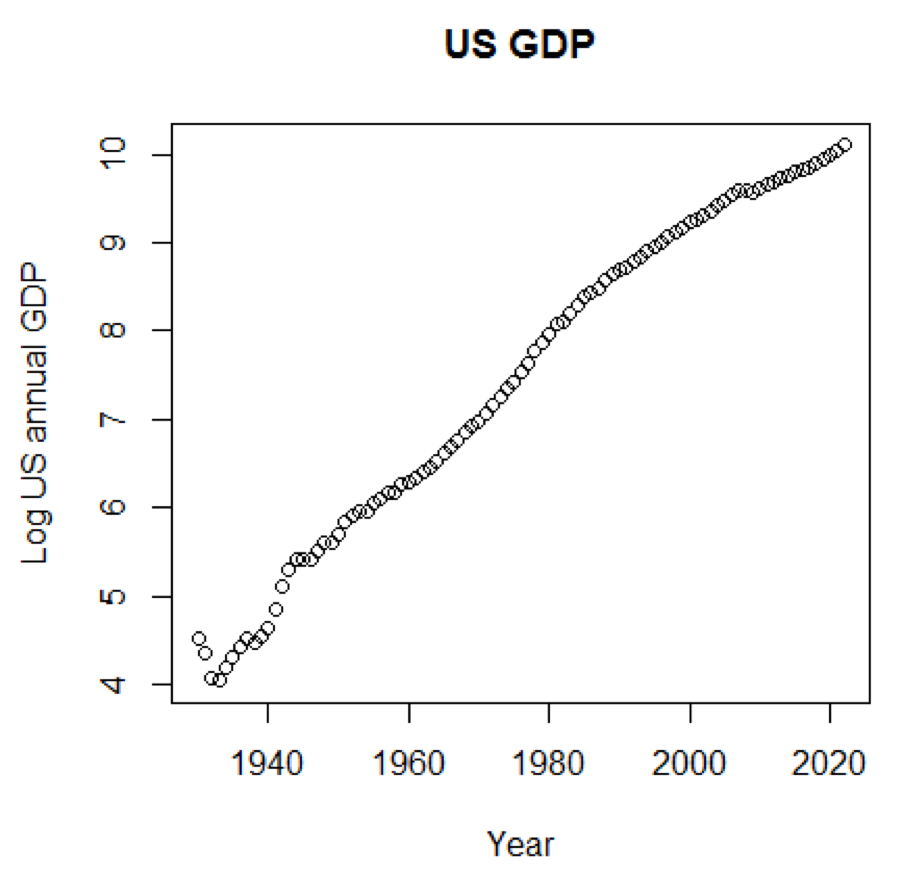
Jika kami menggunakan skala logaritmik untuk PDB, kami akan memiliki kode dan grafik berikut:
yTitle<-"Log US annual GDP" plot(x,log(y),main=title,xlab=xTitle,ylab=yTitle)
Bagan berikut ini dekat dengan garis lurus:
Paket R - LiblineaR
Paket ini adalah model prediksi linier berdasarkan LIBLINEAR C / C ++ Library. Berikut adalah salah satu contoh penggunaan dataset
iris . Program mencoba memprediksi kategori mana yang dimiliki pabrik yang menggunakan data pelatihan:
library(LiblineaR) data(iris) attach(iris) x=iris[,1:4] y=factor(iris[,5]) train=sample(1:dim(iris)[1],100) xTrain=x[train,];xTest=x[-train,] yTrain=y[train]; yTest=y[-train] s=scale(xTrain,center=TRUE,scale=TRUE)
Kesimpulannya adalah sebagai berikut. BCR adalah tingkat klasifikasi yang seimbang. Untuk taruhan ini, semakin tinggi semakin baik:
cat("Best model type is:",bestType,"\n")
Best model type is: 4
cat("Best cost is:",bestCost,"\n")
Best cost is: 1
cat("Best accuracy is:",bestAcc,"\n")
Best accuracy is: 0.98
print(res) yTest setosa versicolor virginica setosa 16 0 0 versicolor 0 17 0 virginica 0 3 14 print(BCR)
[1] 0.95
Paket R - eclust
Paket ini adalah pengelompokan berorientasi menengah untuk model prediksi yang ditafsirkan dalam data dimensi tinggi. Pertama, mari kita lihat kumpulan data yang disebut
simdata yang berisi data simulasi untuk suatu paket:
library(eclust) data("simdata") dim(simdata)
[1] 100 502
simdata[1:5, 1:6]
YE Gene1 Gene2 Gene3 Gene4 [1,] -94.131497 0 -0.4821629 0.1298527 0.4228393 0.36643188 [2,] 7.134990 0 -1.5216289 -0.3304428 -0.4384459 1.57602830 [3,] 1.974194 0 0.7590055 -0.3600983 1.9006443 -1.47250061 [4,] -44.855010 0 0.6833635 1.8051352 0.1527713 -0.06442029 [5,] 23.547378 0 0.4587626 -0.3996984 -0.5727255 -1.75716775
table(simdata[,"E"])
0 1 50 50
Kesimpulan sebelumnya menunjukkan bahwa dimensi data adalah 100 kali 502.
Y adalah vektor respons kontinu, dan
E adalah variabel lingkungan biner untuk metode ECLUST.
E = 0 untuk tidak terpapar (n = 50) dan
E = 1 untuk terpapar (n = 50).
Program R berikut mengevaluasi Fisher z-transform:
library(eclust) data("simdata") X = simdata[,c(-1,-2)] firstCorr<-cor(X[1:50,]) secondCorr<-cor(X[51:100,]) score<-u_fisherZ(n0=100,cor0=firstCorr,n1=100,cor1=secondCorr) dim(score)
[1] 500 500
score[1:5,1:5]
Gene1 Gene2 Gene3 Gene4 Gene5 Gene1 1.000000 -8.062020 6.260050 -8.133437 -7.825391 Gene2 -8.062020 1.000000 9.162208 -7.431822 -7.814067 Gene3 6.260050 9.162208 1.000000 8.072412 6.529433 Gene4 -8.133437 -7.431822 8.072412 1.000000 -5.099261 Gene5 -7.825391 -7.814067 6.529433 -5.099261 1.000000
Kami mendefinisikan Fisher z-transform. Dengan asumsi bahwa kita memiliki seperangkat
n pasangan
x i dan
y i , kita dapat memperkirakan korelasinya menggunakan rumus berikut:
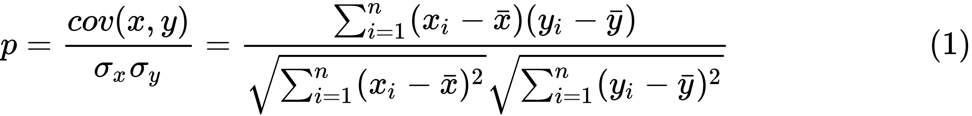
Di sini
p adalah korelasi antara dua variabel, dan

dan
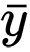
adalah alat sampel untuk variabel acak
x dan
y . Nilai
z didefinisikan sebagai:
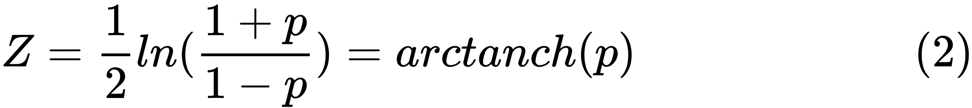 Ini
Ini adalah fungsi logaritma natural, dan
arctanh () adalah fungsi tangen hiperbolik terbalik.
Pemilihan model
Saat menemukan model yang baik, terkadang kita dihadapkan pada kekurangan / kelebihan data. Contoh berikut dipinjam
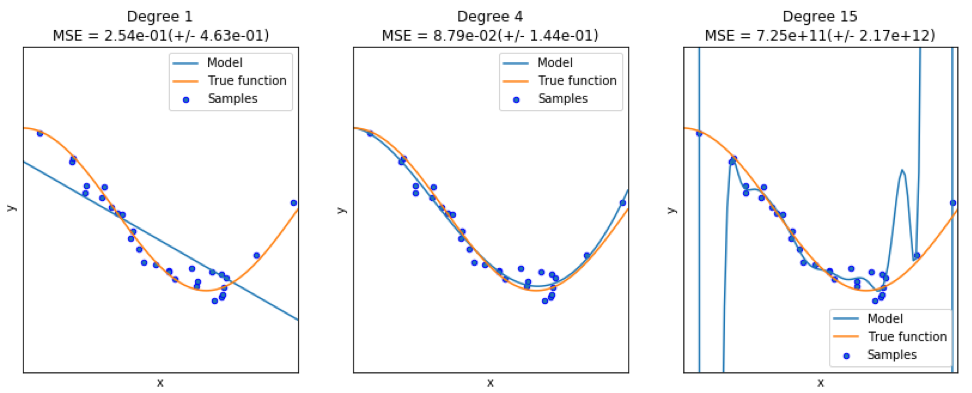
dari sini . Ini menunjukkan masalah bekerja dengan ini dan bagaimana kita dapat menggunakan regresi linier dengan fitur polinomial untuk memperkirakan fungsi-fungsi non-linear. Fungsi yang ditentukan:
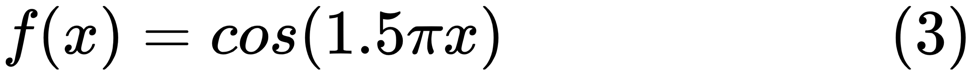
Dalam program selanjutnya, kami mencoba menggunakan model linear dan polinomial untuk memperkirakan persamaan. Kode yang sedikit dimodifikasi ditampilkan di sini. Program ini menggambarkan efek dari kekurangan / kelebihan data pada model:
import sklearn import numpy as np import matplotlib.pyplot as plt from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression from sklearn.model_selection import cross_val_score
Grafik yang dihasilkan ditunjukkan di sini:
Paket python - model-catwalk
Contohnya dapat ditemukan di
sini .
Beberapa baris kode pertama ditampilkan di sini:
import datetime import pandas from sqlalchemy import create_engine from metta import metta_io as metta from catwalk.storage import FSModelStorageEngine, CSVMatrixStore from catwalk.model_trainers import ModelTrainer from catwalk.predictors import Predictor from catwalk.evaluation import ModelEvaluator from catwalk.utils import save_experiment_and_get_hash help(FSModelStorageEngine)
Kesimpulan yang sesuai ditunjukkan di sini. Untuk menghemat ruang, hanya bagian atas yang disajikan:
Help on class FSModelStorageEngine in module catwalk.storage: class FSModelStorageEngine(ModelStorageEngine) | Method resolution order: | FSModelStorageEngine | ModelStorageEngine | builtins.object | | Methods defined here: | | __init__(self, *args, **kwargs) | Initialize self. See help(type(self)) for accurate signature. | | get_store(self, model_hash) | | ----------------------------------------------------------------------
| Data descriptors inherited from ModelStorageEngine: | | __dict__ | dictionary for instance variables (if defined) | | __weakref__ | list of weak references to the object (if defined)
Paket python - sklearn
Karena
sklearn adalah paket yang sangat berguna, ada baiknya menunjukkan lebih banyak contoh penggunaan paket ini. Contoh yang diberikan di sini menunjukkan cara menggunakan paket untuk mengklasifikasikan dokumen berdasarkan topik menggunakan pendekatan bag-of-words.
Contoh ini menggunakan matriks
scipy.sparse untuk menyimpan objek dan menunjukkan berbagai pengklasifikasi yang secara efisien dapat memproses matriks jarang. Contoh ini menggunakan dataset 20 newsgroup. Ini akan diunduh secara otomatis dan kemudian di-cache. File zip berisi file input dan dapat diunduh di
sini . Kode tersedia di
sini . Untuk menghemat ruang, hanya beberapa baris pertama yang ditampilkan:
import logging import numpy as np from optparse import OptionParser import sys from time import time import matplotlib.pyplot as plt from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.feature_extraction.text import HashingVectorizer from sklearn.feature_selection import SelectFromModel
Output yang sesuai ditunjukkan di sini:
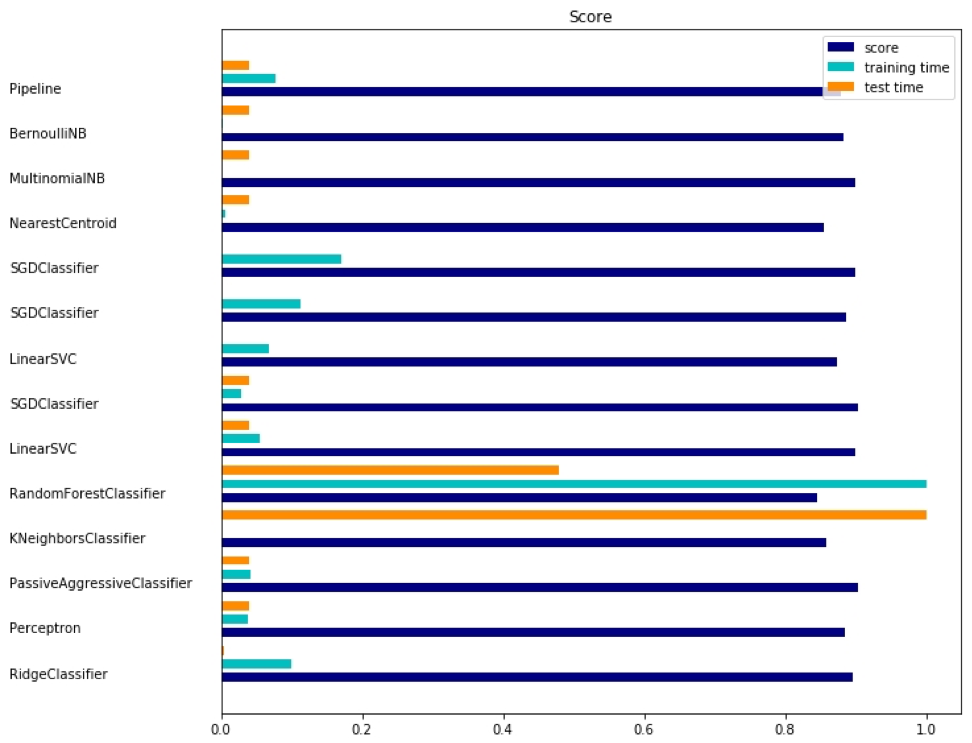
Ada tiga indikator untuk setiap metode: penilaian, waktu pelatihan dan waktu pengujian.
Paket Julia - QuantEcon
Ambil contoh, penggunaan rantai Markov:
using QuantEcon P = [0.4 0.6; 0.2 0.8]; mc = MarkovChain(P) x = simulate(mc, 100000); mean(x .== 1)
Hasil:
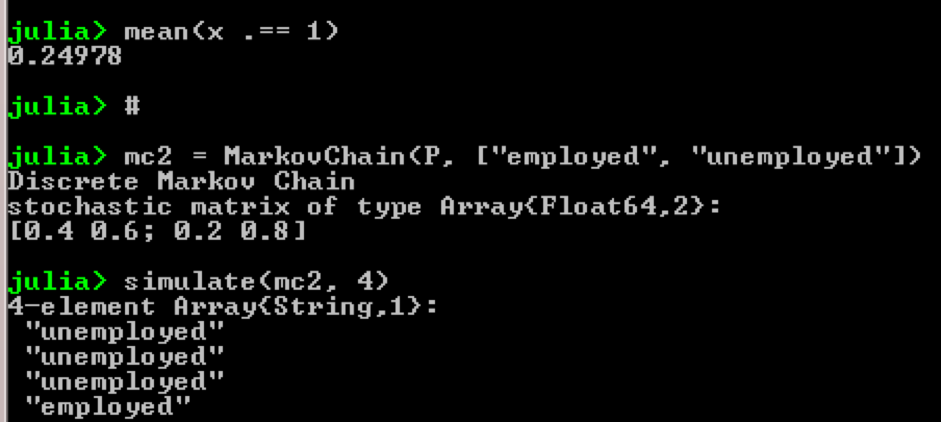
Tujuan dari contoh ini adalah untuk melihat bagaimana seseorang dari satu status ekonomi di masa depan berubah menjadi orang lain. Pertama, mari kita lihat tabel berikut:
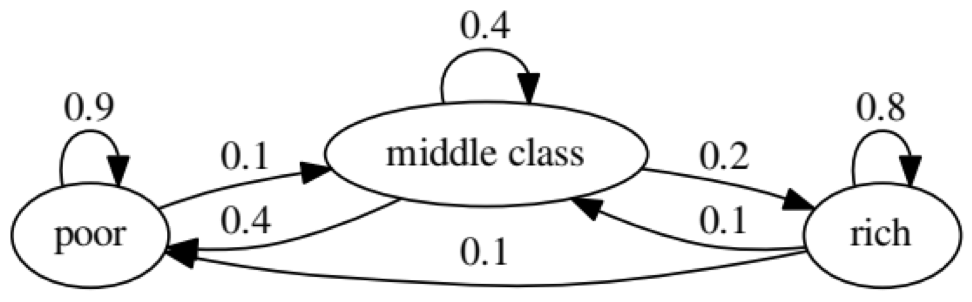
Mari kita lihat oval paling kiri dengan status "buruk". 0,9 berarti bahwa seseorang dengan status ini memiliki peluang 90% untuk tetap miskin, dan 10% masuk ke kelas menengah. Itu dapat diwakili oleh matriks berikut, nol adalah di mana tidak ada tepi antara node:
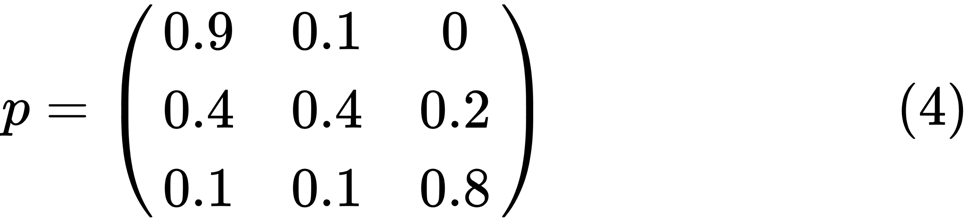
Dikatakan bahwa dua keadaan, x dan y, saling terkait jika ada bilangan bulat positif j dan k, seperti:

Rantai Markov
P disebut irreducible jika semua negara terhubung; yaitu, jika
x dan
y dilaporkan untuk masing-masing (x, y). Kode berikut akan mengkonfirmasi ini:
using QuantEcon P = [0.9 0.1 0.0; 0.4 0.4 0.2; 0.1 0.1 0.8]; mc = MarkovChain(P) is_irreducible(mc)
Grafik berikut menunjukkan kasus yang ekstrem, karena status orang miskin di masa mendatang adalah 100% miskin:

Kode berikut juga akan mengkonfirmasi ini, karena hasilnya akan
salah :
using QuantEcon P2 = [1.0 0.0 0.0; 0.1 0.8 0.1; 0.0 0.2 0.8]; mc2 = MarkovChain(P2) is_irreducible(mc2)
Uji Kausalitas Granger
Uji kausalitas Granger digunakan untuk menentukan apakah satu rangkaian waktu merupakan faktor dan memberikan informasi yang berguna untuk memprediksi yang kedua. Kode berikut menggunakan
dataset bernama
ChickEgg sebagai ilustrasi. Kumpulan data memiliki dua kolom, jumlah ayam dan jumlah telur, dengan cap waktu:
library(lmtest) data(ChickEgg) dim(ChickEgg)
[1] 54 2
ChickEgg[1:5,]
chicken egg [1,] 468491 3581 [2,] 449743 3532 [3,] 436815 3327 [4,] 444523 3255 [5,] 433937 3156
Pertanyaannya adalah, dapatkah kita menggunakan jumlah telur tahun ini untuk memprediksi jumlah ayam tahun depan?
Jika demikian, maka jumlah ayam akan menjadi alasan Granger untuk jumlah telur. Jika ini bukan masalahnya, kami katakan bahwa jumlah ayam bukan alasan Granger untuk jumlah telur. Ini kode yang relevan:
library(lmtest) data(ChickEgg) grangertest(chicken~egg, order = 3, data = ChickEgg)
Granger causality test Model 1: chicken ~ Lags(chicken, 1:3) + Lags(egg, 1:3) Model 2: chicken ~ Lags(chicken, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 5.405 0.002966 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Pada model 1, kami mencoba menggunakan lag ayam ditambah lag telur untuk menjelaskan jumlah anak ayam.
Karena nilai
P cukup kecil (signifikan pada 0,01), kami mengatakan bahwa jumlah telur adalah alasan Granger untuk jumlah ayam.
Tes berikut menunjukkan bahwa data pada ayam tidak dapat digunakan untuk memprediksi periode berikut:
grangertest(egg~chicken, order = 3, data = ChickEgg)
Granger causality test Model 1: egg ~ Lags(egg, 1:3) + Lags(chicken, 1:3) Model 2: egg ~ Lags(egg, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 0.5916 0.6238
Dalam contoh berikut, kami memeriksa profitabilitas IBM dan S & P500 untuk mengetahui bahwa mereka adalah alasan Granger untuk yang lain.
Pertama, kami mendefinisikan fungsi hasil:
ret_f<-function(x,ticker=""){ n<-nrow(x) p<-x[,6] ret<-p[2:n]/p[1:(n-1)]-1 output<-data.frame(x[2:n,1],ret) name<-paste("RET_",toupper(ticker),sep='') colnames(output)<-c("DATE",name) return(output) }
>x<-read.csv("http://canisius.edu/~yany/data/ibmDaily.csv",header=T) ibmRet<-ret_f(x,"ibm") x<-read.csv("http://canisius.edu/~yany/data/^gspcDaily.csv",header=T) mktRet<-ret_f(x,"mkt") final<-merge(ibmRet,mktRet) head(final)
DATE RET_IBM RET_MKT 1 1962-01-03 0.008742545 0.0023956877 2 1962-01-04 -0.009965497 -0.0068887673 3 1962-01-05 -0.019694350 -0.0138730891 4 1962-01-08 -0.018750380 -0.0077519519 5 1962-01-09 0.011829467 0.0004340133 6 1962-01-10 0.001798526 -0.0027476933
Sekarang fungsi dapat dipanggil dengan nilai input. Tujuan dari program ini adalah untuk menguji apakah kita dapat menggunakan jeda pasar untuk menjelaskan keuntungan IBM. Dengan cara yang sama, kami memeriksa untuk menjelaskan keterlambatan pendapatan pasar IBM:
library(lmtest) grangertest(RET_IBM ~ RET_MKT, order = 1, data =final)
Granger causality test Model 1: RET_IBM ~ Lags(RET_IBM, 1:1) + Lags(RET_MKT, 1:1) Model 2: RET_IBM ~ Lags(RET_IBM, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 24.002 9.729e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Hasil menunjukkan bahwa S & P500 dapat digunakan untuk menjelaskan profitabilitas IBM untuk periode berikutnya, karena secara statistik signifikan pada 0,1%. Kode berikut akan memeriksa untuk melihat apakah kelambatan IBM menjelaskan perubahan dalam S & P500:
grangertest(RET_MKT ~ RET_IBM, order = 1, data =final)
Granger causality test Model 1: RET_MKT ~ Lags(RET_MKT, 1:1) + Lags(RET_IBM, 1:1) Model 2: RET_MKT ~ Lags(RET_MKT, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 7.5378 0.006049 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Hasilnya menunjukkan bahwa selama periode ini, pengembalian IBM dapat digunakan untuk menjelaskan indeks S & P500 untuk periode berikutnya.