Kata Pengantar

Pada artikel ini, kita akan mengeksplorasi beberapa aspek SVM:
- komponen teoritis SVM;
- bagaimana algoritma bekerja pada sampel yang tidak dapat dibagi ke dalam kelas secara linear;
- Contoh python dan implementasi algoritma di pustaka Belajar SciKit.
Dalam artikel berikut, saya akan mencoba untuk berbicara tentang komponen matematika dari algoritma ini.
Seperti yang Anda ketahui, tugas pembelajaran mesin dibagi menjadi dua kategori utama - klasifikasi dan regresi. Bergantung pada tugas mana yang kita hadapi, dan dataset mana yang kita miliki untuk tugas ini, kita memilih algoritma mana yang akan digunakan.
Metode Mesin Vektor Pendukung atau SVM (dari Mesin Vektor Dukungan Bahasa Inggris) adalah algoritma linier yang digunakan dalam masalah klasifikasi dan regresi. Algoritma ini banyak digunakan dalam praktik dan dapat memecahkan masalah linier dan nonlinier. Inti dari "Mesin" dari Vektor Pendukung adalah sederhana: algoritma membuat garis atau hyperplane yang membagi data ke dalam kelas.
Teori
Tugas utama dari algoritma adalah untuk menemukan garis yang paling benar, atau hyperplane, membagi data menjadi dua kelas. SVM adalah algoritma yang menerima data pada input dan mengembalikan garis pemisah tersebut.
Perhatikan contoh berikut. Misalkan kita memiliki kumpulan data, dan kita ingin mengklasifikasikan dan memisahkan kotak merah dari lingkaran biru (katakanlah positif dan negatif). Tujuan utama dalam tugas ini adalah menemukan garis "ideal" yang akan memisahkan kedua kelas ini.
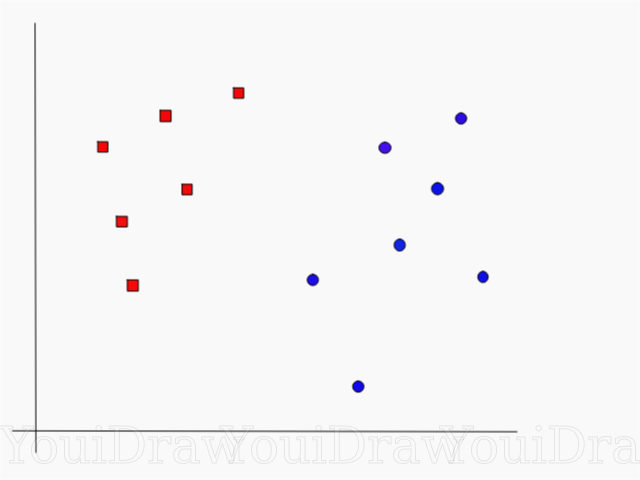
Temukan garis sempurna, atau hyperplane, yang membagi kumpulan data menjadi kelas biru dan merah.
Sepintas, itu tidak terlalu sulit, bukan?
Tapi, seperti yang Anda lihat, tidak ada satu pun, garis unik, yang akan menyelesaikan masalah seperti itu. Kita dapat mengambil jumlah baris yang tak terbatas yang dapat memisahkan kedua kelas ini. Bagaimana tepatnya SVM menemukan garis "ideal", dan apa yang "ideal" dalam pemahamannya?
Lihatlah contoh di bawah ini dan pikirkan yang mana dari dua garis (kuning atau hijau) yang paling memisahkan kedua kelas, dan cocok dengan deskripsi "ideal"?
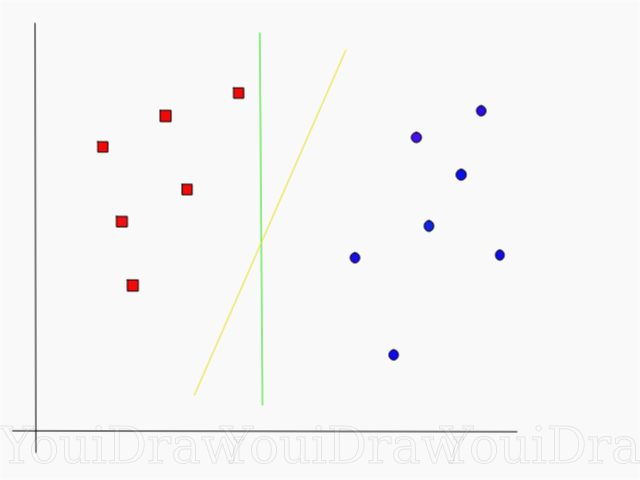
Baris mana yang lebih baik memisahkan dataset menurut pendapat Anda?
Jika Anda memilih garis kuning, saya mengucapkan selamat kepada Anda: ini adalah garis yang akan dipilih algoritma. Dalam contoh ini, kita dapat secara intuitif memahami bahwa garis kuning memisahkan dan karenanya mengklasifikasikan dua kelas lebih baik daripada yang hijau.
Dalam kasus garis hijau - terletak terlalu dekat dengan kelas merah. Terlepas dari kenyataan bahwa ia dengan benar mengklasifikasikan semua objek dari set data saat ini, garis seperti itu tidak akan digeneralisasi - itu tidak akan berperilaku sama baiknya dengan set data yang tidak dikenal. Tugas menemukan dua kelas yang digeneralisasi secara umum adalah salah satu tugas utama dalam pembelajaran mesin.
Bagaimana SVM Menemukan Jalur Terbaik
Algoritma SVM dirancang sedemikian rupa sehingga mencari titik-titik pada grafik yang terletak langsung ke garis pemisahan terdekat. Titik-titik ini disebut vektor referensi. Kemudian, algoritma menghitung jarak antara vektor dukungan dan bidang pembagi. Ini adalah jarak yang disebut celah. Tujuan utama dari algoritma ini adalah untuk memaksimalkan jarak clearance. Hyperplane terbaik dianggap sebagai hyperplane yang celahnya sebesar mungkin.

Cukup sederhana, bukan? Pertimbangkan contoh berikut, dengan dataset yang lebih kompleks yang tidak dapat dibagi secara linear.
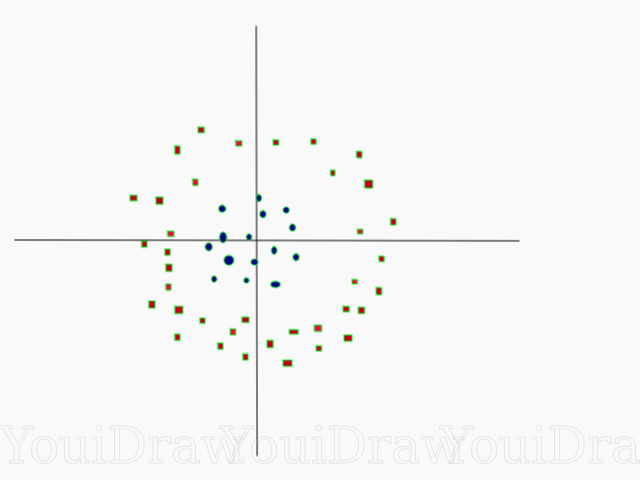
Jelas, dataset ini tidak dapat dibagi secara linear. Kami tidak dapat menggambar garis lurus yang akan mengklasifikasikan data ini. Namun, dataset ini dapat dibagi secara linear, menambahkan dimensi tambahan, yang akan kita sebut sumbu Z. Bayangkan bahwa koordinat pada sumbu Z diatur oleh batasan berikut:
Dengan demikian, ordinat Z diwakili dari kuadrat jarak titik ke awal sumbu.
Di bawah ini adalah visualisasi dari dataset yang sama pada sumbu Z.
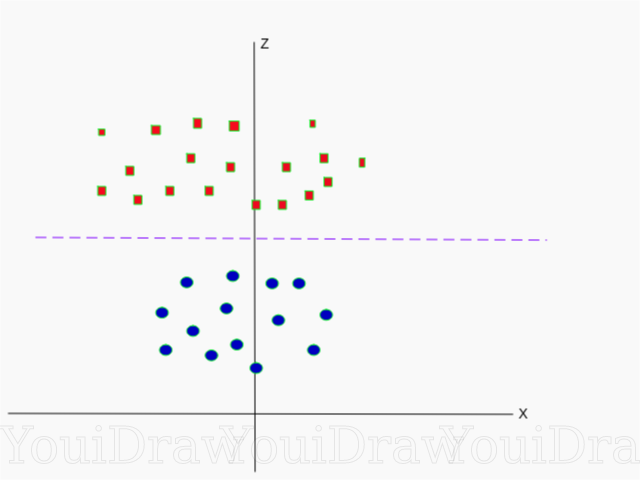
Sekarang data dapat dibagi secara linear. Misalkan garis magenta memisahkan data z = k, di mana k adalah konstanta. Jika
lalu
- rumus lingkaran. Jadi, kita dapat memproyeksikan pembagi linier kita, kembali ke jumlah asli dimensi sampel, menggunakan transformasi ini.
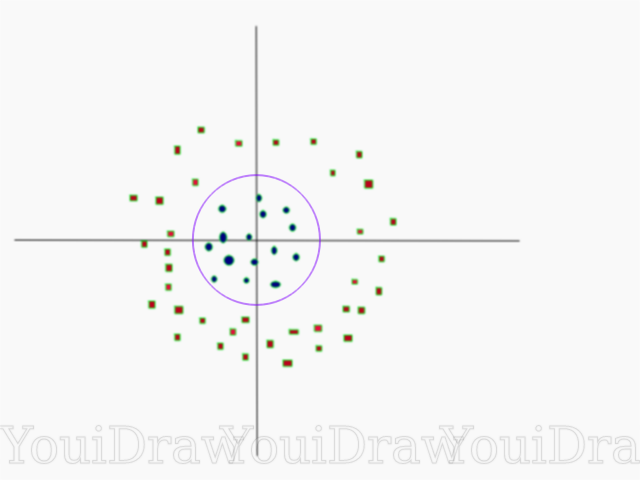
Sebagai hasilnya, kita dapat mengklasifikasikan kumpulan data non-linear dengan menambahkan dimensi tambahan untuknya, dan kemudian membawanya kembali ke bentuk aslinya menggunakan transformasi matematika. Namun, tidak dengan semua kumpulan data, transformasi yang demikian mudah dilakukan. Untungnya, implementasi algoritma ini di pustaka sklearn memecahkan masalah ini bagi kami.
Hyperplane
Sekarang kita telah membiasakan diri dengan logika algoritma, kita beralih ke definisi formal hyperplane
Hyperplane adalah subplane n-1 dimensi dalam ruang Euclidean n-dimensi yang membagi ruang menjadi dua bagian terpisah.
Misalnya, bayangkan garis kami direpresentasikan sebagai ruang Euclidean satu dimensi (yaitu kumpulan data kami terletak pada garis lurus). Pilih satu titik di baris ini. Titik ini akan membagi kumpulan data, dalam kasus kami garis, menjadi dua bagian. Garis memiliki satu ukuran, dan titik tersebut memiliki 0 ukuran. Oleh karena itu, sebuah titik adalah hyperplane dari sebuah garis.
Untuk dataset dua dimensi yang kami temui sebelumnya, garis pemisah adalah hyperplane yang sama. Sederhananya, untuk ruang n-dimensi ada hyperplane n-1 dimensi yang membagi ruang ini menjadi dua bagian.
Kode
import numpy as np X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) y = np.array([1, 1, 2, 2])
Poin direpresentasikan sebagai larik X, dan kelas-kelas tempat mereka termasuk larik y.
Sekarang kita akan melatih model kita dengan sampel ini. Untuk contoh ini, saya mengatur parameter linear "kernel" dari classifier (kernel).
from sklearn.svm import SVC clf = SVC(kernel='linear') clf = SVC.fit(X, y)
Prediksi kelas objek baru
prediction = clf.predict([[0,6]])
Pengaturan Parameter
Parameter adalah argumen yang Anda berikan saat membuat classifier. Di bawah ini saya telah memberikan beberapa pengaturan SVM khusus yang paling penting:
"C"Parameter ini membantu untuk menyesuaikan garis halus antara "kehalusan" dan keakuratan klasifikasi objek dalam sampel pelatihan. Semakin tinggi nilai "C", semakin banyak objek dalam set pelatihan yang akan diklasifikasikan dengan benar.

Dalam contoh ini, ada beberapa ambang keputusan yang dapat kita tentukan untuk sampel khusus ini. Perhatikan ambang keputusan langsung (disajikan pada grafik sebagai garis hijau). Ini cukup sederhana, dan karena alasan ini, beberapa objek diklasifikasikan secara salah. Poin-poin ini yang telah diklasifikasikan secara salah disebut outlier dalam data.
Kami juga dapat menyesuaikan parameter sedemikian rupa sehingga pada akhirnya kami mendapatkan garis yang lebih melengkung (ambang keputusan biru muda), yang akan mengklasifikasikan secara mutlak semua data sampel pelatihan dengan benar. Tentu saja, dalam hal ini, kemungkinan bahwa model kami akan dapat menggeneralisasi dan menunjukkan hasil yang sama baiknya pada data baru sangat kecil. Karena itu, jika Anda berusaha mencapai akurasi saat melatih model, Anda harus membidik sesuatu yang lebih rata, langsung. Semakin tinggi angka "C", semakin terjerat hyperplane akan ada dalam model Anda, tetapi semakin tinggi jumlah objek yang diklasifikasikan dengan benar dalam set pelatihan. Oleh karena itu, penting untuk "memutar" parameter model untuk set data tertentu untuk menghindari pelatihan ulang tetapi, pada saat yang sama, mencapai akurasi tinggi.
GammaDalam dokumentasi resmi, pustaka Belajar SciKit mengatakan bahwa gamma menentukan seberapa jauh masing-masing elemen dalam kumpulan data memiliki pengaruh dalam menentukan “garis ideal”. Semakin rendah gamma, semakin banyak elemen, bahkan yang cukup jauh dari garis pemisah, ikut serta dalam proses pemilihan garis ini. Jika gamma tinggi, maka algoritma akan "bergantung" hanya pada elemen-elemen yang paling dekat dengan garis itu sendiri.
Jika level gamma diatur terlalu tinggi, maka hanya elemen yang paling dekat dengan garis yang akan berpartisipasi dalam proses pengambilan keputusan di lokasi garis. Ini akan membantu untuk mengabaikan pencilan dalam data. Algoritma SVM dirancang sedemikian rupa sehingga titik-titik yang terletak paling dekat satu sama lain memiliki bobot lebih saat membuat keputusan. Namun, dengan pengaturan yang benar untuk "C" dan "gamma", hasil optimal dapat dicapai yang membangun hyperplane yang lebih linier yang mengabaikan outlier dan, oleh karena itu, lebih dapat digeneralisasikan.
Kesimpulan
Saya sangat berharap artikel ini membantu Anda memahami esensi karya SVM atau Metode Vektor Referensi. Saya mengharapkan dari Anda setiap komentar dan saran. Dalam publikasi berikutnya, saya akan berbicara tentang komponen matematika dari SVM dan masalah optimisasi.
Sumber:
Dokumentasi SVM Resmi di SciKit LearnMenuju Blog DataSiraj Raval: Mendukung Mesin VektorPengantar Mesin Belajar Udacity SVM: Video kursus GammaWikipedia: SVM