Sumber : Lisensi Wikipedia CC-BY-SA 3.0

Jika Anda sering bepergian dengan transportasi umum, Anda mungkin menemukan situasi ini:

Anda berhenti. Ada tertulis bahwa bus beroperasi setiap 10 menit. Catat waktu ... Akhirnya, setelah 11 menit, bus tiba dan pikiran: mengapa saya selalu sial?

Secara teori, jika bus tiba setiap 10 menit, dan Anda tiba secara acak, maka rata-rata penantiannya sekitar 5 menit. Namun dalam kenyataannya, bus tidak tiba sesuai jadwal, sehingga Anda bisa menunggu lebih lama. Ternyata, dengan beberapa asumsi yang masuk akal, seseorang dapat sampai pada kesimpulan yang mengejutkan:

Saat menunggu bus yang tiba rata-rata setiap 10 menit, waktu tunggu rata-rata Anda adalah 10 menit.

Inilah yang kadang-kadang disebut paradoks waktu tunggu .

Saya punya ide sebelumnya, dan saya selalu bertanya-tanya apakah ini benar ... berapa banyak "asumsi masuk akal" sesuai dengan kenyataan? Dalam artikel ini, kami memeriksa paradoks latensi dalam hal pemodelan dan argumen probabilistik, dan kemudian melihat beberapa data bus Seattle nyata untuk (mudah-mudahan) menyelesaikan paradoks sekali dan untuk semua.

Inspeksi paradoks

Jika bus tiba tepat setiap sepuluh menit, maka waktu tunggu rata-rata adalah 5 menit. Orang dapat dengan mudah memahami mengapa menambahkan variasi pada interval antara bus meningkatkan waktu tunggu rata-rata.

Paradoks waktu tunggu adalah kasus khusus dari fenomena yang lebih umum - paradoks inspeksi , yang dibahas secara rinci dalam artikel Allen Downey yang masuk akal, "Paradoks Inspeksi Di Mana Saja Di Sekitar Kita . "

Singkatnya, paradoks inspeksi muncul setiap kali probabilitas mengamati kuantitas terkait dengan kuantitas yang diamati. Allen memberikan contoh survei mahasiswa tentang ukuran rata-rata kelas mereka. Meskipun sekolah secara jujur berbicara tentang jumlah rata-rata 30 siswa dalam suatu kelompok, ukuran kelompok rata-rata dari sudut pandang siswa jauh lebih besar. Alasannya adalah bahwa di kelas besar (secara alami) ada lebih banyak siswa, yang terungkap selama survei mereka.

Dalam hal jadwal bus dengan interval dinyatakan 10 menit, kadang-kadang interval antara kedatangan lebih dari 10 menit, dan kadang-kadang lebih pendek. Dan jika Anda berhenti pada waktu yang acak, maka Anda lebih mungkin menghadapi interval yang lebih lama daripada yang lebih pendek. Dan oleh karena itu logis bahwa interval waktu rata-rata antara interval menunggu lebih lama daripada interval waktu rata-rata antara bus, karena interval yang lebih lama lebih umum dalam sampel.

Tetapi paradoks latensi membuat pernyataan yang lebih kuat: jika jarak bus rata-rata adalah

$N$ menit, waktu tunggu rata-rata untuk penumpang adalah

$2N$ menit. Mungkinkah ini benar?

Simulasi latensi

Untuk meyakinkan diri kita tentang kewajaran ini, pertama-tama kita mensimulasikan arus bus yang tiba dalam rata-rata 10 menit. Untuk akurasi, ambil sampel besar: satu juta bus (atau sekitar 10 tahun lalu lintas 10 menit setiap hari):

import numpy as np N = 1000000 # number of buses tau = 10 # average minutes between arrivals rand = np.random.RandomState(42) # universal random seed bus_arrival_times = N * tau * np.sort(rand.rand(N))

Pastikan interval rata-rata dekat

$\ tau = 10$ :

 intervals = np.diff(bus_arrival_times) intervals.mean()

9.9999879601518398

Sekarang kita dapat mensimulasikan kedatangan sejumlah besar penumpang di halte selama periode waktu ini dan menghitung waktu tunggu yang mereka alami masing-masing. Enkapsulasi kode dalam fungsi untuk digunakan nanti:

 def simulate_wait_times(arrival_times, rseed=8675309, # Jenny's random seed n_passengers=1000000): rand = np.random.RandomState(rseed) arrival_times = np.asarray(arrival_times) passenger_times = arrival_times.max() * rand.rand(n_passengers) # find the index of the next bus for each simulated passenger i = np.searchsorted(arrival_times, passenger_times, side='right') return arrival_times[i] - passenger_times

Kemudian kami mensimulasikan waktu tunggu dan menghitung rata-rata:

 wait_times = simulate_wait_times(bus_arrival_times) wait_times.mean()

10.001584206227317

Waktu tunggu rata-rata mendekati 10 menit, seperti yang diprediksikan oleh paradoks.

Menggali lebih dalam: probabilitas dan proses Poisson

Bagaimana cara mensimulasikan situasi seperti itu?

Bahkan, ini adalah contoh dari paradoks inspeksi, di mana probabilitas mengamati nilai terkait dengan nilai itu sendiri. Ditunjukkan oleh

$p (T)$ jarak

$T$ antar bus saat mereka tiba di halte bus. Dalam catatan seperti itu, nilai yang diharapkan dari waktu kedatangan adalah:

$E [T] = \ int_0 ^ \ infty T ~ p (T) ~ dT$

Dalam simulasi sebelumnya, kami memilih

$E [T] = \ tau = 10$ menit.

Ketika seorang penumpang tiba di halte kapan saja, kemungkinan waktu menunggu tidak hanya bergantung pada

$p (T)$ tetapi juga dari

$T$ : semakin besar interval, semakin banyak penumpang di dalamnya.

Dengan demikian, kita dapat menulis distribusi waktu kedatangan dari sudut pandang penumpang:

$p_ {exp} (T) \ propto T ~ p (T)$

Konstanta proporsionalitas diperoleh dari normalisasi distribusi:

$p_ {exp} (T) = \ frac {T ~ p (T)} {\ int_0 ^ \ infty T ~ p (T) ~ dT}$

Menyederhanakan

$p_ {exp} (T) = \ frac {T ~ p (T)} {E [T]}$

Maka waktu tunggu

$E [W]$ akan menjadi setengah dari interval yang diharapkan untuk penumpang, sehingga kami dapat merekam

$E [W] = \ frac {1} {2} E_ {exp} [T] = \ frac {1} {2} \ int_0 ^ \ infty T ~ p_ {exp} (T) ~ dT$

yang dapat ditulis ulang dengan cara yang lebih dimengerti:

$E [W] = \ frac {E [T ^ 2]} {2E [T]}$

dan sekarang tinggal memilih formulir saja

$p (T)$ dan menghitung integral.

Pilihan p (T)

Setelah menerima model formal, untuk apa distribusi yang masuk akal

$p (T)$ ? Kami akan menggambar distribusi

$p (T)$ dalam kedatangan yang disimulasikan dengan memplot histogram interval antara kedatangan:

 %matplotlib inline import matplotlib.pyplot as plt plt.style.use('seaborn') plt.hist(intervals, bins=np.arange(80), density=True) plt.axvline(intervals.mean(), color='black', linestyle='dotted') plt.xlabel('Interval between arrivals (minutes)') plt.ylabel('Probability density');

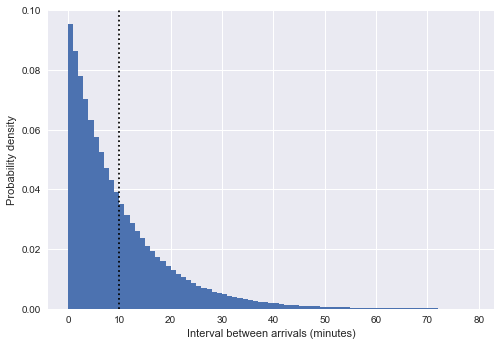
Di sini, garis putus-putus vertikal menunjukkan interval rata-rata sekitar 10 menit. Ini sangat mirip dengan distribusi eksponensial, dan bukan secara tidak sengaja: simulasi kami tentang waktu kedatangan bus dalam bentuk angka acak seragam sangat dekat dengan proses Poisson , dan untuk proses seperti itu, distribusi interval bersifat eksponensial.

(Catatan: dalam kasus kami, ini hanya perkiraan eksponen; pada kenyataannya, intervalnya)

$T$ antara

$N$ poin yang dipilih secara merata dalam rentang waktu

$N \ tau$ cocok dengan distribusi beta

$T / (N \ tau) \ sim \ mathrm {Beta} [1, N]$ yang ada dalam batas besar

$N$ mendekati

$T \ sim \ mathrm {Exp} [1 / \ tau]$ . Untuk informasi lebih lanjut, Anda dapat membaca, misalnya, sebuah posting di StackExchange atau utas ini di Twitter ).

Distribusi interval eksponensial menyiratkan bahwa waktu kedatangan mengikuti proses Poisson. Untuk memverifikasi alasan ini, kami memeriksa keberadaan properti lain dari proses Poisson: bahwa jumlah kedatangan selama periode waktu tertentu adalah distribusi Poisson. Untuk melakukan ini, kami membagi kedatangan yang disimulasikan menjadi blok waktu:

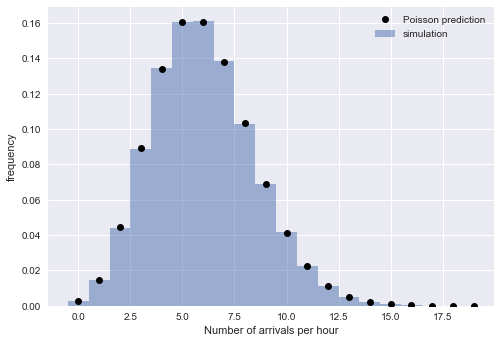
 from scipy.stats import poisson # count the number of arrivals in 1-hour bins binsize = 60 binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int)) x = np.arange(20) # plot the results plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation') plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction') plt.xlabel('Number of arrivals per hour') plt.ylabel('frequency') plt.legend();

Korespondensi erat dari nilai-nilai empiris dan teoritis meyakinkan kita tentang kebenaran interpretasi kita: untuk besar

$N$ Waktu kedatangan yang disimulasikan dijelaskan dengan baik oleh proses Poisson, yang menyiratkan interval terdistribusi secara eksponensial.

Ini berarti bahwa distribusi probabilitas dapat ditulis:

$p (T) = \ frac {1} {\ tau} e ^ {- T / \ tau}$

Jika kami mengganti hasilnya dengan formula sebelumnya, kami akan menemukan rata-rata waktu tunggu penumpang di halte:

$E [W] = \ frac {\ int_0 ^ \ infty T ^ 2 ~ e ^ {- T / \ tau}} {2 \ int_0 ^ \ infty T ~ e ^ {- T / \ tau}} = \ frac {2 \ tau ^ 3} {2 (\ tau ^ 2)} = \ tau$

Untuk penerbangan dengan kedatangan melalui proses Poisson, waktu tunggu yang diharapkan identik dengan interval rata-rata antara kedatangan.

Masalah ini dapat diperdebatkan sebagai berikut: proses Poisson adalah proses tanpa ingatan , yaitu, sejarah peristiwa tidak ada hubungannya dengan waktu yang diharapkan dari peristiwa berikutnya. Oleh karena itu, pada saat kedatangan di halte, waktu tunggu rata-rata untuk sebuah bus selalu sama: dalam kasus kami, itu adalah 10 menit, terlepas dari berapa banyak waktu yang telah berlalu sejak bus sebelumnya! Tidak masalah berapa lama Anda telah menunggu: waktu yang diharapkan untuk bus berikutnya selalu tepat 10 menit: dalam proses Poisson Anda tidak mendapatkan "kredit" untuk waktu yang dihabiskan menunggu.

Batas waktu realitas

Di atas bagus jika kedatangan bus sebenarnya dijelaskan oleh proses Poisson, tapi benarkah begitu?

Sumber: Skema Transportasi Umum Seattle

Mari kita coba menentukan bagaimana paradoks waktu tunggu itu konsisten dengan kenyataan. Untuk melakukan ini, kami akan memeriksa beberapa data yang tersedia untuk diunduh di sini: arrival_times.csv (file 3 MB CSV). Dataset berisi waktu kedatangan yang direncanakan dan aktual untuk bus RapidRide C, D, dan E di Halte Bus ke-3 & Pike di pusat kota Seattle. Data ini direkam pada kuartal kedua 2016 (terima kasih banyak kepada Mark Hallenback dari Washington State Transportation Center untuk file ini!).

 import pandas as pd df = pd.read_csv('arrival_times.csv') df = df.dropna(axis=0, how='any') df.head()

	OPD_DATE	VEHICLE_ID	RTE	DIR	TRIP_ID	STOP_ID	STOP_NAME	SCH_STOP_TM	ACT_STOP_TM
0	2016-03-26	6201	673	S	30908177	431	3RD AVE & PIKE ST (431)	01:11:57	01:13:19
1	2016-03-26	6201	673	S	30908033	431	3RD AVE & PIKE ST (431)	23:19:57	23:16:13
2	2016-03-26	6201	673	S	30908028	431	3RD AVE & PIKE ST (431)	21:19:57	21:18:46
3	2016-03-26	6201	673	S	30908019	431	3RD AVE & PIKE ST (431)	19:04:57	19:01:49
4	2016-03-26	6201	673	S	30908252	431	3RD AVE & PIKE ST (431)	16:42:57	16:42:39

Saya memilih data RapidRide, termasuk karena untuk sebagian besar hari bus berjalan secara berkala 10-15 menit, belum lagi fakta bahwa saya sering menjadi penumpang rute C.

Pembersihan data

Pertama, kami akan melakukan sedikit pembersihan data untuk mengubahnya menjadi tampilan yang nyaman:

 # combine date and time into a single timestamp df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM']) df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM']) # if scheduled & actual span midnight, then the actual day needs to be adjusted minute = np.timedelta64(1, 'm') hour = 60 * minute diff_hrs = (df['actual'] - df['scheduled']) / hour df.loc[diff_hrs > 20, 'actual'] -= 24 * hour df.loc[diff_hrs < -20, 'actual'] += 24 * hour df['minutes_late'] = (df['actual'] - df['scheduled']) / minute # map internal route codes to external route letters df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category') df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category') # extract useful columns df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy() df.head()

	Rute	Arahan	Grafik	Fakta kedatangan	Keterlambatan (min)
0	C	selatan	2016-03-26 01:11:57	2016-03-26 01:13:19	1.366667
1	C	selatan	2016-03-26 23:19:57	2016-03-26 23:16:13	-3.733333
2	C	selatan	2016-03-26 21:19:57	2016-03-26 21:18:46	-1.183333
3	C	selatan	2016-03-26 19:04:57	2016-03-26 19:01:49	-3.133333
4	C	selatan	2016-03-26 16:42:57	2016-03-26 16:42:39	-0.300000

Sampai jam berapa bus?

Ada enam set data dalam tabel ini: arah utara dan selatan untuk setiap rute C, D dan E. Untuk mendapatkan gambaran tentang karakteristiknya, mari kita buat histogram dari aktual dikurangi waktu kedatangan yang direncanakan untuk masing-masing dari enam ini:

 import seaborn as sns g = sns.FacetGrid(df, row="direction", col="route") g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20)) g.set_titles('{col_name} {row_name}') g.set_axis_labels('minutes late', 'number of buses');

Adalah logis untuk mengasumsikan bahwa bus lebih dekat dengan jadwal di awal rute dan menyimpang lebih banyak dari itu menjelang akhir. Data mengkonfirmasi ini: pemberhentian kami di rute selatan C, serta di utara D dan E dekat dengan awal rute, dan di arah yang berlawanan, tidak jauh dari tujuan akhir.

Interval yang dijadwalkan dan diamati

Lihatlah interval bus yang diamati dan direncanakan untuk enam rute ini. Mari kita mulai dengan fungsi groupby di Pandas untuk menghitung interval ini:

 def compute_headway(scheduled): minute = np.timedelta64(1, 'm') return scheduled.sort_values().diff() / minute grouped = df.groupby(['route', 'direction']) df['actual_interval'] = grouped['actual'].transform(compute_headway) df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway)

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('actual interval (minutes)', 'number of buses');

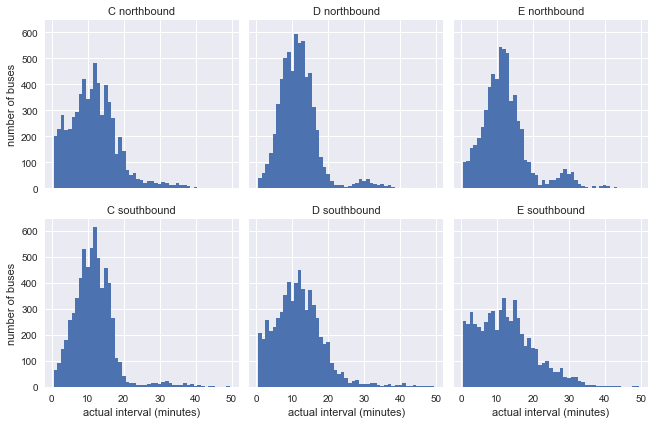
Sudah jelas bahwa hasilnya tidak sangat mirip dengan distribusi eksponensial dari model kami, tetapi ini masih tidak mengatakan apa-apa: distribusi dapat dipengaruhi oleh interval yang tidak konsisten dalam grafik.

Mari kita ulangi konstruksi diagram, dengan mengambil interval yang direncanakan, daripada interval kedatangan yang diamati:

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('scheduled interval (minutes)', 'frequency');

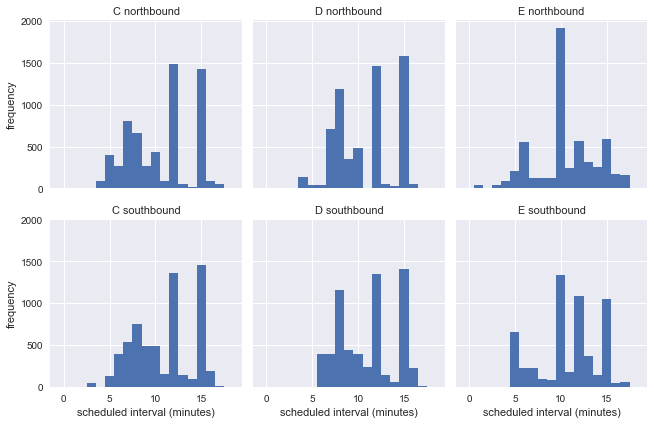
Ini menunjukkan bahwa selama minggu ini bus beroperasi pada interval yang berbeda, sehingga kami tidak dapat memperkirakan akurasi paradoks waktu tunggu menggunakan informasi nyata dari halte bus.

Membuat jadwal seragam

Meskipun jadwal resmi tidak memberikan interval yang seragam, ada beberapa interval waktu tertentu dengan sejumlah besar bus: misalnya, hampir 2000 bus rute E ke utara dengan interval yang direncanakan 10 menit. Untuk mengetahui apakah paradoks latensi berlaku, mari kelompokkan data menjadi rute, arah, dan interval yang direncanakan, lalu susun kembali seolah-olah telah terjadi secara berurutan. Ini harus menjaga semua karakteristik yang relevan dari data sumber, sambil memfasilitasi perbandingan langsung dengan prediksi paradoks latensi.

 def stack_sequence(data): # first, sort by scheduled time data = data.sort_values('scheduled') # re-stack data & recompute relevant quantities data['scheduled'] = data['scheduled_interval'].cumsum() data['actual'] = data['scheduled'] + data['minutes_late'] data['actual_interval'] = data['actual'].sort_values().diff() return data subset = df[df.scheduled_interval.isin([10, 12, 15])] grouped = subset.groupby(['route', 'direction', 'scheduled_interval']) sequenced = grouped.apply(stack_sequence).reset_index(drop=True) sequenced.head()

	Rute	Arahan	Jadwalkan	Fakta kedatangan	Keterlambatan (min)	Fakta interval	Interval Terjadwal
0	C	utara	10.0	12.400000	2.400.000	NaN	10.0
1	C	utara	20.0	27.150000	7.150000	0,183333	10.0
2	C	utara	30.0	26.966667	-3.033333	14.566667	10.0
3	C	utara	40.0	35.516667	-4,483333	8.366667	10.0
4	C	utara	50.0	53.583333	3.583333	18.066667	10.0

Pada data yang dibersihkan, Anda dapat membuat grafik distribusi tampilan aktual bus di sepanjang setiap rute dan arah dengan frekuensi kedatangan:

 for route in ['C', 'D', 'E']: g = sns.FacetGrid(sequenced.query(f"route == '{route}'"), row="direction", col="scheduled_interval") g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5) g.set_titles('{row_name} ({col_name:.0f} min)') g.set_axis_labels('actual interval (min)', 'count') g.fig.set_size_inches(8, 4) g.fig.suptitle(f'{route} line', y=1.05, fontsize=14)

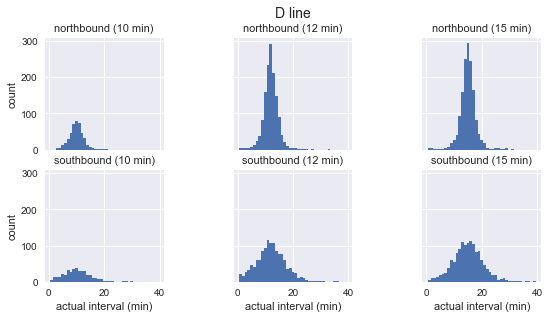
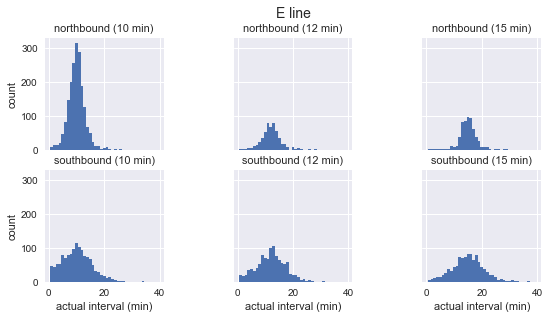
Kita melihat bahwa untuk setiap rute distribusi interval yang diamati hampir Gaussian. Ini puncak dekat interval yang direncanakan dan memiliki standar deviasi yang kurang pada awal rute (selatan untuk C, utara untuk D / E) dan lebih banyak di akhir. Bahkan secara kasat mata, interval kedatangan aktual jelas tidak sesuai dengan distribusi eksponensial, yang merupakan asumsi utama yang menjadi dasar paradoks waktu tunggu.

Kita dapat mengambil fungsi simulasi waktu tunggu yang kami gunakan di atas untuk menemukan rata-rata waktu tunggu untuk setiap rute bus, arah dan jadwal:

 grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval']) sims = grouped['actual'].apply(simulate_wait_times) sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std()))

  Rute Rute, Jadwal Terjadwal
 C utara 10.0 7.8 +/- 12.5
                       12.0 7.4 +/- 5.7
                       15.0 8.8 +/- 6.4
          selatan 10.0 6.2 +/- 6.3
                       12.0 6.8 +/- 5.2
                       15.0 8.4 +/- 7.3
 D utara 10.0 6.1 +/- 7.1
                       12.0 6.5 +/- 4.6
                       15.0 7.9 +/- 5.3
          selatan 10.0 6.7 +/- 5.3
                       12.0 7.5 +/- 5.9
                       15.0 8.8 +/- 6.5
 E utara 10.0 5.5 +/- 3.7
                       12.0 6.5 +/- 4.3
                       15.0 7.9 +/- 4.9
          selatan 10.0 6.8 +/- 5.6
                       12.0 7.3 +/- 5.2
                       15.0 8.7 +/- 6.0
 Nama: aktual, dtype: objek

Rata-rata waktu tunggu, mungkin satu atau dua menit, lebih dari setengah interval yang direncanakan, tetapi tidak sama dengan interval yang direncanakan, seperti yang disiratkan oleh paradoks waktu tunggu. Dengan kata lain, paradoks inspeksi dikonfirmasi, tetapi paradoks waktu tunggu tidak benar.

Kesimpulan

Paradoks latensi adalah titik awal yang menarik untuk diskusi yang mencakup pemodelan, teori probabilitas, dan membandingkan asumsi statistik dengan kenyataan. Meskipun kami telah mengkonfirmasi bahwa di dunia nyata, rute bus mematuhi semacam paradoks inspeksi, analisis di atas menunjukkan cukup meyakinkan: asumsi utama yang mendasari paradoks waktu tunggu - bahwa kedatangan bus mengikuti statistik proses Poisson - tidak dibenarkan.

Dalam retrospeksi, ini tidak mengejutkan: proses Poisson adalah proses tanpa memori yang mengasumsikan bahwa probabilitas kedatangan sepenuhnya independen dari waktu sejak kedatangan sebelumnya. Bahkan, sistem transportasi umum yang dikelola dengan baik memiliki jadwal yang terstruktur khusus untuk menghindari perilaku ini: bus tidak memulai rute mereka secara acak pada siang hari, tetapi mulai sesuai dengan jadwal yang dipilih untuk transportasi penumpang yang paling efisien.

Pelajaran yang lebih penting adalah berhati-hati dengan asumsi yang Anda buat tentang tugas analisis data apa pun. Terkadang proses Poisson adalah deskripsi yang baik untuk data waktu kedatangan. Tetapi hanya karena satu tipe data terdengar seperti tipe data lain tidak berarti bahwa asumsi yang diizinkan untuk satu data tentu valid untuk yang lainnya. Seringkali asumsi yang tampaknya benar dapat mengarah pada kesimpulan yang tidak benar.

Paradoks waktu menunggu, atau mengapa bus saya selalu terlambat?