Setahun setengah yang lalu, saya menerbitkan artikel "Matematika pada Fingers: Least Square Methods" , yang menerima respons yang sangat baik, yang, antara lain, terdiri atas fakta bahwa saya mengusulkan menggambar burung hantu. Nah, karena burung hantu, maka Anda perlu menjelaskannya lagi. Dalam seminggu, tepatnya tentang hal ini, saya akan mulai memberikan beberapa kuliah kepada mahasiswa geologi; Saya mengambil kesempatan ini, saya menyajikan di sini poin utama (diadaptasi) sebagai konsep. Tujuan utama saya bukan untuk memberikan resep yang sudah jadi dari buku tentang makanan enak dan sehat, tetapi untuk menjelaskan mengapa begitu dan apa lagi yang ada di bagian yang sesuai, karena koneksi antara berbagai bagian matematika adalah yang paling menarik!

Saat ini, saya bermaksud untuk memecah teks sebagai berikut:

• Program pendidikan tentang teori probabilitas (artikel pengantar, opsional)
  
• Pengantar sistem persamaan linear
  
• Metode elemen hingga
  
• Minimalisasi bentuk kuadratik dan contoh masalah OLS
  
• Dari Kotak Terkecil ke Jaringan Saraf Tiruan
  

Saya akan pergi ke kotak paling sedikit sedikit ke samping, melalui prinsip kemungkinan maksimum, dan itu membutuhkan orientasi minimal dalam teori probabilitas. Teks ini dirancang untuk tahun ketiga fakultas geologi kami, yang berarti (dari sudut pandang peralatan yang terlibat!) Bahwa siswa sekolah menengah yang tertarik dengan semangat yang sesuai harus dapat memahaminya.

Bagaimana suara sang teoretis atau apakah Anda percaya pada teori evolusi?

Suatu hari saya ditanya apakah saya percaya pada teori evolusi. Diam sekarang, pikirkan bagaimana Anda akan menjawabnya.



Secara pribadi, saya terkejut, menjawab bahwa saya merasa itu dapat dipercaya, dan bahwa pertanyaan tentang iman tidak muncul sama sekali di sini. Teori ilmiah tidak ada hubungannya dengan iman. Singkatnya, teorinya hanya membangun model dunia di sekitar kita, tidak perlu untuk mempercayainya. Selain itu, kriteria Popper membutuhkan teori ilmiah untuk dapat membantah. Dan juga teori yang sehat harus memiliki, pertama-tama, kekuatan prediksi. Misalnya, jika Anda memodifikasi tanaman secara genetis sedemikian rupa sehingga mereka sendiri menghasilkan pestisida, masuk akal jika serangga yang kebal terhadap mereka akan muncul. Namun, secara signifikan kurang jelas bahwa proses ini dapat diperlambat dengan menanam tanaman biasa berdampingan dengan yang dimodifikasi secara genetik. Berdasarkan teori evolusi, simulasi yang sesuai membuat prediksi seperti itu , dan tampaknya dikonfirmasi .

Dan apa hubungannya dengan kotak terkecil?

Seperti yang saya sebutkan sebelumnya, saya akan pergi ke kuadrat terkecil melalui prinsip kemungkinan maksimum. Mari kita ilustrasikan dengan sebuah contoh. Misalkan kita tertarik pada data tentang pertumbuhan penguin, tetapi kita hanya dapat mengukur beberapa burung yang indah ini. Sangat logis untuk memperkenalkan model distribusi pertumbuhan ke dalam tugas - paling sering itu normal. Distribusi normal ditandai oleh dua parameter - nilai rata-rata dan standar deviasi. Untuk setiap nilai tetap dari parameter, kita dapat menghitung probabilitas bahwa pengukuran yang kita buat akan dihasilkan. Selanjutnya, dengan memvariasikan parameter, kami menemukan parameter yang memaksimalkan probabilitas.

Jadi, untuk bekerja dengan kemungkinan maksimum, kita perlu beroperasi dalam hal teori probabilitas. Sedikit lebih rendah, di jari, kita mendefinisikan konsep probabilitas dan kemungkinan, tetapi pertama-tama saya ingin fokus pada aspek lain. Secara mengejutkan saya jarang melihat orang berpikir tentang kata "teori" dalam frasa "teori probabilitas".

Apa yang dipelajari theorver?

Mengenai asal-usul, makna, dan ruang lingkup perkiraan probabilitas, perdebatan sengit telah berlangsung selama lebih dari seratus tahun. Misalnya, Bruno De Finetti menyatakan bahwa probabilitas tidak lebih dari analisis subjektif dari kemungkinan bahwa sesuatu akan terjadi, dan bahwa probabilitas ini tidak ada di luar pikiran. Ini adalah kesediaan seseorang untuk bertaruh pada sesuatu yang terjadi. Pendapat ini secara langsung berlawanan dengan pandangan klasik / freventists pada probabilitas hasil tertentu dari suatu peristiwa, di mana ia diasumsikan bahwa peristiwa yang sama dapat diulang beberapa kali, dan "probabilitas" dari hasil tertentu terkait dengan frekuensi hasil tertentu yang jatuh selama tes berulang. Selain subjektivis dan freventis, ada juga objektivisme yang berpendapat bahwa probabilitas adalah aspek nyata dari alam semesta, dan bukan hanya deskripsi tingkat kepercayaan pengamat.

Meskipun demikian, tetapi ketiga mazhab ilmiah dalam praktiknya menggunakan alat yang sama berdasarkan aksioma Kolmogorov. Mari kita memberikan argumen tidak langsung, dari sudut pandang subjektivisme, yang mendukung teori probabilitas, dibangun di atas aksioma Kolmogorov. Kami memberikan aksioma sendiri sesaat kemudian, tetapi untuk permulaan kami akan menganggap bahwa kami memiliki taruhan yang akan menerima taruhan pada Piala Dunia berikutnya. Mari kita memiliki dua acara: a = tim Uruguay akan menjadi juara, b = tim Jerman akan menjadi juara. Taruhan memperkirakan peluang tim Uruguay untuk menang di 40%, peluang tim Jerman di 30%. Jelas, Jerman dan Uruguay tidak bisa menang pada saat yang sama, oleh karena itu peluang a∧b adalah nol. Nah, pada saat yang sama, taruhan yakin bahwa kemungkinan Uruguay atau Jerman (dan bukan Argentina atau Australia) akan menang adalah 80%. Mari kita tulis dalam bentuk berikut:



Jika taruhan menyatakan bahwa tingkat kepercayaannya pada acara a adalah 0,4, yaitu, P (a) = 0,4, maka pemain dapat memilih apakah ia akan bertaruh untuk atau menentang mengatakan, jumlah taruhan yang kompatibel dengan tingkat kepercayaan taruhan. Ini berarti bahwa pemain dapat bertaruh bahwa acara akan terjadi dengan bertaruh empat rubel melawan enam rubel taruhan. Atau seorang pemain dapat bertaruh enam rubel alih-alih empat rubel taruhan yang tidak akan terjadi.

Jika tingkat kepercayaan dari bandar taruhan tidak secara akurat mencerminkan keadaan dunia, maka kita dapat mengandalkan fakta bahwa dalam jangka panjang itu akan kehilangan uang bagi pemain yang kepercayaannya lebih akurat. Selain itu, dalam contoh khusus ini, pemain memiliki strategi di mana taruhan selalu kehilangan uang. Mari kita ilustrasikan:



Pemain membuat tiga taruhan, dan apa pun hasil kejuaraan, dia selalu menang. Harap dicatat bahwa pertimbangan kemenangan pada prinsipnya tidak termasuk apakah Uruguay atau Jerman adalah favorit kejuaraan, kehilangan taruhan dijamin! Situasi ini dipimpin oleh fakta bahwa taruhan tidak dibimbing oleh dasar-dasar teori probabilitas, setelah melanggar aksioma ketiga Kolmogorov, mari kita bawa ketiganya:



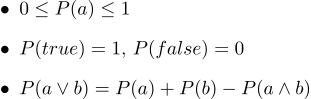
Dalam bentuk teks, mereka terlihat seperti ini:

• 1. Semua probabilitas berkisar dari 0 hingga 1
• 2. Tentu saja, pernyataan benar memiliki probabilitas 1, dan tentu saja probabilitas salah 0.
• 3. Aksioma ketiga adalah aksioma disjungsi, mudah dipahami secara intuitif, mencatat bahwa kasus-kasus di mana pernyataan a benar, bersama dengan kasus-kasus di mana b benar, tentu mencakup semua kasus di mana pernyataan a∨b benar; tetapi dalam jumlah dua set kasus, persimpangan mereka terjadi dua kali, oleh karena itu, perlu untuk mengurangi P (a∧b).

Pada tahun 1931, de Finetti membuktikan pernyataan yang sangat kuat:

Jika taruhan dipandu oleh berbagai tingkat kepercayaan, yang melanggar aksioma teori probabilitas, maka ada kombinasi taruhan pemain yang menjamin hilangnya taruhan (pemain menang) di setiap taruhan.

Aksioma probabilitas dapat dianggap sebagai membatasi seperangkat keyakinan probabilistik yang dimiliki beberapa agen. Harap dicatat bahwa mengikuti taruhan tidak menyiratkan aksioma Kolmogorov bahwa ia akan menang (kami akan mengesampingkan masalah komisi), tetapi jika Anda tidak mengikuti mereka, ia akan dijamin akan kalah. Perhatikan bahwa argumen lain telah diajukan dalam mendukung penerapan probabilitas; tetapi keberhasilan praktis dari sistem penalaran berdasarkan teori probabilitas yang ternyata menjadi insentif yang menarik yang menyebabkan revisi banyak pandangan.

Jadi, kami sedikit membuka tabir mengapa Theorver mungkin masuk akal, tetapi benda apa yang dimanipulasi? Seluruh teori dibangun di atas tiga aksioma; ketiganya melibatkan beberapa fungsi sihir P. Terlebih lagi, melihat aksioma-aksioma ini, sangat mengingatkan saya pada fungsi area bentuk. Mari kita coba untuk melihat apakah area tersebut berfungsi untuk menentukan probabilitas.

Kami mendefinisikan kata "event" sebagai "subset dari unit square". Kami mendefinisikan kata "probabilitas suatu peristiwa" sebagai "area dari subset yang sesuai." Secara kasar, kami memiliki target kardus besar, dan kami, setelah menutup mata, menembaknya. Peluang peluru jatuh ke dalam set yang diberikan berbanding lurus dengan area set. Peristiwa yang dapat diandalkan dalam kasus ini adalah seluruh kotak, dan jelas salah, misalnya, setiap titik dari kotak. Ini mengikuti dari definisi kita tentang probabilitas bahwa tidak mungkin mencapai titik dengan sempurna (peluru kita adalah titik material). Saya sangat suka gambar, dan saya menggambar banyak dari mereka, dan theorver tidak terkecuali! Mari kita ilustrasikan ketiga aksioma:



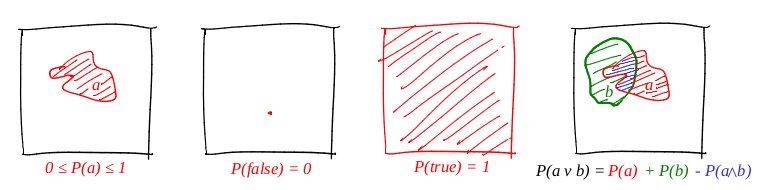
Jadi, aksioma pertama terpenuhi: daerah tersebut tidak negatif, dan tidak dapat melebihi satuan. Peristiwa yang dapat diandalkan adalah seluruh kotak, dan yang sengaja salah adalah rangkaian nol area. Dan itu berfungsi sempurna dengan disjunct!

Kredibilitas Maksimum dengan Contoh

Contoh Satu: Balik Koin

Mari kita lihat contoh sederhana dari lemparan koin, alias skema Bernoulli . N percobaan dilakukan, di mana masing-masing satu dari dua peristiwa dapat terjadi ("sukses" atau "gagal"), satu dengan probabilitas p , dan yang kedua dengan probabilitas 1-p . Tugas kita adalah menemukan probabilitas untuk mendapatkan keberhasilan yang tepat dalam percobaan ini. Peluang ini memberi kita rumus Bernoulli:



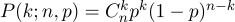
Ambil koin biasa ( p = 0,5 ), lemparkan sepuluh kali ( n = 10 ), dan pertimbangkan berapa kali ekornya dijatuhkan:



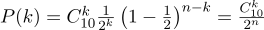
Berikut ini adalah grafik kepadatan probabilitas:



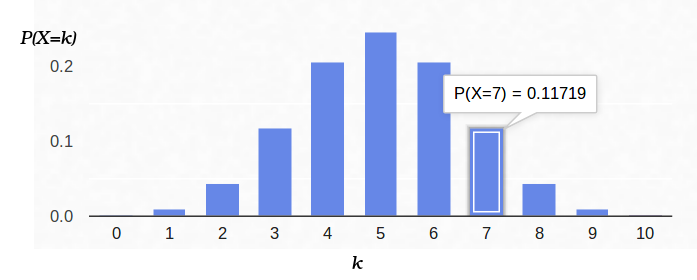
Jadi, jika kita memperbaiki probabilitas timbulnya "sukses" (0,5), dan juga mencatat jumlah percobaan (10), maka jumlah kemungkinan "keberhasilan" dapat berupa bilangan bulat antara 0 dan 10, namun, hasil ini tidak mungkin sama kemungkinannya. Jelas bahwa mendapatkan lima "keberhasilan" jauh lebih mungkin daripada tidak satu pun. Sebagai contoh, probabilitas menghitung tujuh ekor adalah sekitar 12%.

Sekarang mari kita lihat tugas yang sama dari sisi lain. Kami memiliki koin nyata, tetapi kami tidak tahu distribusi probabilitas "sukses" / "kegagalan". Namun, kita dapat membuangnya sepuluh kali dan menghitung jumlah "keberhasilan". Sebagai contoh, kami memiliki tujuh ekor. Bagaimana ini membantu kami mengevaluasi hal ?

Kita dapat mencoba memperbaiki n = 10 dan k = 7 dalam rumus Bernoulli, meninggalkan p parameter gratis:



Maka rumus Bernoulli dapat ditafsirkan sebagai kemungkinan parameter yang diestimasi, (dalam hal ini, p ). Saya bahkan mengubah huruf fungsi, sekarang L (dari bahasa Inggris). Artinya, kemungkinan adalah kemungkinan menghasilkan data pengamatan (7 ekor dari 10 percobaan) untuk nilai parameter yang diberikan.

Misalnya, kemungkinan koin seimbang ( p = 0,5), asalkan terjadi tujuh dari sepuluh lemparan, adalah sekitar 12%. Anda dapat memplot fungsi L :



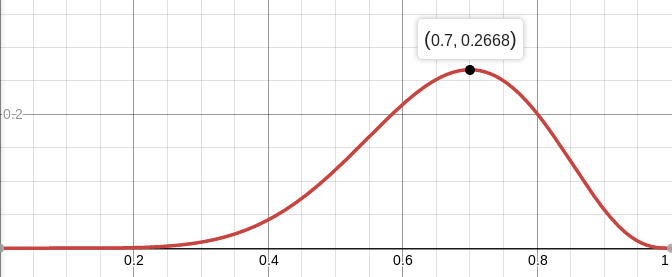
Jadi, kami mencari nilai parameter yang memaksimalkan kemungkinan mendapatkan pengamatan yang kami miliki. Dalam kasus khusus ini, kami memiliki fungsi satu variabel, kami sedang mencari yang maksimal. Untuk mempermudah pencarian, saya akan mencari maksimum bukan L , tetapi log L. Logaritma adalah fungsi yang sangat monoton, sehingga memaksimalkan satu dan yang lainnya adalah hal yang persis sama. Dan logaritma memecah produk menjadi jumlah yang jauh lebih nyaman untuk dibedakan. Jadi, kami mencari fungsi maksimum ini:



Untuk melakukan ini, kami menyamakan turunannya dengan nol:



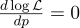
Turunan dari log x = 1 / x, kami memperoleh:



Artinya, kemungkinan maksimum (sekitar 27%) tercapai pada



Untuk berjaga-jaga, kami menghitung turunan kedua:



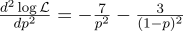
Pada titik p = 0,7, itu negatif, jadi titik ini benar-benar maksimum dari fungsi L.



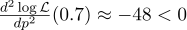
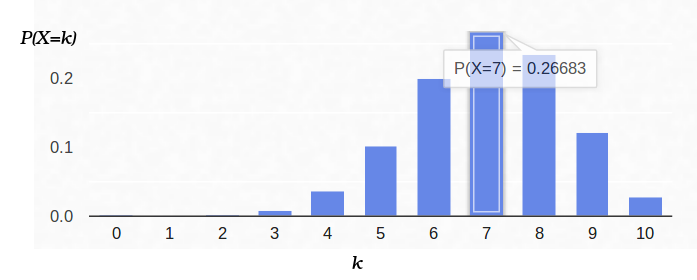
Dan inilah kepadatan probabilitas untuk skema Bernoulli dengan p = 0,7:

Contoh Dua: ADC

Mari kita bayangkan bahwa kita memiliki kuantitas fisik konstan tertentu yang ingin kita ukur, baik itu panjang dengan penggaris atau tegangan dengan voltmeter. Pengukuran apa pun memberikan perkiraan kuantitas ini, tetapi bukan kuantitas itu sendiri. Metode yang saya jelaskan di sini dikembangkan oleh Gauss pada akhir abad ke-18, ketika ia mengukur orbit benda langit.

Sebagai contoh, jika kita mengukur tegangan baterai N kali, kita mendapatkan N pengukuran yang berbeda. Yang mana yang harus diambil? Itu saja! Jadi, mari kita memiliki jumlah N Uj:



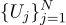
Misalkan setiap pengukuran Uj sama dengan nilai ideal, ditambah noise Gaussian, yang dicirikan oleh dua parameter - posisi bel Gaussian dan "lebarnya". Berikut adalah kepadatan probabilitas:



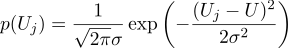
Artinya, setelah N diberikan nilai-nilai Uj, tugas kami adalah menemukan parameter seperti itu, U yang memaksimalkan nilai kemungkinan. Kredibilitas (saya segera mengambil logaritma dari itu) dapat ditulis sebagai berikut:



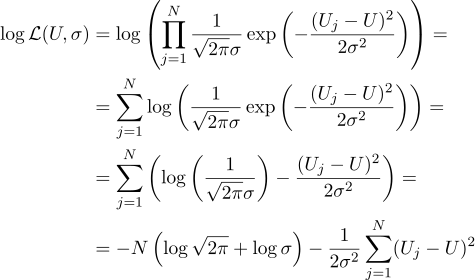
Nah, maka semuanya ketat seperti sebelumnya, kami menyamakan dengan nol derivatif parsial sehubungan dengan parameter yang kami cari:



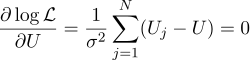
Kami menemukan bahwa perkiraan paling mungkin dari jumlah yang tidak diketahui U dapat ditemukan sebagai rata-rata dari semua pengukuran:



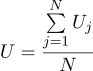
Nah, parameter sigma yang paling mungkin adalah standar deviasi biasa:




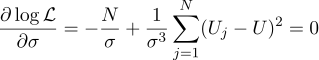
Apakah perlu repot-repot untuk mendapatkan rata-rata sederhana dari semua pengukuran dalam jawabannya? Untuk seleraku, itu sepadan. Ngomong-ngomong, rata-rata beberapa pengukuran dengan nilai konstan untuk meningkatkan akurasi pengukuran adalah praktik standar. Misalnya, rata-rata ADC . By the way, untuk kebisingan Gaussian ini tidak perlu, cukup bahwa kebisingan tidak bias.

Contoh tiga, dan sekali lagi satu dimensi

Kami melanjutkan pembicaraan, mari kita ambil contoh yang sama, tetapi sedikit rumit. Kami ingin mengukur resistansi resistor tertentu. Dengan bantuan catu daya laboratorium, kami dapat melewati sejumlah standar ampere melaluinya, dan mengukur tegangan yang akan diperlukan untuk ini. Artinya, kita akan memiliki N pasangan angka (Ij, Uj) di masukan evaluator resistensi kami.



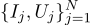
Gambarlah poin-poin ini pada grafik; Hukum Ohm memberi tahu kita bahwa kita mencari kemiringan garis biru.



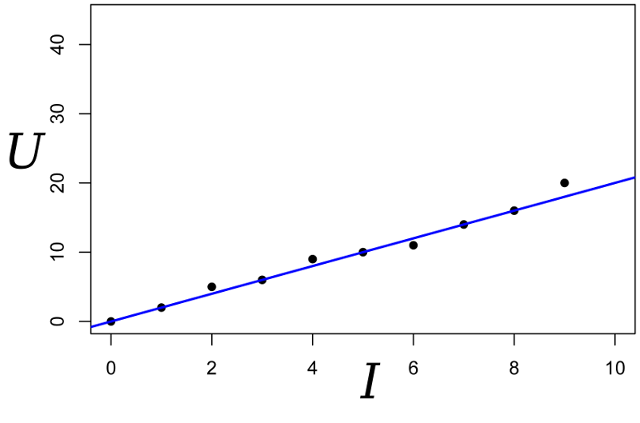
Kami menulis ekspresi untuk kemungkinan parameter R:



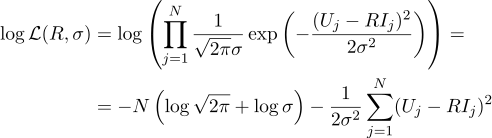
Dan lagi, kami menyamakan dengan nol turunan parsial yang sesuai:



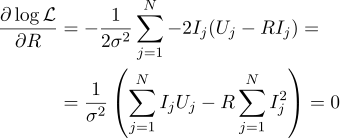
Maka resistensi R yang paling masuk akal dapat ditemukan dengan rumus berikut:



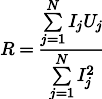
Hasil ini sudah agak kurang jelas daripada rata-rata sederhana dari semua pengukuran. Harap perhatikan bahwa jika kami melakukan seratus pengukuran di wilayah satu ampere, dan satu pengukuran di wilayah satu kilo ampere, maka seratus pengukuran sebelumnya praktis tidak akan mempengaruhi hasilnya. Mari kita ingat fakta ini, ini akan berguna bagi kita di artikel selanjutnya.

Contoh Keempat: Kembali ke Kotak Terkecil

Tentunya Anda telah memperhatikan bahwa dalam dua contoh terakhir, memaksimalkan logaritma kemungkinan sama dengan meminimalkan jumlah kuadrat dari kesalahan estimasi. Mari kita lihat contoh lain. Ambil kalibrasi steelyard menggunakan bobot referensi. Misalkan kita memiliki banyak referensi N dari massa xj, menggantungnya di atas batang baja dan mengukur panjang pegas, kita mendapatkan N panjang pegas yj:



Hukum Hooke memberi tahu kita bahwa perpanjangan pegas secara linear tergantung pada gaya yang diterapkan, dan gaya ini mencakup berat barang dan berat pegas itu sendiri. Biarkan kekakuan pegas menjadi parameter a , tetapi tegangan pegas di bawah bobotnya sendiri adalah parameter b. Kemudian kita dapat menulis ekspresi kemungkinan pengukuran kita dengan cara ini (seperti sebelumnya, di bawah hipotesis kebisingan pengukuran Gaussian):



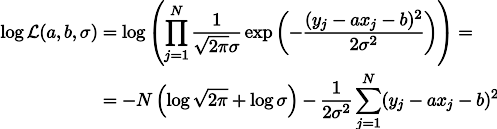
Kemungkinan maksimalisasi L setara dengan meminimalkan jumlah kuadrat dari kesalahan estimasi, yaitu, kita dapat mencari minimum fungsi S yang didefinisikan sebagai berikut:



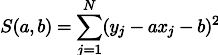
Dengan kata lain, kami mencari garis lurus yang meminimalkan jumlah kuadrat dari panjang segmen hijau:



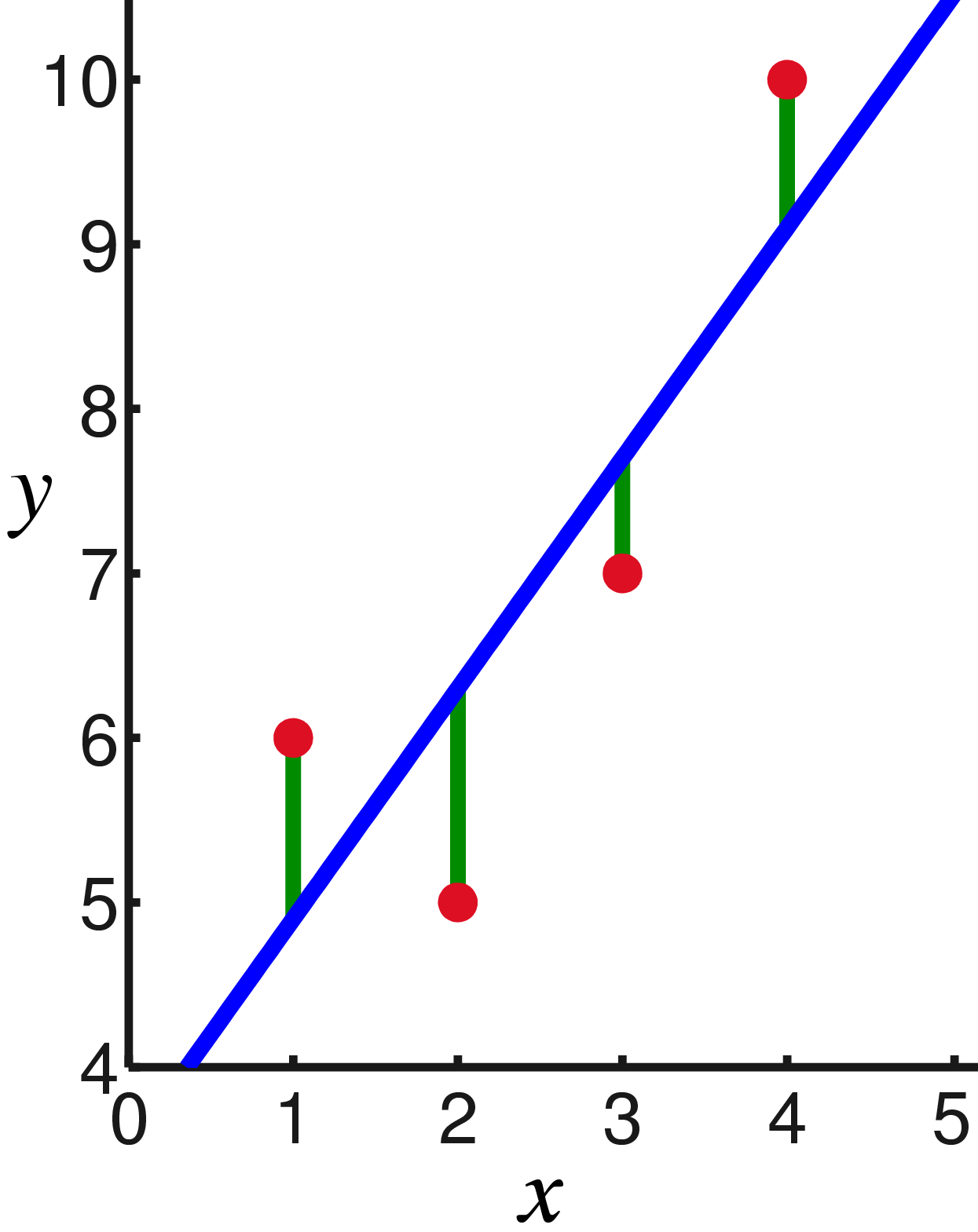
Nah, maka tidak ada kejutan, kami menetapkan turunan parsial ke nol:



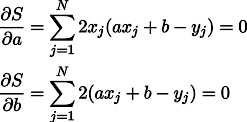
Kami mendapatkan sistem dua persamaan linear dengan dua tidak diketahui:



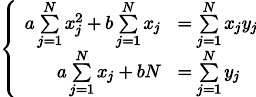
Kami mengingat kelas tujuh sekolah dan menulis solusinya:

Kesimpulan

Metode kuadrat terkecil adalah kasus khusus memaksimalkan kemungkinan untuk kasus-kasus di mana kepadatan probabilitas adalah Gaussian. Dalam kasus ketika kepadatan adalah (tidak sama sekali) Gaussian, kuadrat terkecil memberikan estimasi yang berbeda dari MLE (estimasi likehood maksimum). Ngomong-ngomong, pada suatu waktu, Gauss berhipotesis bahwa distribusi tidak berperan, hanya independensi tes yang penting.

Seperti yang Anda lihat dari artikel ini, semakin jauh ke dalam hutan, semakin rumit solusi analitis untuk masalah ini. Ya, kita tidak berada di abad kedelapan belas, kita memiliki komputer! Lain kali kita akan melihat geometris dan, kemudian, pendekatan terprogram untuk masalah OLS, tetap di telepon.