Saya bersiap untuk waktu yang lama dan mengumpulkan materi, saya harap kali ini ternyata lebih baik. Saya mencurahkan artikel ini untuk metode dasar untuk menyelesaikan masalah pengoptimalan matematis dengan batasan, jadi jika Anda mendengar bahwa metode simpleks adalah beberapa metode yang
sangat penting , tetapi masih tidak tahu apa fungsinya, maka artikel ini mungkin akan membantu Anda.
PS Artikel ini berisi rumus matematika yang ditambahkan oleh editor makro. Mereka mengatakan bahwa kadang-kadang mereka tidak ditampilkan. Ada juga banyak animasi dalam format gif.
Pembukaan
Masalah optimasi matematis adalah masalah bentuk “Cari di set
mathcalK elemen
x∗ sedemikian rupa untuk semua
x dari
mathcalK dilakukan
f(x∗) leqf(x) ", Yang dalam literatur ilmiah kemungkinan akan dituliskan seperti ini
\ begin {array} {rl} \ mbox {minim} & f (x) \\ \ mbox {disediakan} & x \ in \ mathcal {K}. \ end {array}
\ begin {array} {rl} \ mbox {minim} & f (x) \\ \ mbox {disediakan} & x \ in \ mathcal {K}. \ end {array}
Secara historis, metode populer seperti gradient descent atau metode Newton hanya bekerja di ruang linear (dan lebih disukai yang sederhana, misalnya
mathbbRn ) Dalam praktiknya, seringkali ada masalah di mana Anda perlu menemukan minimum bukan di ruang linear. Misalnya, Anda perlu menemukan minimum beberapa fungsi pada vektor tersebut
x=(x1, ldots,xn) untuk itu
xi geq0 , ini mungkin karena fakta bahwa
xi menunjukkan panjang benda apa pun. Atau misalnya, jika
x mewakili koordinat titik yang seharusnya tidak lebih dari
r dari
y yaitu
|x−y | leqr . Untuk masalah seperti itu, gradient descent atau metode Newton tidak lagi dapat diterapkan secara langsung. Ternyata kelas yang sangat besar dari masalah optimasi mudah dijangkau oleh "pembatasan", mirip dengan yang saya jelaskan di atas. Dengan kata lain, lebih mudah untuk mewakili set
mathcalK dalam bentuk sistem persamaan dan ketidaksetaraan
beginarraylgi(x) leq0, 1 leqi leqm,hi(x)=0, 1 leqi leqk. endarray
Minimisasi masalah pada ruang formulir
mathbbRn dengan demikian mereka mulai secara sewenang-wenang menyebut mereka "masalah yang tidak dibatasi", dan masalah atas perangkat yang didefinisikan oleh set persamaan dan ketidaksetaraan - "masalah terbatas".
Secara teknis, benar-benar banyak orang
mathcalK dapat direpresentasikan sebagai persamaan tunggal atau ketidaksetaraan menggunakan fungsi-
indikator , yang didefinisikan sebagai
I_ \ mathcal {K} (x) = \ begin {case} 0, & x \ notin \ mathcal {K} \\ 1, & x \ in \ mathcal {K}, \ end {cases}
I_ \ mathcal {K} (x) = \ begin {case} 0, & x \ notin \ mathcal {K} \\ 1, & x \ in \ mathcal {K}, \ end {cases}
Namun, fungsi seperti itu tidak memiliki berbagai sifat yang berguna (konveksitas, diferensiabilitas, dll.). Namun, orang sering bisa membayangkan
mathcalK dalam bentuk beberapa persamaan dan ketidaksetaraan, masing-masing memiliki sifat tersebut. Teori dasar dirangkum dalam kasus ini
\ begin {array} {rl} \ mbox {minimal} & f (x) \\ \ mbox {disediakan} & g_i (x) \ leq 0, ~ 1 \ leq i \ leq m \\ & Ax = b , \ end {array}
\ begin {array} {rl} \ mbox {minimal} & f (x) \\ \ mbox {disediakan} & g_i (x) \ leq 0, ~ 1 \ leq i \ leq m \\ & Ax = b , \ end {array}
dimana
f,gi - fungsi cembung (tetapi tidak selalu dapat dibedakan),
A - matriks. Untuk menunjukkan bagaimana metode ini bekerja, saya akan menggunakan dua contoh:
- Tugas pemrograman linier
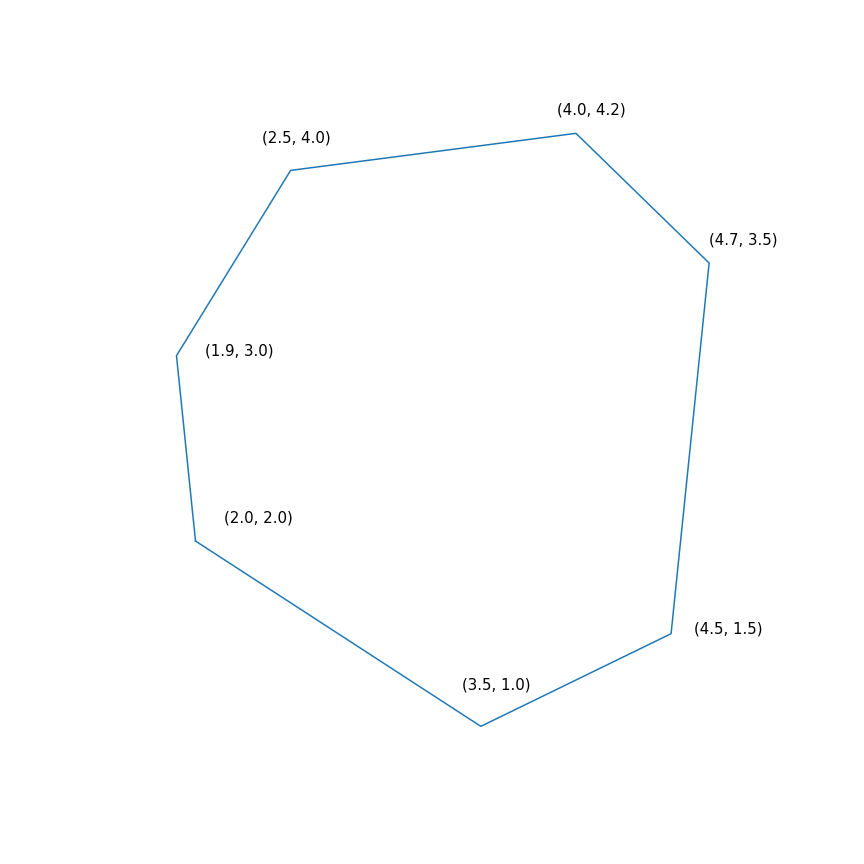
$$ menampilkan $$ \ begin {array} {rl} \ mbox {minimal} & -2 & x ~~~ - & y \\ \ mbox {disediakan} & -1.0 & ~ x -0.1 & ~ y \ leq -1.0 \ \ & -1.0 & ~ x + ~ 0.6 & ~ y \ leq -1.0 \\ & -0.2 & ~ x + ~ 1.5 & ~ y \ leq -0.2 \\ & ~ 0.7 & ~ x + ~ 0.7 & ~ y \ leq 0.7 \\ & ~ 2.0 & ~ x -0.2 & ~ y \ leq 2.0 \\ & ~ 0.5 & ~ x -1.0 & ~ y \ leq 0.5 \\ & -1.0 & ~ x -1.5 & ~ y \ leq - 1.0 \\ \ end {array} $$ menampilkan $$
Pada dasarnya, masalah ini terdiri dari menemukan titik terjauh dari poligon ke arah (2, 1), solusi untuk masalah adalah titik (4.7, 3.5) - yang paling "benar" dalam poligon). Tapi poligon itu sendiri
- Meminimalkan fungsi kuadratik dengan satu kendala kuadratik
\ begin {array} {rl} \ mbox {minimal} & 0,7 (x - y) ^ 2 + 0,1 (x + y) ^ 2 \\ \ mbox {disediakan} & (x-4) ^ 2 + ( y-6) ^ 2 \ leq 9 \ end {array}
\ begin {array} {rl} \ mbox {minimal} & 0,7 (x - y) ^ 2 + 0,1 (x + y) ^ 2 \\ \ mbox {disediakan} & (x-4) ^ 2 + ( y-6) ^ 2 \ leq 9 \ end {array}
Metode simpleks
Dari semua metode yang saya bahas dengan ulasan ini, metode simpleks mungkin yang paling terkenal. Metode ini dikembangkan secara khusus untuk pemrograman linier dan satu-satunya yang disajikan mencapai solusi tepat dalam sejumlah langkah terbatas (asalkan aritmatika yang tepat digunakan untuk perhitungan, dalam praktiknya ini biasanya tidak demikian, tetapi secara teori dimungkinkan). Gagasan metode simpleks terdiri dari dua bagian:
- Sistem ketidaksetaraan dan persamaan linear menentukan polyhedra cembung multidimensi (polytopes). Dalam kasus satu dimensi, ini adalah titik, sinar, atau segmen, dalam kasus dua dimensi, poligon cembung, dalam kasus tiga dimensi, polihedron cembung. Meminimalkan fungsi linear pada dasarnya menemukan titik "terjauh" ke arah tertentu. Saya pikir intuisi harus menyarankan bahwa titik terjauh ini harus menjadi puncak tertentu, dan memang demikian. Secara umum, untuk sistem dari m ketidaksetaraan dalam n -dimensi ruang simpul adalah titik yang memuaskan suatu sistem yang tepat n dari ketidaksetaraan ini berubah menjadi persamaan (asalkan di antara ketidaksetaraan tidak ada yang setara). Selalu ada jumlah terbatas dari poin-poin seperti itu, walaupun jumlahnya bisa banyak.
- Sekarang kita memiliki serangkaian poin yang terbatas, secara umum, Anda dapat memilih dan memilahnya, yaitu, lakukan sesuatu seperti ini: untuk setiap subset dari n ketidaksetaraan, selesaikan sistem persamaan linear yang disusun berdasarkan ketidaksetaraan yang dipilih, verifikasi bahwa solusi tersebut cocok dengan sistem ketidaksetaraan yang asli dan bandingkan dengan poin-poin lainnya. Ini adalah metode kerja yang tidak efisien tetapi cukup sederhana. Metode simpleks, alih-alih iterasi, bergerak dari atas ke atas sepanjang tepi sehingga nilai-nilai fungsi tujuan meningkat. Ternyata jika sebuah simpul tidak memiliki "tetangga" di mana nilai-nilai fungsi lebih baik, maka itu optimal.
Metode simpleks bersifat iteratif, yaitu sedikit meningkatkan solusi. Untuk metode seperti itu, Anda harus mulai di suatu tempat, dalam kasus umum ini dilakukan dengan menyelesaikan masalah tambahan
\ begin {array} {rl} \ mbox {minimal} & s \\ \ mbox {disediakan} & g_i (x) \ leq s, ~ 1 \ leq i \ leq m \\ \ end {array}
\ begin {array} {rl} \ mbox {minimal} & s \\ \ mbox {disediakan} & g_i (x) \ leq s, ~ 1 \ leq i \ leq m \\ \ end {array}
Jika untuk mengatasi masalah ini
x∗,s∗ sedemikian rupa
s∗ leq0 kemudian dieksekusi
gi(x∗) leqs leq0 jika tidak, masalah asli biasanya diberikan pada set kosong. Untuk mengatasi masalah tambahan, Anda juga dapat menggunakan metode simpleks, tetapi titik awalnya dapat diambil
s= maxigi(x) dengan sewenang-wenang
x . Menemukan titik awal dapat secara sewenang-wenang disebut fase pertama dari metode, menemukan solusi untuk masalah awal dapat secara sewenang-wenang disebut fase kedua dari metode tersebut.
Lintasan metode simpleks dua faseLintasan dibuat menggunakan scipy.optimize.linprog.
Keturunan Gradien Proyektif
Tentang gradient descent, saya baru-baru ini menulis
artikel terpisah di mana saya juga menjelaskan metode ini secara singkat. Sekarang metode ini cukup hidup, tetapi sedang dipelajari sebagai bagian dari
penurunan gradien proksimal yang lebih umum. Gagasan metode ini cukup dangkal: jika kita menerapkan gradient descent ke fungsi cembung
f , lalu dengan pilihan parameter yang tepat kita mendapatkan minimum global
f . Jika, setelah setiap langkah penurunan gradien, titik yang diperoleh dikoreksi, sebagai gantinya mengambil proyeksi ke set cembung tertutup
mathcalK , maka sebagai hasilnya kita mendapatkan fungsi minimum
f pada
mathcalK . Nah, atau lebih formal, penurunan gradien projektif adalah algoritma yang menghitung secara berurutan
begincasesxk+1=yk− alphak nablaf(yk)yk+1=P mathcalK(xk+1), endcases
dimana
P mathcalK(x)= mboxargminy in mathcalK |x−y |.
Kesetaraan terakhir mendefinisikan operator standar proyeksi ke set, pada kenyataannya, itu adalah fungsi itu
x menghitung titik terdekat ke set
mathcalK . Peran jarak dimainkan di sini
| ldots | , perlu dicatat bahwa
norma apa pun dapat digunakan di sini, namun, proyeksi dengan norma yang berbeda mungkin berbeda!
Dalam praktiknya, penurunan gradien proyektif hanya digunakan dalam kasus khusus. Masalah utamanya adalah bahwa menghitung proyeksi bisa menjadi lebih sulit daripada yang asli, dan itu perlu dihitung berkali-kali. Kasus paling umum yang nyaman untuk menggunakan penurunan gradien projektif adalah “pembatasan kotak”, yang memiliki formulir
elli leqxi leqri, 1 leqi leqn.
Dalam hal ini, proyeksi dihitung dengan sangat sederhana, untuk setiap koordinat ternyata
[P _ {\ mathcal {K}} (x)] _ i = \ begin {cases} r_i, & x_i> r_i \\ \ ell_i, & x_i <\ ell_i \\ x_i, & x_i \ di [\ ell_i, r_i ] \ end {cases}
Penggunaan keturunan gradien proyektif untuk masalah pemrograman linier sama sekali tidak berarti, namun, jika Anda melakukan ini, itu akan terlihat seperti ini
Lintasan gradien keturunan proyektif untuk masalah pemrograman linier Dan di sini adalah lintasan dari penurunan gradien proyektif untuk masalah kedua, jika
pilih ukuran langkah besar dan jika
pilih ukuran langkah kecil Metode Ellipsoid
Metode ini patut diperhatikan karena merupakan algoritma polinomial pertama untuk masalah pemrograman linier, dapat dianggap sebagai generalisasi multidimensi dari
metode pembagian dua . Saya akan mulai dengan metode yang lebih umum
untuk memisahkan hyperplane :
- Pada setiap langkah metode, ada beberapa set yang berisi solusi untuk masalah tersebut.
- Pada setiap langkah, hyperplane dibangun, setelah itu semua titik yang terletak di satu sisi hyperplane yang dipilih dihapus dari set, dan beberapa poin baru dapat ditambahkan ke set ini
Untuk masalah optimisasi, konstruksi "hyperplane pemisah" didasarkan pada ketidaksetaraan berikut untuk fungsi cembung
f(y) geqf(x)+ nablaf(x)T(y−x).
Jika diperbaiki
x , lalu untuk fungsi cembung
f setengah ruang
nablaf(x)T(y−x) geq0 hanya berisi poin dengan nilai tidak kurang dari pada suatu titik
x , yang berarti mereka dapat terputus, karena poin-poin ini tidak lebih baik daripada yang telah kami temukan. Untuk masalah dengan batasan, Anda juga bisa menyingkirkan poin yang dijamin melanggar salah satu batasan.
Versi paling sederhana dari metode hyperplane pemisah adalah dengan hanya memotong setengah ruang tanpa menambahkan poin. Akibatnya, pada setiap langkah kita akan memiliki polyhedron tertentu. Masalah dengan metode ini adalah bahwa jumlah wajah polyhedron cenderung meningkat dari langkah ke langkah. Selain itu, ia dapat tumbuh secara eksponensial.
Metode ellipsoid sebenarnya menyimpan ellipsoid di setiap langkah. Lebih tepatnya, setelah hyperplane dibangun, ellipsoid volume minimal dibangun, yang berisi salah satu bagian dari aslinya. Ini dapat dicapai dengan menambahkan poin baru. Suatu ellipsoid selalu dapat didefinisikan dengan matriks pasti positif dan vektor (pusat ellipsoid) sebagai berikut
\ mathcal {E} (P, x) = \ {z ~ | ~ (z-x) ^ TP (z-x) \ leq 1 \}.
Konstruksi ellipsoid minimum dalam volume, yang mengandung persimpangan setengah-ruang dan ellipsoid lain, dapat dilakukan dengan menggunakan
formula yang cukup rumit . Sayangnya, dalam praktiknya, metode ini masih sebagus metode simpleks atau metode titik internal.
Tapi sebenarnya cara kerjanya
dan untuk
Metode Inside Point
Metode ini memiliki sejarah panjang pengembangan, salah satu prasyarat pertama muncul sekitar waktu yang sama ketika metode simpleks dikembangkan. Tetapi pada saat itu masih belum cukup efektif untuk digunakan dalam praktik. Kemudian pada tahun 1984,
varian dari metode ini dikembangkan secara khusus untuk pemrograman linier, yang baik dalam teori maupun dalam praktik. Selain itu, metode titik internal tidak terbatas hanya untuk pemrograman linier, tidak seperti metode simpleks, dan sekarang merupakan algoritma utama untuk masalah optimasi cembung dengan pembatasan.
Ide dasar dari metode ini adalah untuk mengganti pembatasan dengan denda dalam bentuk yang disebut
fungsi penghalang . Fungsi
F:Int mathcalK rightarrow mathbbR disebut
fungsi penghalang untuk set
mathcalK jika
F(x) rightarrow+ infty mboxatx rightarrow partial mathcalK.
Di sini
Int mathcalK - di dalam
mathcalK ,
partial mathcalK - perbatasan
mathcalK . Alih-alih masalah aslinya, diusulkan untuk menyelesaikan masalah
mboxdiperkecilolehx varphi(x,t)=tf(x)+F(x).
F dan
varphi diberikan hanya di bagian dalam
mathcalK (Faktanya, dari sinilah namanya berasal), properti penghalang memastikan hal itu
varphi setidaknya
x ada Apalagi semakin banyak
t semakin besar dampaknya
f . Dalam kondisi yang cukup masuk akal, Anda dapat mencapainya jika Anda bertujuan
t hingga tak terbatas maka minimum
varphi akan menyatu dengan solusi dari masalah aslinya.
Jika diatur
mathcalK diberikan sebagai satu set ketidaksetaraan
gi(x) leq0, 1 leqi leqm maka pilihan standar fungsi penghalang adalah
penghalang logaritmikF(x)=− summi=1 ln(−gi(x)).
Poin minimum
x∗(t) fungsi
varphi(x,t) untuk berbeda
t membentuk kurva, yang biasanya disebut
jalur pusat , metode titik dalam, seolah-olah, sedang mencoba mengikuti jalur ini. Begini tampilannya
Contoh pemrograman linier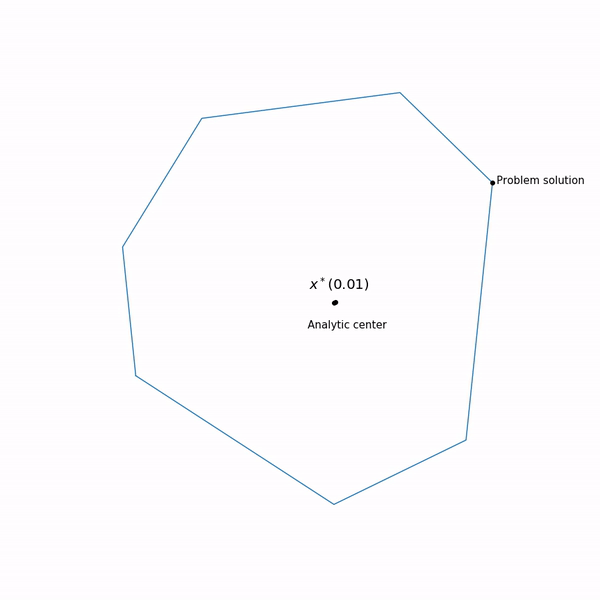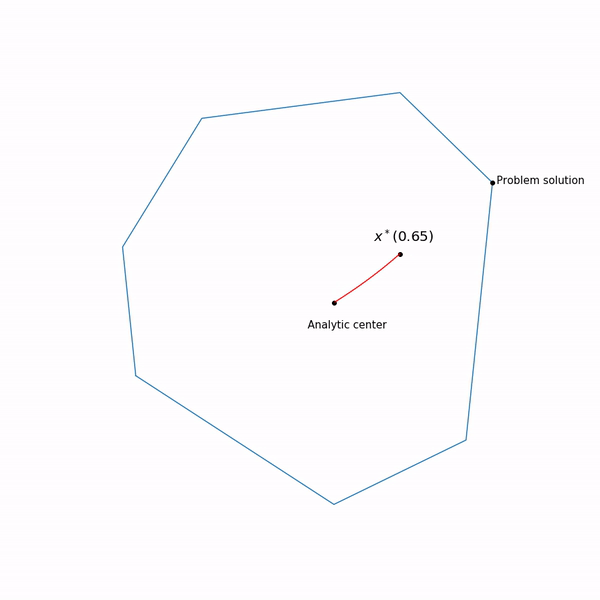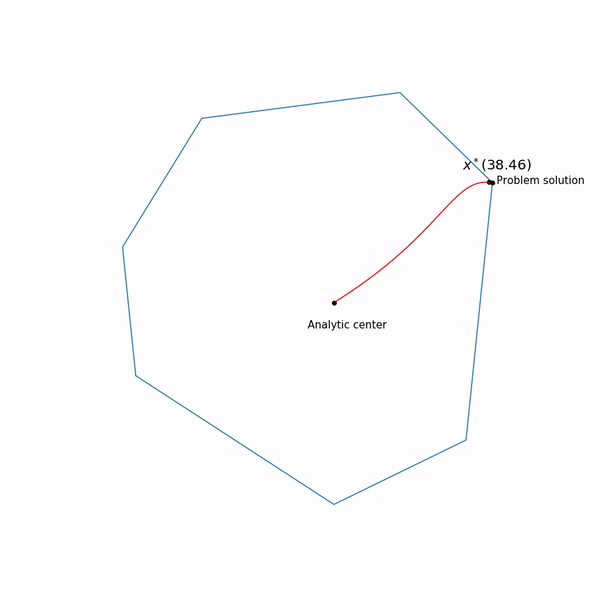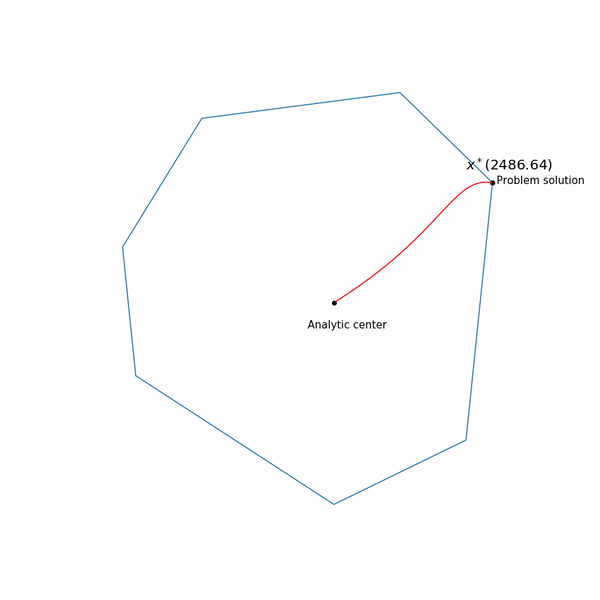 Pusat analitis
Pusat analitis adil
x∗(0) Akhirnya, metode titik internal itu sendiri memiliki bentuk berikut
- Pilih perkiraan awal x0 , t0>0
- Pilih perkiraan baru menggunakan metode Newton
xk+1=xk−[ nabla2x varphi(xk,tk)]−1 nablax varphi(xk,tk)
- Klik untuk memperbesar t
tk+1= alphatk, alpha>1
Penggunaan metode Newton di sini sangat penting: faktanya adalah bahwa dengan pilihan yang tepat dari fungsi penghalang, langkah metode Newton menghasilkan titik
yang tetap di dalam set kami , kami telah bereksperimen, tidak selalu memberikan dalam bentuk ini. Dan akhirnya, seperti inilah lintasan dari metode titik internal
Tugas pemrograman linierTitik hitam memantul adalah
x∗(tk) , yaitu titik yang kami coba untuk mendekati langkah metode Newton pada langkah saat ini.
Masalah pemrograman kuadratik